例談在變化中尋找臨界條件

朱連生

(德興一中 江西德興 334200)

臨界現象是物理中常見的現象,也是高考熱點之一.很多同學對此問題無從下手,或者知道找臨界條件,但只是靜態地停留在一個狀態(點)去研究臨界問題,而不是認真細致地研究變化的過程、以及各物理量發生變化的規律,很難發現事物發展的本來面目.

現以一道試題為例.

【試題】一彈簧一端固定在傾角為37°光滑斜面的底端,另一端拴住一質量m1=4 kg的物塊P.Q為一重物,已知Q的質量m2=8 kg.彈簧的質量不計,勁度系數k=600N/m.系統處于靜止,如圖1所示.現給Q施加一個方向沿斜面向上的力F,使它從靜止開始沿斜面向上做勻加速直線運動.已知在前0.2 s時間內,F為變力;0.2 s以后,F為恒力.求力F的最大值與最小值.(g=10m/s2)

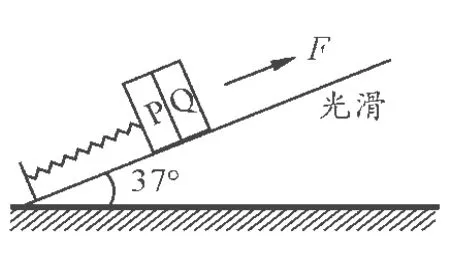
圖1

本題得分率相當低,全部做對的同學即使在重點班也是鳳毛麟角.歸納起來,主要有以下兩種錯解方式.

錯解一:以PQ整體為研究對象,由系統原先靜止時受力分析,有

當PQ一起沿斜面勻加速上滑至二者恰好脫離時,彈簧為原長,則一起上滑的位移

解得

PQ剛從斜面上一起向上勻加速運動時

P

Q剛分離時

錯解二:以PQ整體為研究對象,當系統原先靜止時受力分析,有

當PQ一起沿斜面勻加速上滑至恰好脫離時,PQ之間的壓力為零,P受力平衡,有

PQ剛從斜面上一起向上勻加速運動時

PQ剛分離時

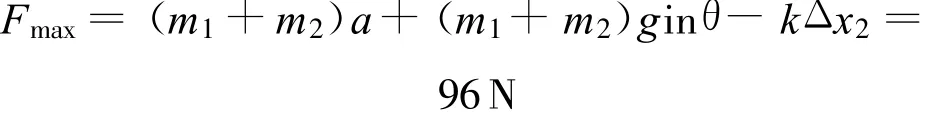
究其錯誤原因,都在于不善于找出PQ恰好脫離這一臨界狀態下所滿足的條件.解法一太武斷,想當然地認為PQ剛脫離時彈簧為原長;解法二停留在一個狀態(點)去研究臨界問題,對各物理量的變化缺乏細致地分析,認為PQ剛脫離時受力平衡,即a=0,以致于難以找到解決問題的有效方法.

臨界現象在物理中常見.當物體由一種物理狀態變為另一種物理狀態,存在一個過渡的轉折點,這時所處的狀態通常稱為臨界狀態,與之相關的物理條件則稱之為臨界條件.題干中常用“恰好”“最大”“至少”“不相撞”“不脫離”等詞語對臨界狀態給出了明確的暗示.審題時,一定要抓住這些特定的詞語,發掘其內在規律,找出臨界條件.然而,臨界條件通常具有一定的隱蔽性,靈活性較大.那么如何求解臨界問題呢?反思之余,下面結合筆者在教學工作中的一點心得體會與大家共同交流、探討.

解決臨界問題,最重要的是要抓住臨界問題的臨界條件,必須細致分析各物理量的變化情況,在變化中去研究,即不能停留在一個狀態(點)去研究臨界問題,而是要研究變化的過程、變化的各物理量,尋找臨界條件,具體基本思路如下.

1 認真審題,聯想物理情境,弄清問題中物理過程變化的細節

審題時,應力圖還原該題的物理情境,弄清物理過程的細節,分析整個過程中有幾個階段,在一些變化的過程中,物理量之間的對應關系如何發生變化.比如,物體所處的平衡狀態的破壞,物體運動方向的改變,繩子的斷裂,某物體跟另一物體相脫離或相對滑動,圓周運動物體通過最高點,帶電粒子通過電場或磁場的邊界,光線從光密介質射入光疏介質時折射角等于90°等,往往會出現臨界狀態,這就要求我們作認真細致地分析.

【例1】如圖2所示,在勻速轉動的水平圓盤上,沿半徑方向放置兩個用細線相連的質量均為m的小物體A、B,它們到轉軸的距離分別為rA=20 cm,rB=30 cm.A、B與盤面間最大靜摩擦力均為重力的0.4.試求:

(1)當細線上開始出現張力時,圓盤的角速度ω0.

(2)當A開始滑動時,圓盤的角速度ω.

(3)當A即將滑動時,燒斷細線,A、B運動狀態如何?(g取10m/s2)

圖2

分析:很多同學對于本題束手無策.然而通過研究各物理量的動態變化過程,不難發現,最初圓盤轉動角速度較小,A、B隨著圓盤做圓周運動所需的向心力較小,可由A、B與盤面間靜摩擦力提供.由于rB>rA,由公式F=mω2r可知,B所需向心力較大;當B與盤面間靜摩擦力達到最大值時(此時A與盤面間靜摩擦力還沒有達到最大),若繼續增大轉速,則B將做離心運動,從而拉緊細線,使細線上出現張力,轉速越大,細線上張力越大,使得A與盤面間靜摩擦力增大.當A與盤面間靜摩擦力也達到最大時,A將開始滑動.概括地講,本題中A、B間若沒有細繩連接,則當轉速增大到B可開始滑動時,A并不滑動,這時A、B間距離增大;若A、B間有繩連接,當B即將滑動(Ff達到Ffm)時繩才有張力,且之后直到A即將滑動前,B所受的摩擦力都為最大靜摩擦力.

解:

(1)對B

代入數據得

(2)分析A開始滑動時,A、B受力情況如圖3所示,根據牛頓第二定律

對A

對B

其中

聯立式(2)、(3)(4)解得

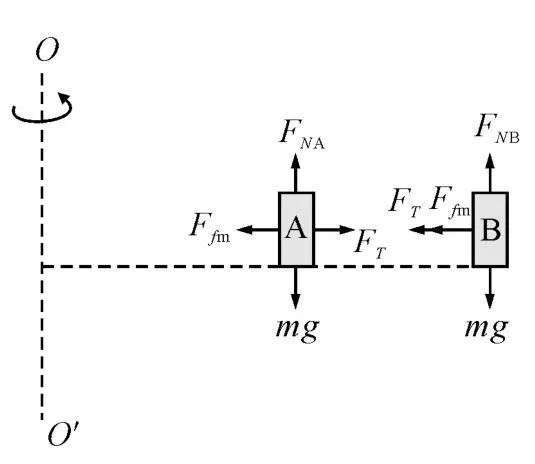
圖3

(3)燒斷細線,FT消失,A與盤面間靜摩擦力足以提供向心力使A繼續隨圓盤做圓周運動,而B由于Ffm不足以提供向心力而做離心運動.

2 尋找過程中變化的物理量,探求各物理量的變化規律

某一過程中,涉及的物理量主要是力、加速度、速度、位移等.在分析此類問題的時候,主要抓住力的變化,因為力是決定物體運動的主要因素.要著重分析力的大小變化規律、方向變化規律、受力數目的變化、力的性質的變化(如靜摩擦力轉化為滑動摩擦力)等;同時還要兼顧加速度、速度、位移等的變化情況.這些變化往往蘊含著臨界狀態的出現,此時有利于我們找到臨界條件.

【例2】一塊木板靜止在光滑水平面上,木板質量M=4 kg,小滑塊m=1 kg,小滑塊在木板的右端,它與木板的動摩擦因數μ=0.4,g=10m/s2,如果用一個水平向右的力作用在木板M上,則

(1)滑塊與木板發生相對運動的力F至少要多大?

(2)如果F=5N時,滑塊的加速度是由4N的摩擦力提供,而木板的加速度是F-f=1N的合力來提供,這樣不是滑塊的加速度大于木板的加速度嗎?這樣不是會使滑塊在右端滑落嗎?可事實上這是不可能的,為什么?

解析:隨著作用在木板的水平外力的增大,系統的加速度增大,滑塊僅依靠靜摩擦力產生加速度,直到靜摩擦力達到最大靜摩擦力,此時能產生的最大加速度是多大,這個加速度就是相對滑動的臨界加速度.本例中,力F作用在木板上,則小滑塊僅受靜摩擦力能產生的最大加速度是μg=4m/s2.因此使小滑塊相對木板滑動的最小拉力 μg(m+M)=20 N.若拉力F<20N,則小滑塊相對木板靜止,僅依靠靜摩擦力產生加速度;若F>20N,則小滑塊相對木板滑動.

3 確定臨界狀態,分析臨界條件

顯然,分析變化過程,確定物理量變化的規律,是解決問題的關鍵,從而確定臨界狀態,挖掘隱含的臨界條件,利用已學的物理規律表達各物理量之間的關系.當然要求解臨界問題,還經常涉及到一些極值問題,往往伴隨不等式的應用,自然而然也就會牽涉到一些與之相關的數學知識:三角函數、定積求和、定和求積、二次方程判別式等.

由此,對文章伊始提出的考試題,若在變化的過程中,分析臨界條件,可知PQ剛要脫離時PQ之間的壓力為零,但a不為零,因為此前一直沿斜面勻加速運動.不難得到正確解答.

正確解法:以PQ整體為研究對象,對系統原先靜止時受力分析,有

當PQ一起沿斜面勻加速上滑至恰好脫離時,PQ之間的壓力為零,以P為研究對象,進行受力分析 ,可得

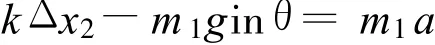
PQ剛從斜面上一起向上勻加速運動時

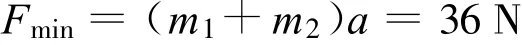
PQ剛分離時

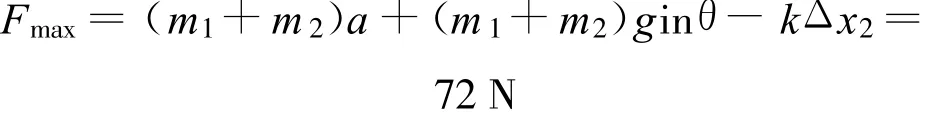
1 張傳霞.創新設計高考總復習.西安:陜西人民出版社,2007.57

2 王朝銀.步步高高考總復習.哈爾濱:黑龍江教育出版社,2009.60,77