利用分解和微元法求復場中曲線運動的最遠距離
劉月榮
(邗江中學 江蘇揚州 225009)
運動的合成與分解是研究復雜運動的重要方法.在研究比較復雜的運動時,常常采用分解的方法,將運動看作是兩個或幾個比較簡單的運動組成的,使問題容易解決.在應用分解的方法時要注意“運動的獨立性原理”.這是物體運動的一個重要特性,即一個物體同時參與幾種運動,各分運動都可看作是獨立進行的,它們互不影響.
“微元法”是分析連續過程積累的一種分析方法,其精髓就是把確定的研究對象分割為無限多個無限小的部分,然后抽取其中一部分加以研究,從而認識整體或全過程的性質和規律.這實質上是“從復合到單一,從單一到復合”的分析與綜合思維方法.
在高三專題復習中常遇到復合場中的最遠距離的求解,即可利用分解的方法和微元法來加以分析.
【例1】如圖1所示,在空間有相互垂直的勻強電場E和勻強磁場B,一電子從原點釋放,求電子在y軸方向前進的最大距離.(不計電子重力,已知電子電荷為e,質量為m)

圖1
分析:對電子在任一位置的受力進行分析,電子受到豎直向上的電場力eE及與速度垂直的洛倫茲力Bev.將電子的速度分解為水平方向的速度vx和豎直方向的速度vy,同時將洛倫茲力也分解為水平方向的作用力和豎直方向的作用力.而水平方向的洛倫茲力是由于豎直方向的速度產生的,豎直方向的洛倫茲力是由于水平方向的速度產生的,因此水平方向的洛倫茲力為Bevy,而豎直方向的洛倫茲力為Bevx(圖2).
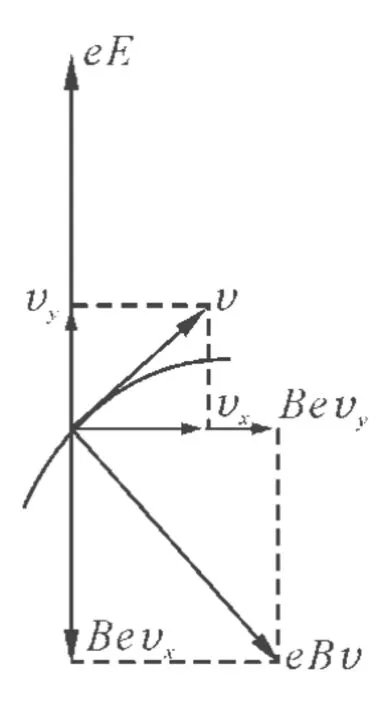
圖2
由牛頓第二定律得

設電子到達最高點時的速度為v,即

全過程中只有電場力做功,根據動能定理得

【例2】在地面上方某處的真空室里存在著水平方向的勻強電場,以水平向右和豎直向上為x軸和y軸建立直角平面坐標系.一質量為m、帶電荷為+q的微粒從點由靜止釋放后沿直線 PQ運動(圖3).當微粒到達Q(0,-l)的瞬間,撤去電場,同時加上一個垂直于紙面向外的勻強磁場(圖3中未畫),磁感應強度的大小,該磁場有理想的下邊界,其他方向范圍無限大.已知重力加速度為g.求:
(1)勻強電場的大小;
(2)撤去電場加上磁場的瞬間,粒子所受合外力的大小和方向;
(3)欲使微粒不從磁場下邊界穿出,該磁場下邊界的y軸坐標應滿足的條件.

圖3
分析:(1)微粒沿PQ直線運動時受水平向左的電場力和豎直向下的重力作用,合力沿PQ方向.因此
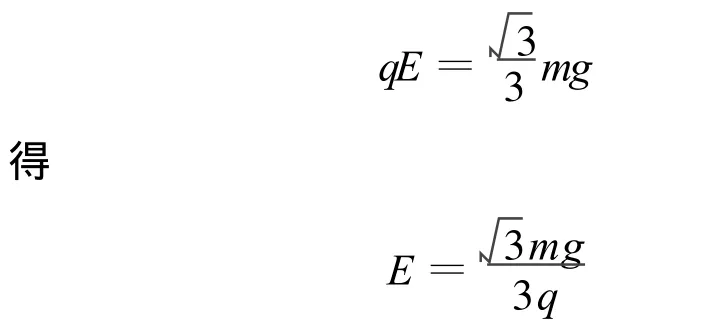
(2)撤去電場,加上磁場的瞬間,粒子在豎直方向的速度為

當微粒運動到任一點時,將微粒的速度分解為水平方向的vx和豎直方向的vy,同時將洛倫茲力也分解為水平方向的作用力和豎直方向的作用力.而水平方向的洛倫茲力是由于豎直方向的速度產生的,故為Bqvy;豎直方向的洛倫茲力是由于水平方向的速度產生的,故為 Bqvx(圖4).于是有
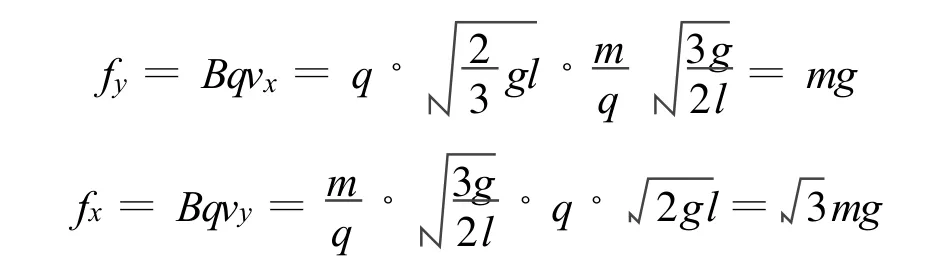
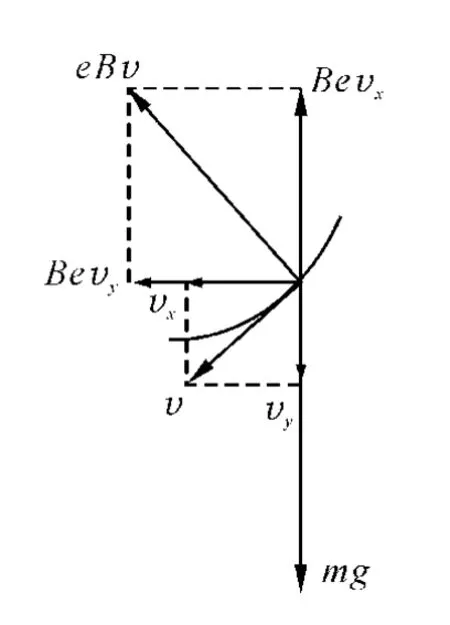
圖4
(3)撤去電場,加上磁場后,微粒做曲線運動.由牛頓第二定律得
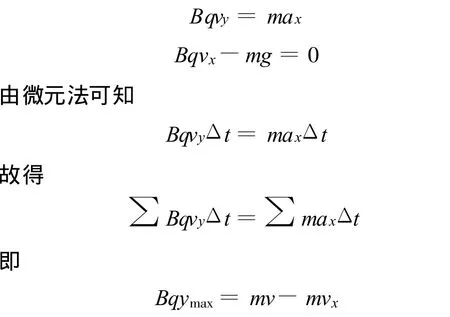
其中v為微粒運動到磁場最遠點的速度,vx為Q點的水平速度

以上是帶電粒子在復合場中做曲線運動的典型例題.對于曲線運動,一般采用分解的方法處理問題;而利用運動的分解和微元法求曲線運動中的最遠距離,正是這種題型中的亮點,也能考查學生的獨創能力.

