用“幾何畫板”的函數功能研究物理疑難問題

何征宇

(武進高級中學 江蘇常州 213161)

“幾何畫板”在物理教學中的應用已經得到了廣大物理教師的認可;它不僅能演示現象,還能夠拓展思維空間,發現“意料之外,道理之中”的問題.

筆者在高三復習教學中碰到這樣一道題:

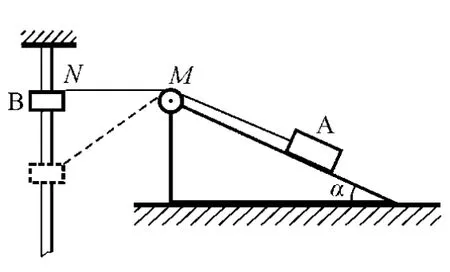
圖1

如圖1所示,一輕繩通過無摩擦的定滑輪,一端與放在傾角為α=30°的光滑斜面上的質量為m1的物體A相連,另一端與套在光滑豎直桿上質量為m2的物體B相連,定滑輪M到豎直桿的距離為l=m,桿上N點與定滑輪的高度相同,當物體B在距N點下方1m處時,A和B恰好靜止.求:

(1)物體A和B的質量之比.

(2)將物體B從N點靜止開始釋放,物體B下滑過程中的最大速度大小.

分析:對于第(1)問,根據平衡條件不難求出,物體A和B的質量之比為m1:m2=4∶1.

對于第(2)問學生在討論中出現了以下兩種觀點.

觀點1:由于物體B在N點下方1m處為平衡位置,因此,物體B經過該點時加速度為零,速度達到最大.由題目所給條件可知此時滑輪左側的繩子轉過的角度為30°.這種觀點得到了絕大部分學生支持.

觀點2:當物體B到達N點下方1m處時,受力不一定平衡,因為物體A未必處于平衡狀態,所以無法確定該點是否為B物體下滑的最大速度所在位置.這種觀點只有很少幾個學生贊同.

那么,到底兩種觀點誰是誰非呢?

分析:設物體下落時左側繩子與水平方向夾角為θ,將B物體的速度v分解為沿繩子方向的分速度v1和垂直繩子方向的分速度v2(圖2),則有

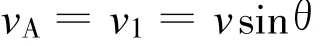
當B物體向下運動時 θ增大,可知即使B物體的速度v保持不變,A物體的速度vA也會隨θ的增大而增大.

圖2

假如觀點1成立,即B物體在N點下方1m處受力平衡,速度最大,那么在B達到最大速度時的極短時間內,其運動可以看作是勻速運動,根據以上關系式可得,A物此時處于加速狀態,繩中張力應該大于B物靜止在該點時繩中的張力,即B物體在此處受力是不平衡的,這與假設矛盾.所以觀點1錯誤,觀點2成立.

但是,僅僅通過上面的定性分析仍然無法確定B物體最大速度所在位置.下面通過計算來確定這一位置.

由機械能守恒定律得

化簡后得

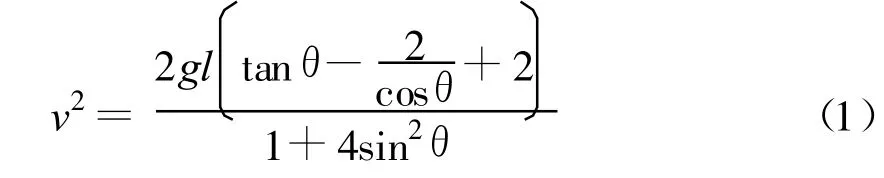
現在只需要討論(1)式中的函數的單調情況.從數學角度看,求出該函數的一階導數為零時的θ值,就能求得y的極值.但對此函數求導難度很大,而且即使求出來,也很難解出對應的 θ值.因此,想到用“幾何畫板”的函數功能進行研究.

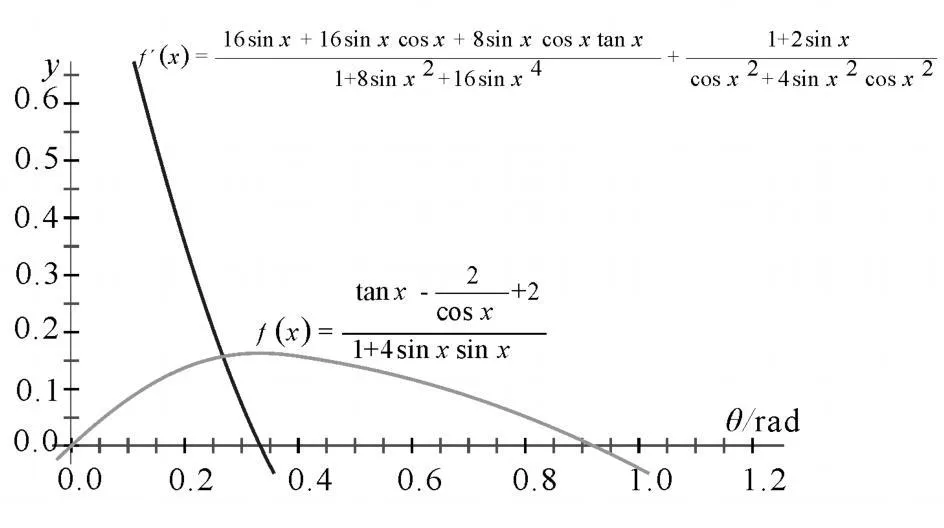
圖3

建立函數:在“幾何畫板”中選擇“圖表”菜單的“新建函數”項,輸入上面的函數(用x變量代替θ),確定后就能得到以上的函數表達式 f(x),然后選中此函數表達式,再選擇“圖表”菜單中的“導數”項,就可以由電腦完成對此函數的求導,得到導數表達式 f′(x)(圖3).但要解出 θ仍然很困難,因此,繼續采用“幾何畫板”的圖像功能來進一步研究.

繪制圖像:選中這兩個函數表達式,在“幾何畫板”中選擇“圖表”菜單的“繪制函數”,就得到了這兩個函數的圖像(圖3).

由此圖可以看出θ約為0.33rad,即θ=18.9°時B物體速度最大;并不是第一種觀點中的30°時速度最大.

體會:“幾何畫板”具有強大的計算功能和圖像功能,可以用來迅速有效地處理數據,展示物理規律,這給我們研究物理問題突破難點提供了一種有效途徑.充分利用這些功能解決常規手段難以解決的物理問題,有利于推動信息技術在物理教學中的應用.同時,也提醒我們,在編題、選題時要有科學的批判精神,要注意檢驗,用實事求是的態度對待教學,不要僅僅采取“拿來主義”.