動臂式塔機變截面吊臂的整體穩定性分析

張宏生，陸念力

(哈爾濱工業大學機電工程學院，哈爾濱150001，hszhanghit@gmail.com)

塔式起重機(簡稱塔機)廣泛應用于高層建筑施工、大型設備吊裝等諸多領域，在建筑施工中是無可替代的.動臂式塔機的吊臂通過俯仰變化來實現變幅，吊臂在吊重和變幅繩的共同作用下，近似只承受軸向壓力，因此吊臂的整體穩定性一直是設計人員關注的焦點.動臂式塔機吊臂的結構特點是由變截面的根部段、頭部段以及等截面的中間段組成的非等截面混合結構，吊臂通過根部鉸與塔身連接，變幅鋼絲繩固定在吊臂頭部.故在起升平面內，吊臂的支撐形式可簡化為簡支式，在起升平面外為懸臂式.

對于等截面柱和幾種簡單的變截面柱的穩定性，Timoshenko［1］給出精確解.為了準確地分析由變截面段和等截面段組成的非等截面混合結構穩定性，很多學者進行了研究.Rahai［2］使用修正的振動模態法和能量法研究了非等截面混合結構的穩定性.Bazeos［3］根據變截面不同變化率和不同邊界條件得到無量綱化的歐拉臨界力圖表，然后利用插值法快速計算結構的歐拉臨界力.樓夢麟［4］提出了基于Ritz展開的模態攝動法來求解變截面壓桿穩定性問題的半解析方法.在使用有限元方法進行分析時，單元剛度陣的準確性直接影響計算結果.對于等截面梁，文獻［5］從彎曲微分方程出發得到精確的Bernoulli-Euler梁單元的剛度陣.由于變截面梁的復雜性和多樣性，很多學者提出了各種變截面梁單元［6-10］，一般來說，很難獲得統一的精確剛度陣.對于階梯柱模型，文獻［11］使用等截面梁精確有限元法得到了階梯柱的遞推公式.在起重機設計規范GB/T 3811-1983中將變截面柱等效為修正計算長度的等截面柱，對于變截面段和等截面段組成的非等截面混合結構穩定性，只考慮了變截面段對稱的這一特殊情形.

本文從多節階梯柱的撓度微分方程出發，應用傳遞矩陣法，研究了簡支梁模型和懸臂梁模型這兩種支撐形式，得到多節階梯柱模型歐拉臨界力控制方程的表達式.使用各節長度相等的多節階梯柱模型模擬變截面柱，對于由變截面柱和等截面柱組成的非等截面混合結構，可統一為多節階梯柱模型.

1 多節階梯柱的傳遞矩陣法

如圖1所示的n節階梯柱模型，其中Li為第i節柱頂端到根部的長度，Ii為第i節柱的截面慣性矩，L為多節階梯柱總長，P為頂部軸力，E為彈性模量.

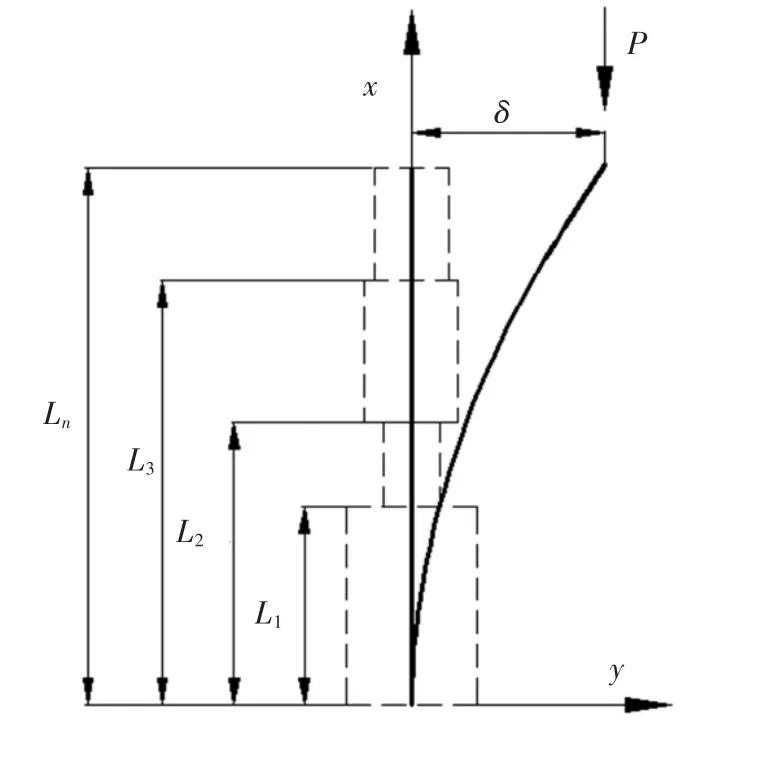
圖1 多節階梯柱模型

對于分段等截面梁模型，可列寫第i節柱的撓度微分方程為

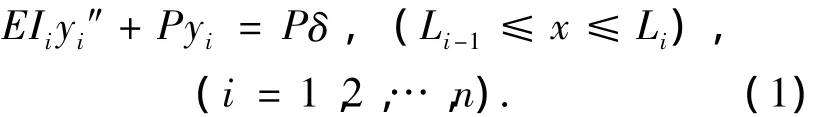
式中:L0=0，Ln=L，δ為頂部位移.

方程(1)的通解為

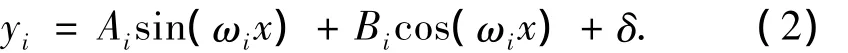
由邊界條件x=Li時，yi=yi+1且y'i=y'i+1，得到

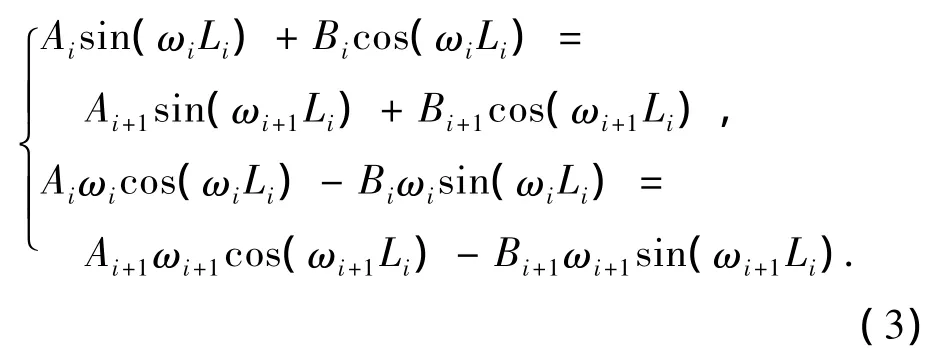
記

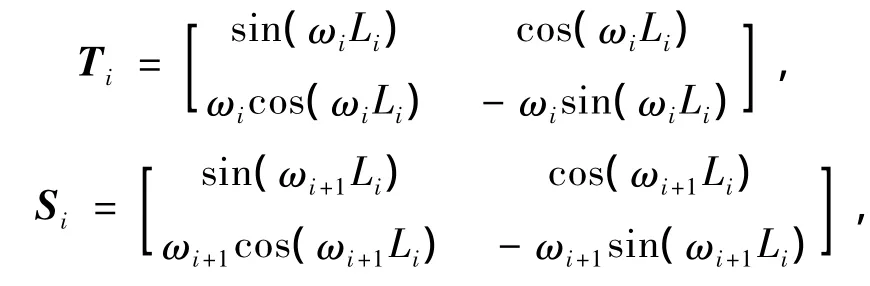
式(3)可表示為

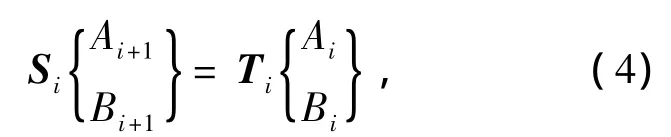
記

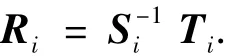
式(4)可表示為

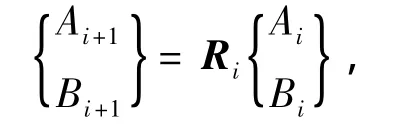
因此可得到傳遞矩陣關系為

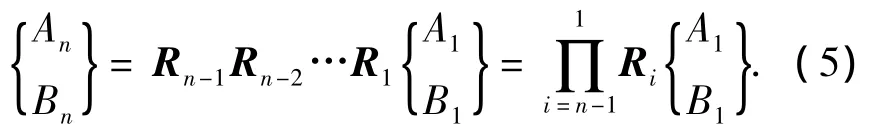
當δ=0時，式(1)和(2)即為簡支梁模型的撓度微分方程及其通解，不難證明，對于簡支梁模型的待定系數仍將滿足式(9)傳遞矩陣關系.

懸臂梁模型的根部邊界條件為y1(0)=0且y'0(0)=0，解出

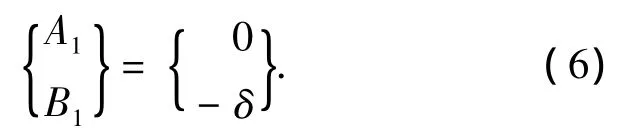
簡支梁模型的根部邊界條件為y1(0)=0，解出

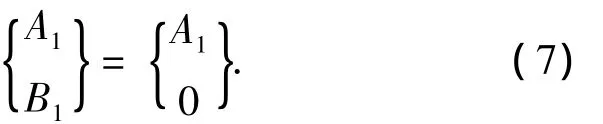
懸臂梁模型的頂部邊界條件為yn(L)=δ，簡支梁模型的頂部邊界條件為yn(L)=0，可統一表示為

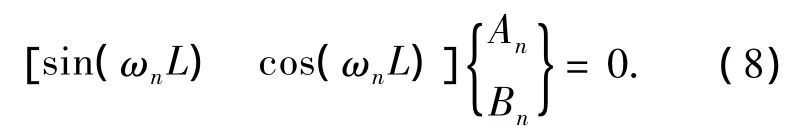
由式(8)和式(5)可獲得臨界失穩特征方程為

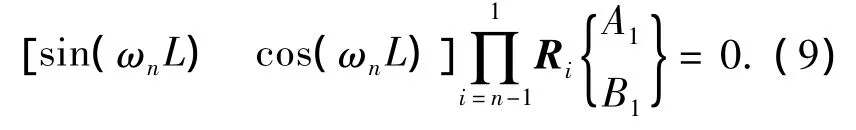
應用邊界條件(6)或(7)可分別求出懸臂梁模型或簡支梁模型的歐拉臨界力.需要指出的是，本文推導的求解多節階梯柱的歐拉臨界力的傳遞矩陣法，既沒有限制每節柱的長度，也沒有限制每節柱的截面慣性矩，也未包含任何附加假定，對多節階梯柱模型來說，本文方法得到的臨界載荷P的控制方程式(9)是精確的.

2 計算結果與比較

本文將變截面梁柱以n節長度相等的非等截面階梯柱來模擬，隨著分節數目的增多，多節階梯柱模型計算結果將趨近于精確解.對幾個經典算例進行穩定性分析，來驗證本文方法的準確性.為了便于比較，引入量綱為一的穩定系數m=PcrL2/EI2.

在計算過程中，為了簡化計算，式(6)和式(7)中可以取δ=-1和A1=1.每節階梯柱使用各節變截面兩端慣性矩的中間值，計算結果較為精確，推薦使用

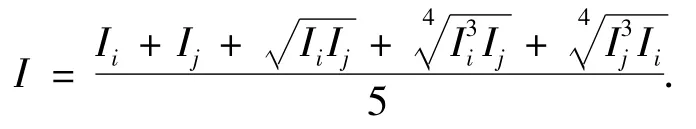
其中Ii和Ij分別為每小節變截面柱的兩端慣性矩.

例1 圖2所示為截面慣性矩為4次變化的變截面柱，a為反映截面錐度的常數，I1/I2=1/2，a/(a+L)=(1/2)1/4.圖2(a)為懸臂梁模型，其精確的歐拉臨界力［1］為Pcr=2.002EI2/L2;圖2(b)為簡支梁模型，其精確的歐拉臨界力［1］為Pcr=6.979EI2/L2，使用本文多節階梯柱的傳遞矩陣法，分成n節長度相等的非等截面階梯柱來計算歐拉臨界力，計算結果比較如表1，2所示.

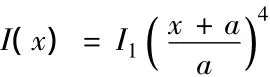
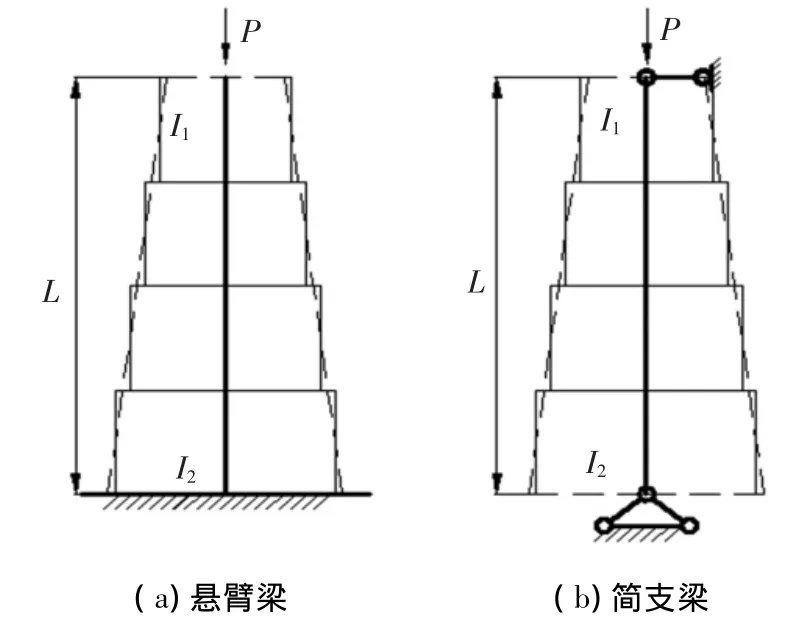
圖2 截面慣性矩按四次變化的變截面柱

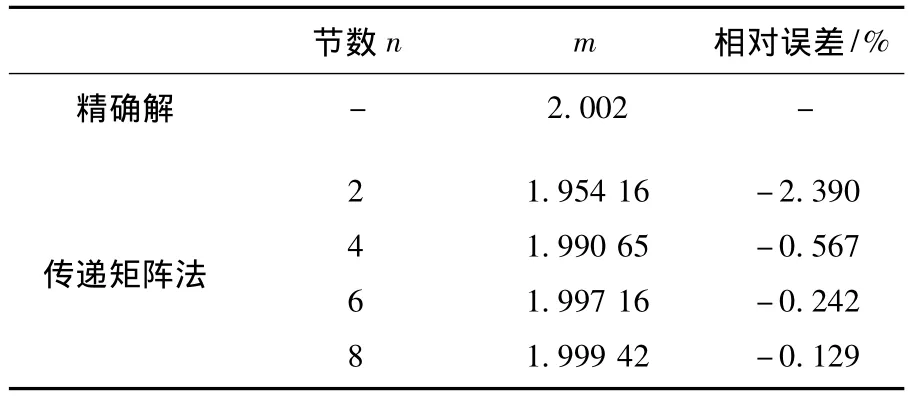
表1 截面慣性矩四次變化懸臂梁模型穩定系數m值

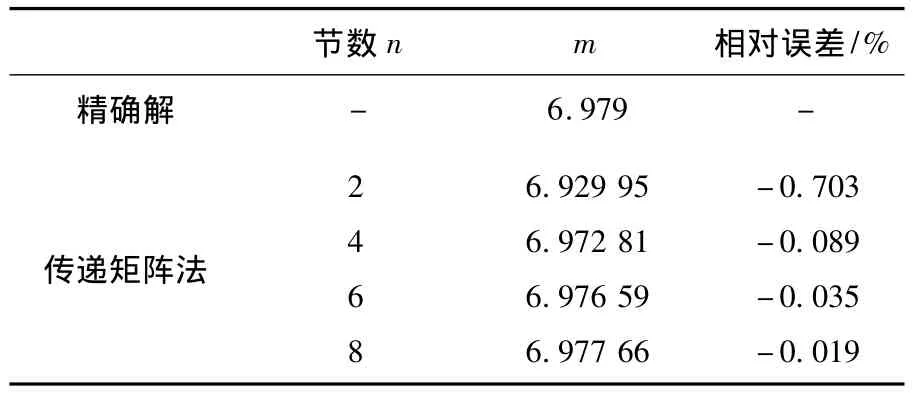
表2 截面慣性矩四次變化簡支梁模型穩定系數m值

例2 圖3所示為截面慣性矩按2次變化的變截面柱，a為反映截面錐度的常數，I1/I2= 3/10，a/(a+L)=(3/10)1/2.圖3(a)為懸臂梁模型，其精確的歐拉臨界力［1］為Pcr=1.763EI2/L2;圖3(b)為簡支梁模型，其精確的歐拉臨界力［1］為Pcr=5.622EI2/L2，使用本文多節階梯柱的傳遞矩陣法，分成n節長度相等的非等截面階梯柱來計算歐拉臨界力，計算結果比較如表3、4所示.

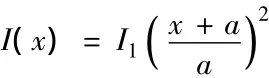
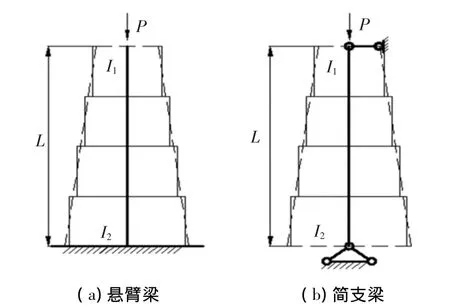
圖3 截面慣性矩按二次變化的變截面柱

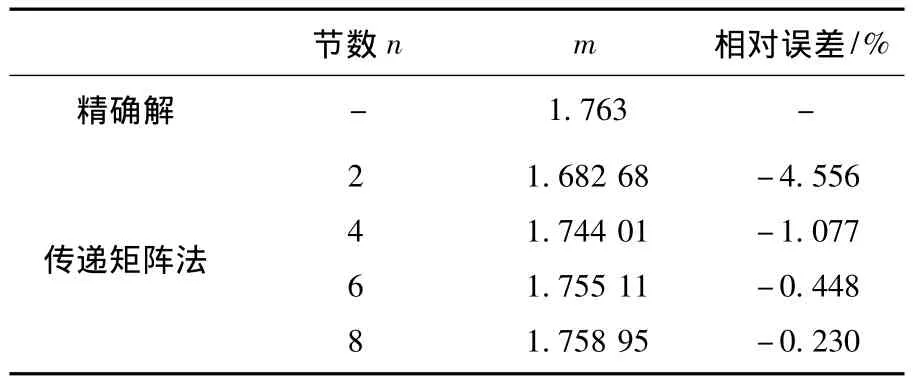
表3 截面慣性矩二次變化懸臂梁模型穩定系數m值

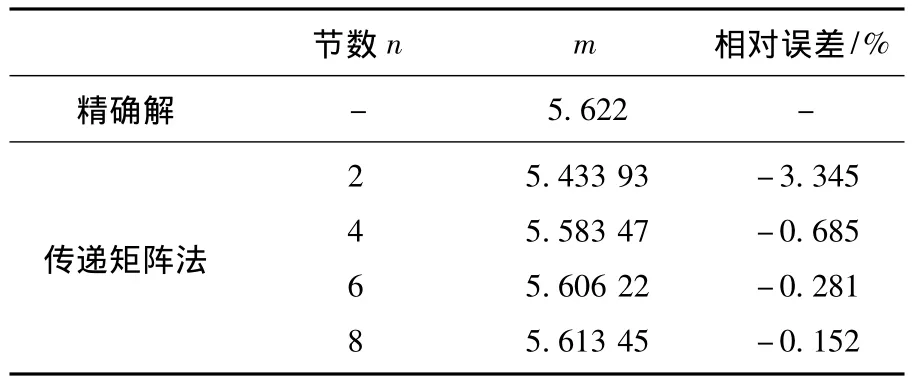
表4 截面慣性矩二次變化簡支梁模型穩定系數m值

其中表1～4的精確值來自文獻［1］，從表中可以看出，本文多節階梯柱傳遞矩陣法的計算精度很高，用6節階梯柱模擬變截面柱求解整體穩定性，將得到很好的計算結果，誤差均小于0.5%.

例3 某動臂式塔機吊臂模型如圖4所示，由a、c兩段慣性矩按2次變化的變截面段和b段等截面段組成，圖4(a)為平面內簡支式整體穩定性計算模型;圖4(b)為平面外懸臂式整體穩定性計算模型.La=0.2L，Lc=0.3L，Ia1/Ib1=0.3，Ic1/Ib1=0.4，Ib2/Ia2=0.9，Ic2/Ib2=0.4.引入無量綱穩定系數 m1= PcrL2/EIb1和 m2= PcrL2/EIa2，使用通用有限元軟件 ANSYS中的Beam44變截面梁單元，并將各段分為10～80個單元，對于平面內和平面外兩種模型，由ANSYS計算得到m值如表5所示.使用本文多節階梯柱的傳遞矩陣法，等截面段只分為1節，變截面段分為2～6節，計算結果如表6所示，其中表6中相對誤差比較的對象為使用ANSYS將每段分為80個單元得到的解.

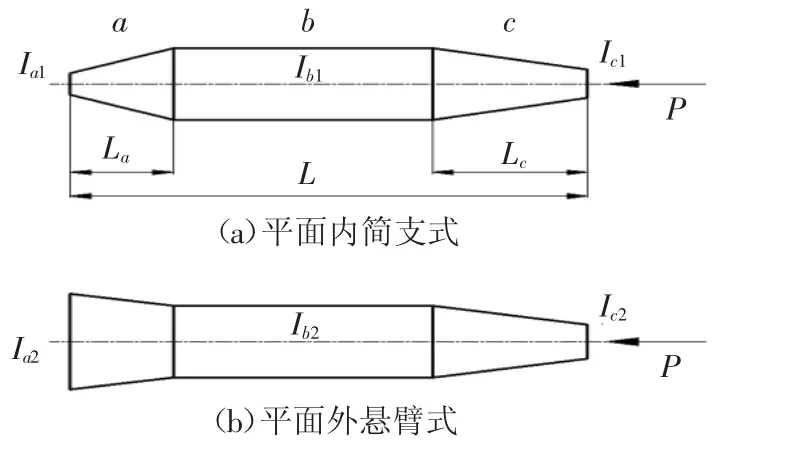
圖4 動臂式塔機吊臂模型

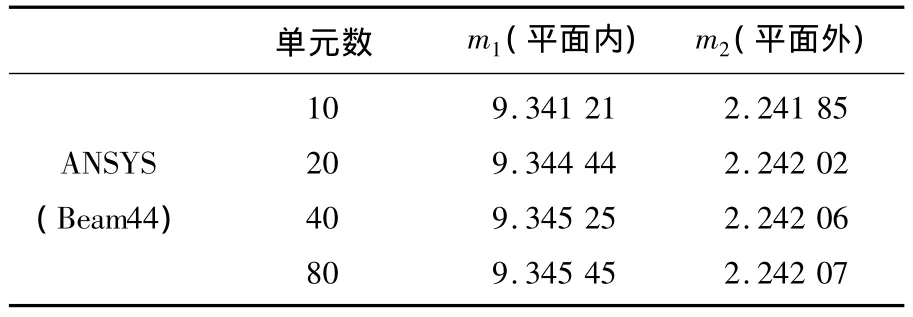
表5 動臂式塔機吊臂模型ANSYS計算穩定系數m值

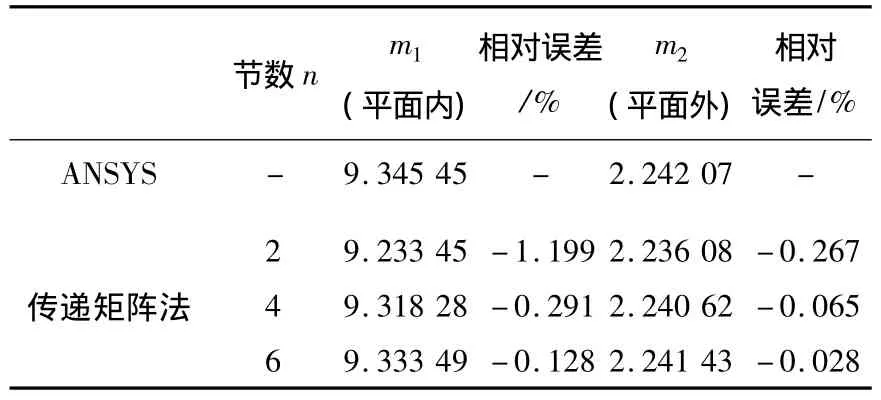
表6 動臂式塔機吊臂模型穩定系數m值

3 結論

1)本文推導的求解多節階梯柱歐拉臨界力的傳遞矩陣法，對多節階梯柱模型，該方法是精確的.當使用該方法以多節長度相等的非等截面階梯柱來模擬變截面柱，會產生誤差，但是隨著劃分節數的增多，誤差逐漸減小.

2)本文推薦將每段變截面柱劃分為6節長度相等的非等截面階梯柱，求解整體穩定性的歐拉臨界力誤差小于0.5%，精度很高.對于變截面和等截面組成的非等截面混合結構，其等截面段只需劃分為1節，變截面段劃分為6節將得到滿意的結果.

［1］TIMOSHENKO S P，GERE J M.Theory of elastic stability［M］.New York:McGraw-Hill，1961:134-141.

［2］RAHAI A R，KAZEMI S.Buckling analysis of non-prismatic columns based on modified vibration modes［J］. Communications in Nonlinear Science and Numerical Simulation，2006，13(8):1721-1735.

［3］BAZEOS N，KARABALIS D L.Efficient computation of buckling loads for plane steel frames with tapered members［J］.Enineering Structures，2006，28(5):771-775.

［4］樓夢麟，李建元.變截面壓桿穩定問題半解析解［J］.同濟大學學報，2004，32(7):857-860.

［5］陸念力，蘭朋，李良.二階理論條件下的梁桿系統精確有限元方程及應用［J］.哈爾濱建筑大學學報，1998，31(4):67-74.

［6］LI Guo-qiang，LI Jin-jun.A tapered Timoshenko-Euler beam element for analysis of steel portal frames［J］. Journal of Constructional Steel Research，2002，58: 1531-1544.

［7］BAKER G.Exact deflections in nonprismatic members［J］.Computers＆Structures，1996，61(3):515-528.

［8］郭彥林，王文明，石永久.變截面門式剛架結構的非線性性能［J］.工程力學，2000，17(4):29-36.

［9］卞敬玲，王小崗.變截面壓桿穩定計算的有限單元法［J］.武漢大學學報，2002，35(4):102-104.

［10］宋啟根，徐梁，宋丹.變截面梁柱剛度方程的Bessel函數解［J］.計算力學學報，2001，18(3):355-357.

［11］陸念力，蘭朋，白樺.起重機箱形伸縮臂穩定性分析的精確理論解［J］.哈爾濱建筑大學學報，2000，33(2):89-93.