做好兩個(gè)回歸 簡(jiǎn)化速度計(jì)算

傅賢武

(寧波市北侖區(qū)江南中學(xué) 浙江 寧波 315821)

物理概念和物理規(guī)律是嚴(yán)謹(jǐn)、科學(xué)的，同時(shí)也是理性、抽象的.在物理概念和物理規(guī)律教學(xué)時(shí)，知識(shí)的獲取主要是感知和概括.在物理習(xí)題教學(xué)時(shí)，知識(shí)的應(yīng)用主要是類比和遷移.如何讓初二學(xué)生、特別是數(shù)學(xué)基礎(chǔ)不太好的學(xué)生做好有關(guān)速度計(jì)算習(xí)題？我嘗試做好兩個(gè)回歸——回歸感性認(rèn)識(shí)和回歸形象思維，幫助學(xué)生簡(jiǎn)化速度計(jì)算.

1 從理性回歸感性——賦值法

大多數(shù)初二學(xué)生對(duì)于符號(hào)運(yùn)算和比例計(jì)算不太熟練，容易出錯(cuò).我建議他們采用賦值法，從理性的嚴(yán)謹(jǐn)計(jì)算回歸感性的驗(yàn)證計(jì)算.

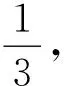
解法一：理性的嚴(yán)謹(jǐn)計(jì)算

解法二：賦值法

中間一半也就是60 m，所用時(shí)間

最后還有20 m，所用時(shí)間

所以，平均速度

【例2】三位同學(xué)的速度之比為1∶2∶3，則他們走完相同的路程所需時(shí)間之比為

A.6∶3∶2 B.3∶2∶1

C.1∶2∶3 D.2∶3∶6

解法一：理性的嚴(yán)謹(jǐn)計(jì)算

解法二：賦值法

不妨假設(shè)v1=1 m/s，v2=2 m/s，v3=3 m/s，s=6m.顯然，t1=6 s，t2=3 s，t3=2 s.當(dāng)然選A.

2 從抽象回歸形象——作圖法

一般來(lái)說(shuō)，物理計(jì)算都是在一定情景下的計(jì)算，并且這個(gè)情景大多是通過(guò)文字?jǐn)⑹霰磉_(dá)的.然而，對(duì)于很多初二學(xué)生來(lái)說(shuō)，要真正理解一大段抽象的文字所表達(dá)的情景，是有一定難度的.建議采用作圖法，從抽象的文字?jǐn)⑹龌貧w形象的物理情景.

【例3】甲和乙兩人進(jìn)行百米賽跑，他們同時(shí)出發(fā)，甲到達(dá)終點(diǎn)時(shí)，乙還剩10 m.假設(shè)他們都以原來(lái)的速度跑，將甲的起跑線向后移動(dòng)10 m，乙仍然在原來(lái)的起跑線，兩人同時(shí)出發(fā)，結(jié)果是

A.甲先到 B.乙先到

C.同時(shí)到 D.無(wú)法確定

解法一：嚴(yán)格證明，需要用不等式知識(shí)，對(duì)初二學(xué)生來(lái)講，不好理解.略.

解法二：賦值法，可以很好解決，上面已經(jīng)介紹.

亦略.

解法三：作圖法.甲和乙第一次比賽結(jié)果如圖1(a)所示.

顯然，甲的速度比乙大.

甲和乙第二次比賽過(guò)程如圖1(b)所示.

根據(jù)圖1(b)，甲到達(dá)A點(diǎn)時(shí)，乙到達(dá)B點(diǎn)，此時(shí)甲和乙距離終點(diǎn)都恰好還剩10 m路程.由于甲的速度比乙大，所以甲先到終點(diǎn).

圖1

【例4】甲乙兩人從同一座橋的同一端出發(fā)，到達(dá)另一端.甲前一半路程跑，后一半路程走；乙前一半時(shí)間跑，后一半時(shí)間走.假設(shè)甲乙走和跑的速度一樣，問(wèn)誰(shuí)先到達(dá).

解：作圖法.甲的運(yùn)動(dòng)過(guò)程如圖2(a)所示.

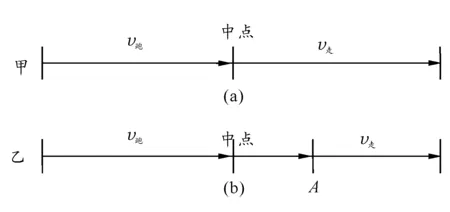
圖2

因?yàn)橐仪耙话霑r(shí)間跑，后一半時(shí)間走，所以乙要跑過(guò)中點(diǎn)，不妨假設(shè)乙跑到A點(diǎn)后開始走，且t跑=t走.則乙的運(yùn)動(dòng)過(guò)程如圖2(b)所示.

比較圖2(a)和2(b)，起點(diǎn)到中點(diǎn)那一段，甲和乙都是跑；A點(diǎn)到終點(diǎn)那一段，甲和乙都是走；他們不同之處就在于中點(diǎn)到A點(diǎn)那一段，甲是走，而乙是跑，所以乙先到.