生命線工程網絡抗震拓撲優化研究＊

李 杰,劉 威,衛書麟

(1.同濟大學土木工程學院建筑工程系,上海 200092;2.同濟大學土木工程防災國家重點試驗室,上海 200092;3.中建國際(深圳)設計顧問有限公司上海分公司,上海 200233)

0 引言

生命線工程系統是指維系現代城市與區域經濟功能的基礎性工程設施系統[1]。大多數生命線工程系統是以網絡的形式分布在城市或較大的區域范圍內,如城市的供水、供燃氣管網,區域的電力網絡等等。對生命線工程系統而言,僅僅實現各個單體的抗震性能分析以及系統的整體性能評價是遠遠不夠的,更重要的是利用這些分析工具進行網絡抗震性能的優化設計,實現以最低的造價來保證系統具有足夠的抗震性能[1]。

管網系統的抗震可靠性優化可以從提高系統單元的抗震可靠度和改進網絡的拓撲結構兩條路徑來進行。研究表明[1],綜合考慮工程實際中的各種因素,改進網絡拓撲結構要明顯優于僅僅提高單元的抗震可靠度。在管網抗震拓撲優化方面,文獻[2]利用遺傳算法初步進行了基于抗震功能可靠性的供水系統拓撲優化研究。文獻[3]則采用遺傳算法初步實現了基于連通可靠度分析的生命線管網拓撲優化。

本文首先建立了基于連通可靠度分析的生命線工程網絡抗震拓撲優化模型,介紹了應用遺傳算法到這一問題進行求解的過程,并對一個簡單燃氣管網進行了實例分析。分析表明遺傳算法用于生命線工程網絡抗震拓撲優化分析可以獲得造價低且滿足管網抗震可靠度要求的網絡。然后,改用抗震功能可靠度為約束建立了基于功能可靠度分析的供水管網的抗震拓撲優化模型,介紹了模擬退火算法來進行求解這一模型的具體過程,對一個簡單的實例分析表明應用模擬退火算法可以取得很好的效果。最后,基于功能可靠度分析的供水管網的抗震拓撲優化方法,對四川省都江堰市、綿竹市和德陽市供水管網進行了抗震拓撲優化改造分析,給出了三個城市供水管網的恢復重建方案。

1 基于連通可靠度的生命線工程網絡抗震拓撲優化

1.1 管網優化模型的建立

工程實際中,在保證安全合理的情況下,經濟性是優化改造和優化設計的主要目標。本文的管網系統優化以網絡的拓撲結構為優化對象,抗震可靠度為優化約束條件,管網建設造價為優化目標來進行。

管網系統的造價一般可以寫為:

式中:lij、dij分別為i,j節點之間的管線長度和直徑(m);γij為連通系數,鋪設該管線取1,不鋪設則取0;c(lij,dij)表示管線的造價,通常可以用下列函數來估算:

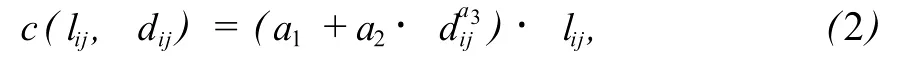
式中:a1、a2和a3都是常數,可以根據實際工程的造價采用回歸方法得到。

以管網的造價為優化目標,可以建立如下的優化模型:

式中:Pmin為管網節點的抗震連通可靠度最小值,可采用最小路遞推分解算法[4]獲得;P0為管網節點的抗震可靠度約束。

1.2 遺傳算法在抗震拓撲優化中的應用

遺傳算法是由美國科學家Holland[5]借鑒生物進化原則提出的一種自適應并行全局優化概率搜索算法。遺傳算法近年來發展迅速,在各個領域得到廣泛應用[6-7]。

下面來介紹遺傳算法應用到管網系統的拓撲結構優化問題的具體運算步驟與原理。

1.2.1 編碼

采用0～1編碼,當基因值為0時,表示該基因所對應的管線不鋪設;當基因值為1時,表示鋪設該基因對應的管線。所有優化參數對應的基因按照指定的次序排列起來,就構成一條染色體。一個染色體對應管網的一種拓撲結構方案,多條染色體構成遺傳算法的一個種群。

1.2.2 生成初始種群

采用隨機策略來生成一組個體。但是必須要注意的是,隨機生成的管網拓撲結構可能是工程中無意義的解,例如,非連通圖對應的管網結構在工程實踐中無意義。所以,在隨機生成個體之后,首先要進行管網拓撲結構的合理性判斷。對于不合理個體,進行簡單的修補;若修補后的個體仍為不合理方案,則拋棄該個體,重新生成新的個體。

1.2.3 個體評價

由于管網拓撲優化問題的優化目標是獲得滿足抗震可靠度要求的最低造價管網,而遺傳算法中一般定義適應度高的解為比較優的解,故定義染色體的適應度函數為:

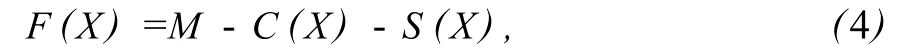
式中:M為預先指定的一個較大的數值;C(X)為個體對應管網的造價;S(X)為懲罰函數,采用下式來計算:

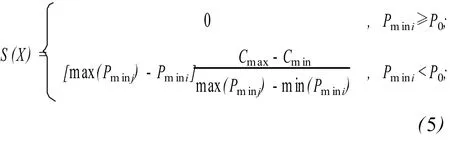
式中:Cmax、Cmin為當前群體中個體造價的最大值和最小值;Pmini為當前群體中第i個體中節點連通可靠度的最低值;j=1,2,…,N,N為當前群體中個體的數目。

1.2.4 遺傳操作

遺傳操作包括選擇、交叉和變異操作。選擇操作本文采用無放回的適應度比例方法和最佳個體保存方法。也即上一代最優的個體必然進入到下一代中,并且上一代中的每個個體按照適應度的值以一定概率遺傳到下一代中,并且只遺傳一次。交叉操作選擇一點交叉方法進行。變異操作對個體的每一個基因位,依一變異概率對其值作取反運算,從而產生一個新的個體。

1.2.5 收斂判斷

遺傳算法通常的停止規則有計算達到固定的最大進化代數,解群體間差異充分小等規則。本文采用的停止規則是計算達到固定的最大進化代數。

1.3 分析實例

圖1為10個節點,14條邊的簡單供燃氣網絡系統,源點為1,節點2～10為匯點,其管線單元屬性見表1,對于供燃氣網絡,式(2)中的a1、a2和a3可以分別取為-144.360 9,4 313.3和1.0[8],故管網的總造價為5 920萬元。

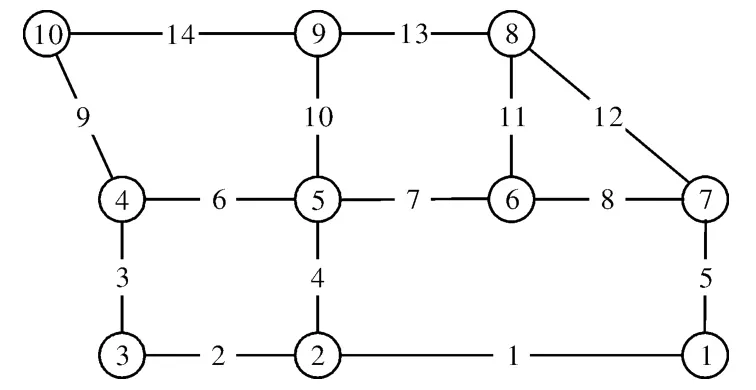
圖1 簡單燃氣管網

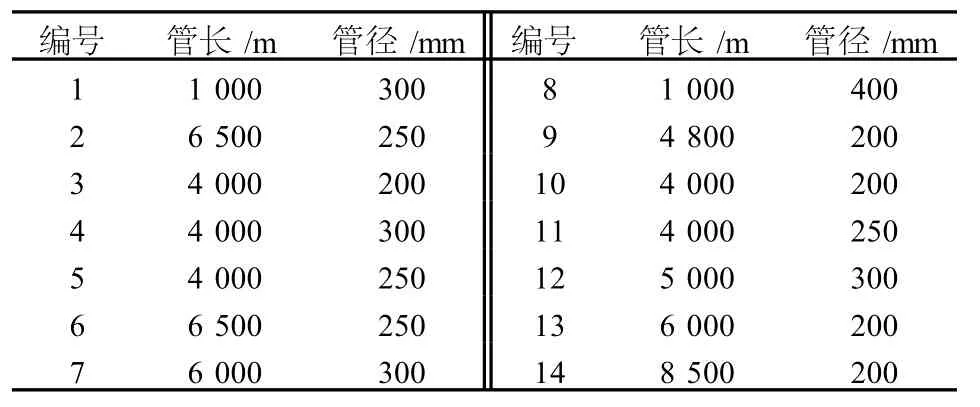
表1 管網單元屬性

假設各管線單元抗震可靠度都為0.9。設節點最低可靠度約束分別為0.7、0.8和0.9,其相應的最優網絡分別如圖2-圖4所示。采用遺傳算法對管網進行優化,算法分別計算1 000次,每次計算都是將算法從頭開始重新計算。算法搜索到上述圖2-圖4的最優結果的次數分別為622、580和808次。由此可以看出遺傳算法具有較好的搜索能力,對于上述管網,搜索到最優網絡的機會在50%以上。

圖2 可靠度約束為0.7時的最優網絡

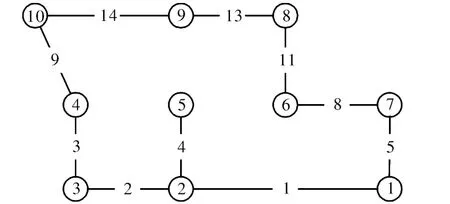
圖3 可靠度約束為0.8時的最優網絡

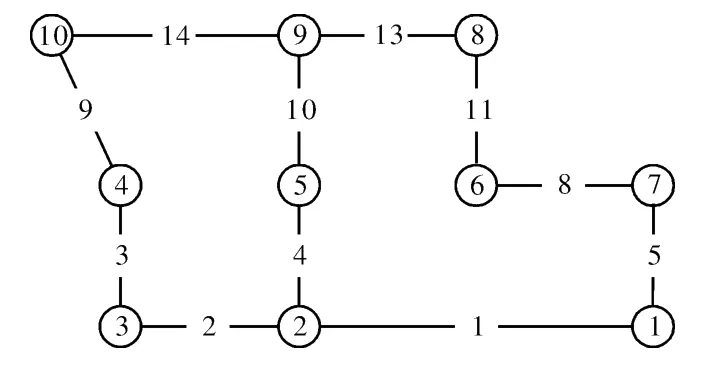
圖4 可靠度約束為0.9時的最優網絡

2 基于功能可靠度的供水管網抗震拓撲優化

2.1 供水管網優化模型

由于供水管網對于地震后社會生活和搶險救災的重要性,需要保證其在地震后的功能,也即具有足夠的供水能力來保證各種用水需求。而抗震連通可靠度只能說明從源點到用戶存在一條通路的概率,而不能保證通路能否提供足夠的水壓來滿足用戶的用水需求。因此,對于供水管網需要進行基于功能可靠度的抗震拓撲優化,以保證其在地震作用下具有足夠的供水能力。

以供水管網的造價為優化目標,可以建立如下的優化模型:

式中:βmin為供水管網所有節點的抗震可靠度指標的最小值,可以采用供水管網抗震功能可靠性分析方法[9]得到;β0為供水管網的允許抗震可靠指標限值;對于供水管網的造價,公式(2)中經驗系數a1,a2,a3可以分別取62.105 1,1 979.7,1.486[10];dmin、dmax分別為管網運行中經濟管徑的最小值和最大值。

2.2 模擬退火算法在供水網絡系統抗震拓撲優化中的應用

模擬退火的思想最早是由Metropolis[11]在1953年提出的,它源于對物體降溫過程中的統計熱力學現象的研究。Kirkpatrick等人[12]在1982年正式提出模擬退火算法,并成功地將之應用在組合優化問題中。模擬退火的基本思想是對決定性算法引入隨機擾動,使得當考察點達到局部極值時,算法過程有一個小概率“跳出”局部極值陷阱的能力。模擬退火算法是局部搜索算法的擴展,所以理論上來說,它是一個全局最優算法。

模擬退火算法用Metropolis算法產生組合優化問題解的序列,并利用下式中的Metropolis準則對應的轉移概率P確定是否接受從當前解i到新解j的轉移。

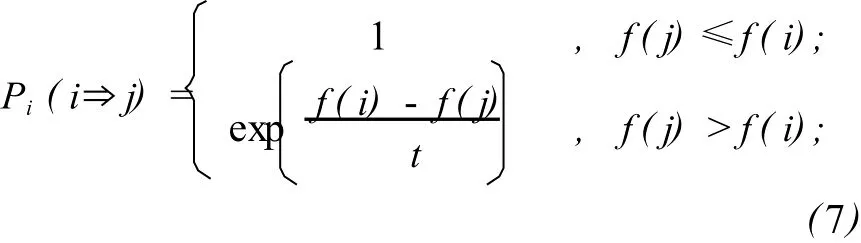
式中:f(i)為解的能量函數,這里可以取為管網的造價。

模擬退火算法從初始優化方案出發,進行降溫迭代尋找最優解。在降溫過程中,不斷地對當前管網進行隨機擾動以產生新的管網是模擬退火算法應用到供水管網抗震拓撲優化的關鍵步驟。這里,對當前管網進行隨機擾動產生新管網的操作步驟為:首先,隨機地選出一定數量的管線;然后,對選出的各管線隨機地進行狀態改變,由此得到新的管網。如果新的管網不滿足可靠度約束條件的解,采用罰函數來增大其能量函數。如果新的管網為不合理方案(如:非連通管網),這隨機增加管線來進行簡單地修補,若仍不合理則將其拋棄,重新生成一個管網。

設Lk表示Metropolis算法第k次迭代時產生的變換個數,tk表示Metropolis算法第k次迭代時控制參數t的值,T(t)表示控制參數更新函數,t0表示初始溫度,tf表示終止溫度。這模擬退火算法應用到供水管網抗震拓撲優化的具體操作步驟為:

①隨機產生一個管網作為算法初始解,以此作為當前最優點,并計算其能量函數值;

②設置初始溫度、終止溫度及控制參數更新函數:t0,tf,T(t);

③tk=T(tk-1),設置Lk,令循環計數器初值k=1;

④對當前最優點作一隨機變動,產生一個新解,計算新解的能量函數,并計算能量函數的增量Δ;

⑤若Δ＜0,則接受該新解為當前最優點;若Δ≥0,則以式(7)計算的概率接受該新解為當前最優點;

⑥若k＜Lk,則k=k+1,轉④;

⑦若t＜tf,則轉③;若t≥tf,則輸出當前最優點,算法結束;

在模擬退火算法中,溫度參數是最關鍵的參數,包括起始溫度的選取t0、溫度的下降方法T(k)和終止溫度tf的確定等。

(1)起始溫度t0的選取:采用較大的值,這里取1 000 000。

(2)溫度下降方法T(k):模擬退火算法的性能好壞主要取決于其溫度下降方法,即溫度更新函數,使其保持適當的溫度下降速度。本文采用的溫度下降方法為:tk+1=tk/k。

(3)算法的終止溫度tf,模擬退火算法從初始溫度開始,通過在每一溫度的迭代和溫度的下降,最后達到終止溫度tf而停止。本文采用零度法,即令tf為一個比較小的正數。

2.3 實例分析

圖5(a)為一個17個節點,27條邊的小型網絡,考慮Ⅷ度地震烈度背景對其進行拓撲優化設計。優化的約束條件分別為節點最低可靠度指標不得低于1.28(對應于可靠度不低于0.9),0.84(對應于可靠度不低于0.8),0.53(對應于可靠度不低于0.7)。圖5(b)、(c)、(d)分別為節點最小可靠度指標分別為1.28,0.84,0.53的供水管網最優拓撲結構布置圖。表2給出了三種約束條件下的建造費用。可以看出,節點最小可靠度指標約束值β0越大,相應的優化結構越復雜,相應的造價就越高。但不管哪種方案,相對原始方案而言,在造價上均有顯著降低。圖6為約束條件為1.28時模擬退火算法搜索過程中的點的搜索軌跡。由圖可見,模擬退火算法能很快搜索到滿足約束條件的解,并在眾多解中,選出既滿足約束條件又是造價最低的解。

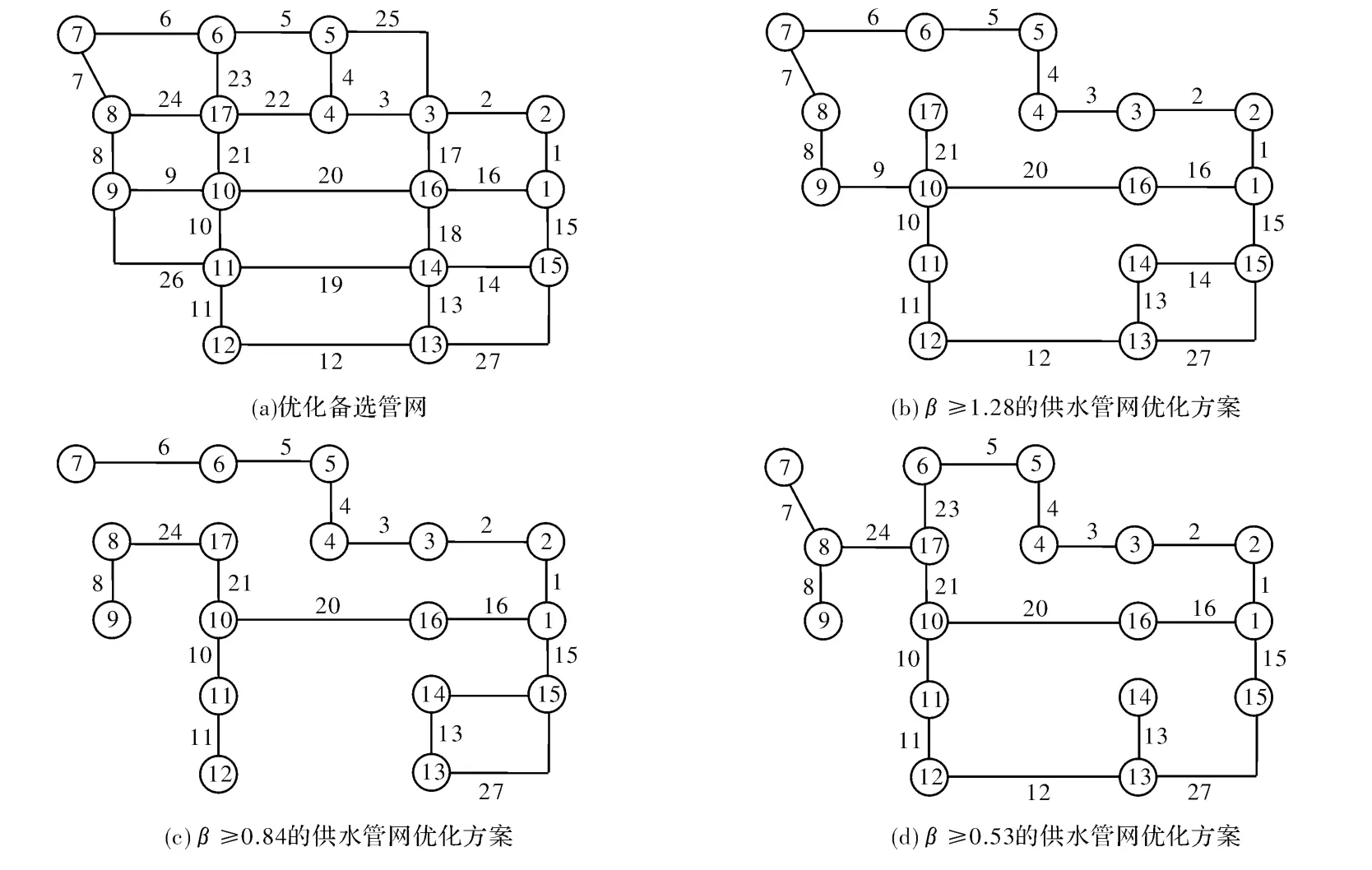
圖5 備選管網布置圖及各可靠度約束下管網拓撲結構

圖6 管網拓撲優化搜索軌跡圖

表2 各種約束條件下的系統造價

3 四川省供水管網恢復重建研究

2008年汶川大地震給四川省多個城市的供水管網造成了巨大的破壞,震后急需迅速展開恢復重建工作。在四川省建設廳、四川省給排水協會的支持和配合下,以震害調查為基礎,利用上述模擬退火算法,對一批典型受災城市的供水管網系統進行了震后恢復重建方案研究,這一研究的技術路線如圖7所示。在這一工作中,以管網節點的最低抗震功能可靠度大于0.8為約束條件進行震后供水管網系統拓撲優化分析給出了震后恢復重建方案。圖8-圖10分別為都江堰市、綿竹市和德陽市供水管網恢復重建與優化改造方案圖。

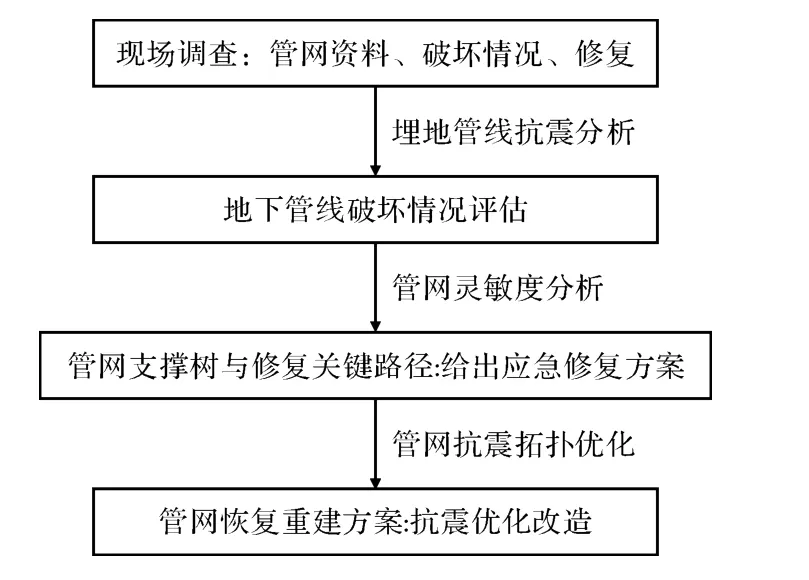
圖7 技術路線圖

4 小結

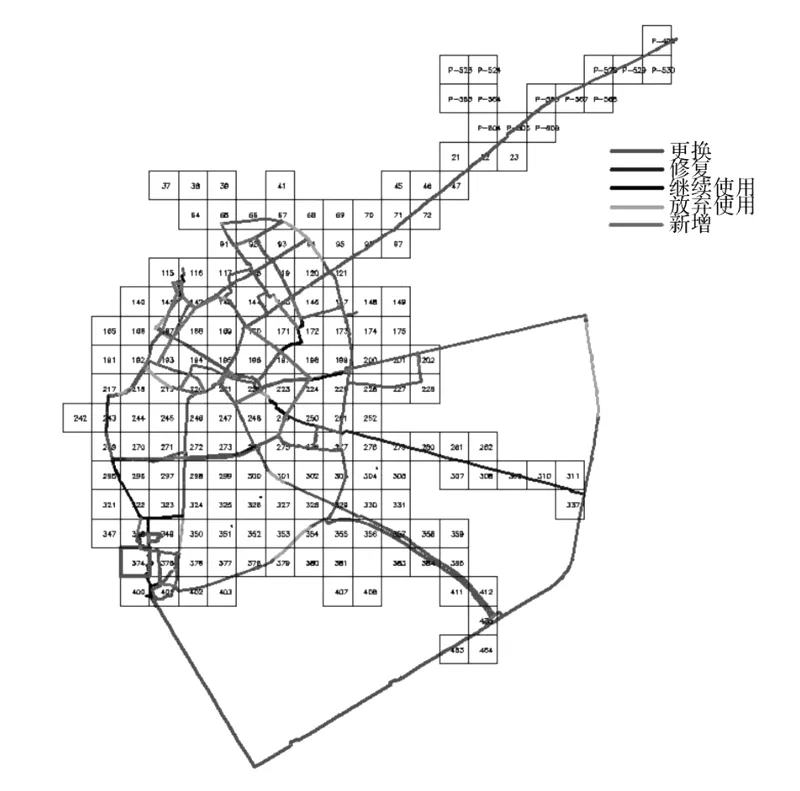
圖8 都江堰市供水管網恢復重建方案

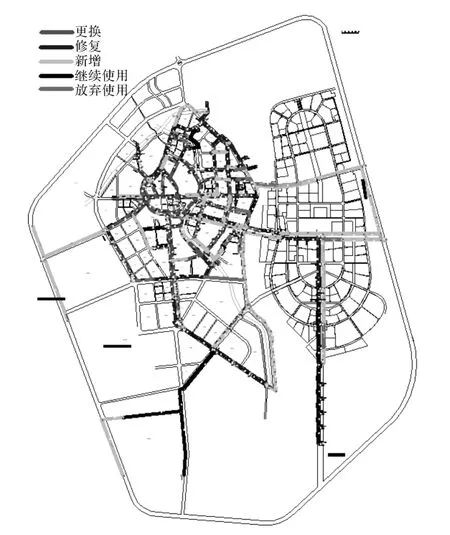
圖9 綿竹市供水管網恢復重建方案

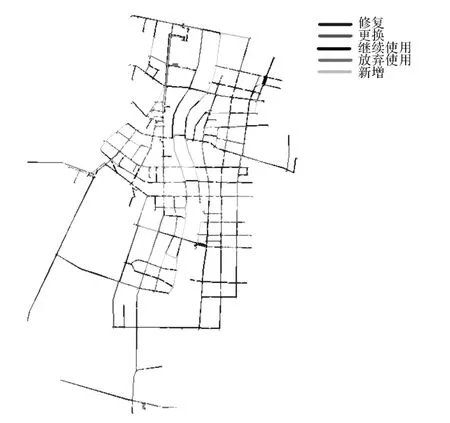
圖10 德陽市供水管網恢復重建方案

本文以抗震連通可靠度為約束建立了一般生命線工程網絡的抗震拓撲優化模型,采用遺傳算法對這一模型進行了求解。同時,以抗震功能可靠度為約束建立了供水管網的抗震拓撲優化模型,并采用模擬退火算法進行了求解。實例分析表明,上述兩種算法均能較好地用于網絡的抗震拓撲優化分析之中。最后,利用模擬退火算法,對四川省三個城市的供水管網進行了拓撲優化分析,給出了其災后恢復重建方案。

[1] 李杰.生命線工程抗震——基礎理論與應用[M].北京:科學出版社.2005.

[2] 陳玲俐.城市供水管網系統抗震可靠性分析與優化[D].上海:同濟大學,2002.

[3] 包元峰,李杰.基于遺傳算法的生命線工程網絡抗震優化設計[J].防災減災工程學報,2006,26(1):21-27.

[4] Li Jie&He Jun,A recursive decomposition algorithm for network seismic reliability evaluation[J].Earthquake Engineering and Structural Dynamics,2002,31:1525-1539.

[5] Holland J H.Adaptation in Natural and Artificial Systems[M].M IT Press,1975.

[6] C Gazen,C Ersoy.Genetic algorithms for designing multihop lightwave network topologies[J].Artifical in intelligence engineering,1999,13:211-221.

[7] D Saha,M D.Purkayastha and A.Mukherjee.An approach to wide area WDM optical network design using genetic algorithm[J].Computer Communications,1999,22:156-172.

[8] 王烜.城市燃氣管線網絡系統優化設計研究[D].哈爾濱:哈爾濱工業大學,2005.

[9] 衛書麟,李杰.城市供水管網抗震功能可靠度分析[J].防災減災工程學報,2005,25(4):353-358.

[10]邵知宇.給水管網分段線性優化模型[D].上海:同濟大學,2001.

[11]Metropolis N,Rosenbluth A,Rosenbluth M et al.Equation of state calculations by fast computing machines[J].Journal of Chemical Physics,1953,21:1087-1092.

[12]Kirkpatrick S,Gelatt Jr C D,Vecchi M.P.Optimization by simulated annealing[J].Science,1983,220:671-680.