淺析BP神經網絡算法的改進和優化
儲琳琳 郭純生
摘要:本文簡要介紹了BP神經網絡的缺點,著重強調了BP神經網絡的算法改進,并且,利用Matlab仿真了各種改進算法的學習速度,從結果看改進后的BP神經網絡能較好地解決針BP算法學習速度慢的缺點。
關鍵詞:神經網絡;BP算法;學習速度
中圖分類號:TN430文獻標識碼:B
1BP算法的缺點
雖然神經網絡模型已成功應用于模式識別、函數逼近、時間序列預測等領域。并且BP網絡也是目前應用最為
廣泛的一種神經網絡模型,它具有思路清晰,結構嚴謹,可操作性強等優點。但是由于BP學習算法僅改變網絡的連接值和閥值,不改變網絡的拓撲結構,因此BP網絡在處理具體問題時還存在如下問題[1]:
1.1網絡的麻痹現象。在網絡訓練過程中,加權調得較大可能迫使所有的或大部分節點的加權和輸出較大,從而操作在S壓縮函數的飽和區,此時函數在其導數非常小的區域,即函數的導數值很小或趨近0,由于在計算加權修正量的公式中,這使得調節幾乎停頓下來,通常為了避免這種現象,將訓練速率減小,但又增加了訓練時間。
1.2網絡學習收斂速度比較慢。由于BP算法的學習復雜性是樣本規模的指數函數,如果網絡規模較大或學習樣本較多時,往往需要很長的學習時間,甚至學習無法完成,這個主要由于學習速率太小所造成的;可采用變化的學習速率或者自適應的學習速率加以改進。
1.3易陷入局部極小值。BP算法可以使網絡權值收斂到一個解,但它并不能保證所求解為誤差超平面的最小解,很可能是局部極小解;這是因為BP算法采用的是梯度下降法,訓練是從某一起點沿誤差函數的斜面逐漸達到誤差的極小值,對于復雜的網絡,其誤差函數為多維空間的曲面,就像一個碗,其碗底是最小值點,但是這個碗的表面凹凸不平的,因而在對其進行訓練的過程中,可能陷入某一小谷區,而這一小谷區產生一個局部最小值,由此點向各個方向變化均使誤差增加,以至于使訓練無法逃出這一局部最小值。
為了解決BP網絡訓練的以上缺點,人們提出了多種有益的改進。改進方法主要有兩類:第一類是基于啟發式學習方法的改進算法:如附加動量的BP算法、自適應學習率BP算法、彈性BP算法等;第二類是基于數值優化的改進算法:如共扼梯度法、擬牛頓法和Levenberg-Marquardt(LM)法等。這些方法在不同程度上提高了學習速度,加
快了網絡的收斂,避免陷入局部極小值[2][3]。
2各種改進算法的學習速度的比較
在Matlab6.5中,通過調用newff實現網絡的創建,然后調用函數train對所創建網絡newff進行訓練。設定系統總誤差為0.01,步長為0.02,網絡訓練2000次,或直到滿足性能要求時停止訓練,否則增加訓練次數。表1給出幾種算法收斂速度的比較:表中的數據均為6次平均值。

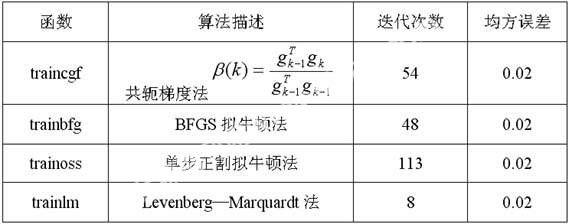
從表1和表2可以看出:
2.1基于啟發式學習方法的改進算法的收斂速度依次加快,其中彈性BP算法的收斂速度要比前兩種方法快得多。
2.2基于標準數值優化方法的各種改進算法均比基于啟發式學習方法的改進算法在收斂速度上有很大的提高,其中Levenberg-Marquardt法的收斂速度最快。
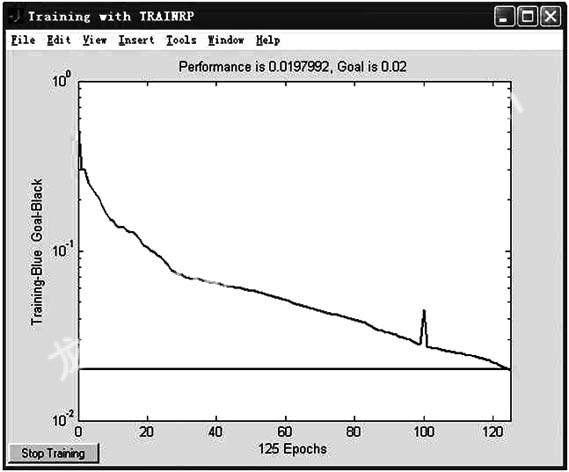
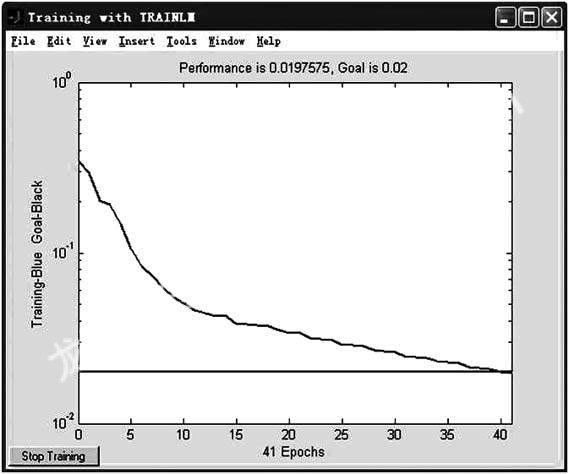
下面是在相同條件下,標準BP算法,彈性BP算法和Levenberg-Marquardt法對本電路進行網絡訓練的學習誤差變化曲線。
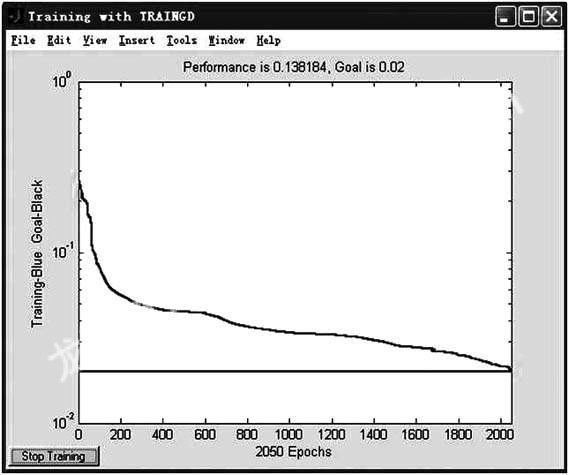
3結論
由實驗結果可知:
在基于啟發式學習方法的改進算法中,彈性BP算法的收斂速度快,算法并不復雜,也不需要消耗更多的內存空間,在實際應用中,是一種行之有效的算法。
在基于數值優化方法的各種改進算法中,Levenberg-Marquardt法和擬牛頓法因為要近似計算海森矩陣,需要較大的存儲量,通常收斂速度快。其中,Levenberg-Marquardt法結合了梯度下降法和牛頓法的優點,性能更優,收斂速度最快,對于中等規模的BP神經網絡具有最快的收斂速度,而且它很好地利用了MATLAB中對于矩陣的運算的優勢,因此它的特點很適合在MATLAB中得到體現;但是要存儲海森矩陣的值,所以該算法的最大缺點就是占用的內存量太大。共軛梯度法所需存儲量較小,但收斂速度較前兩種方法慢。所以,考慮到網絡參數的數目(即網絡中所有的權值和偏差的總數目),在選擇算法對網絡進行訓練時,可遵循以下原則[4]:
3.1在對訓練速度要求不太高,內存存儲量有限時,可使用彈性BP算法。
3.2在對訓練速對要求較高的情況下,網絡參數較少時,可以使用牛頓法或Levenberg-Marquardt法;在網絡參數較多時,需要考慮存儲量問題時,可以選擇共軛梯度法。
參考文獻:
[1]史忠科.神經網絡控制理論[M].西北工業大學出版社,1997(11).
[2]虞和濟,陳長征等.基于神經網絡的智能診斷[M].北京:冶金工業出版社,2000.
[3]朱大奇.電子設備故障診斷原理與實踐[M].北京:電子工業出版社,2004.
[4]王永驥,涂健.神經元網絡控制[M]北京:機械工業出版社,1998.

