《倍數(shù)和因數(shù)》第一課時教學(xué)設(shè)計

李　鵬

一、 教材簡釋

本課教學(xué)內(nèi)容是蘇教版小學(xué)數(shù)學(xué)四年級下冊第70～72頁內(nèi)容。教材第一個例題要求學(xué)生分組用12個同樣大的正方形拼成一個長方形，在充分操作的基礎(chǔ)上引導(dǎo)學(xué)生用乘法算式把自己的擺法表示出來，為討論倍數(shù)和因數(shù)的概念提供素材。隨后教材結(jié)合一道具體的乘法算式，向?qū)W生說明倍數(shù)和因數(shù)的含義。第二個例題主要引導(dǎo)學(xué)生探索找一個數(shù)的倍數(shù)的方法，第三個例題主要引導(dǎo)學(xué)生探索找一個數(shù)的因數(shù)的方法，想想做做主要幫助學(xué)生鞏固對倍數(shù)因數(shù)的理解，進一步體會確定一個數(shù)的倍數(shù)或因數(shù)的方法。

二、 目標預(yù)設(shè)

1.從操作活動中理解倍數(shù)和因數(shù)的意義，掌握找一個數(shù)的倍數(shù)和因數(shù)的方法，發(fā)現(xiàn)一個數(shù)的倍數(shù)、因數(shù)中最大的數(shù)、最小的數(shù)及其個數(shù)方面的特征。

2.培養(yǎng)學(xué)生抽象概括的能力，滲透事物之間相互聯(lián)系、相互依存的辨證唯物主義的觀點。

3.培養(yǎng)學(xué)生的合作意識、探索意識及積極的數(shù)學(xué)情感。

三、 學(xué)重點

使學(xué)生從操作活動中理解倍數(shù)和因數(shù)的意義，掌握找一個數(shù)的倍數(shù)和因數(shù)的方法。

四、教學(xué)難點

發(fā)現(xiàn)一個數(shù)的倍數(shù)、因數(shù)中最大的數(shù)、最小的數(shù)及其個數(shù)方面的特征。

五、 設(shè)計理念

本節(jié)課中教師通過動畫片導(dǎo)入，采用情知互促的方法讓學(xué)生感悟到生活中像大頭兒子和小頭爸爸之間的父子關(guān)系與兩數(shù)之間的倍、因數(shù)關(guān)系間的巧妙聯(lián)系，從而對新知產(chǎn)生積極的學(xué)習(xí)情感。課上積極探索，新知是學(xué)生自己探索、發(fā)現(xiàn)、理解、掌握的，雖然一路走來“磕磕碰碰”，但每位學(xué)生都會在其中獲得豐富的情感體驗，教師又通過改變內(nèi)容、練習(xí)的呈現(xiàn)方式，保持、激發(fā)學(xué)生的學(xué)習(xí)情感。

六、 設(shè)計思路

課前動畫導(dǎo)入激起學(xué)生的學(xué)習(xí)興趣，讓學(xué)生在潛移默化中體會到何謂相互聯(lián)系、相互依存的關(guān)系，為后續(xù)的學(xué)習(xí)打下基礎(chǔ)。

在新授環(huán)節(jié)中引導(dǎo)學(xué)生操作實踐，于無意中滲透“一對一對地找一個數(shù)的因數(shù)”。同時，為加深學(xué)生對倍數(shù)和因數(shù)的認識，我特意設(shè)計了一道除法算式，旨在通過討論、交流，使學(xué)生獲得啟發(fā)：找一個數(shù)的倍數(shù)或因數(shù)既可以用乘法，也可以用除法。

在教學(xué)找一個數(shù)的倍數(shù)時,采用邊扶邊放的教學(xué)策略。通過學(xué)生無序地交流、教師有意識地板書，引導(dǎo)學(xué)生發(fā)現(xiàn)有序思考的方法。

教學(xué)找一個數(shù)的因數(shù)時采取完全放開的教學(xué)策略。設(shè)計比賽這一環(huán)節(jié)，是為了讓學(xué)生在眾多的數(shù)中體會到一個數(shù)因數(shù)個數(shù)的多少與數(shù)的大小無關(guān)，并從中探索出一個數(shù)因數(shù)的特征。

“快樂大轉(zhuǎn)盤”融“玩”與知識的回顧、梳理、建構(gòu)于一體，讓學(xué)生在玩中盤點、運用知識，使之真切感受到數(shù)學(xué)源于生活。

七、 教學(xué)過程

一、 動畫導(dǎo)入，鋪墊激趣

師：同學(xué)們喜歡看哪些動畫片呢？李老師今天也帶了個動畫片，想看嗎？

（播放大頭兒子和小頭爸爸的動畫片）

師：剛才我們一起看了一段動畫，誰來說說大頭兒子和小頭爸爸是什么關(guān)系呢？（父子關(guān)系）（大頭兒子是小頭爸爸的兒子），反過來可以怎樣說？（小頭爸爸是大頭兒子的爸爸），那我和你們的關(guān)系？可以怎樣說？（李老師是我們的老師，我們是李老師的學(xué)生）人與人之間存在著各種相互依存、相互聯(lián)系的關(guān)系，在數(shù)學(xué)中，數(shù)與數(shù)之間同樣也存在著這樣的關(guān)系。

[設(shè)計意圖：課前動畫導(dǎo)入一下子激起了學(xué)生的學(xué)習(xí)興趣，另一方面讓學(xué)生在潛移默化中體會到何謂相互聯(lián)系、相互依存的關(guān)系，為后續(xù)的學(xué)習(xí)打下基礎(chǔ)。]

二、 操作實踐，理解意義

師：今天，小頭爸爸給大頭兒子出了一道題：你能用12個同樣大的小正方形拼成一個長方形嗎？請同學(xué)們?nèi)〕鲂欧饫锏男≌叫危覀円瞾砥匆黄矗瑪[一擺。

交流：

（1）你是怎樣擺的？誰能根據(jù)他的擺法說一個乘法算式？

（2）你拼成的長方形可以怎樣列式？猜猜他可能是怎樣擺的？（課件出示相應(yīng)的圖形）

師：通過剛才的操作，我們發(fā)現(xiàn)，用12個同樣大的小正方形可以擺出三種不同的長方形，由此我們還得到了這3個不同的乘法算式。以3×4=12為例，我們可以說3是12的因數(shù)，12是3的倍數(shù)。4是12的因數(shù)，12是4的倍數(shù)。

師：你能根據(jù)另外兩道算式照樣子說一說嗎？

師：這道算式（板書：18÷3=6）你們會說嗎？同桌先商量一下。（指名說）

師：看來我們不僅能在乘法算式中找到一個數(shù)的倍數(shù)和因數(shù)，也能在除法算式中找到一個數(shù)的倍數(shù)和因數(shù)，這節(jié)課我們就一起來研究。為了方便，我們在研究倍數(shù)和因數(shù)時，所說的數(shù)一般指不是0的自然數(shù)。

[設(shè)計意圖：引導(dǎo)學(xué)生操作的目的是于無意中滲透“一對一對地找一個數(shù)的因數(shù)”的方法。同時，為了加深學(xué)生對倍數(shù)和因數(shù)的認識，我特意設(shè)計了一道除法算式，旨在通過討論、交流，使學(xué)生獲得啟發(fā)：找一個數(shù)的倍數(shù)或因數(shù)既可以用乘法，也可以用除法。]

三、 探索方法，有序思考

1.找一個數(shù)的倍數(shù)。

師：通過剛才的學(xué)習(xí)，我們已經(jīng)知道12是3的倍數(shù)，18也是3的倍數(shù)，那3的倍數(shù)就只有12和18這兩個嗎？（不是）還有哪些呢？（學(xué)生可能會無序地說，教師有序地寫3的倍數(shù)），寫得完嗎？（寫不完，有無數(shù)個）一般我們只要寫出5個，其余用省略號代替。

師：剛才同學(xué)們是隨便說的，而老師是這樣按從小到大的順序?qū)懙模阌X得哪個好？為什么？（出示：有序）

師：你能有序地找其它一些數(shù)的倍數(shù)嗎？（請打開書本，完成71頁上的“試一試”）

觀察探索：觀察2、3、5的倍數(shù)，你發(fā)現(xiàn)一個數(shù)的倍數(shù)有什么特點？

課件出示表格左半部分：

[設(shè)計意圖：本部分內(nèi)容擬采用邊扶邊放的教學(xué)策略。通過學(xué)生無序的交流、教師有意識的板書，引導(dǎo)學(xué)生發(fā)現(xiàn)有序思考的方法；之后讓學(xué)生獨立找2、5的倍數(shù)，并且通過綜合觀察，比較得出一個數(shù)倍數(shù)的特點。]

2.找一個數(shù)的因數(shù)。

師：我們已經(jīng)會有序地找一個數(shù)的倍數(shù)，那你們會找一個數(shù)的因數(shù)嗎？讓我們一起試著找一找18的因數(shù)。（學(xué)生匯報，師板書）

師：你是怎樣找18的因數(shù)的？（除法、乘法口訣）在找18的因數(shù)時有什么好辦法可以既不重復(fù)又不遺漏？（探索一對一對地找的方法）

師：你能這樣一對一對地找出36的因數(shù)嗎？（學(xué)生匯報，師板書）

師：在50以內(nèi)，每人任意挑一個自然數(shù)，比一比，誰找的數(shù)的因數(shù)的個數(shù)最多？誰找的數(shù)的因數(shù)的個數(shù)最少？（交流）

觀察探索：你發(fā)現(xiàn)一個數(shù)的因數(shù)有什么特點？

出示表格右半部分：

[設(shè)計意圖：找一個數(shù)的因數(shù)采取完全放開的教學(xué)策略。設(shè)計比賽這一環(huán)節(jié)，是為了讓學(xué)生在眾多的數(shù)中體悟到一個數(shù)因數(shù)個數(shù)的多少與數(shù)的大小無關(guān)，并從中探索出一個數(shù)因數(shù)的特征。]

小結(jié)：這節(jié)課你有什么收獲？

四、實踐應(yīng)用，拓展延伸

1.真假我來辨。

（1）因為2×3=6，所以2是因數(shù)，6是倍數(shù)。（）

（2）17最小的倍數(shù)是34。（）

（3）6既是2的倍數(shù)，又是3的倍數(shù)。（）

（4）20的最小倍數(shù)和最大因數(shù)都是它本身。（）

（5）3的最大倍數(shù)是18。（）

（6）20以內(nèi)3的最大倍數(shù)是18。（）

2.完成教材72頁想想做做第2題，第3題。

師作適當點評。

3.快樂大轉(zhuǎn)盤。

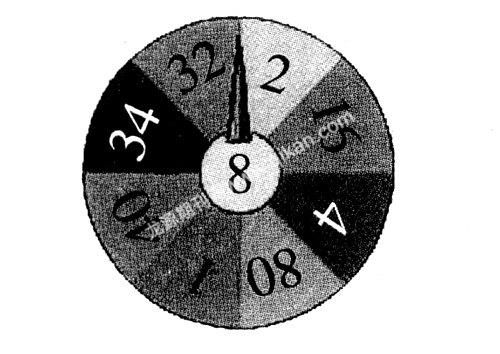
師：接下來我們來玩一個快樂大轉(zhuǎn)盤的游戲。

游戲1：轉(zhuǎn)盤指針轉(zhuǎn)到哪個數(shù)，請同學(xué)們舉手搶答：用倍數(shù)和因數(shù)的知識說兩句話表示這兩個數(shù)之間的關(guān)系。

游戲2：接下來，李老師想請兩小組同學(xué)以開火車的形式比一比，哪組同學(xué)說得又快又對，若碰到重復(fù)的數(shù)可以繼續(xù)說（因為盡管轉(zhuǎn)到了相同的數(shù)，但前后學(xué)生不是同一人，同樣可以進行練習(xí)）

游戲3：請同學(xué)們?yōu)槔罾蠋煛稗D(zhuǎn)”出一個數(shù)，然后我根據(jù)這個數(shù)出道題考考同學(xué)們。（16）請學(xué)號是16的因數(shù)的同學(xué)起立！（若接下來的操作中又一次轉(zhuǎn)到16，就可以出“學(xué)號是16的倍數(shù)的同學(xué)起立”。實際上轉(zhuǎn)到16，就可以進行兩次游戲，一個是16的因數(shù)，一個是16的倍數(shù)。學(xué)生參與量就多了，可多次練習(xí)）

誰能運用今天所學(xué)的知識說一句話讓全班同學(xué)都起立？（學(xué)號是1的倍數(shù)的同學(xué)起立）。

[設(shè)計意圖：融“玩”與知識的回顧、梳理、建構(gòu)于一體，讓學(xué)生在玩中盤點、運用知識，使之真切感受到數(shù)學(xué)源于生活，不僅好玩而且生動有趣。]