《用倒推的策略解決問題》教學設計

陳　蕾

教學內容：蘇教版義務教育課程標準實驗教科書數學五年級下冊第88-89頁

教學目標：

1．使學生通過分析具體情境中的實際問題，體驗“倒過來推想”的策略解決特定問題的價值，初步學會運用“倒過來推想”的策略尋找解決問題的思路，并能根據問題的具體情況確定合理的解題步驟。

2．使學生在對解決實際問題過程的不斷反思中，進一步發展分析、綜合和進行簡單推理的能力。

3．使學生進一步積累解決問題的經驗，增強解決問題的策略意識，獲得解決問題的成功體驗，提高學好數學的信心。

教學重點：

學會運用“倒過來推想”的策略尋找解決問題的思路，并能根據問題的具體情況確定合理的解題步驟。

教學準備：

掛圖 課件水杯

教學過程

一、 教學例1

1．呈現問題。

（1）出示“原來的”兩杯果汁，并出示條件“兩杯果汁共400毫升”。

提問：如果把甲杯中的40毫升果汁倒入乙杯，這兩杯果汁的數量分別會發生怎樣的變化？

（2）學生回答上述問題后進行實際的操作演示，讓學生發現不僅甲杯減少了乙杯增加了，而且甲杯和乙杯正好同樣多。

（3）回顧操作過程，出示例題中條件部分的完整示意圖，提出問題：原來兩杯果汁各有多少毫升？

2．解決問題。

（1）提問：把甲杯中的40毫升果汁倒入乙杯后，兩個杯子里的果汁總量有沒有變化？現在每個杯子里各有多少毫升果汁？

（2）小組討論：知道了現在兩個杯中的果汁數量，可以怎樣求原來兩個杯中的果汁數量？可以用怎樣的方法來解決？

（3）在學生提出“再倒回去看一看”時，追問：如果把乙杯中的40毫升果汁再倒回甲杯，兩個杯中的果汁數量又會發生怎樣的變化？

（4）學生畫圖后，組織展示、交流，并相機呈現教材提供的第二組示意圖。

引導學生認識到“再倒回去”后，甲杯在200毫升的基礎上，增加了40毫升；乙杯在200毫升的基礎上，減少了40毫升。

（5）小結：看來“再倒回去”是個好辦法，用這個辦法我們很容易就能想到原來兩個杯子里各有多少毫升果汁。

3．填表回顧，加深對“倒過來推想”的體驗。

（1）回想一下，我們剛才是怎樣解決這個問題的？你能按照解題的過程將課本中的表格填寫完整嗎？要求邊填邊想表中的每個數據各是怎樣推算出來的。

（2）提問：在解決這個問題的過程中我們運用了哪些策略？你認為“倒過來推想”的策略有什么特點？

學生討論后，揭示課題并板書：用倒推的策略解決問題。

二、 教學例2

1．出示例2，讓學生讀題后，再要求說說題目的大意。提問：用什么方法可以將題目的意思更清楚地表示出來？

2．在學生討論后，指出：可以按題意摘錄條件進行整理。出示：

原有？張→又收集了24張→送給小軍30張→還剩52張

提問：你能根據上圖再說說題目的大意嗎？要求小明原來有多少張郵票，你準備用什么策略來解決？

3．明確可以用“倒過來推想”的策略解決問題后，提出：你能仿照上圖的樣子，表示出“倒過來推想”的過程嗎？

學生嘗試畫出倒推的示意圖后，交流：

原有？張← 去掉收集的24張← 跟小軍要回30張←還剩52張

要求根據上圖寫出倒推后每一步的結果，再讓學生綜合“倒過來推想”的過程列式解答。

4.簡化思路：根據小明郵票張數的變化情況，也可以畫出下面的流程圖：

同時啟發學生思考：有沒有其他的方法？（轉化出“又搜集的比送出的少6張”，可以得出什么算式？還可以列方程來解答。）

5.檢驗：要求學生根據答案和“小明郵票張數”的變化情況順推過去，看看剩下的是不是52張。在順推和倒推的對比中，進一步認識倒推策略。

6.反思：解決上面這個問題時，是怎樣運用“倒過來推想”的策略的？你認為適合用“倒過來推想”策略來解決的問題有什么特點？

三、 應用鞏固

1. 練一練。

學生各自讀題。提問：你打算用什么樣的策略解決這個問題？“拿出畫片的一半還多1張送給小明”是什么意思？你能換種說法表示這樣的意思嗎？

畫一畫：

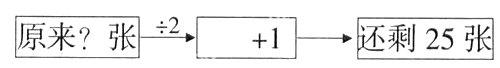
學生解題后，組織交流，重點讓學生說說推想的過程。

2.填一填。

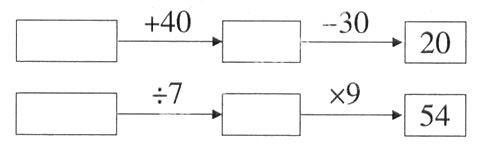
3.想一想。

（對話）一位旅行者看到牧羊人在放牧，問他：“你這群羊有多少只？”牧羊人回答：“把我這群羊的只數減去７，除以５，再加上８，乘以４，正好是１００。請你算算，我有多少只羊？”

四、 課堂作業

做練習十六的第1、2題。

要求學生借助列表或者畫流程圖的方法整理信息，自主解題。

五、 全課小結

通過這節課的學習，你有哪些收獲和體會？

游戲解密。你知道老師是怎樣猜數了吧？

【設計說明】策略的學習，不能脫離解決問題的過程。有人說策略是問題解決的副產品。在把問題的最終解決作為目的時，策略的總結確實在其次，然而這從數學學習的發展目標來看又是本末倒置的。問題的解決只是數學學習的必要途徑，不是學習的歸宿。知識的背后是方法，方法的背后是思想。所以說，策略的學習基于解決問題，又不能囿于解決當前問題。“倒過來推想”是一種特殊策略，是特定問題情境下解決問題的策略，由于這種特定的問題情境比較常見。通常已知某種數量或事物按照明確的方法和步驟發展、變化后的結果，又要追溯它的原始或起始狀態，就需要這種策略，學習這種策略，不僅豐富學生的策略模型積累，而且可以在更大范圍中培養學生的思維靈活性和深刻性。

在這個教學設計中，先用有趣的猜數游戲引發學生的興趣，喚醒學生從數學的角度來解密。在例題的學習中，分兩個層次來彰顯策略：首先是例1的初步感受，使學生走出混沌；其次是例2的初步運用，促使學生思維更加明朗和深刻。在交流其他解法中整合以往學習的解決問題的策略應用，檢驗環節也能在順推和倒推的對比中進一步認識倒推的策略。在鞏固階段，緊扣學生剛剛認識的“倒過來推想”策略集中強化，加深學生對策略的理解和掌握，逐步達到自主自覺運用策略的境界。整個設計立足數學素養的整體建構，從問題回饋策略，又從策略服務問題，前后呼應，一氣貫通。