兩位教師的反比例函數教學

張　勝

最近聽了學校里兩節反比例函數教學的公開課，感受頗深.眾所周知，函數概念的“學”離不開教師的“教”，那么教師的課堂教學對學生函數概念的學習有什么樣的影響?帶著這樣的問題，本文對這二節公開課(一位新手教師和一位經驗教師)的函數課堂教學進行了分析，以尋找課堂教學對學生函數學習的影響因素.

1.教材的學習目標

我們學校采用的是山東教育出版社出版的義務教育課程標準試驗教科書，教材中規定的反比例函數的學習任務，一是要求學生從現實情境和已有知識經驗出發，討論兩個變量之間的相依關系，加深對函數概念的理解；二是要求學生經歷抽象反比例函數的過程，領會反比例函數的意義，理解反比例函數的概念；三是要求學生能夠作出反比例函數的圖像，逐步提高從函數圖像中獲取信息的能力.本堂課的類型屬于新授課.

2.教師的課堂教學

(1)整體結構與時間分布

從課堂教學的整體結構來看，新手教師和經驗教師都經歷了“引入反比例函數的概念——反比例函數練習——反比例數圖像——小結”.

但有兩個明顯差異，一是新手教師在“反比例函數練習”中分兩步走，引導學生區分一次函數和反比例函數后，立即進行習題訓練，新手教師似乎更相信只有通過“練習”，學生才能學習和掌握反比例函數的概念；而經驗教師則分了三步走，多了“讓學生列舉生活中反比例函數的例子”這個過程，經驗教師可能更相信反比例函數的理解是首要條件，練習只是檢查學生是否掌握概念的手段.差異之二表現在兩位教師對反比例函數圖像的講解有所不同，經驗教師教學時注重回顧先前的作圖知識，并能根據圖像的內容選擇恰當的教學方法，講授的難度也更深.

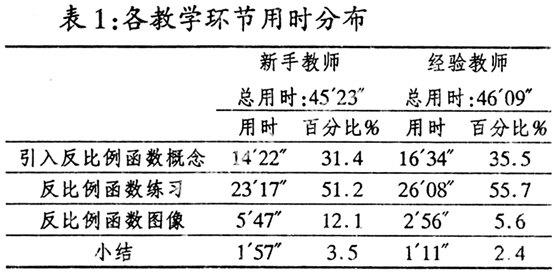
從課堂教學的時間分配上可以看出，新手教師和經驗教師都有超過一半以上的時間放在函數概念的練習上，經驗教師將練習重點放在“讓學生列舉生活中反比例函數的例子”上， 并且經驗教師在“引入反比例函數概念”環節投入的時間比新手教師多4.1個百分點.

(2)反比例函數概念的建立

新手教師從實際問題情境入手，引導學生列出函數關系式，并指出這些式子的共同點，最后總結反比例函數的概念.在新手教師的教學過程中，教師總結概念的過程，采取的是發現共同點的歸納總結，其教學過程是：

①提出一系列問題；

②要求列出函數關系式；

③追問自變量取值范圍及單位是否統一；

④提出問題：這些式子有什么共同點；

⑤從解析式的形式上概括反比例函數概念；

⑥總結反比例函數兩變量的取值范圍.

在建立反比例函數概念時，新手教師提出的教學任務強調的是學生的“求同”探索，試圖讓學生發現反比例函數定義形式上的共同點，該任務有以下三個特征：

①創設了問題情境，有助于學生對反比例函數的理解；

②要求“發現函數關系式的共同點”，暗示學生可以從解析式入手總結歸納概念；

③學生需要某種程度的認知努力，才能更好的理解反比例函數.

經驗教師也是從具體的情境著手，但由于使用了課件，所以教師向學生展示了更多的問題實例，列出的函數關系式有一次函數和反比例函數兩種類型，并借此總結了正比例函數與反比例函數的區別.在反比例函數概念的學習中，教師對學生的認知提出了較高要求，學生對此給出的答案也是多樣的，具有“求同辨異”的特點.其教學過程是：

①課件展示問題情境；

②要求學生列出函數關系式；

③追問另一個學生正確的表達式；

④強調單位統一和自變量的取值范圍；

⑤課件展示問題答案；

⑥提出問題：用自己的語言敘述什么樣的式子是反比例函數；

⑦追問學生正比例函數與反比例函數的不同點；

⑧在函數解析式和自變量取值范圍的比較中總結兩者的區別.

可見，該教師教學過程的一個重要特點是，提及了正比例函數，將新知識反比例函數的學習與舊知識聯系起來.該任務的特征是：

①為了發展對反比例函數概念的更深層次理解，學生的注意力集中在正比例函數與反比例函數的比較；

②創設了問題情境，在正比例和反比例函數兩種表現形式之間建立起有助于意義理解的聯系；

③學生在比較中產生認知沖突，需要一定認知努力才能更好發展對反比例函數的理解.

3.教師影響學生學習任務實施的因素分析

在新手教師的課堂中，教師始終從思路上引導學生，保持與學生積極互動的問答，加深學生對反比例函數概念的理解，所以學生在學習時，基本保持了較高的認知水平.教師使學生的學習任務得以保持高認知水平的因素有3個，使其下降的有2個.

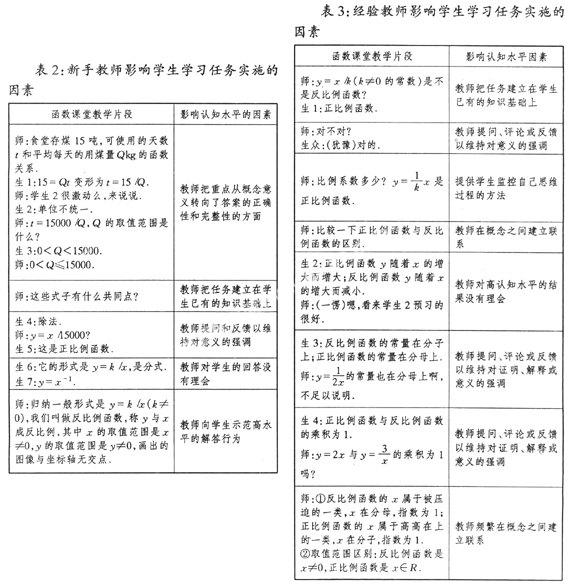
從表2中可以看出，在“理解反比例函數”過程中，學生往往用“除法”、“分式”這樣一些詞去概括反比例函數，這是因為教師將學生列出的函數關系式有預備性的加以代數化，試圖搭建一種“聯系”，并且在概念引入的時候，教師通過提問、解釋和反饋引導學生積極探究.在整個學習過程中，教師保持了學生的高認知水平，主要表現在以下幾個方面：

①任務建立在學生已有的函數關系式知識基礎上；

②給予學生適當探索發現的時間；

③教師提問以提供學生反思自己思維的方法；

④教師對學生的回答予以反饋以維持對解釋的強調.

在經驗教師的課堂教學行為中，有7處保

持了“理解反比例函數概念”學習任務的認知水平，使其下降的因素有一個，如表3所示.在整個學習過程中教師也保持了學生的高認知要求水平，主要表現在以下幾個方面：

①任務建立在學生已有的正比例函數知識基礎上；

②給予學生適當的比較探索的時間；

③教師提問、評論或反饋學生的回答以維持對概念理解的強調；

④教師頻繁在正比例函數和反比例函數之間建立聯系.

4.課堂教學對學生函數學習的影響

(1)教學具有大致相同的整體教學結構，并且學生學習的過程大體保持了高認知水平，說明課堂教學有利于學生認知水平的發展與建構.

(2)從課堂教學的整體結構上看，新手教師定位在“概念練習”，經驗教師定位在“概念理解”.

(3)在引入反比例函數概念時，新手教師采用總結歸納的方法，發現概念的共性，具有“求同性”的特點；而經驗教師提出比較正比例與反比例函數的任務，學生思維活躍，答案多樣，具有“求同辨異”的特點.這種在辨析中掌握概念的教學方法，更有利于學生區別不同類型的函數.

(4)新手教師使學生認知水平下降的主要因素是“把問題的意義與理解轉向強調答案的正確性和完整性”、“教師對學生高認知水平的結果沒有理會”；經驗教師使學生認知水平下降的因素主要是“教師包辦學生的思維和推理，并告訴他們如何解答”，這些因素在一定程度上影響了學生學習函數的興趣，缺乏對學生學習效果的反饋評價.