關于初中數學課堂教學方法的探討

甘　梅

數學是一門邏輯性思維較強的學科，數學教學是數學思維活動的教學，而課堂教學是教學工作的主要形式，課堂學習是學生獲得知識技能的主要途徑．教師要提高教學質量就應重視知識的組織方式，在課堂上應注意培養學生思維的靈活性、思維的深刻性、思維的廣闊性、思維的批判性，對于不同的內容，應采取不同的教學方式．

一、概念教學時應注意引導學生研究概念的形成過程

心理學研究表明，人的認識過程，是人們在已有知識的基礎上，通過遷回間接的途徑，去尋找問題的答案，是在對豐富的感性材料的處理中產生本質的、一般性的認識．學生的認識過程，同樣應遵循這一規律．因此對于數學概念的教學，在課堂上應注意引導學生按照思維過程的規律出發，重視概念的形成過程，結論的發現過程，方法的思考過程，給學生多一些思考的空間和時間，鼓勵學生多一些聯想多一些實驗，引導他們參與從發現問題，分析問題到解決問題的全過程．

如，在學習“線段的垂直平分線的性質定理”時，可以這樣引導學生研究概念的形成過程：

1．學生練習

（1）任意畫線段AB，再畫這條線段的垂直平分線；

（2）在線段的垂直平分線上任取一點P，連結PA、PB，在線段的垂直平分線上再任取一點K，連結KA、KB；

2．教師指導學生實驗

（1）分別量出線段PA、PB和KA、KB的長度并比較PA與PB、KA與KB的大小關系；

（2）學生說出自己的結論：PA=PB、KA=KB.

3．教師提出問題，引導學生進入思維情境之中

（1）從有限個點的作圖中得到“線段的垂直平分線上的點到線段兩端的距離相等”，那么“線段的垂直平分線上的任一點到線段兩端的距離是否都相等”?

（2）要求學生再在AB的垂直平分線上任取一些不同的點，并且按上述要求自己操作完成.

（3）學生獨立操作完成后回答：相等．

（4）老師進一步提出要求：你能證明“線段的垂直平分線上的點到線段兩端的距離相等”這個命題嗎?

4．指導學生論證并讓學生展示證明過程

5．教師下最后結論：通過證明可知“線段的垂直平分線上的點到線段兩端的距離相等”的命題成立．

整節課上課的過程中，由于強調了知識被發現的過程，學生的思維活動始終活躍積極．使學生體驗了由感性到理性的認識上的飛躍的過程．

二、概念教學時應注意培養學生的分析歸納的能力

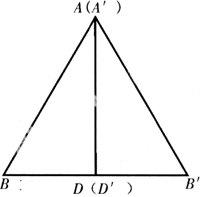
在概念教學中，應教會學生分析歸納的方法：如“軸對稱和軸對稱圖形”這兩個概念本身比較抽象，課本上的文字敘述也難理解，學生難以弄清兩者的聯系與區別．因而教學時，可首先引導學生自己動手實驗、操作，觀察現象：讓學生自己畫一個角、一個等腰三角形、一個等邊三角形、一個圓；再剪下來，對折，觀察其共同點．個人學習后，全班學習：先演示教具，講解圖形的特點，教師再概括：“這些圖形都具有特殊形狀，既都能沿一條直線對折，折疊后直線兩旁的部分能夠互相重合．也就是說，圖形和它本身重合，這樣的圖形叫做軸對稱圖形．這條直線就是它的對稱軸．軸對稱圖形可以只有一條對稱軸，也可能有幾條，乃至無數條對稱軸．”在教師引導下，學生通過個人學習和全班學習，對“軸對稱圖形”的定義，不僅有了感性認識，而且對定義中的三個要點：對稱軸、翻轉180°、圖形和它本身重合有了正確而清晰的認識．進而再引導學生進行個人獨立學習：把等腰三角形沿著頂角平分線剪開，成了兩個三角形，設為△ABD和△A′B′D′(見右圖)，觀察研究這兩個三角形的特殊位置關系．在個人學習的基礎上，再讓學生小組研究：軸對稱和軸對稱圖形的聯系和區別，并用教具在全班演示講解．通過以上的個人實驗、研究，全班交流、歸納，小組討論、辨析，學生從具體到抽象，對兩個概念的內容、實質、聯系和區別搞清楚了．這節課即突破了難點，也加深了對這兩個概念的理解，更重要的是整節課都讓學生處在不斷地體會觀察——分析——歸納的過程，使學生的分析歸納能力得到了提高．

三、教學時應注意加強逆向思維的訓練

許多數學知識都具有可逆結構，因此在數學教學中應加強逆向思維的訓練，這樣做不僅可以加深對原有知識的理解，而且還能發現一些新規律，對提高學生的思維能力十分有益．學生往往對問題習慣于正向思維，而忽略逆向思維，在遇到正向思維難以解決的問題時不會轉換為逆向思維去解決．往往使有些題目不得而解．所以在教學中就要善于指導學生學會運用逆向思維去思考問題，解決問題．例如，在學習完全平方公式(a±b)²=a²±2ab+b²時，可以下面的題目來訓練學生的逆用完全平方公式．

題目1:已知：e+1/e=3，求e²+1/e²的值.

分析：由題可知，直接利用已知條件去求e²+1/e²的值不大可能，但此題若能逆用完全平方公式則很快得解．

解：∵e²+1/e²=e²+2?e?1/e+1/e²-2?e?1／e

=(e+1/e)²-2

=3²-2

=7.

為了加深印象，又讓學生在第一題的基礎上做第二題：

題目2：已知：e+1/e=3，求e⁴+1/e⁴的值.

有了第一題的經驗，學生很快就得：

e⁴+1/e⁴=(e²+1/e²)²-2

=7²-2

=47.

接著又問：若已知e-1/e=3，是否也能求e²+1/e²和e⁴+1/e⁴的值?問題提出后，學生們感覺特別興奮，在互相議論后，很快通過逆用完全平方公式(a-b)²=a²-2ab+b²算出結果：

e²+1/e²=e²-2?e?1/e+1/e²+2?e?1/e

＝（e-1/e)²+2

=3²+2=11.

e⁴+1/e⁴=(e²+1/e²)²-2

=11²-2=119.

通過這樣的練習，使學生對完全平方公式有了進一步的理解，且訓練了學生對所學過的知識不僅僅習慣于正向思維，而且也要善于逆向思維，這樣的訓練，加深了對原知識的理解，對提高學生思維的靈活性、思維的深刻性、思維的廣闊性十分有益．

四、教學時要注意培養學生發散思維能力

發散思維是指從同一來源材料探求不同的解決問題的思維過程，思維方向發散于不同的方向，使思考者不拘泥于一個途徑，一種方法，求得多種合乎題意的方案，運用不同方法進行一題多解的練習，從而逐步培養學生舉一反三的能力．

如在學習“三角形中位線定理”這個內容時可采取以下的教學方法對學生進行發散思維的訓練：

(1)先引導學生閱讀課本中的推理論證過程；

(2)讓學生分組討論這個定理的其他不同的證明方法；

(3)各小組學生展示自己小組討論的結果；

(4)由教師歸納小結：“三角形中位線定理”各種不同的證明方法取決于所做的輔助線，輔助線的做法不同，證明的思路也不一樣．

通過這樣的教學過程，既對本節課所學的定理能加深理解，開闊學生的思路，提高分析問題的能力，又促進了學生思維能力的求異創新，對培養學生的發散思維能力很有好處．

總之，對不同的教學內容采取不同的教學手段是課堂教學成敗的關鍵，是教師傳授知識、培養學生能力的需要．因此它應成為我們深入研究的課題．