共頂點角問題分類探索

任南英

我們把頂點相同的角稱為共頂點角，與共頂點角有關的問題一般可分為角的計數問題、角的大小計算問題、角的邊的位置關系問題，所涉及的知識點是：角的和差倍分，互補、互余及對頂角等.

一、角的計數問題

由一個頂點發出若干條射線就可以組成一組共頂點角，這些角的個數一般與發出的射線條數有關，因為每兩條射線及它所夾的平面部分就可以組成一個角，由此看來這些角的個數的計算與共線線段條數的計算方法一樣(這也是由兩個端點及端點所夾部分的線組成)，若線段上共有n個點(包括它的端點)可組成1/(2n)（n-1）條線段，同樣從同一個頂點出發的n條射線(最大角小于平角)可以組成1/(2n)（n-1）個不同的角.

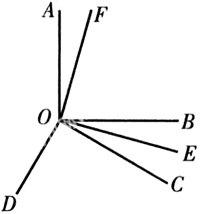
【例1】 如圖，已知∠AOB內，由O點發出6條射線，共組成不同的角(包括∠AOB)有幾個?

解析：從圖中可看出包括∠AOB的兩條邊OA、OB在內圖中共有8條射線，因此由這8條射線即n=8，共可組成不同的角共有1/(2n)（n-1）=1/2×8×(8-1)=28個.

說明：這類問題，得有一個前提最大角不超過180°,且所組成的角也只能是小于180°的角，否則就不行，想一想，為什么?

二、角的大小計算問題

1.角的和差倍分

【例2】 如圖，OC、OD、OE是∠AOB內的射線，OD平分∠AOB，OC平分∠BOD，∠DOE=13∠AOB，若∠COE=45°，求∠AOB的度數.

解析：設∠DOE=x°，則∠AOE=3x°，∠AOD=∠AOE+∠EOD=x°+3x°=4x°

∵OD平分∠AOB，

∴∠BOD=∠AOD=4x°.

又∵OC平分∠BOD，

∴∠COD=12∠BOD=12×4x=2x°,

∠COE=∠COD+∠DOE=2x°+x°=3x°,

由已知得∠COE=45°.

∴3x°=45°.

∴x=15.

又∠AOB=2∠AOD=8x°=8×15°=120°.

說明：一般在共頂點角問題中求角的大小均可采用設某個角的度數為未知數，從而可列出含未知數的方程來解，許多問題均可直接設所求角度為未知數(直接設法)，而本題卻是間接設元法.

2.互余問題

【例3】 已知OA⊥OB，OC⊥OD，OE⊥OF，∠AOD=146°，OE平分∠BOC，求∠AOF.

解析：設∠AOF=x,∵OA⊥OB,∴∠AOF+∠BOF=90°,

又∵OE⊥OF，∴∠FOB+∠BOE=90°，

∴∠BOE=∠AOF=x,

∵OE平分∠BOC，∴∠BOC=2∠BOE=2x,

而∠AOD+∠COD+∠BOC+∠AOB=360°，

∴146°+90°+2x+90°=360°,

解得x=17°,即∠AOF=17°.

說明：本題主要通過互余關系求解，當然還涉及周角問題；本題是采用直接設元法.

3.平角及互補問題

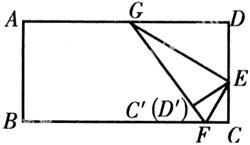
【例4】 如圖，ABCD為一張長方形紙片，先找到長方形紙的寬DC的中點E，將∠C過E點折任意一個角，折痕為EF，使EC與EC′重合，再將∠D過點E折起，使DE和D′E重合，折痕為GE.

(1)∠FEC和∠GED′互為余角嗎?為什么?

(2)上述折紙中，C點和D點折起之后，分別落在長方形的C′點和D′點.G、C′、D′和F是否在同一直線上?

解析：（1）∠FEC和∠GED′互為余角，由操作知，GE、EF分別是∠DEC′、∠CEC′的平分線.而∠DEC為平角，可知∠GEF=90°.因此，∠FEC和∠GED′互為余角.

（2）（略）.

說明：折疊問題的本質是軸對稱，成軸對稱的兩個圖形是全等圖形.

4.對頂角

從例4中我們知道在兩條直線相交所成的所有角中，有兩組對頂角和4組鄰補角.

【例5】 如圖,直線AB與CD相交于O，OB平∠DOF，OE⊥AB，O為垂足，∠1=50°，求∠AOC及∠COF.

解析：∵AB、CD相交于O，∴∠AOC=∠BOD，

又∵OE⊥AB,∴∠1+∠BOD=90°.

∴∠BOD=90°-∠1=90°-50°=40°,

∴∠AOC=40°.

∵OB平分∠DOF，

∴∠DOE=2∠BOD=80°，

∴∠COF=180°-∠DOF=180°-80°=100°.

5.平行線

在平行線的有關知識中，與共頂點角有關的知識不是比較多的，當然，一般的平行線中的共頂點角問題涉及到的知識點以對頂角居多，但也有一些問題例外，如下例題:

【例6】 如圖，若AB∥CD，則（）.

A.∠1=∠2+∠3

B.∠1=∠3-∠2

C.∠1+∠2+∠3=180°

D.∠1-∠2+∠3=180°

解析：過E作EF∥AB，

∴∠1+∠AEF=180°，又∵EF∥AB，AB∥CD，∴EF∥CD，

∴∠3+∠CEF=180°,即∠3+∠2+∠AEF=180°.

∴∠1=∠2+∠3，故選A.

說明：本題看似無共頂點角，但在解題過程中，通過輔助線添加而得到與∠2共頂點的∠AEF，并通過∠AEF的過渡完成解答，得到結果，當然本題也可通過延長BA交CE于一點來求解.