例談幾何問題的聯想與推廣

錢衛江

幾何證明可培養學生的發散思維能力，在初中幾何教學中是一個難點.為提高幾何的解題能力需要讓學生學會聯想與推廣.學習幾何離不開解題，但要學好幾何離不開歸納、總結.學生要善于歸納總結，題目解完了要勤于聯想，這樣才能真正學好幾何.下面結合實例，說明歸納、總結、聯想、推廣的方法.

例如圖1，從圓外一點P作切線PA，點B是PA上的中點，過點B作圓的割線BCD，連接PD交圓于點F，連接PC并延長，交圓于點E，求證：EF//PA．

分析：證明與圓有關的兩直線平行的問題，應先考慮是否存在內錯角、同位角相等，這是因為圓和三角形結合的圖形中，一般可通過弧、弦找到不少角之間的關系.由于題中相切與圖中線段直接相關，所以應聯想到用“線”成比例去證明角相等.

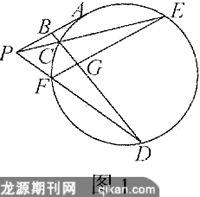
證明：∵PA切圓于A，點B為AP的中點，

∴AB２=BC·BD，AB=BP．

∴BP２=BC·BD，即BC/BP=BP/BD．又∠BPD=∠PBC，

∴△BPC∽△BDP． ∴ ∠D=∠BPC．

∵∠D=∠E， ∴ ∠BPC=∠E． ∴ EF//PA.

數學大師波利亞有一句名言:“掌握數學就是意味著善于解題.”善于解題關鍵要懂得解題后的反思，這個題目解完后有下列問題可供我們反思.

（1）實際上，由BP２=BC·BD，通過這個形式很容易聯想得到PB與△PCD的外接圓相切，切點是P．由弦切角定理得，∠D=∠BPC．又因∠D=∠E，所以∠BPC=∠E．故EF//PA.這個證明方法更簡捷，但對條件的處理和認識更深刻.

（2）據結果EF//PA，由夾在兩平行線間的弧相等可知，A點是弧FAE的中點.

（3）在圖中找與△PCB相似的三角形.通過相似可得很多相關的線段關系.

（4）嘗試對于一個命題的條件和結論互換是否仍然成立.若PA//EF，B是PA的中點嗎？根據上面的證明不難推出這個結論是成立的，于是引申出下列問題．

問題……