四輪驅動全輪差速轉向移動焊接機器人運動學分析與仿真
毛志偉 吳 訓 周少玲 李向春 鄧凡靈
1.南昌大學,南昌,330031 2.江西工業職業技術學院,南昌,330095
?
四輪驅動全輪差速轉向移動焊接機器人運動學分析與仿真
毛志偉1吳訓1周少玲2李向春1鄧凡靈1
1.南昌大學,南昌,3300312.江西工業職業技術學院,南昌,330095
摘要:為增加輪式移動焊接機器人穩定性、負載能力和降低控制復雜度,提出了一種四輪驅動全輪差速轉向移動焊接機器人機構,介紹了該機構差速轉向原理,證明該機構無轉向側滑。采用非完整約束方法建立了其差速轉向誤差模型,并在該模型基礎上對其進行了直線-圓弧-直線軌跡數值仿真,結果為轉角誤差0.002 137°,轉動中心坐標誤差小于0.012 mm。仿真結果表明該模型滿足焊接中的位置精度要求。
關鍵詞:四輪驅動移動機器人;全輪差速轉向;運動學模型;數值仿真
0引言
輪式移動機器人具有結構簡單、狀態穩定等特點,已經廣泛應用于機械工業等領域[1-2]。目前四輪輪式移動機器人轉向主要有滑移轉向、四輪驅動和四輪獨立轉向三種方式[3]。滑移轉向不需要單獨設計轉向機構,通過兩側輪子速度差來實現(如四輪驅動滑移轉向移動機器人),該方式由于存在側滑,其轉向精度和穩定性難以保證。四輪轉向方式一般應用在新型汽車中,這種方式操作方便,但結構較為復雜[4]。四輪獨立轉向能使轉向更為精確,Fischer等[5]針對較薄鋼質液化儲罐采用了四輪驅動四輪獨立轉向機器人;楊樹風[6]研制的一款帶有機械手臂的四輪全方位移動機器人亦是此種結構,但該轉向方式需要更多電機驅動,且控制復雜。
筆者在對各種轉向移動機器人分析的基礎上,結合焊接實際需要,提出了一種四輪驅動全輪差速轉向移動焊接機器人[7],該機器人機構采用全輪轉向原理,左右兩側的轉向各由一個電機驅動,且前后輪轉向角度大小相等,方向相反。該轉向方式可避免機器人轉向時側滑,機器人轉向精度與穩定性高,能滿足移動焊接要求。
為驗證機構正確性及為后續分析奠定基礎,分析了該機構無側滑條件,并建立了其運動學模型與誤差模型,采用MATLAB軟件以典型的直線-圓弧-直線焊縫為例進行了軌跡仿真分析。
1四輪驅動全輪差速轉向機構及原理
四輪驅動全輪差速轉向移動焊接機器人四輪驅動原理見圖1,其中移動焊接機器人主要結構包括4個驅動輪(驅動輪1~4),機器人本體5以及焊槍等。其運動副主要包括4個驅動輪繞各自軸的旋轉副,4個驅動輪與機器人本體5之間的旋轉副,以及驅動焊槍的十字滑臺中2個移動副。移動焊接機器人差速轉彎時左邊驅動輪的轉彎半徑如圖1中RL所示,右邊驅動輪的轉彎半徑如RR所示。
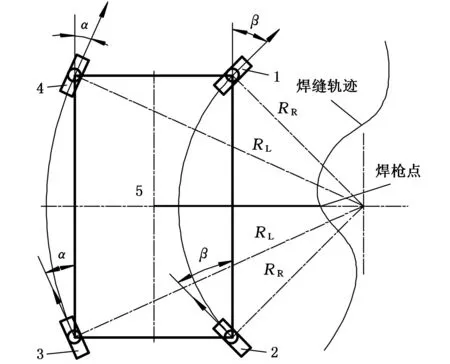
圖1 四輪驅動機器人差速轉向原理圖
四輪驅動全輪轉向移動機器人差速轉向時,驅動輪1與驅動輪2的速度vR大小與偏轉角β大小分別相同,但兩輪的偏轉角方向相反;驅動輪3、驅動輪4的速度vL大小相等,偏轉角α大小相同方向相反。設速度差Δv=vR-vL=0時,移動機構將沿直線運動;Δv<0時,移動機構將繞右側轉動中心轉動(圖1);Δv>0時,移動機構將繞左側轉動中心轉動。四輪差速轉向的特點是左側前后兩輪的速度vL大小、偏轉角β大小始終相同,右側兩輪的速度vR大小、偏轉角α大小始終相同,利用兩側輪子差速能實現繞任意半徑轉彎,轉向靈活、精度高、操作簡便、結構簡單,且無需轉向機構。
2無側滑條件及誤差模型的建立
2.1移動機器人無側滑條件
本文所提出的機器人機構轉彎時雖然不存在側滑,但必須滿足一定的條件。下面就該機器人無側滑條件進行分析。
移動機器人轉彎時,4個驅動輪狀態及坐標系oxy如圖2所示。左右兩側前后車輪轉角大小相等,方向相反。E為機器人質心,H為焊接點,O1為H點處焊縫軌跡曲率中心,A、B、C、D為各驅動輪與機器人本體間轉動副中心,F為AB中點,G為AD中點。設:LHO1=R0, LEH=d,LAD=LBC=2l,LAB=LCD=2b。H點坐標為(xH,yH)、速度為vH,vH與x軸夾角為θH,左側前后輪當前轉角為α,右側前后輪當前轉角為β,EH與x軸夾角為θ,AH與AB間夾角為φ。
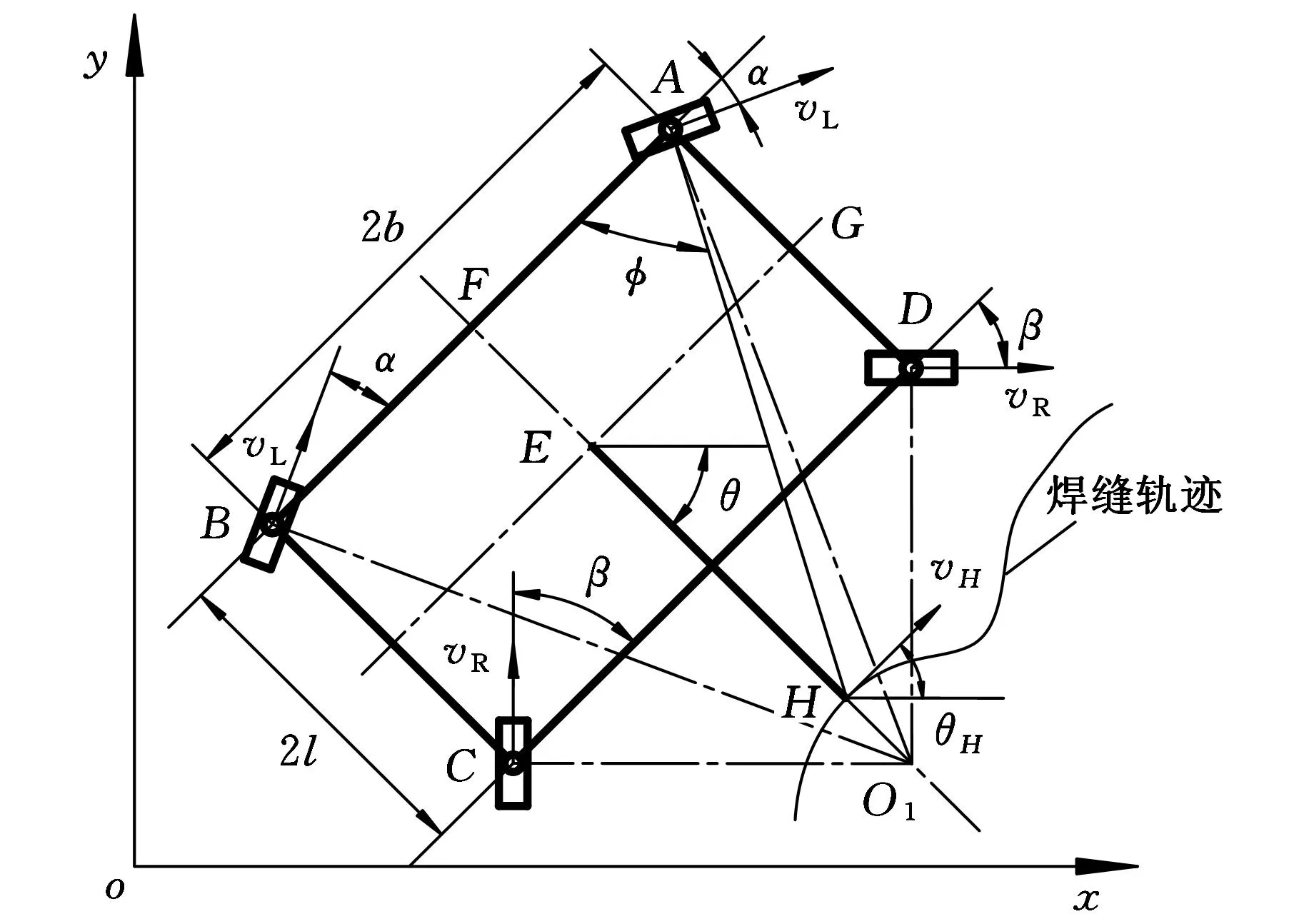
圖2 機器人無側滑差速轉向坐標系
根據無側滑條件可得機器人的質心方程:
(1)
相關約束條件如下。
(1)幾何約束:
(2)
(2)焊接約束。根據焊接工藝要求,焊接過程中vH沿焊縫軌跡切線方向大小不變,故有
(3)
(4)
(3)無側滑約束條件。機器人轉彎時若無側滑,則各輪沿機器人本體轉動半徑方向上的速度為0。以左側前輪為例有
(5)
其中,(xF,yF)為左側前輪中心點坐標。
機器人質心約束條件為
(6)
(4)由左前輪中心與H點幾何關系及式(6)可得
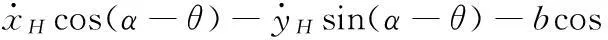
(7)
結合式(3)、式(4)可知,式(7)恒成立,說明該機構不存在滑移現象。
2.2四輪差速轉向移動機器人誤差模型
機器人差速轉向誤差模型如圖3所示:機器人質心的初始位置與水平線的夾角為θc,機器人下一個運動狀態時質心與水平線的夾角為θr,(xc,yc)是初始焊槍點的位置坐標,(xr,yr)為下一運動狀態時焊槍點的位置坐標,xe為當前時刻小車焊槍點相對上一時刻焊槍點在x方向的誤差,ye為當前時刻小車焊槍點相對上一時刻焊槍點在y方向的誤差。
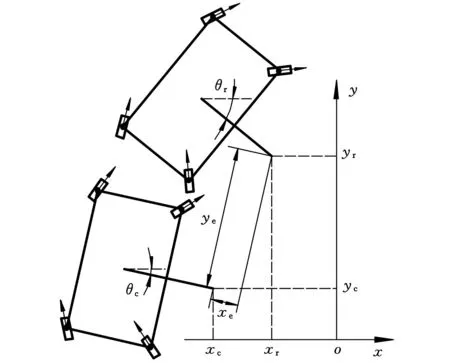
圖3 差速轉向誤差原理圖
由圖3得到機器人的誤差模型:
由文獻[8]可得機器人誤差微分方程:
3無側滑差速轉向運動仿真與分析
為驗證上述無側滑條件及差速轉向誤差模型的正確性,以機器人誤差模型為基礎對給定直角圓弧軌跡轉向進行數值仿真分析。仿真參數設定如下:vH=10mm/s,d=400mm,l=75mm,b=90mm,給定軌跡的直線距離a=1000mm;給定軌跡的圓弧半徑R0=800mm,如圖4所示。
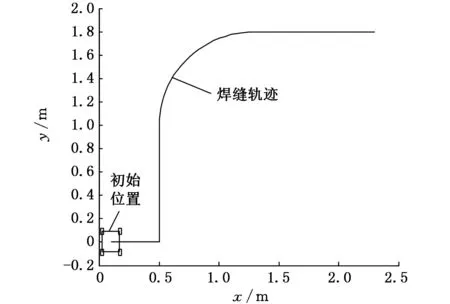
圖4 機器人的初始位置及焊縫軌跡
采用齊次坐標變換法,對機器人機構進行逆運動學求解,將機器人移動機構沿直線-圓弧-直線軌跡運動分解為第一段直線運動、圓弧運動及第二段直線運動,特別是在圓弧運動過程中通過運動學逆解求解出各驅動輪的角速度ω及偏轉角度θ。
運用MATLAB軟件對上述軌跡進行運動仿真,結果如圖5所示。機器人理論軌跡與仿真軌跡對比如圖6所示。
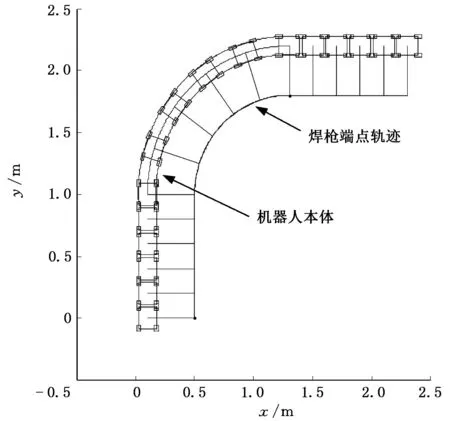
圖5 機器人的運動仿真過程
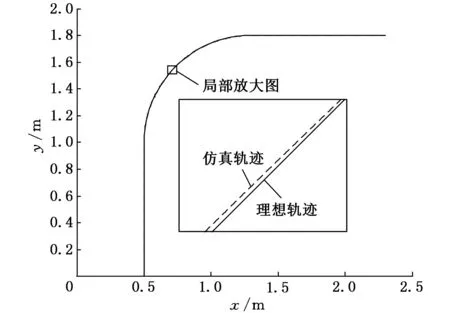
圖6 理論軌跡與仿真軌跡分析
機器人在運動仿真中經過圓弧后質心的坐標為(1299.90,2199.91)mm,理論坐標值為(1300,2200)mm,誤差為(-0.10,-0.09)mm。焊接點的坐標為(1299.77,1799.91)mm,理論坐標值為(1300,1800)mm,誤差為(-0.23,-0.09)mm。軌跡跟蹤后,得到焊槍到圓心的軌跡距離、轉動中心坐標及轉角的誤差。焊槍到圓心的距離為800mm,與設定的R0=800mm一致。轉動中心坐標為(-0.000 037,0.000 037)mm,轉角誤差為0.002 137°,仿真軌跡與理論軌跡基本重合。
仿真誤差的來源主要有:①機器人轉彎時前后輪轉向的角度分別為α和β,而在MATLAB仿真時對這兩個角度的初始值給定的精度可能不夠;②仿真僅考慮了運動學分析,未考慮到動力學特性,實際運動可能還要考慮慣性、偏心、摩擦等;③MATLAB軟件仿真時軟件本身產生的誤差等。
由上述分析可知,焊槍到圓心的距離誤差及轉角的誤差已基本消除,轉動中心的坐標誤差也在0.012mm以下,達到了焊接中的位置要求。仿真得出了機器人移動機構的運動軌跡,并將運動軌跡與目標軌跡進行了對比,得到了兩者的偏差,驗證了全輪差速轉向機構的運動精確性。
4結論
(1)對提出新型四輪驅動全輪差速轉向移動
機器人,采用非完整約束法建立了機器人的運動學模型,證明其滿足無側滑轉向時的約束條件。
(2)建立了該機器人機構的運動學誤差模型,采用MATLAB軟件以典型直線-圓弧-直線焊縫軌跡為例進行數值仿真,得到其轉角誤差為0.002 137°,轉動中心的坐標誤差小于0.012mm,驗證了其運動學及誤差模型的精確性,為該機構的進一步分析及控制提供了依據。
參考文獻:
[1]李曉延,武傳松,李午申. 中國焊接制造領域學科發展研究[J].機械工程學報,2012,48(6):19-31.
LiXiaoyan,WuChuansong,LiWushen.StudyontheProgressofWeldingScienceandTechnologyinChina[J].JournalofMechanicalEngineering, 2012,48(6):19-31.
[2]張軻,呂學勤,吳毅雄. 移動焊接機器人的研究現狀及發展趨勢[J]. 焊接,2004(8):5-9.
ZhangKe,LüXueqin,WuYixiong.ResearchStatusandDevelopmentTrendaboutMobileWeldingRobots[J].Weling&Joining, 2004(8):5-9.
[3]朱磊磊,陳軍. 輪式移動機器人研究綜述[J].機床與液壓,2009,37(8):242-247.
ZhuLeilei,ChenJun.AReviewofWheeledMobileRobots[J].MachineTool&Hydraulics, 2009,37(8),242-247.
[4]黃孝奎. 四輪轉向汽車控制研究及動力學仿真[D].沈陽:東北大學,2008.
[5]FischerW,TacheF,SiegwartR.MagneticWallClimbingRobotforThinSurfaceswithSpecificObstacles[C]//6thInternationalConferenceonFieldandServiceRobotics.Chamonix,2007:1-8.
[6]楊樹風.帶有機械臂的全方位移動機器人的研制[D].哈爾濱, 哈爾濱工業大學,2008.
[7]毛志偉,周少玲,石志新,等. 移動焊接機器人四輪驅動差速轉向方法:中國,102991578.A[P].2013-03-27.
[8]AngelesJ.機器人機械系統原理:理論、方法和算法[M]. 宋偉剛,譯. 北京:機械工業出版社,2004.
(編輯王旻玥)
收稿日期:2015-09-01
基金項目:國家自然科學基金資助項目(51265036)
中圖分類號:TH242
DOI:10.3969/j.issn.1004-132X.2016.13.006
作者簡介:毛志偉,男,1969年生。南昌大學機電工程學院副教授。主要研究方向為焊接自動化與機器人。發表論文30余篇。吳訓,男,1990年生。南昌大學機電工程學院碩士研究生。周少玲,女,1968年生。江西工業職業技術學院副教授。李向春,男,1990年生。南昌大學機電工程學院碩士研究生。鄧凡靈,男,1990年生。南昌大學機電工程學院碩士研究生。
Kinematics Analysis and Simulation for Four Wheel Drive All WheelDifferential Steering Mobile Welding Robots
Mao Zhiwei1Wu Xun1Zhou Shaoling2Li Xiangchun1Deng Fanling1
1.Nanchang University, Nanchang, 330031 2.Jiangxi Industry Polytechnic College, Nanchang, 330095
Abstract:In order to raise the stabilization,load capacity of mobile welding robots and to reduce the control complexity,a four wheel drive all wheel differential steering mobile welding robot mechanism was proposed.The differential steering principles of this mechanism were introduced and proved this mechanism had no sideslip.The differential steering deviation model was built with nonholonomic constraint method.Based on this model,a numerical simulation analysis of straight-arc-straight trajectory was presented.As results,the rotation angle deviation is as 0.002 137° and the deviation of rotation center is under 0.012 mm.The simulation results indicate that the model satisfies the position accuracy requirements.
Key words:four wheel drive mobile robot;all wheel differential steering;kinematic model;numerical simulation

