純擬凸函數(shù)的KKT型最優(yōu)性條件

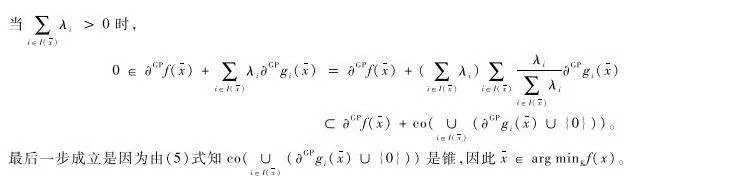
摘要：最優(yōu)性條件在優(yōu)化問題中起著非常重要的作用，尤其是對優(yōu)化算法的研究。但是在擬凸規(guī)劃的研究中，關(guān)于不可微擬凸規(guī)劃的KarushKuhnTukcer型（KKT型）最優(yōu)性條件的研究比較少。文章研究了純擬凸函數(shù)的GreenbergPierskalla次微分（GP次微分）和下全局次微分之間的關(guān)系，并且在此基礎(chǔ)上基于下全局次微分和GP次微分刻畫了一些純擬凸函數(shù)的KKT型最優(yōu)性條件。

關(guān)鍵詞：最優(yōu)性條件；擬凸規(guī)劃；全局次微分；GreenbergPierskalla次微分；下水平集

中圖分類號：O224文獻標志碼：A文章編號：16735072（2025）02015606

KarushKuhnTukcer Type Optimality Conditionsfor Neatly Quasiconvex Function

LU Guangjing，YOU Manxue

（School of Mathematics amp; Information，China West Normal University，Nanchong Sichuan 637009，China）

Abstract：Optimality conditions play a very important role in optimization problems，especially for optimization algorithms.However，in the study of quasiconvex programming，there is little research on the KarushKuhnTukcer type （KKT type） optimality conditions for nondifferentiable quasiconvex programming.In this paper，we study the relationship between GreenbergPierskalla subdifferential （GP subdifferential） and lower global subdifferential of neatly quasiconvex function，and characterize some KKT type optimality conditions for neatly quasiconvex function based on lower global subdifferential and GP subdifferential.

Keywords：optimality condition；quasiconvex programming；global subdifferential；GreenbergPierskalla subdifferential；sublevel set

由于擬凸性在經(jīng)濟學、圖像處理、機器學習等科學技術(shù)領(lǐng)域的廣泛應用，擬凸規(guī)劃的理論和數(shù)值研究成為優(yōu)化的前沿課題［13］。但是擬凸函數(shù)存在局部最小值不一定是全局最小值的問題，這導致在許多情況下擬凸問題處理難度大，因此研究者在擬凸函數(shù)的基礎(chǔ)上添加了一些假設(shè)以保證局部最小值是全局最小值，其中AlHomidan等［4］定義了一類能夠保證局部最小值是全局最小值的新函數(shù)，稱為純擬凸函數(shù)。擬凸函數(shù)還存在不一定可微的問題，所以研究者引入了一些方向?qū)?shù)及其次微分的概念［57］，并在此基礎(chǔ)上研究了擬凸規(guī)劃的最優(yōu)性條件，然而關(guān)于不可微擬凸規(guī)劃的KarushKuhuTukcer型（KKT型）最優(yōu)性條件的研究并不多，特別是對于純擬凸函數(shù)的KKT型最優(yōu)性條件研究。

參考文獻：

［1］SUZUKI S.KarushKuhnTucker type optimality condition for quasiconvex programming in terms of GreenbergPierskalla subdifferential［J］.Journal of Global Optimization，2021，79：191202.

［2］KABGANI A.Characterization of nonsmooth quasiconvex functions and their GreenbergPierskallas subdifferentials using semiquasidifferentiability notion［J］.Journal of Optimization Theory and Applications，2021，189（2）：666678.

［3］AGRAWAL A，BOYD S.Disciplined quasiconvex programming［J］.Optimization Letters，2020，14：16431657.

［4］AlHOMIDAN S，HADJISWAS N，SHAALAN L.Transformation of quasiconvex functions to eliminate local minima［J］.Journal of Optimization Theory and Applications，2018，177：93105.

［5］ANSARI Q H，LALITHA C S，MEHTA M.Generalized convexity，nonsmooth variational inequalities，and nonsmooth optimization［M］.Boca Raton：CRC Press，2013.

［6］CROUZEIX J P，LEGAZ J E M，VOLLE M.Generalized convexity，generalized monotonicity：recent results［M］.Boston：Springer，1998.

［7］LARA F，KABGANI A.On global subdifferentials with applications in nonsmooth optimization［J］.Journal of Global Optimization，2021，81：881900.

［8］KABGANI A，LARA F.Semistrictly and neatly quasiconvex programming using lower global subdifferentials［J］.Journal of Global Optimization，2023，86：845865

［9］SUZUKI S，KUROIWA D.Characterizations of the solution set for quasiconvex programming in terms of GreenbergPierskalla subdifferential［J］.Journal of Global Optimization，2015，62（3）：431441.

［10］梅家騮.廣義凸集的切錐［J］.南昌大學學報（理科版），1990，14（4）：2430.

［11］ROCKAFELLAR R T.Convex analysis［M］.Princeton：Princeton University Press，1997.

［12］LARA F.Optimality conditions for nonconvex nonsmooth optimization via global derivatives［J］.Journal of Optimization Theory and Applications，2020，185（1）：134150.

［13］GREENBERG H J，PIERSKALLA W P.Quasiconjugate functions and surrogate duality［J］.Cahiers du Centre détude de Recherche Operationelle，1973，15：437448.

［14］趙丹，田倍昕，游曼雪.利用GreenbergPierskalla次微分研究半無限擬凸規(guī)劃的KarushKuhnTucker條件［J］.西華師范大學學報（自然科學版），2021，42（4）：361366.