大排量離心泵固液兩相流磨損特性仿真分析

摘"" 要：針對大排量混砂離心泵，采用CFD-DEM耦合計算方法建立固液兩相流仿真模型，對離心泵內兩相流流場進行了研究。得到了不同葉輪轉速、流量、顆粒粒徑和混砂濃度等因素對離心泵外特性的影響。使用OKA、Archard磨損模型計算得到蝸殼及葉輪的磨損量，分析不同工況下顆粒運動過程及顆粒對過流部件的定性定量的磨蝕規律，得到平均磨損率隨時間變化曲線，并對不同鍍層的離心泵進行數值計算。結果表明，葉輪主要磨損區在根部和壓力面中部，轉速每增加100 r/min，最大磨損量為葉輪沖擊磨損，增加28.5%;流量增加20%，最大磨損量為蝸殼的沖擊磨損，增加85%。使用碳化鎢鍍層，葉輪和蝸殼磨損速率分別降低28.1%和39.95%。研究結果可為混砂離心泵參數設計提供指導意義。

關鍵詞：混砂離心泵;CFD-DEM;磨蝕規律;鍍層

中圖分類號：TE934.2"""""""" 文獻標志碼：A"""""" doi：10.3969/j.issn.1001-3482.2025.01.008

收稿日期： 2024-08-19

基金項目： 中國石油天然氣集團公司“十四五”前瞻性基礎性重大科技項目“大功率智能電驅壓裂裝備關鍵技術研究”（2022DJ4507）。

作者簡介： 彭俊威（1985-），男，高級工程師，碩士研究生，從事鉆井壓裂新備技術研究工作，E-mail：2005pjw@163.com。

Simulation Analysis of The Wearing Characteristics of Solid-Liquid Two-Phase Flow in Centrifugal Pumps

PENG Junwei1，2，ZHOU Qing 1，2，GENG Peng3，DONG Fuqiang1，2，SUN Tianhui4，DENG Wei1，2，LI Sen1，2

（1.CNPC National Petroleum Drilling Equipment Engineering Technology Research Center Company Limited， Baoji 721002，China ; 2. CNPC Baoji Oifield Machinery Co.，Ltd.， Baoji 721002，China; 3.Xi’an Branch，China Petroleum Materials Company Limited ， Xi’an 710018，China;4.China University of Petroleum， Beijing 102249，China）

Abstract： In order to establish a solid-liquid two-phase flow simulation model for the" large-displacement sand mixing centrifugal pump， a CFD-DEM coupling calculation method was employed. As a result， the two-phase flow field within the centrifugal pump was subsequently studied. The impact of varying impeller speed， flow rate， particle size， and sand mixing concentration on the external characteristics of the centrifugal pump was determined. Additionally， the wearing of the volute and impeller was calculated using the OKA and Archard wear models. The qualitative and quantitative abrasion laws governing particle movement and particles on the overflow parts under different working conditions were analyzed. The average wearing rate variation curve with time was obtained， and the centrifugal pumps with different coatings were numerically calculated. The findings indicated that the predominant areas of impeller wear were located at the root and the midpoint of the pressure surface. For each 100 r/min increase in speed， there was a corresponding increase in wear due to impeller impact， which increased by 28.5%. Additionally， there was a 20% increase in flow rate， and the maximum wear amount was the impact wear of the volute， which increased by 85%. The application of a tungsten carbide coating resulted in a reduction in the wear rates of the impeller and volute by 28.1% and 39.95%， respectively. This finding provides valuable insight that can inform the design of sand-mixing centrifugal pumps.

Key words： sand-mixing centrifugal pump; CFD-DEM; abrasion laws; coating

文章編號：1001-3482（2025）01-0044-09

大排量混砂離心泵作為壓裂液輸送設備，在油田的壓裂作業中起到重要作用[1-2]。壓裂作業環境為固液兩相流工況，壓裂液攜帶大量支撐劑固體顆粒，運行環境惡劣。內部葉輪、蝸殼等長期遭受堅硬固體顆粒的沖刷，水力部件壁面磨損嚴重，從而導致泵水力性能明顯下降，輸送系統壽命遠小于預期[3-4]。

為降低固液兩相流工況下的離心泵磨蝕，國內外學者展開了深入研究。其中數值模擬法具有邊界條件容易控制、耗費少、節約成本，用時短等優點，并且可反復模擬，優化設計的過程也相對簡單。因此在水力機械的研究中數值模擬有著重要的價值。目前對固液兩相流的數值模擬方法分為雙流體法和離散相法。

雙流體法是將固體顆粒視為與液體相同的連續介質。其中，趙斌娟等[5]研究顆粒在離心泵內的分布規律，研究表明隨著粒徑的減小，顆粒逐漸從葉片壓力面向吸力面流動。Yifang等[6]研究了離心泵內顆粒的分布規律，結果表明隨著顆粒體積分數增大，顆粒逐漸向葉片吸力面聚集。程效銳等[7]對雙吸離心泵的磨損特性進行了研究，結果表明增大粒徑會增加磨損，顆粒質量濃度影響大于顆粒直徑影響，且質量濃度變化會導致磨損位置的變化。廖姣[8]對粒徑0.05 mm，體積分數為10%的顆粒下工況進行了仿真分析，結果表明分流葉片可以減小葉片出口處的壓力脈動，減少顆粒聚集現象的產生，減輕葉片出口處的摩擦。

離散相法是在拉格朗日坐標系中采用獨立的方程來求解固相的運動，其中DEM法通過軟球模型計算顆粒的運動，能準確模擬固液兩相流工況下離心泵內顆粒的運動。Kafui[9]提出將DEM與CFD進行耦合計算，以提高計算效率，擴展了其在兩相流領域內的應用范圍。Tang等[10]采用CFD-DEM耦合方法研究了離心泵內固體顆粒的運動特性，結果表明小顆粒具有較寬的速度范圍和速度峰值，而大顆粒具有較大的接觸力，餅狀顆粒的接觸次數最多，球形顆粒的接觸次數最少。黃凱[11]使用CFD-EDM耦合方法，監測過流部件的磨損率和顆粒的運動，發現隨著質量濃度的增加，揚程和效率減小，葉輪的磨損率增大，葉片比前后蓋板更易被磨損，葉片的磨損區域由點狀衍變為片狀。王田田等[12-13]對球形、類球形、三角形三種顆粒在不同粒徑（1～3 mm）、體積分數（2%～4%）下進行了仿真計算，結果表明顆粒直徑增大，葉片磨損增加，磨損位置逐漸向葉片頭部轉移，顆粒體積分數增加，磨損位置不變，磨損程度增大，顆粒尖銳程度增大也會加劇磨損。

現今中外學者借助兩相流理論和經驗模型，開展對于不同規格離心泵磨損特性的研究，通過固液兩相流場分析磨損機理[14-15]，但針對大排量高砂比泵的相關研究較少。本文使用CFD-DEM耦合計算的方法，針對石油行業的大排量混砂離心泵長期遭受堅硬固體顆粒沖刷的環境下，開展對固液兩相流高砂比工況離心泵磨損機理的研究，研究離心泵性能和磨損趨勢變化，指導大排量混砂設備離心泵設計，提升壽命和經濟性選型。

1 CFD-DEM兩相流計算模型

1.1 數學模型

壓裂液作為不可壓縮流體，在數值模擬過程中要保證質量守恒和動量守恒。連續性方程描述了流體質量守恒的關系，即在單位時間內流入單位體積的質量等于流出單位體積的質量，公式為：

+?·（ρ[→][v]）=Sm（1）

動量守恒方程描述了兩相流體在流動中的力學特性，包括流體的速度分布、流速和流動阻力等，公式為：

（ρ[→][v]）+?·（ρ[→][v][→][v]）=-?p+?·（[=][τ]）+ρ[ɡ][-]+[→][F]（2）

式中：p為靜壓，[=][τ]為應力張量，ρ[ɡ][-]為自重，[→][F]為相互作用力。

CFD-DEM耦合借助Fluent中的DDPM模型實現。其質量守恒和動量守恒方程基本假設是在顆粒離散相體積分數足夠低情況，公式為：

"""""" +?·（ρ[→][v]）=SDPM + Sother（3）

+?·（ρ[→][v][→][v]）=-?p+?·τ+ρ[ɡ][→]+

"""" [→][FDPM] +[→][Fother]（4）

式中：ρ為連續相密度，kg/m3;[→][v]為連續相速度矢量，m/s;SDPM和Sother為DPM離散相及其他附加的質量源項，kg/（m3·s）;ρ[ɡ][→]為重力，N/m3;[→][FDPM] 和[→][Fother]為DPM離散相及其他附加的體積力，N/m3。

混砂離心泵工作時固相體積分數較高，為了克服上述方程限制，引入拓展體積分數p解釋顆粒相：

（αpρp）+?（αpρp[→][vp]）=[q=1][nphas][∑]（[m][.]qp-[m][.]pq）（5）

（αpρp[→][vp]）+?（αpρp[→][vp][→][vp]）=

αpρp[ɡ][→]+Fvm，lift，user-αp?p+?·[αpμp（?[→][vp]+?[→][vp][T]）]+

KDP（[→][v]DPM - [→][vp]）+SDPM，explicit+

[q=1][nphas][∑]（[→][K]qp（[→][vq]-[→][vp]）-[m][.]qp[→][v]pq+[m][.]pq[→][v]pq）（6）

式中：αp為p相體積分數;ρp為p相密度，kg/m3;μp為p相黏度，kg/m2·s;[→][vp]和[→][vq]分別為p相和q相速度矢量，m/s;[→][v]pq為兩相相對速度，m/s;[m][.]qp和[m][.]pq為p相和q相之間的質量傳遞，kg/（m3·s）;Fvm，lift，user為虛擬質量力、升力及其他作用力的合力，N/m3;[→][v]DPM表示離散相顆粒的平均速度，m/s;[→][K]qp和KDPM分別為相間動量交換系數和顆粒動量變換系數;SDPM，explicit為DPM顯式質量源項，kg/（m3·s）。

顆粒的碰撞模型采用Hertz-Mindlin無滑移接觸模型，施加在顆粒上的法向力Fn模型由法向接觸力和阻尼力組成，為法向重疊量δn的函數：

"""""""""""""""" Fn=Fcn+Fdn=Eδn （7）

其中：

"""""""""""""""" =+（8）

"""""""""""""nbsp;"" =（9）

式中：Fcn為法向接觸力;Fdn為法向阻尼力;E為等效彈性模量;R為等效顆粒半徑;E1、E2分別為兩顆粒的彈性模量;R1、R2分別為兩顆粒的接觸半徑。

法向力中阻尼力Fdn表達式為：

Fdn=-2β（10）

其中：

Fdn==（11）

Fdn=β=（12）

Fdn=Sn=2E（13）

式中：m*為當量質量;m1、m2分別為兩顆粒的質量，kg;vn為相對速度的法向分量，m/s;e為恢復系數;Sn為法向剛度，N/m。

施加在顆粒上的切向力Ft由切向接觸力和阻尼力組成，為切向重疊量δt的函數：

Ft=Fct+Fdt=-St δt（14）

其中：

St=8G*（15）

式中：G*為當量剪切模量，MPa。

切向力中阻尼力Fdt表達式為：

Fdt=-2β（16）

式中：vt為相對速度的切向分量;St為切向剛度。

顆粒之間的摩擦力μSFn會影響切向力，其中μS為靜摩擦因數。

顆粒的滾動摩擦模型選擇標準滾動摩擦模型，該模型通過在接觸表面添加力矩考慮滾動摩擦情況：

τi=-μrFnRiωi（17）

式中：μr為滾動摩擦因數;Ri為顆粒質心與接觸點的距離;ωi是接觸點處的角速度。

本研究中使用OKA磨損模型計算顆粒對過流部件的沖擊磨損，使用Archard模型計算顆粒對過流部件的摩擦磨損。

OKA磨損模型由Oka和Yoshida在2005年提出。主要用于計算顆粒沖擊設備表面時發生的侵蝕性磨損。該模型通過顆粒尺寸、顆粒沖擊速度和顆粒沖擊角度等參數的函數關系預測了顆粒沖擊引起的體積損失。

DωA=ɡ（α）E（α）mp（18）

E（α）=65W-" （） （）0.19（19）

""" ɡ（α）=sin（α）"""""" C（α）（20）

C（α）=1+Hv（1-sin（α））（21）

式中：Dω為沖蝕深度，m;A為沖擊面積，m2;ɡ（α）為歸一化的沖蝕角函數;E（α）為單位質量下的磨損體積，m3;mp為顆粒質量，kg;W為材料磨損常數;v為顆粒的沖擊速度，m/s;Hv為材料的維氏硬度，GPa;D為顆粒直徑，m;k1為試驗推導的經驗系數，對于石英砂顆粒取0.12。sin（α）"""""" 計算由于重復變形引起的歸一化侵蝕;C（α）計算由于沖擊引起的材料移除過程。

Archard磨損模型由Archard于1940年提出。該公式通過考慮材料表面微觀突起和顆粒之間的接觸，描述了材料摩擦磨損程度與顆粒所作摩擦功之間的關系，方程定義為：

Q=WFndt（22）

W=K/Hv（23）

式中：Q為去除材料的體積，m3;Fn為顆粒沖擊力，N;dt為顆粒移動的切向距離，m;W為磨損常數;K為無量綱常數;Hv為材料的維氏硬度，GPa。

1.2 模型建立

本文以寶石機械355.6 mm×304.8 mm×558.8 mm大排量混砂離心泵為研究對象。該離心泵葉片為開式葉片，蝸殼為雙流道結構。設計最大流量Q=29 m3/min，額定轉速1 200 ～1 400 r/min，清水條件下額定輸入功率≥370 kW，吸入口通直徑355.6 mm，排出口通徑304.8 mm。

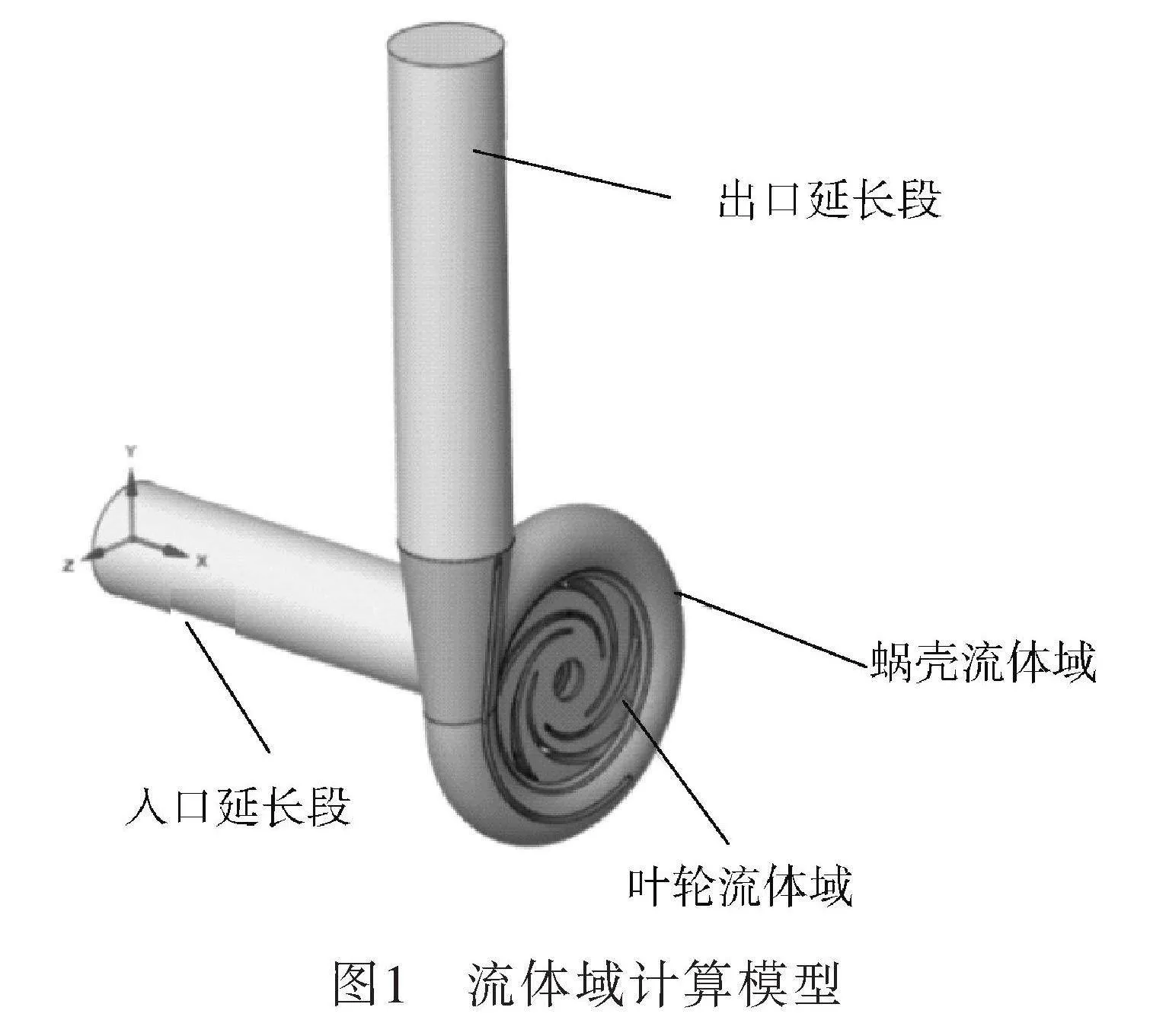
使用SpaceClaim對離心泵幾何模型進行簡化處理后進行流體域抽取，并添加入口延長段和出口延長段，得到最終的離心泵流體域模型如圖1所示。

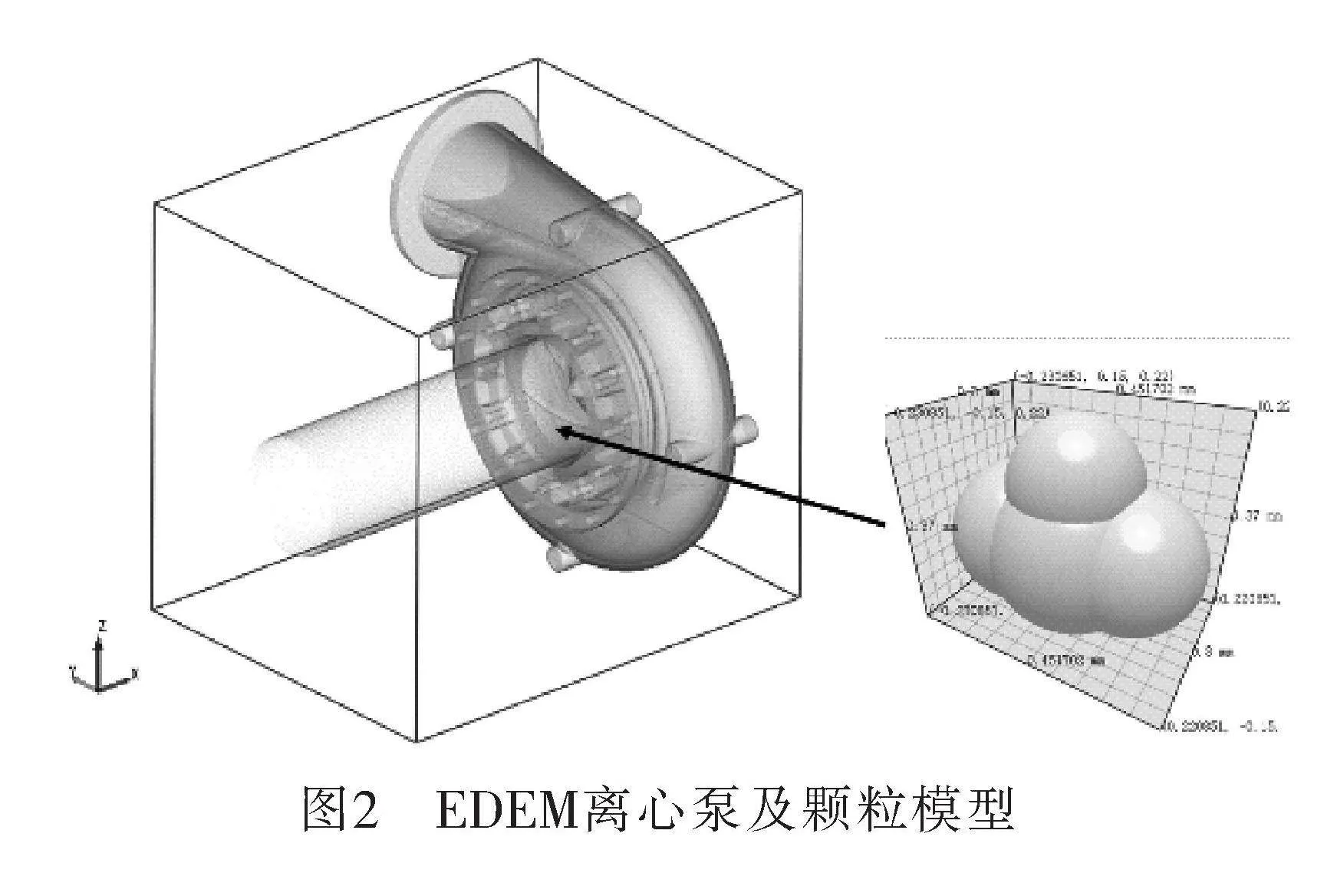
EDEM中導入簡化后的離心泵固體域模型，將顆粒工廠設置在入口延長段靠近葉輪處，防止顆粒生成時流出流體區域導致的計算發散。顆粒模型使用多個球形顆粒堆積模擬圓度為0.6的石英砂顆粒。EDEM中離心泵及顆粒模型如圖2所示。由于支撐劑顆粒體積較小，采用真實尺度對顆粒進行建模會導致顆粒數量龐大，大大降低了計算效率。因此在仿真中使用了曳力放大的方法，將顆粒直徑成倍數放大后，在Fluent中的流體作用力也成倍進行放大，使用大顆粒模擬多個小顆粒，降低顆粒個數提高計算效率。顆粒放大倍數根據不同工況進行調整。

1.2" 網格劃分

流體計算模型由入口延長段、葉輪流體域、蝸殼流體域、出口延長段四部分組成。為保證網格質量，縮短計算時間，本文采用六面體+多面體的方法進行劃分。流道中心區域使用規則的六面體網格，在壁面附近使用多面體網格以適應葉輪和蝸殼的曲面及倒角。模型網格劃分如圖3所示。

1.3 邊界條件

流體域模型入口為速度入口，出口為壓力出口。湍流模型采用k-ω SST模型[16]。各部分流體域之間通過Interface邊界連接，設置葉輪繞-x軸以恒定角速度旋轉。設置時間步長1.0×10-4 s。同時EDEM中設置葉輪初始相位與流體域相同，并添加葉輪部件以相同角速度運動。設置EDEM 時間步長為1.0×10-6 s。

仿真中壓裂液密度和黏度為1 000 kg/m3和40 mPa·s。支撐劑密度為2 650 kg/m3[17]。入口流速及顆粒生成速率根據工況條件進行調整。

1.4 模型驗證

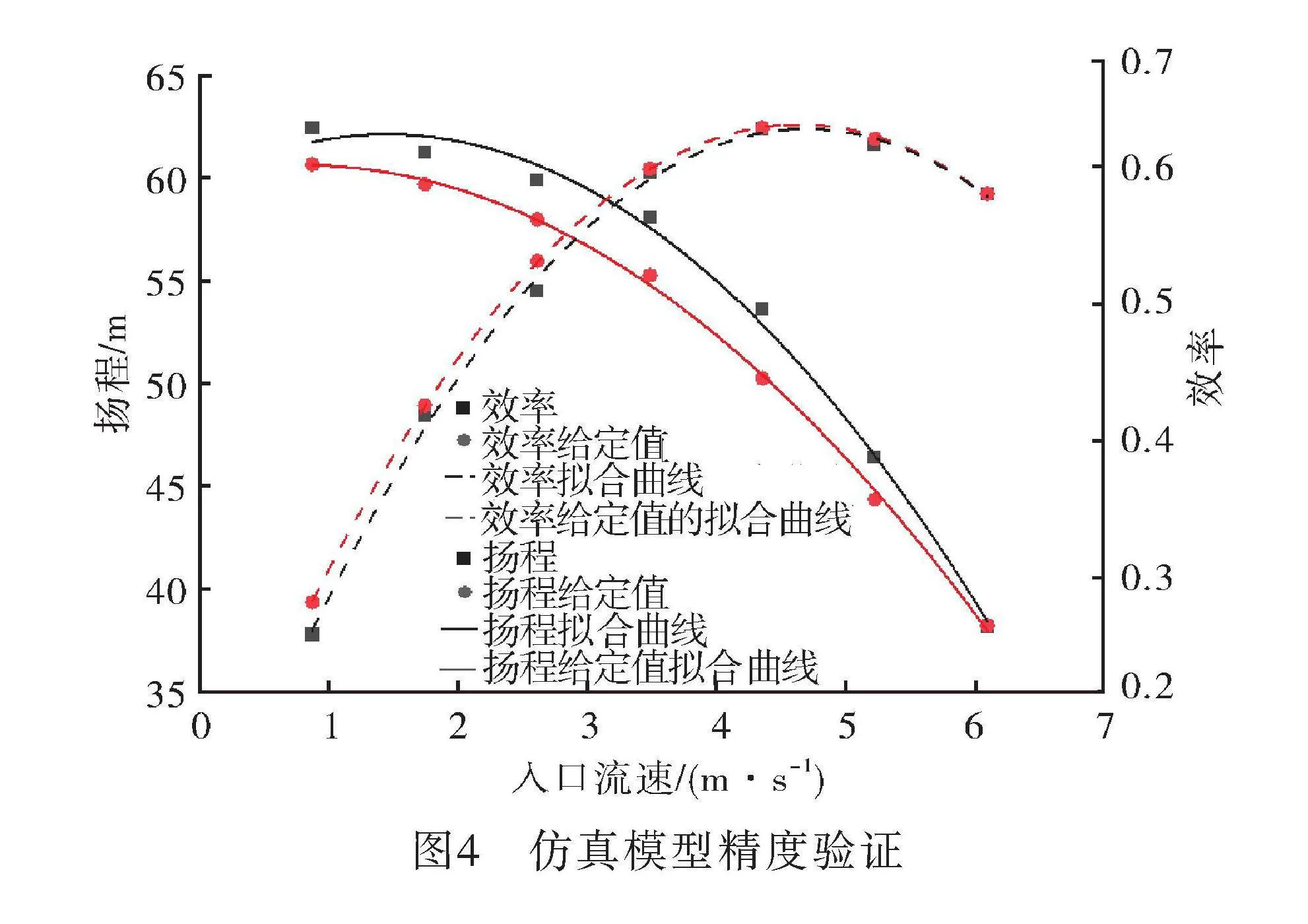
為驗證所建立的計算模型準確性，通過對離心泵手冊中的特性曲線進行處理，獲得清水工況下的離心泵外部特性曲線。在工作流量范圍內等差選取7組工況進行數值模擬，計算結果如圖4所示。在最大效率點附近（流量在15.14～22.71 m3/min），揚程及效率計算誤差均在10%以內，說明所建立得到計算模型滿足計算精度要求。

2 泵內顆粒運動過程分析

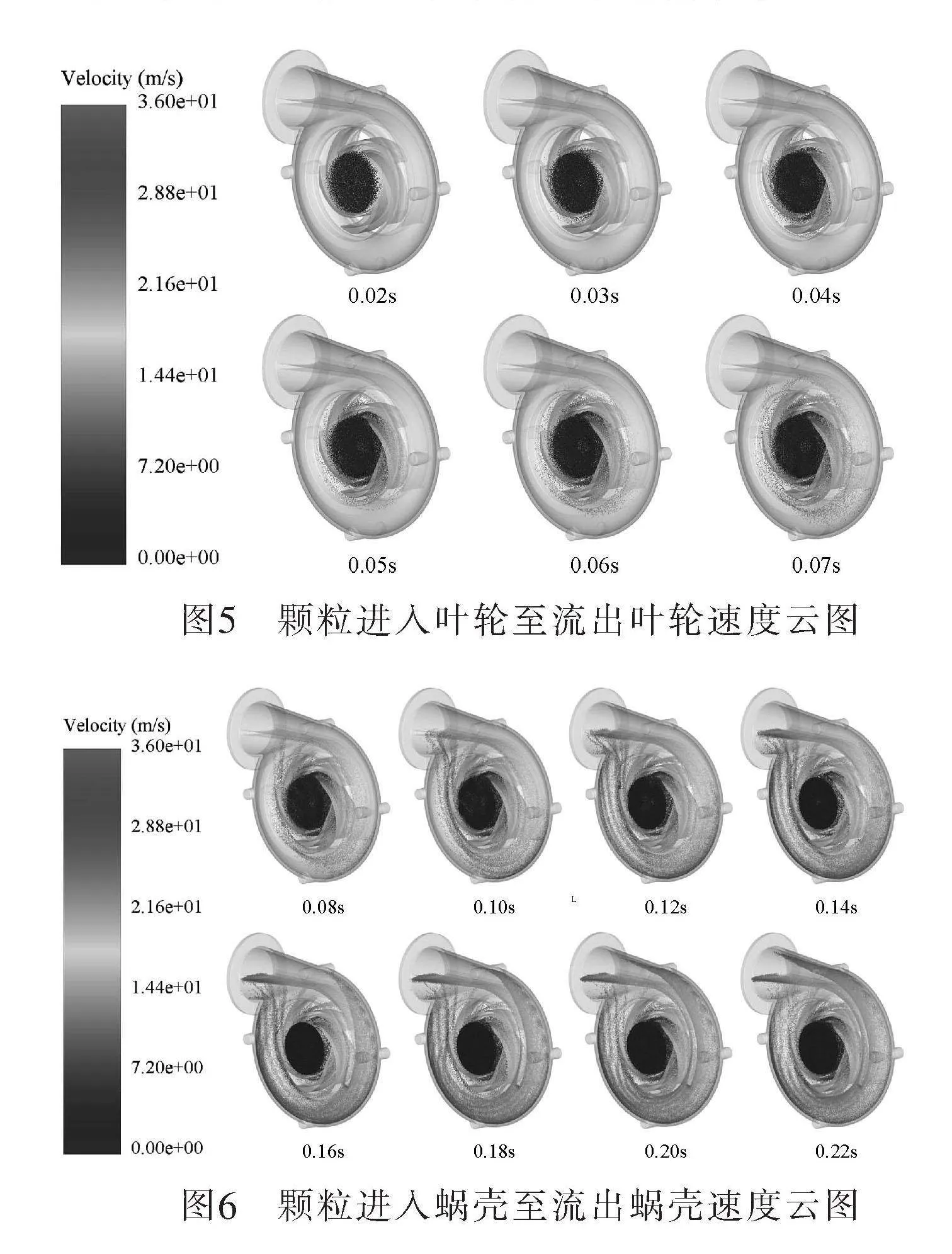
以流量18.92 m3/min、顆粒尺寸30目、顆粒體積分數10%、葉輪轉速1 200 r/min為例，提取顆粒進入至流出葉輪區域過程的顆粒運動速度分布云圖，如圖5所示。顆粒進入離心泵后0.03 s時，在離心力作用下快速向徑向擴散，主要包裹了葉輪靠近中心的葉片根部邊緣區域。0.05 s時顆粒運動到葉輪流道中部位置，此時葉輪壓力面根部部分位置與顆粒碰撞。顆粒進入離心泵后約0.07 s流出葉輪。

顆粒進入至流出蝸殼區域過程的顆粒運動速度分布云圖，如圖6所示。顆粒進入蝸殼后在慣性力作用下沿蝸殼流道內壁向出口運動。分隔板將蝸殼分為上下兩個流道。0.15 s時分隔板內側流道內顆粒運動已經基本達到穩定，此時外側顆粒運動至蝸殼增壓管根部附近。0.20 s后，蝸殼內部顆粒運動基本達到穩定。顆粒進入蝸殼后向外側偏移。

3 蝸殼及葉輪磨損研究

3.1 蝸殼及葉輪磨損區域

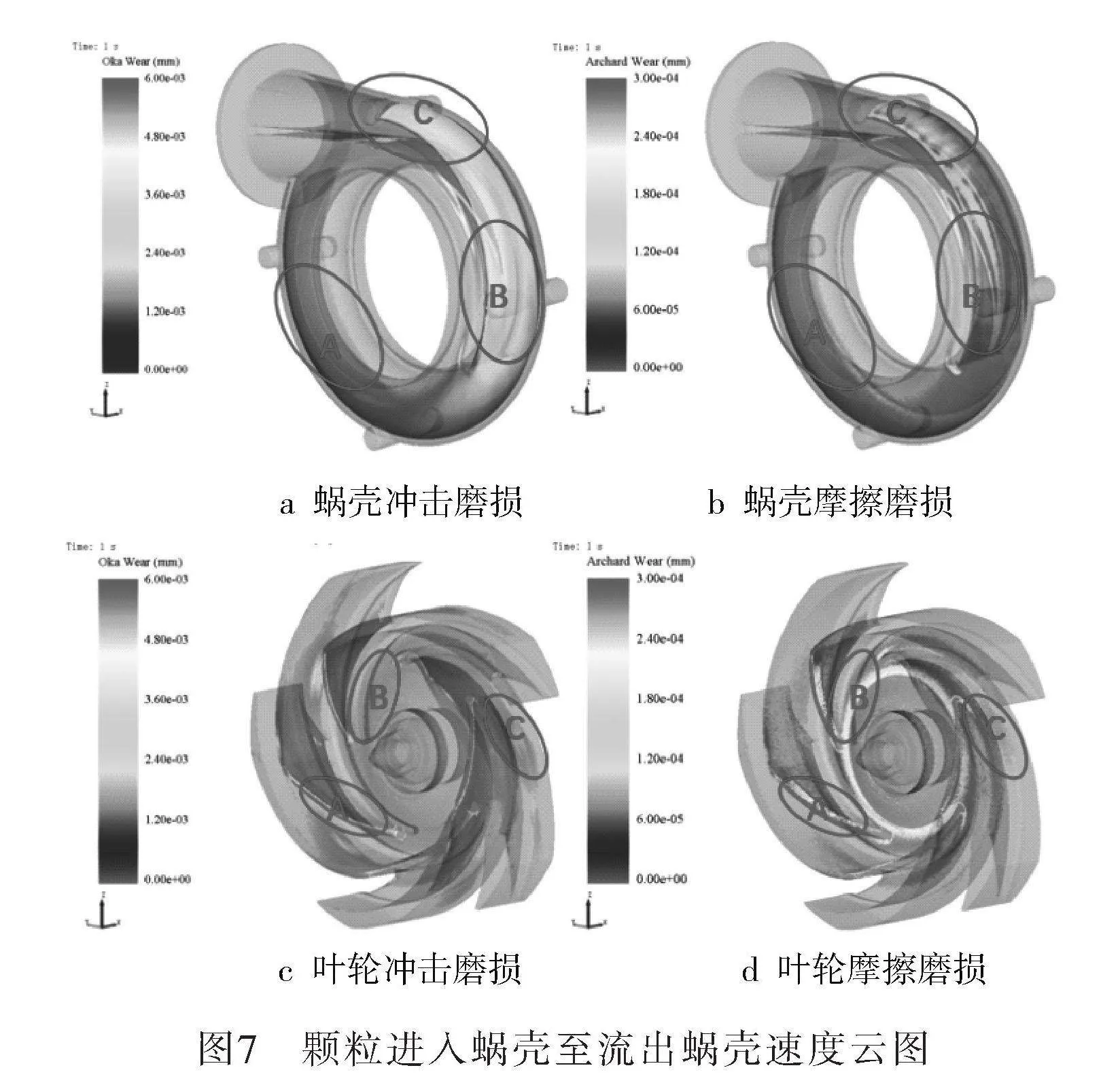
不同工況下的泵內顆粒運動規律及分布基本相同，以流量為18.92 m3/min、顆粒尺寸30目、顆粒體積分數10%、葉輪轉速1 200 r/min工況為例，提取了葉輪及蝸殼的摩擦磨損和沖擊磨損云圖如圖7所示。

蝸殼及葉輪表面磨損可分為三個區域。

蝸殼A區域為蝸殼內流道底部。該區域不存在分隔板，顆粒運動速度較低，摩擦磨損和沖擊磨損量均比較少;B區域為分隔板根部位置，從葉輪流出的高速顆粒在該位置向蝸殼內外兩個流道分散，主要產生沖擊磨損;C區域為蝸殼出口增壓管根部，分隔板上下兩個流道均出現磨損現象。由于分隔板下方流道的顆粒更靠近葉輪，運動速度更大，因此分隔板下方所受到的沖擊磨損和摩擦磨損相對于上方流道都更加嚴重。

葉輪A區域為葉片根部邊緣，由于顆粒進入離心泵時向軸向運動同時在離心力作用下向徑向擴散，因此該位置同時發生了比較嚴重的摩擦磨損和沖擊磨損。B區域為葉輪底面，顆粒進入葉輪區域后，軸向分速度逐漸降低，運動至葉輪底部時主要為離心力作用下產生的徑向速度，因此在底部主要發生摩擦磨損，沖擊磨損量很低。葉輪C區域為葉片壓力面中心區域，由于葉輪轉動至蝸殼隔水角附近時顆粒速度低，在該位置葉片更容易與顆粒發生碰撞，因此主要產生沖擊磨損。

3.2 不同條件蝸殼及葉輪磨損速率

不同轉速下蝸殼的沖擊磨損及摩擦磨損如圖8～9所示。在其他條件相同時，葉輪轉速的提高增加了蝸殼分隔板下表面的沖擊磨損以及蝸殼下方流道的摩擦磨損，主要磨損區域未發生明顯變化。

圖10為不同轉速下的蝸殼沖擊磨損量及摩擦磨損量隨時間變化曲線。在其他條件相同時，轉速每增加100 r/min時，蝸殼的沖擊磨損量和摩擦磨損量分別平均增加13%和18.5%。

不同轉速下葉輪的沖擊磨損及摩擦磨損如圖11～12所示。在其他條件相同時，葉輪轉速的對葉輪壓力面的沖擊磨損影響較大，同時葉輪底面所受的摩擦磨損量也呈上升趨勢。

圖13為不同轉速下的葉輪沖擊磨損量及摩擦磨損量隨時間變化曲線。葉輪轉速的增加使顆粒獲得了更大的動能，導致磨損更加嚴重。葉輪轉速的增加對葉輪的沖擊磨損影響更大。在其他條件相同時，轉速每增加100 r/min時，葉輪的沖擊磨損量和摩擦磨損量分別平均增加28.5%和8%。轉速主要影響了葉輪受到的沖擊磨損。

不同流量下蝸殼沖擊磨損及摩擦磨損如圖14～圖15所示。在其他條件相同時，流量的提高使得蝸殼所受摩擦磨損和沖擊磨損提高，主要磨損區域面

積增加，沖擊磨損和摩擦磨損范圍均向離心泵分隔板根尾部延伸。

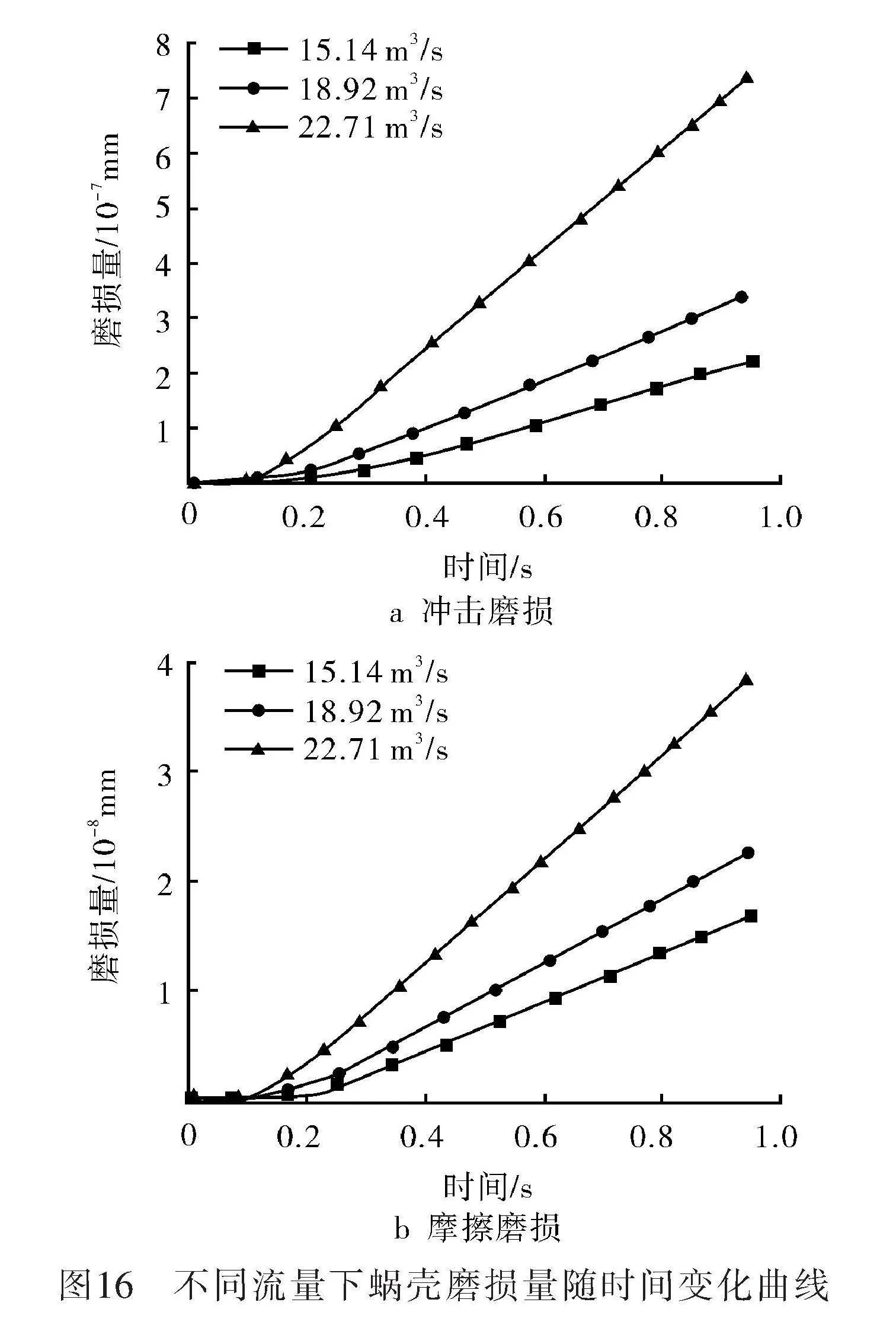
圖16為不同流量下的蝸殼沖擊磨損量及摩擦磨損量隨時間變化曲線。在其他條件相同時，入口流量每增加20%，蝸殼的沖擊磨損量和摩擦磨損量分別增加85%和53%。

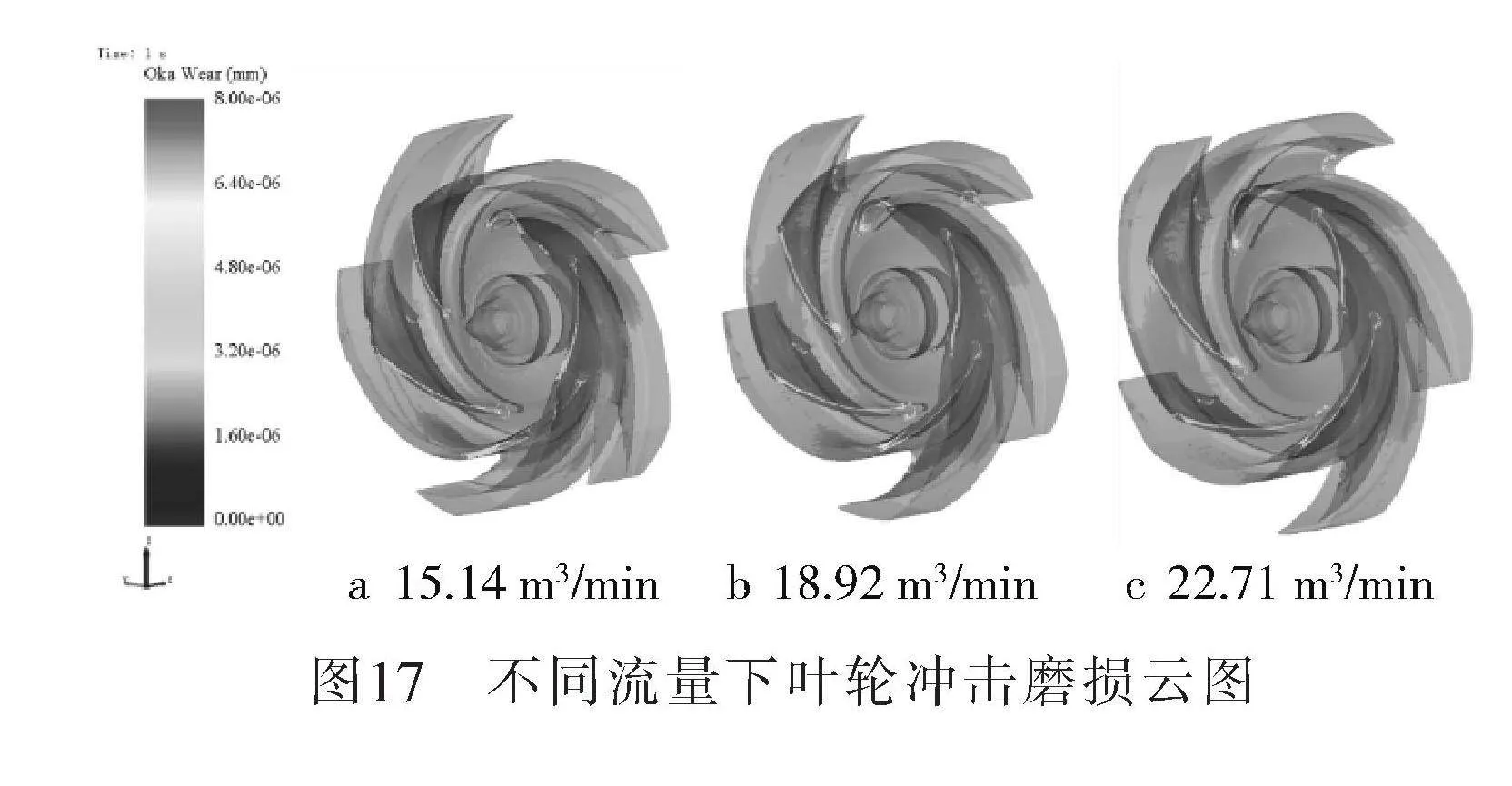
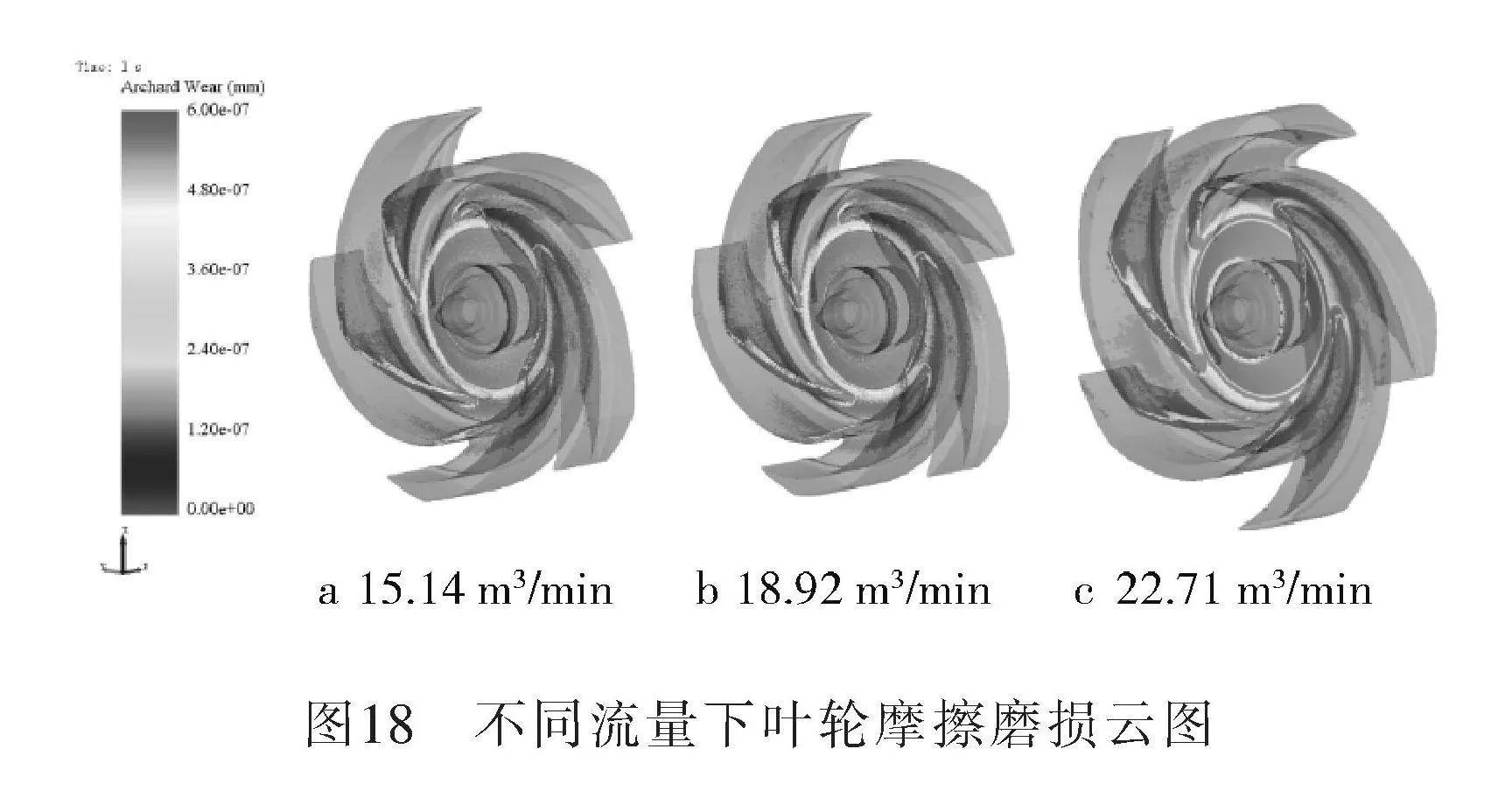
不同流量下葉輪沖擊磨損及摩擦磨損如圖17～18所示。在其他條件相同時，隨流量的提高葉輪主要沖擊磨損位置未發生明顯變化，葉片根部邊緣和底部所受的摩擦磨區域增加。

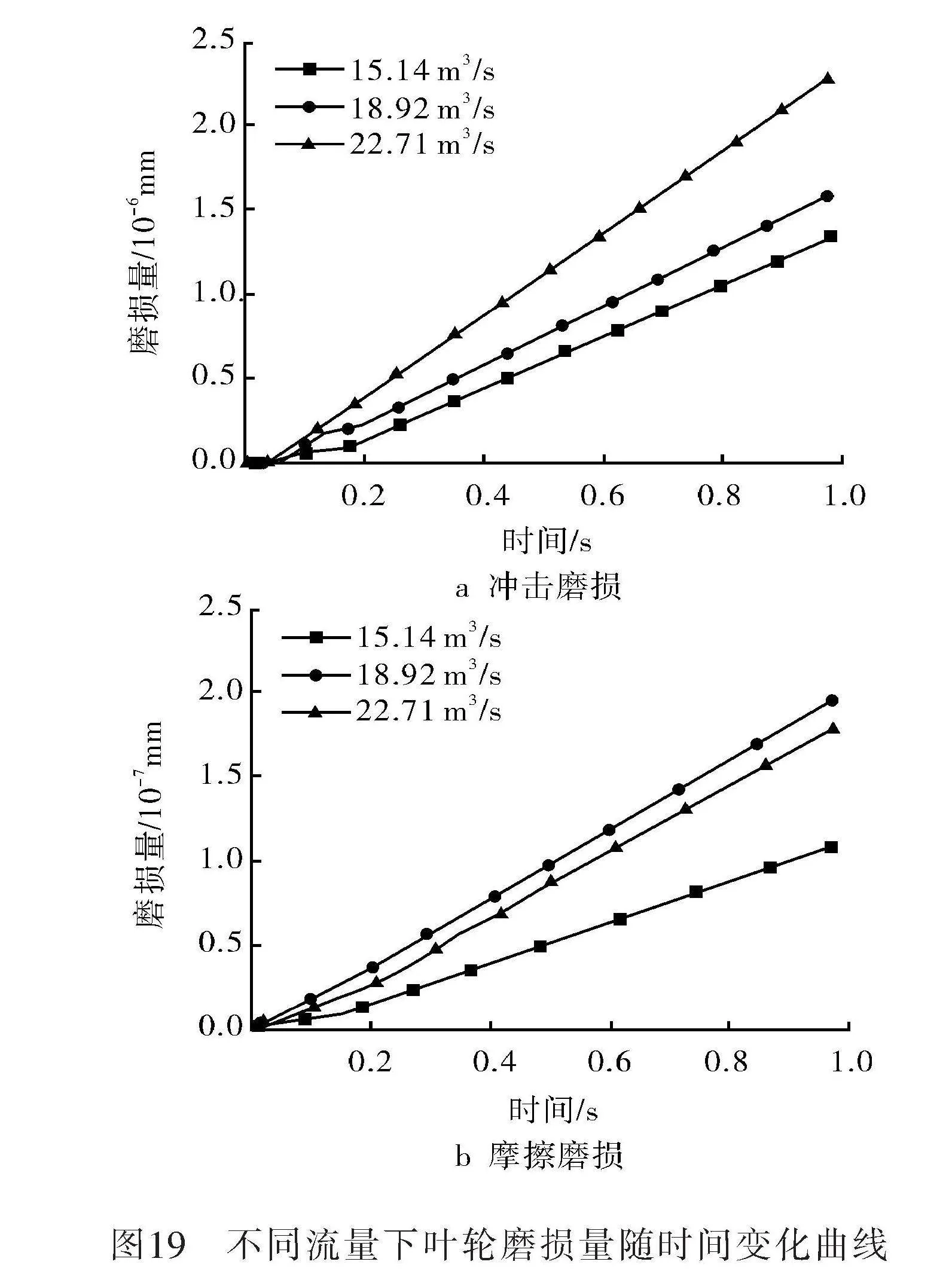
圖19為不同流量下的葉輪沖擊磨損量及摩擦磨損量隨時間變化曲線。在其他條件相同時，流量的增加使葉輪的沖擊磨損量上升幅度程增大趨勢、而摩擦磨損上升幅度減小。入口流量每增加3.785 m3/min，葉輪的沖擊磨損量和摩擦磨損量分別增加31.5%和38.5%。流量的增加對蝸殼的影響程度要大于對葉輪的影響程度。

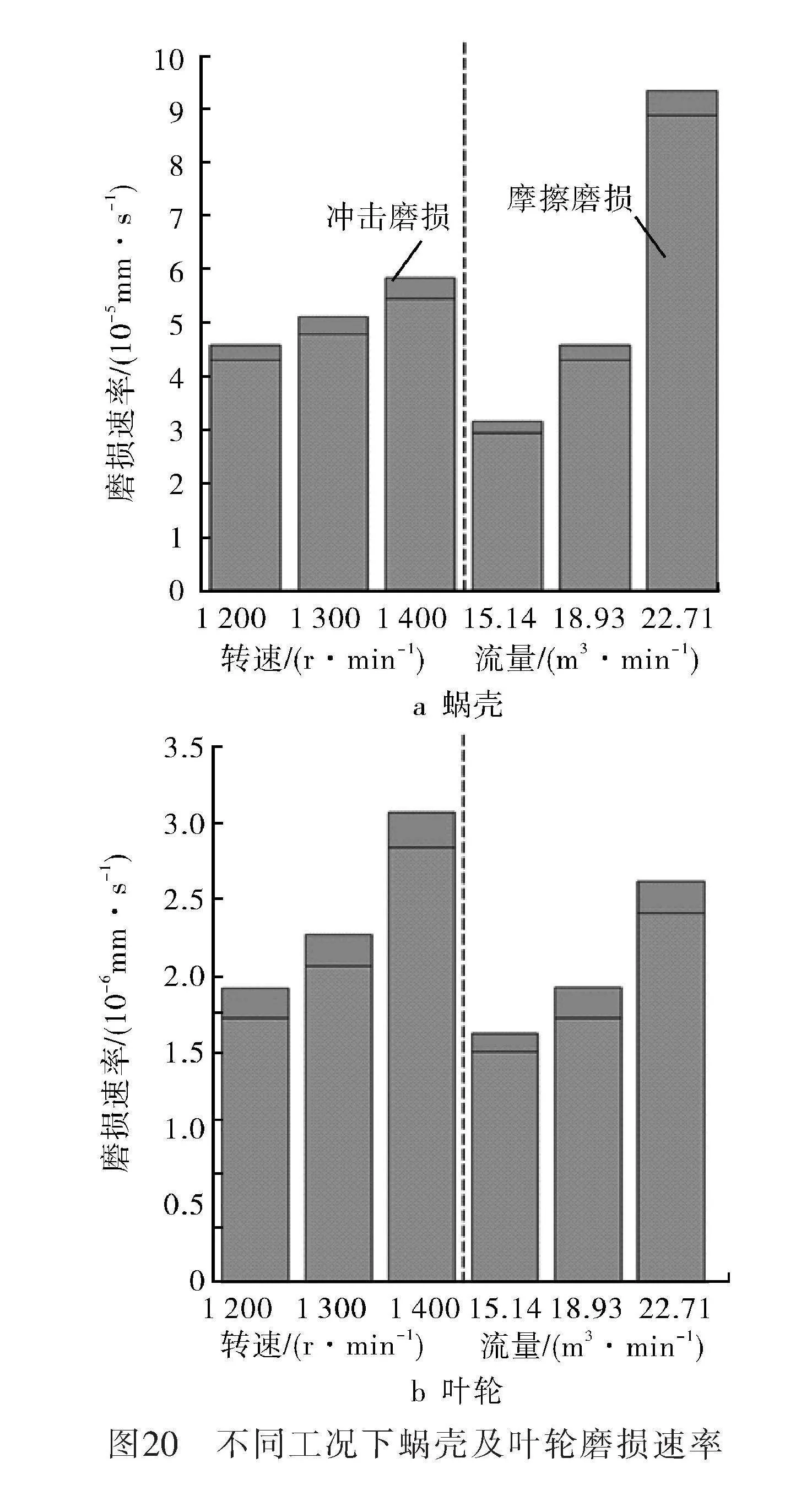
由上述結果可知，在離心泵運行0.3 s后，蝸殼及葉輪的磨損量基本呈線性增長趨勢。因此對0.3 s后磨損數據進行線性擬合處理，并將沖擊磨損量與摩擦磨損量進行疊加，得到不同工況下蝸殼和葉輪的總體磨損速率，如圖20所示。由圖20可知，蝸殼及葉輪主要受到沖擊磨損影響，相同條件下摩擦磨損速率比沖擊磨損速率小得多。蝸殼磨損速率主要受流量影響，葉輪磨損速率主要受轉速影響。同時葉輪的磨損量要比蝸殼大4至5倍。

4 不同鍍層對離心泵磨損的影響

由上可知，蝸殼與葉輪所受的沖擊磨損要大于摩擦磨損。根據式（14）～（17），對于大排量離心泵的顆粒磨損受以下因素影響：

1） 顆粒本身物理屬性，如質量、直徑。

2） 輸送參數引起的顆粒運動屬性，如顆粒運動速度、沖擊角度等。

3） 離心泵的材料屬性，如硬度及材料常數等。

顆粒本身物理屬性及輸送參數受離心泵作業指標影響。為降低磨損，考慮以更換鍍層的方式提高離心泵過流部件表面硬度，提高蝸殼及葉輪的使用壽命。

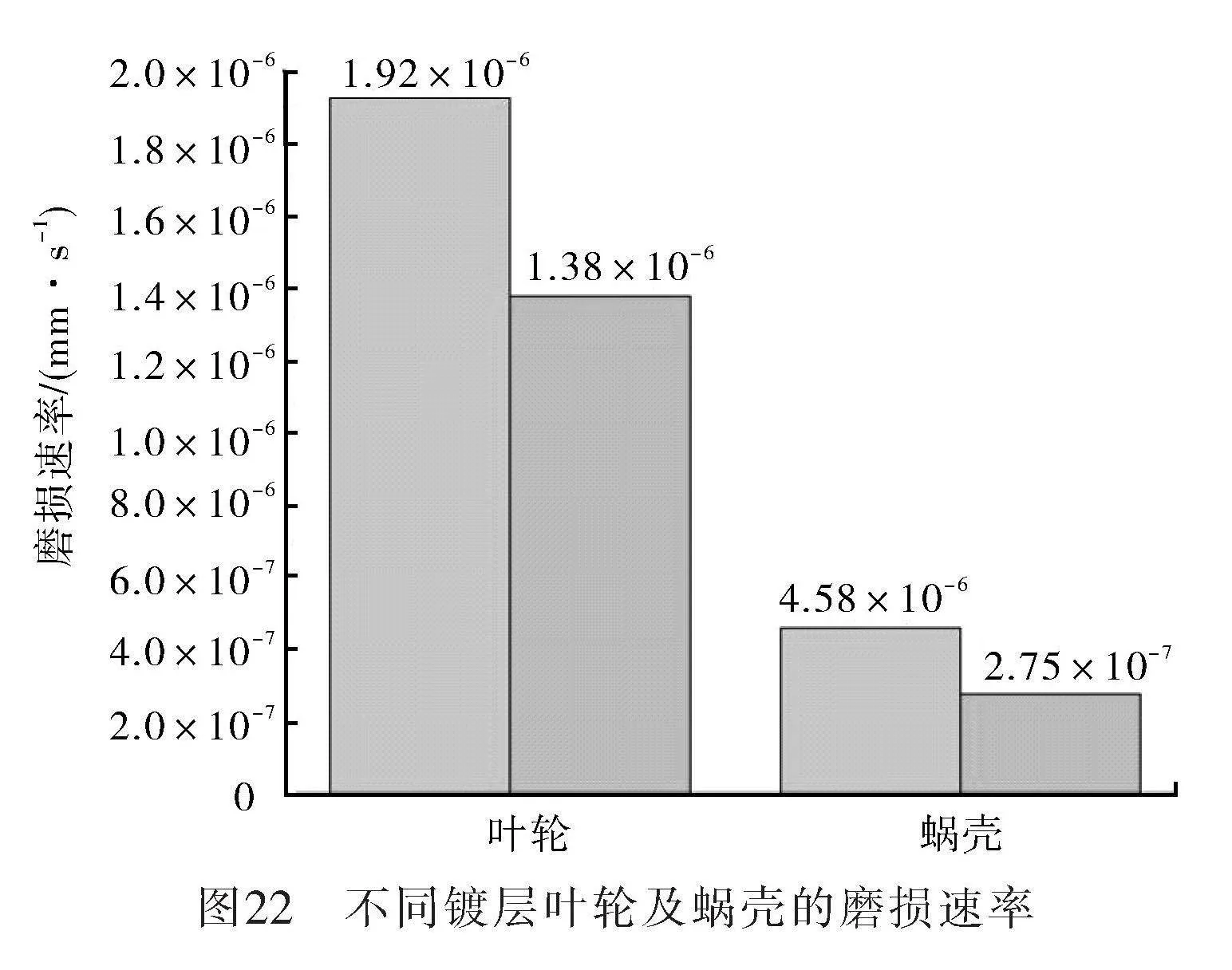
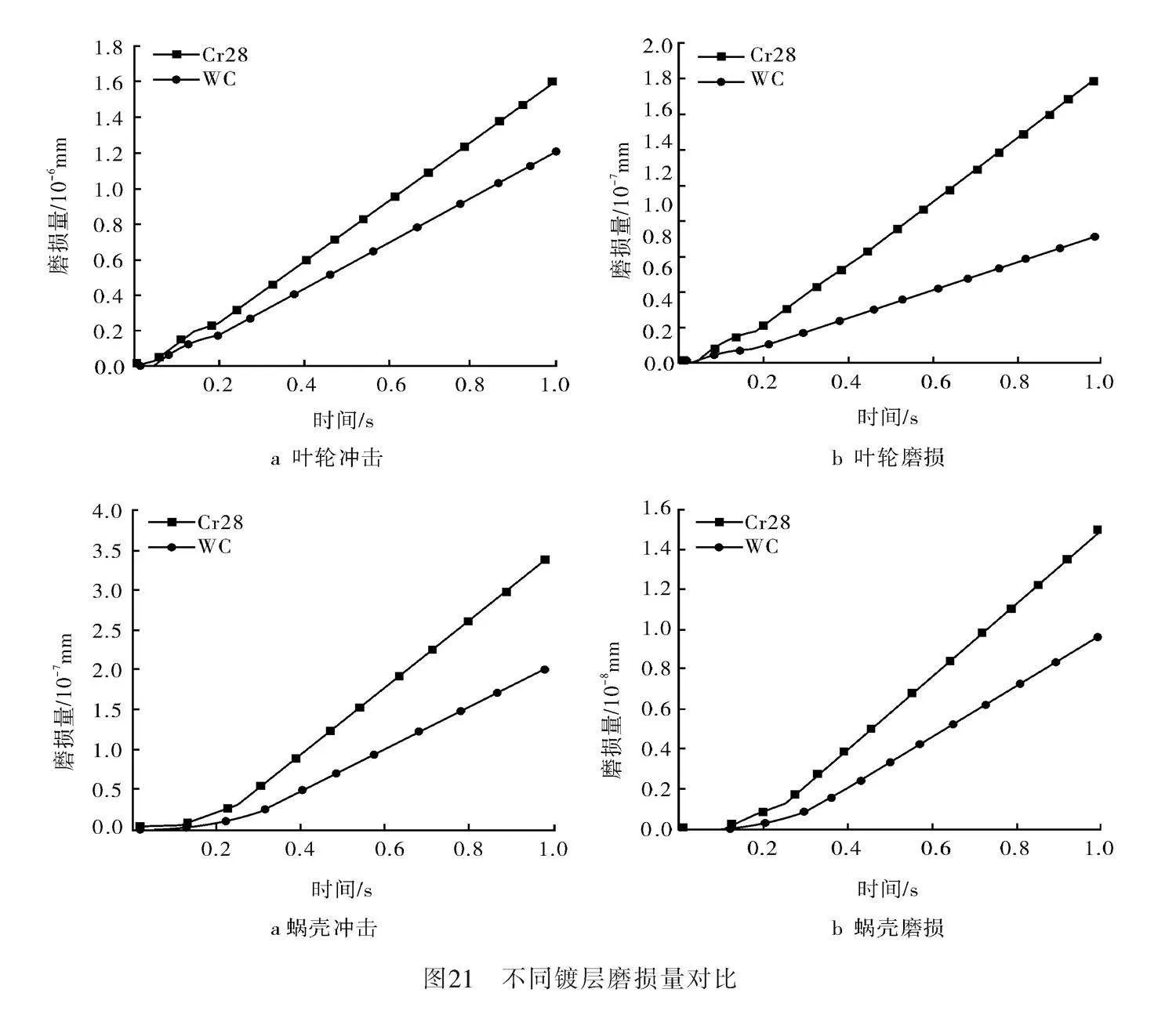
原離心泵材料為ASTM A532 Class Ⅲ Type A，采用高鉻合金Cr28。本身擁有良好的耐磨性能和耐腐蝕性能。為了增強其耐磨性能考慮在其表面增加碳化鎢涂層以提高耐磨性能。熱噴涂碳化鎢（WC）涂層硬度通常在1 200～1 600 HV之間，本研究中取1 400 HV。以流量為18.92 m3/min、顆粒尺寸30目、顆粒質量分數10%、葉輪轉速1 200 r/min工況為例，對比蝸殼及葉輪的磨損量以及磨損速率，如圖21～22所示。使用碳化鎢鍍層后，離心泵整體磨損量和磨損速率降低，葉輪磨損速率下降28.1%，蝸殼磨損速率下降39.95%。說明使用碳化鎢鍍層可以很好地降低離心泵磨損，提高使用壽命。

5 結論

本文使用CFD-DEM耦合計算方法，計算了不同固液兩相流工況對大排量混砂離心泵顆粒運動過程及磨損特性進行了研究。結論如下：

1） 蝸殼雙流道結構會導致外流道顆粒運動滯后，且顆粒進入蝸殼后向外側偏移。

2） 蝸殼主要磨損區域為雙流道分隔板以及增壓管根部。葉輪主要磨損區域發生在葉片根部邊及葉片壓力面中部。

3） 在其他條件相同時，葉輪轉速每上升10 r/min，蝸殼的沖擊磨損量和摩擦磨損量分別平均增加13%和18.5%。葉輪的沖擊磨損量和摩擦磨損量分別平均增加28.5%和8%。

4） 在其他條件相同時，入口流量每增加20%，蝸殼的沖擊磨損量和摩擦磨損量分別增加85%和53%。葉輪的沖擊磨損量和摩擦磨損量分別增加31.5%和38.5%

5） 離心泵運行0.3 s后，蝸殼及葉輪的磨損量基本呈線性增長趨勢。相同條件下離心泵的沖擊磨損速率高于摩擦磨損速率比。蝸殼磨損速率主要受流量影響，葉輪磨損速率主要受轉速影響。同時葉輪的磨損量要比蝸殼大4～5倍。

6） 使用碳化鎢鍍層使葉輪及蝸殼的磨損速率分別降低28.1%和39.95%，可以很好地降低離心泵磨損，提高使用壽命。

參考文獻：

[1] 李文維. 小排量混砂增壓泵車的研制[J]. 科技與創新， 2020，（10）： 123-124.

[2] 袁旭軍，吳漢川. 從我國壓裂市場現狀談大型壓裂機組的研制[J]. 石油天然氣學報，2010， 32（3）： 383-385.

[3] 劉棟，倪子建，黃凱，等. 基于CFD-DEM的離心泵葉輪磨損特性研究和優化設計[J]. 流體機械， 2022， 50（9）： 26-32.

[4] 吳漢川，王峻喬，仇黎明. 混砂車吸入排出性能研究[J]. 石油機械，2013，41（3）： 92-95.

[5] 趙斌娟，王澤. 離心泵葉輪內流數值模擬的現狀和展望[J]. 農機化研究，2002（3）： 49-52.

[6] SHI Yifang，Tang Lingfeng，TAN Yinwu，et al. Optimization of the Structural Parameters of a Plastic Centrifugal Pump[J]. Fluid Dynamics amp;amp;Materials Processing，2022，

18（3）：713-736.

[7] 程效銳，董富弟，楊從新，等. 基于顆粒摩擦和碰撞模型的離心泵葉片磨損預測[J]. 蘭州理工大學學報，2015，41（2）： 55-60.

[8] 廖姣，賴喜德，廖功磊，等. 基于固液兩相流的離心泵內部流場數值分析[J]. 熱能動力工程，2017，32（5）： 95-99，

139-140.

[9] Kafui D k，Johnson S，Thornton C，et al.Parallelization of a Lagrangian-Eulerian DEM/CFD code for application to fluidized beds[J].Powder Technology，2011，207（1/3）： 270-278.

[10] TANG cheng，YANG Youchao，LIU Pengzhan，et al. Prediction of Abrasive and Impact Wear Due to Multi-Shaped Particles in a Centrifugal Pump via CFD-DEMCoupling Method[J]. Energies，2021，14（9）：1-15.

[11] 黃凱，劉棟，尤保健，等. 顆粒濃度對離心泵性能及磨損影響的研究[J]. 流體機械，2022，50（2）： 35-42.

[12] 王田田，支嘉才，楊具瑞，等. 基于計算流體動力學與離散元法的離心泵內流場及磨損的數值模擬[J]. 湖南農業大學學報（自然科學版），2022，48（2）： 235-241.

[13] 王田田，池曉清，楊具瑞，等. 顆粒特性對離心泵葉輪葉片的磨損分析[J]. 水動力學研究與進展A輯，2022，

37（2）： 181-189.

[14] 趙偉國，鄭英杰，劉宜，等. 沙粒體積分數對離心泵磨損特性影響的數值分析[J]. 排灌機械工程學報， 2018，

36（2）： 98-103.

[15] 汪家瓊，蔣萬明，孔繁余，等. 固液兩相流離心泵內部流場數值模擬與磨損特性[J]. 農業機械學報，2013，

44（11）： 53-60.

[16] 李曉俊，袁壽其，潘中永，等. 離心泵邊界層網格的實現及應用評價[J]. 農業工程學報，2012，28（20）： 67-72.

[17] 孫銳，楊釗.高速通道壓裂過程中支撐劑運移規律研究[J]. 河南科學，2023，41（4）：516-523.

（編輯：韓睿超）