基于區域綜合風險評估的城市重點防衛區域選擇

摘 要：針對城市防御力量有限條件下如何選擇高風險重點保衛區域，使有限力量效用最大化、城市風險最小化的問題，提出了一種基于區域綜合風險評估的城市重點防衛區域選擇方法。首先，從入侵方和防御方角度思考，構建合理的保衛目標風險評估指標體系;其次，基于等效能量思想提出了權積歸一法來確定保衛目標風險指標的組合權重，進而計算目標風險值;接著，根據質心理論結合目標距離測度與重要程度構建目標分布加權質心計算模型，并以此為基準，建立離差矩陣計算區域目標分布離散度;最后，依據風險雷達圖面積構造區域綜合風險評估函數，并結合某城市Ⅰ～Ⅵ區目標情況對各區域的綜合風險進行定量評估。結果表明，相比于目標風險耦合方法，該方法能夠更準確地實現區域綜合風險評估，為城市重點防衛區域選擇及有限力量高效部署提供決策依據。

關鍵詞：有限防御力量;區域綜合風險;組合權值;分布離散度

中圖分類號：U298 文獻標志碼：A DOI：10.3969/j.issn.1673-3819.2025.01.008

Selection of key urban defense areas based on regional comprehensive risk assessment

WEI Hua， WANG Xiaoxia， YANG Fengbao， JIA Qi

（School of Information and Communication Engineering， North University of China， Taiyuan 030051， China）

Abstract： Aiming at the problem of how to select high risk key defense area under the condition of limited urban defense force， to maximize the utility of limited force and minimize the urban risk， this paper proposes a method of selecting key defense area based on regional comprehensive risk assessment. Firstly， a reasonable risk assessment index system is constructed from the perspective of the intruder and the defender. Secondly， based on the idea of equivalent energy， the weight product normalization method is proposed to determine the combined weight of the target risk index， and then calculate the target risk value. Then， according to the centroid theory， the weighted centroid calculation model of target distribution is constructed， and the dispersion matrix is established to calculate the dispersion of regional target distribution. Finally， the regional comprehensive risk assessment function is constructed according to the area of risk radar map， and the comprehensive risk of each region is quantitatively assessed according to the target situation of districts I to VI of a city. The results show that compared with the target risk coupling method， the proposed method can realize the regional comprehensive risk assessment more accurately， and provide decision-making basis for the selection of key urban defense areas and the efficient deployment of limited forces.

Key words： limited defense forces; regional comprehensive risk; combinatorial weights; dispersion of distribution

隨著國際形勢的不穩定性加劇，多地沖突頻發。城市作為主要發生地［1］，受到戰略規劃、資源限制和地形阻礙等因素的影響，不同地區間的防御力量調配變得困難，導致防御力量分散且有限。因此，需要對城市各個區域的綜合風險進行精確評估，確定城市重點防衛區域，指導有限力量合理分配，確保力量效用最大化，使城市風險最小化。

目前，學者們的研究主要集中于對特定保衛目標的風險評估。例如，康錦偉［2］研究了城市中重點目標遭受恐怖襲擊的風險，并以地鐵站為例，為應急力量的資源配置提供依據。吳敏［3］構建了機場涉恐風險評估模型，對進一步建立我國機場風險評估機制和方法提供一定的科學依據。彭子眉等［4］基于威脅發生可能性、武器破壞性和目標脆弱性對火車站進行了風險評估，為后續開展反恐防范和應對工作提供了理論支持。孟婷［5］采用K-means聚類分析方法對外交機構遭受襲擊的風險進行定量、客觀的評估，研究成果對外交機構反恐策略具有重要的指導意義。這些研究實現了對特定目標的風險評估，但在城市防御力量不足情況下，重點防衛區域的選擇和有限力量的分配需考慮整體目標群的綜合風險，因此，針對特定保衛目標的風險評估方法并不能有效指導有限力量的分配。

對此，本文提出了一種區域綜合風險評估方法。以保衛目標風險評估為基礎，確定目標風險均值;在此基礎上，從目標距離測度及目標重要程度出發，通過離差矩陣確定區域目標離散度;而后，利用風險雷達圖面積原理將目標風險均值、目標離散度及目標數量因素結合，全面評估區域綜合風險。

1 保衛目標風險評估

1．1 保衛目標風險評估體系構建

保衛目標風險評估指標體系構建是區域綜合風險評估過程的基礎。綜合考慮入侵方威脅程度與保衛目標安全程度，確定了入侵方選擇目標意圖I1、相對破壞能力I2、相對干擾能力I3、己方目標重要程度I4、目標易損程度I5與目標隱蔽程度I6等6個風險評估指標及其影響因素，具體如圖1所示。

（1）指標合理性檢驗

結合城市防空的特點，為評估保衛目標風險，設計了包含6個指標條目的調查量表，并利用Cronbach's α系數和Pearson相關系數度量其一致性與相關性［6］。當Cronbach's α系數值大于0．7時，可認為條目之間的內在一致性較好;當Pearson相關系數值大于0．4或小于-0．4時，說明指標條目與目標風險間相關性較強。結果如表1所示。

通過計算量表的Cronbach's α系數值為0．852，大于0．7，且如表1所示，刪除各項后的Cronbach's α系數值均小于0．852。各指標條目的Pearson相關系數值皆處于-1，-0．4）∪（0．4，1范圍內。由此說明評估指標選取較為合理，能有效反映目標風險。

（2）指標函數構建

1．2 保衛目標風險評估指標權重確定

合理確定指標權重是確保風險評估有效性的關鍵步驟。為了消除傳統算術平均組合賦權法對極端值的敏感與乘法合成組合賦權法的倍增效應［13］，本文根據物理學中求兩個不同能量源同時作用的等效能量思想，提出了采用幾何平均計算方法的權積歸一法進行主、客觀權重融合，獲得更為合理的指標組合權重。權積歸一法具體步驟如下：

權積歸一法的原理是在乘法集成的基礎上進行開方處理，且開方數由組合的權重種類數來確定。其中，乘法集成的運用消除了極端值的影響;而開方處理消除了乘積的倍增效應。因此，權積歸一法能夠更為合理地確定指標組合權重。

1．3 保衛目標風險值計算

2 區域綜合風險評估模型構建

在區域綜合風險評估中，通過目標風險均值Fs、目標離散度σ及目標數量N構建區域綜合風險模型，如圖2所示。

2．1 區域目標分布離散度計算

在防御力量有限條件下，當城市區域內重要目標呈現較高程度的聚集時，可通過在關鍵區域集中部署防御力量，以較少部署點達到有效覆蓋，目標防御被突破的風險相對較小;相反，若目標分布較為分散，分散的防御措施會導致每個防御區域的力量相對薄弱，被突破的風險也會增加。因此，目標分布的離散度σ可作為評估區域綜合風險的關鍵指標。然而，由于每個目標的重要程度不同，需要引入質心理論［15］計算目標分布加權質心值Cd，進而構建離差矩陣D。

2．2 區域綜合風險函數構造

首先，計算目標風險均值Fs，再對目標風險均值Fs、目標分布離散度σ及目標數量N指標進行標準化處理，得到處理后的指標Fs′、N′、σ′。然后，根據風險雷達圖面積原理，利用處理后的指標構造區域綜合風險函數F0。

風險雷達圖的面積原理，如圖3所示。指標N′、F′s、σ′呈正三角形排列，而每個區域指標值點的連線能夠形成面積不同的三角形ΔS1、ΔS2、ΔS3。三角形的面積大小取決于指標值點離坐標原點的距離，即指標值的大小。指標值越大則三角形面積越大。同時，指標值的增大也意味著風險值的提升。因此，可通過三角形面積大小表示各區域綜合風險的相對大小。

3 實驗驗證及分析

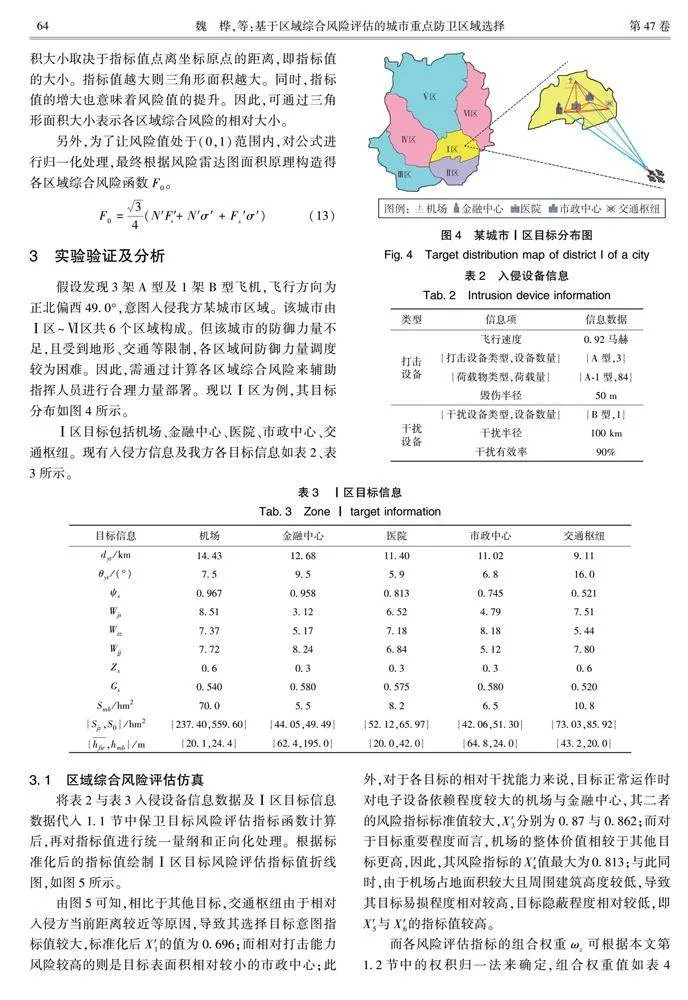
假設發現3架A型及1架B型飛機，飛行方向為正北偏西49．0°，意圖入侵我方某城市區域。該城市由Ⅰ區～Ⅵ區共6個區域構成。但該城市的防御力量不足，且受到地形、交通等限制，各區域間防御力量調度較為困難。因此，需通過計算各區域綜合風險來輔助指揮人員進行合理力量部署。現以Ⅰ區為例，其目標分布如圖4所示。

Ⅰ區目標包括機場、金融中心、醫院、市政中心、交通樞紐。現有入侵方信息及我方各目標信息如表2、表3所示。

3．1 區域綜合風險評估仿真

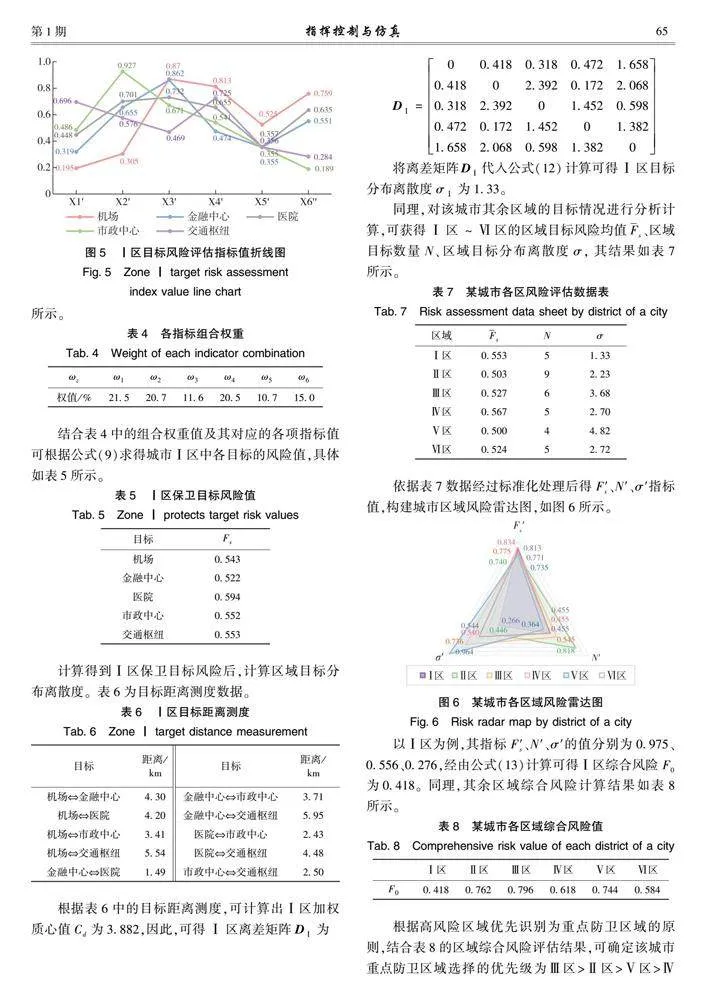
將表2與表3入侵設備信息數據及Ⅰ區目標信息數據代入1．1節中保衛目標風險評估指標函數計算后，再對指標值進行統一量綱和正向化處理。根據標準化后的指標值繪制Ⅰ區目標風險評估指標值折線圖，如圖5所示。

由圖5可知，相比于其他目標，交通樞紐由于相對入侵方當前距離較近等原因，導致其選擇目標意圖指標值較大，標準化后X′1的值為0．696;而相對打擊能力風險較高的則是目標表面積相對較小的市政中心;此外，對于各目標的相對干擾能力來說，目標正常運作時對電子設備依賴程度較大的機場與金融中心，其二者的風險指標標準值較大，X′3分別為0．87與0．862;而對于目標重要程度而言，機場的整體價值相較于其他目標更高，因此，其風險指標的X′4值最大為0．813;與此同時，由于機場占地面積較大且周圍建筑高度較低，導致其目標易損程度相對較高，目標隱蔽程度相對較低，即X′5與X′6的指標值較高。

而各風險評估指標的組合權重ωz可根據本文第1．2節中的權積歸一法來確定，組合權重值如表4所示。

結合表4中的組合權重值及其對應的各項指標值可根據公式（9）求得城市Ⅰ區中各目標的風險值，具體如表5所示。

計算得到Ⅰ區保衛目標風險后，計算區域目標分布離散度。表6為目標距離測度數據。

同理，對該城市其余區域的目標情況進行分析計算，可獲得Ⅰ區～Ⅵ區的區域目標風險均值s、區域目標數量N、區域目標分布離散度σ，其結果如表7所示。

依據表7數據經過標準化處理后得F′s、N′、σ′指標值，構建城市區域風險雷達圖，如圖6所示。

以Ⅰ區為例，其指標F′s、N′、σ′的值分別為0．975、0．556、0．276，經由公式（13）計算可得Ⅰ區綜合風險F0為0．418。同理，其余區域綜合風險計算結果如表8所示。

根據高風險區域優先識別為重點防衛區域的原則，結合表8的區域綜合風險評估結果，可確定該城市重點防衛區域選擇的優先級為Ⅲ區gt;Ⅱ區gt;Ⅴ區gt;Ⅳ區gt;Ⅵ區gt;Ⅰ區。

3．2 結果分析

3．2．1 區域綜合風險評估結果分析

由3．1節評估結果可以得出該城市各區域風險程度情況如圖7所示。

結合圖7與表7、表8內容可以看出，Ⅲ區目標分布較為分散且目標數量較多，因此，綜合多方面因素評估后得到的風險值最大，區域重點防衛選擇的優先次序最高;而Ⅱ區的目標數量與Ⅴ區的目標分布離散度遠大于其他區域，因此，在力量有限條件下綜合風險和優先次序也相對較高;同時，對于目標數量相同且分布離散度相近的Ⅵ區與Ⅳ區來說，Ⅳ區的目標風險均值為0．567，大于Ⅵ區，因此，Ⅳ區被選擇重點防衛的優先次序大于Ⅵ區;此外，在這些區域中，Ⅰ區的分布離散度最小為1．33，綜合其他因素考慮后的區域綜合風險值最小，因此，Ⅰ區的選擇次序排在最末。根據以上結果分析表明，本文所采用的基于區域綜合風險評估的城市重點防衛區域選擇方法較為合理且可行。

3．2．2 權積歸一法與其他組合賦權法對比分析

3．2．3 風險耦合方法與本文方法結果對比分析

為了驗證本文方法的合理性，采用風險耦合方法［18-19］將現有的保衛目標風險進行耦合，所得區域耦合風險FRCT作為區域綜合風險F0的對照數據，結果如表11所示。

由表11可知，采用風險耦合法獲得的該城市重點防衛區域選擇的優先排序為Ⅲ區gt;Ⅱ區gt;Ⅳ區gt;Ⅵ區gt;Ⅴ區gt;Ⅰ區，與本文方法得到的排序結果近似，由此可說明本文方法較為合理。其中，與風險耦合法不同的是采用本文方法計算時，考慮了力量不足情況下評估區域綜合風險需重視的目標整體位置分布因素。因此，在本文排序結果中目標分布離散度最大的Ⅴ區綜合風險大于Ⅵ區和Ⅳ區，即Ⅴ區被優先選擇的次序更高。另外，通過計算表11兩組數據的方差可得，FRCT組方差為0．0007，數據區分度較低;F0組方差為0．0172，數據差異化較為顯著，更利于劃分城市區域優先防衛次序，對輔助指揮人員在防御力量有限條件下城市力量的合理部署更具有優越性。

4 結束語

本文根據雷達圖面積原理，利用目標風險均值、目標離散度、目標數量構造了區域綜合風險評估函數并結合實際數據對某城市區域綜合風險進行評估，確定了在防御力量有限條件下城市重點區域的選擇優先級。其中，在確定目標風險均值時，根據風險影響因素構建了保衛目標風險評估指標體系，確定了指標函數，并且為了提高指標權重的合理性，提出了一種不受極端值和乘積倍增效應影響的組合權重計算方法，并通過實驗數據進行了驗證。另外，在計算目標離散度時，考慮目標自身重要性對風險值的影響，引入了質心理論思想，將距離測度結合目標重要程度計算出的加權質心值作為基準，構建了離差矩陣，保證了離散度數據的合理性。通過實驗驗證，本文方法對區域綜合風險的評估具有一定可行性，能夠為指揮人員在有限力量條件下，確定重點防衛區域，合理分配防御力量提供重要依據，進而有效降低城市風險。后續，作者也將在區域綜合風險模型構建上進行深入研究，探索保衛目標風險間更內在的聯系，提升區域綜合風險評估的數據深度。

參考文獻：

[1] 馮玉軍. 俄烏沖突下東亞安全格局新趨勢［J］. 東北亞學刊， 2023（2）： 21-33， 146.FENG Y J. The new trend of East Asian security pattern in the context of Russia-Ukraine conflict［J］. Journal of Northeast Asia Studies， 2023（2）： 21-33， 146.

[2] 康錦偉. 城市重點目標恐怖襲擊風險分析方法研究［D］. 北京： 中國人民公安大學， 2021.KANG J W. Study on risk analysis method of terrorist attacks on urban key targets［D］. Beijing： Chinese People's Public Security University， 2021.

[3] 吳敏. 基于仿真模擬的公共交通樞紐風險評估研究——以N機場為例［D］. 北京： 中國人民公安大學， 2020.WU M. Research on terrorist attack risk assessment of public transportation hub based on simulation ［D］. Beijing： Chinese People's Public Security University， 2020.

[4] 彭子眉， 金華. 基于攻防對抗的反恐重點目標風險評估模型研究［J］. 中國人民公安大學學報（自然科學版）， 2022， 28（3）： 43-50.PENG Z M， JIN H. Research on risk assessment model for key targets of anti-terrorism based on attack-defense confrontation［J］. Journal of People's Public Security University of China（Science and Technology）， 2022， 28（3）： 43-50.

[5] 孟婷. 基于K-means算法的外交機構恐怖主義風險評估［J］. 情報探索， 2021（1）： 47-55.MENG T. Terrorism risk assessment of diplomatic agencies based on K-means clustering analysis［J］. Information Research， 2021（1）： 47-55.

[6] 牛軍鋒， 甘旭升， 劉影， 等. 空中目標威脅的ABC-RVM評估方法［J］. 火力與指揮控制， 2022， 47（4）： 63-68， 74.NIU J F， GAN X S， LIU Y， et al. ABC-RVM assessment method for air target threat［J］. Fire Control ＆ Command Control， 2022， 47（4）： 63-68， 74.

[7] 汪鑫， 龍光正， 汪志宏， 等. 基于灰色聚類和序關系的防空保衛目標排序研究［J］. 彈箭與制導學報， 2018， 38（2）： 25-29.WANG X， LONG G Z， WANG Z H， et al. Based on the grey clustering method to resolve the defend target comprehensive sequencing in the mufti-stage air defense combat［J］. Journal of Projectiles， Rockets， Missiles and Guidance， 2018， 38（2）： 25-29.

[8] 賈琦， 吉琳娜， 王肖霞， 等. 不確定條件下作戰籌劃態勢研判風險預測方法［J］. 指揮控制與仿真， 2024， 46（2）： 141-149.JIA Q， JI L N， WANG X X， et al. Risk prediction method for operational planning situation analysis under uncertain conditions［J］. Command Control ＆ Simulation， 2024， 46（2）： 141-149.

[9] 黃威龍， 何濤. 空中目標威脅度分析與評估方法［J］. 指揮控制與仿真， 2023， 45（5）： 123-128.HUANG W L， HE T. Threat analysis and evaluation method of aerial targets［J］. Command Control ＆ Simulation， 2023， 45（5）： 123-128.

[10]馮卉， 張春梅. 基于Vague集的防空重點保衛目標優選與排序［J］. 管理科學與工程， 2019， 8（2）：132-136.FENG H， ZHANG C M. Selecting and sequencing of the important defending targets in defense zone based on vague sets［J］. Management Science and Engineering， 2019， 8（2）：132-136.

[11]馮卉， 毛紅保， 邢清華. MADM組合賦權的防空重點保衛目標優選與排序［J］. 火力與指揮控制， 2014， 39（8）： 5-8.FENG H， MAO H B， XING Q H. Selecting and sequencing of important defending targets in defense zone based on combination weighting for MADM［J］. Fire Control ＆ Command Control， 2014， 39（8）： 5-8.

[12]孫東振， 史瑞芝， 張振華， 等. 切尾統計算法的優化及應用［J］. 中國印刷與包裝研究， 2010， 2（2）： 29-32.SUN D Z， SHI R Z， ZHANG Z H， et al. Application and optimization of trimmed statistical algorithm［J］. China Printing and Packaging Study， 2010， 2（2）： 29-32.

[13]MU X P， WANG Y T， LIU H X， et al. Flood risk assessment of Hun-Tai Area due to dike break based on HEC-RAS［J］. Journal of Water Resources Research， 2020， 9（3）： 289-300.

[14]黃明田， 李澤玲. 基于直覺模糊層次分析法的90后知識型員工績效評價與激勵策略研究［J］. 數學的實踐與認識， 2019， 49（23）： 230-239.HUANG M T， LI Z L. Study on performance appraisal and incentive strategy of 90s knowledge worker based on intuitionistic fuzzy hierarchy model［J］. Mathematics in Practice and Theory， 2019， 49（23）： 230-239.

[15]NI J H， CHEN J， WU Y L， et al. Method to determine the centroid of non-homogeneous polygons based on suspension theory［J］. ISPRS International Journal of Geo-Information， 2022， 11（4）： 233.

[16]魏久傳， 許玉陽， 謝道雷， 等. 基于距離函數組合賦權法的突水危險性評價［J］. 中國礦業， 2021， 30（4）： 162-167.WEI J C， XU Y Y， XIE D L， et al. The risk assessment of water bursting based on combination rule of distance function［J］. China Mining Magazine， 2021， 30（4）： 162-167.

[17]鄒國良， 劉娜娜. 基于組合賦權-云模型的離子型稀土礦開采工藝評價［J］. 有色金屬科學與工程， 2021， 12（4）： 88-95.ZOU G L， LIU N N. Evaluation on the mining technology of ion-adsorption rare earth ore based on combined weighting-cloud model［J］. Nonferrous Metals Science and Engineering， 2021， 12（4）： 88-95.

[18]王乾坤， 亢顯衛， 朱科. 地鐵深基坑施工風險耦合評價方法［J］. 東北大學學報（自然科學版）， 2021， 42（8）： 1 152-1 158.WANG Q K， KANG X W， ZHU K. Coupling evaluation method of the construction risk for subway deep foundation pit［J］. Journal of Northeastern University（Natural Science）， 2021， 42（8）： 1 152-1 158.

[19]李勝男， 閆海峰， 吳鵬飛， 等. 基于N-K模型的鐵路運營事故風險耦合性分析［J］. 現代城市軌道交通， 2023（11）： 103-109.LI S N， YAN H F， WU P F， et al. A risk coupling analysis of railway operation accident based on the N-K model［J］. Modern Urban Transit， 2023（11）： 103-109.

（責任編輯：張培培）