基于蒙特卡羅法的雷達網覆蓋面積計算及仿真

摘 要：雷達網覆蓋區域的大小是衡量防空體系性能的重要指標之一，對優化雷達組網布局設計，最大限度發揮雷達網的綜合效益具有重要意義。由于雷達網的探測概率是各個雷達共同作用的結果，其覆蓋區域圖形非常復雜，難以利用常規方法求出解析解。通過分析多部雷達對目標的聯合概率與雷達參數、目標距離之間的相互關系，建立了判定約束條件，采用蒙特卡羅法，將面積計算問題轉化成為計算平面內隨機坐標點滿足約束條件的點數問題，并給出了具體算法的過程。與同類算法比較而言，該算法的結構清晰簡單，易于擴展。仿真實驗結果表明了算法的可行性。

關鍵詞：雷達組網;覆蓋面積;蒙特卡羅法;聯合概率

中圖分類號：TN957 文獻標志碼：A DOI：10.3969/j.issn.1673-3819.2025.01.017

A method for calculating the coverage area of radar network

based on Monte Carlo method and its simulation

WANG Yinlong， WANG Dan， MA Juntao， ZHAO Deyong

（Shijiazhuang Campus of the Army Engineering University， Shijiazhuang 050003，China）

Abstract：The size of the radar network coverage area is one of the important indicators to measure the performance of the air defense system， and it is of great significance to optimize the layout design of radar network and to maximize the comprehensive uniform chamber benefit of radar network. Since the probability of detecting a target by the radar network is the result of the joint action of various radars， the graph of its coverage area is very complex and difficult to obtain an analytical solution by conventional methods. By analyzing the relationship between the joint probability of multiple radars detecting a target and the radar parameters and target distance， the constraints are determined， and the basic idea of Monte Carlo method is used to transform the area calculation problem into a problem of calculating the number of points satisfying the constraints in a plane. The process of the specific algorithm is given. Compared with similar algorithms， the structure of this algorithm is clear and simple， and it is easy to extend. Through simulation experiments， the feasibility of the algorithm is verified.

Key words：radar networking; coverage area; Monte Carlo method; joint probability

雷達組網是將多部不同體制、頻段和極化方式的雷達進行組網部署，實現多部雷達間的戰術協同，從而構成全方位、立體化、多層次的防空警戒體系。在防空效能評估中，探測區域覆蓋面積是一項重要的性能指標，是衡量雷達網探測性能優劣的關鍵依據［1-3］。由于雷達網覆蓋區域是多部雷達共同作用的結果，其形狀往往是由雷達的性能參數、相互位置、地域環境等多個因素共同作用形成的復雜圖形。其投影面積的大小與雷達網中單部雷達的覆蓋面積相關，但并不是把各部雷達覆蓋面積直接相加或是簡單取“并集”。

理論和實踐表明，如果雷達位置布局適當，那么雷達網的探測區域面積將會大于各個雷達探測面積的加和。然而事實上，雷達網覆蓋區域的邊界難以用一個曲線方程準確表示出來，其面積也很難求出解析解。

近年來，針對上述問題，許多學者進行了探索研究，韓雙連等［4］利用單部雷達在指定高度層上的探測包絡數據，并利用Qt軟件實現對各包絡數據的圖形計算，再通過多邊形面積計算及坐標轉換投影實現了雷達網覆蓋面積的計算;程曉光等［5］提出了考慮地形遮蔽和目標散射截面的計算單部雷達探測范圍的方法，并在此基礎上利用積分思路計算高程圈面積，從而給出了雷達網在不同高程上的探測區域面積計算方法;丁宇等［6］通過判斷雷達網內各雷達之間的相互覆蓋情況，并計算相互覆蓋雷達之間的交點，并根據交點將各雷達區域邊進行界劃分，從而提出了分弧段角度法計算重疊覆蓋區域的算法。但是，這些方法基本都是在沒有考慮多部雷達聯合探測概率大于單個雷達探測概率的情況進行的計算。因此，有必要從概率的角度出發進一步研究雷達組網的覆蓋面積問題。

1 雷達網的探測范圍

1．1 雷達探測距離

雷達最大作用距離與雷達各分機參數以及目標參數有關。考慮電磁波傳播環境以及地球曲率的影響，雷達直視距離由雷達天線架設高度和目標高度決定。而對于單部遠程預警雷達而言，其最大作用距離要小于雷達直視距離，此時雷達探測距離即為雷達最大作用距離。換句話說，單部遠程預警雷達的探測距離受地球曲率影響不大。而對于雷達組網，其探測范圍是各部雷達的探測距離共同作用的結果。

1．2 單部雷達的探測概率

通常情況，對于某部雷達而言，不能直接地計算它的探測距離是多遠，而是在給定目標被探測到的概率大于或等于某個特定閾值時雷達的探測距離。根據文獻［7］可知單部雷達的探測概率與距離之間的關系為

1．3 多部雷達的聯合探測概率

1．4 雷達網的探測覆蓋面積

由此可知，空間中的所有滿足公式（9）的點所構成的區域就是雷達網的空間警戒區域。由公式（9）可知，在某一高度層上，探測區域的圖形非常復雜，無法通過積分的方法求解出它的面積。然而，可以借鑒蒙特卡羅法的基本思想，將計算面積問題轉化成為計算平面內隨機坐標點滿足約束條件的點數問題。

2 雷達網覆蓋面積計算

2．1 蒙特卡羅法的特點

蒙特卡羅法的思想誕生于18世紀法國著名專家Buffon進行的投針實驗，即通過投針實驗得到圓周率π的數值［8］。蒙特卡羅法也稱為隨機抽樣法或者統計實驗法，即通過產生隨機數進行統計實驗，利用計算得到的平均值或者概率等具有統計特征的值來表示問題的數值解［9-10］。相比于與其他方法，蒙特卡羅方法具有很多優點，如：適應性強，受具體問題約束限制小;算法結構簡單清晰，適合在普通計算機上變成實現;收斂速度與問題維數無關等。雖然蒙特卡羅法往往存在一定的精確性問題，但鑒于雷達探測目標本身屬于概率問題，蒙特卡羅法仍舊非常適合雷達網覆蓋區域問題。

2．2 算法的主要過程

2．3 算法的時間復雜度

通過分析整個算法的循環次數，發現其主要與雷達的數量、高度層數以及隨機生成的點數相關。當雷達網給定后，雷達數量將不再變化，且數量通常不會很大（不超過2位數），基本可以忽略其影響。于是，高度層數H和隨機生成點數M將是影響程序運行時間的主要因素。因此，當算法計算整個空間的三維覆蓋區域時，其時間復雜度為O（n2）;當算法計算某一高度層的覆蓋區域面積時，其時間復雜度為O（n）。

可以看出，算法計算的理論精度與算法的時間復雜度之間是相互矛盾的。因此，在編程實踐中，可根據具體需要，合理確定高度層數和隨機點的個數，以此來平衡精度與速度之間的矛盾。

3 仿真實驗

為了驗證算法的可行性，對不同布站方式的雷達網進行了仿真［11-12］。實驗表明，該算法可以實現多部雷達組網情況下復雜覆蓋區域的計算，且運算時間和精度可根據需要進行調整控制。

3．1 相關參數

3．2 實驗結果

利用上述實驗環境和初始化的參數進行仿真實驗。表1所示數據為垂直高度為0時的部分計算結果。通過對比分析發現，3部雷達組成的雷達網按等邊三角形布置時，起初其覆蓋面積隨間隔增大而增大。當各雷達彼此間隔為80 km時覆蓋面積達到最大，此后隨距離增大而減小，并趨于收斂，這一穩定值即為每部雷達單獨工作時覆蓋面積之和。這是因為，當雷達間隔達到一定距離后，彼此因聯合而產生的作用越來越低。

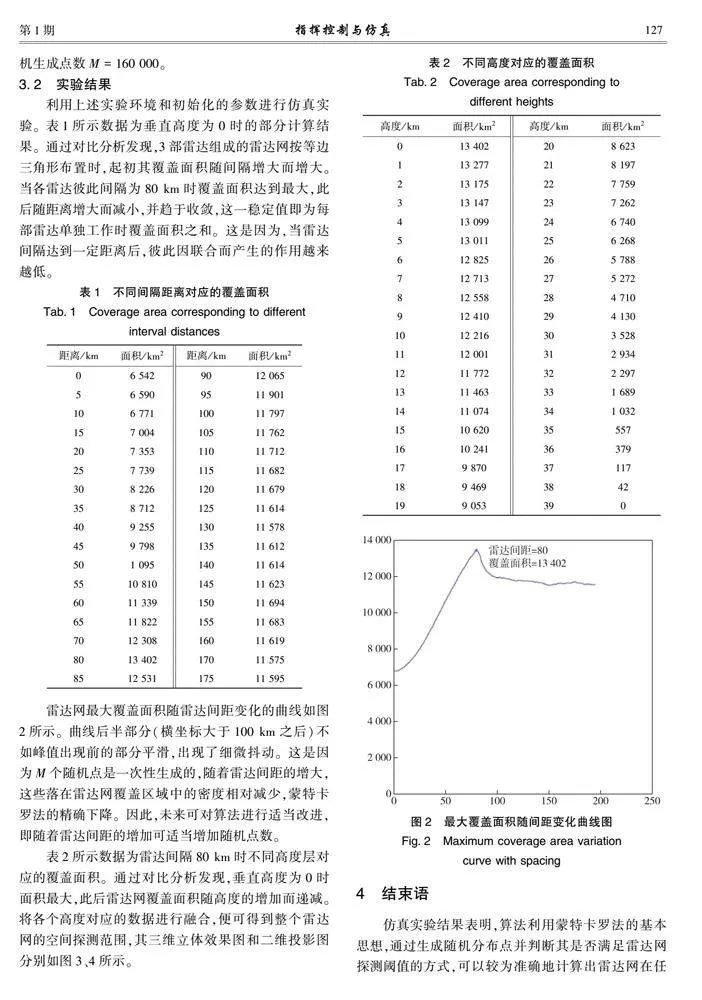
雷達網最大覆蓋面積隨雷達間距變化的曲線如圖2所示。曲線后半部分（橫坐標大于100 km之后）不如峰值出現前的部分平滑，出現了細微抖動。這是因為M個隨機點是一次性生成的，隨著雷達間距的增大，這些落在雷達網覆蓋區域中的密度相對減少，蒙特卡羅法的精確下降。因此，未來可對算法進行適當改進，即隨著雷達間距的增加可適當增加隨機點數。

表2所示數據為雷達間隔80 km時不同高度層對應的覆蓋面積。通過對比分析發現，垂直高度為0時面積最大，此后雷達網覆蓋面積隨高度的增加而遞減。將各個高度對應的數據進行融合，便可得到整個雷達網的空間探測范圍，其三維立體效果圖和二維投影圖分別如圖3、4所示。

4 結束語

仿真實驗結果表明，算法利用蒙特卡羅法的基本思想，通過生成隨機分布點并判斷其是否滿足雷達網探測閾值的方式，可以較為準確地計算出雷達網在任意高度上的覆蓋范圍。由于本文算法的結構簡單清晰，可以比較容易地與其他優化算法融合，如：可以結合近代優化算法求雷達網的最優布局等。此外，由于雷達網是一個綜合的系統，雷達網的覆蓋面還可能受到天氣、地形以及電磁干擾等因素的影響，下一步可在當前算法基礎上疊加相應的約束條件進一步研究。

參考文獻：

[1] 邵錫軍， 周琳. 預警探測系統雷達組網技術研究［J］. 現代雷達， 2003， 25（9）： 1-4.SHAO X J， ZHOU L. Radar netting technique in early warning detection system［J］. Modern Radar， 2003， 25（9）： 1-4.

［2］ 朱興樂. 雷達組網系統效能評估指標體系設計［J］. 艦船電子對抗， 2019， 42（5）： 48-51， 91.ZHU X L. Design of efficiency evaluation index system of radar networking system［J］. Shipboard Electronic Countermeasure， 2019， 42（5）： 48-51， 91.

［3］ 陳永光， 李修和， 沈陽. 組網雷達作戰能力分析與評估［M］. 北京： 國防工業出版社， 2006.CHEN Y G， LI X H， SHEN Y. "Analysis and evaluation of operational capability of networked radar［M］. Beijing： National Defense Industry Press， 2006.

［4］ 韓雙連， 鐘巍， 施巖龍. 一種雷達網覆蓋面積計算方法及應用［J］. 現代雷達， 2017， 39（12）： 12-14， 19.HAN S L， ZHONG W， SHI Y L. Coverage area compute method for radar net and application［J］. Modern Radar， 2017， 39（12）： 12-14， 19.

［5］ 程曉光，李威，王政偉. 雷達網探測能力計算方法［J］.指揮信息系統與技術，2019，10（4）：77-81.CHENG X G， LI W， WANG Z W. Calculation method for radar network detection capability［J］. Command Information Systems and Technology， 2019， 10（4）：77-81.

［6］ 丁宇， 冉華明. 基于分弧段角度法的雷達網重疊覆蓋區域研究［J］. 計算機仿真， 2020， 37（2）： 4-8， 46.DING Y， RAN H M. Study on the characteristics of overlapping coverage area in radar network based on sub-arc angle method［J］. Computer Simulation， 2020， 37（2）： 4-8， 46.

［7］ 高尚. 兩部雷達最佳部署問題研究［J］. 數學的實踐與認識， 1999， 29（3）： 52-55.GAO S. Research on optimal deploy problem of two sets of radar［J］. Journal of Mathematics in Practice and Theory， 1999， 29（3）： 52-55.

［8］ 謝國瑞. 概率論與數理統計［M］. 北京： 高等教育出版社， 2002.XIE G R. Probability theory and mathematical statistics［M］. Beijing： Higher Education Press， 2002.

［9］ 吳海霞， 劉潞鋒. 蒙特卡羅方法在實際問題中的應用［J］. 太原師范學院學報（自然科學版）， 2009， 8（1）： 76-79.WU H X， LIU L F. Monte Carlo method and applications in solving special problems［J］. Journal of Taiyuan Normal University（Natural Science Edition）， 2009， 8（1）： 76-79.

［10］Sambridge M， Mosegaard K. Monte Carlo methods in geophysical inverse problems［J］. Reviews of Geophysics， 2002，40（3）：1-29.

［11］薛山. MATLAB基礎教程［M］. 3版. 北京： 清華大學出版社， 2017.XUE S. Basic course of MATLAB［M］. 3rd ed. Beijing： Tsinghua University Press， 2017.

［12］（美）Philip J.Schneider， （美）David H.Eberly. "計算機圖形學幾何工具算法詳解［M］. 周長發，譯. 北京： 電子工業出版社， 2005.Schneider P J， Eberly D H. Geometric tools for computer graphics［M］. Beijing： Publishing House of Electronics Industry， 2005.

（責任編輯：李楠）