直線的舞蹈

我們已經(jīng)知道一次函數(shù)的圖象是一條直線。那么，一次函數(shù)y=kx+b（k、b為常數(shù)，且k≠0）的圖象與k、b之間存在什么關(guān)系呢？今天，讓我們在數(shù)學軟件GeoGebra（簡稱GGB）的舞臺上，探索一次函數(shù)的圖象性質(zhì)，一起欣賞“直線的舞蹈”。

k的“變奏”

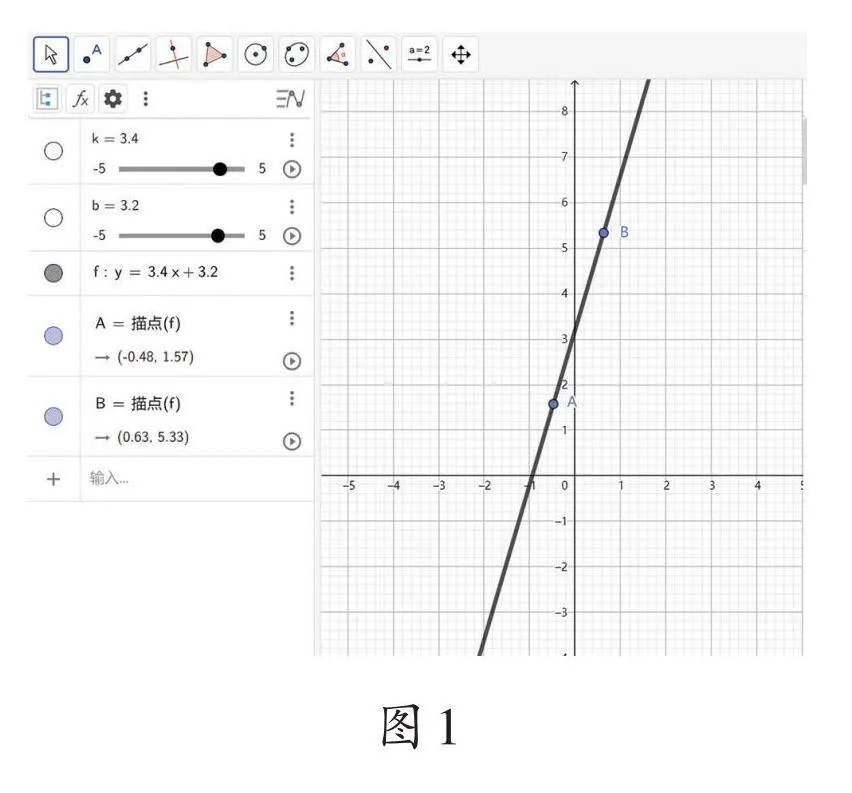
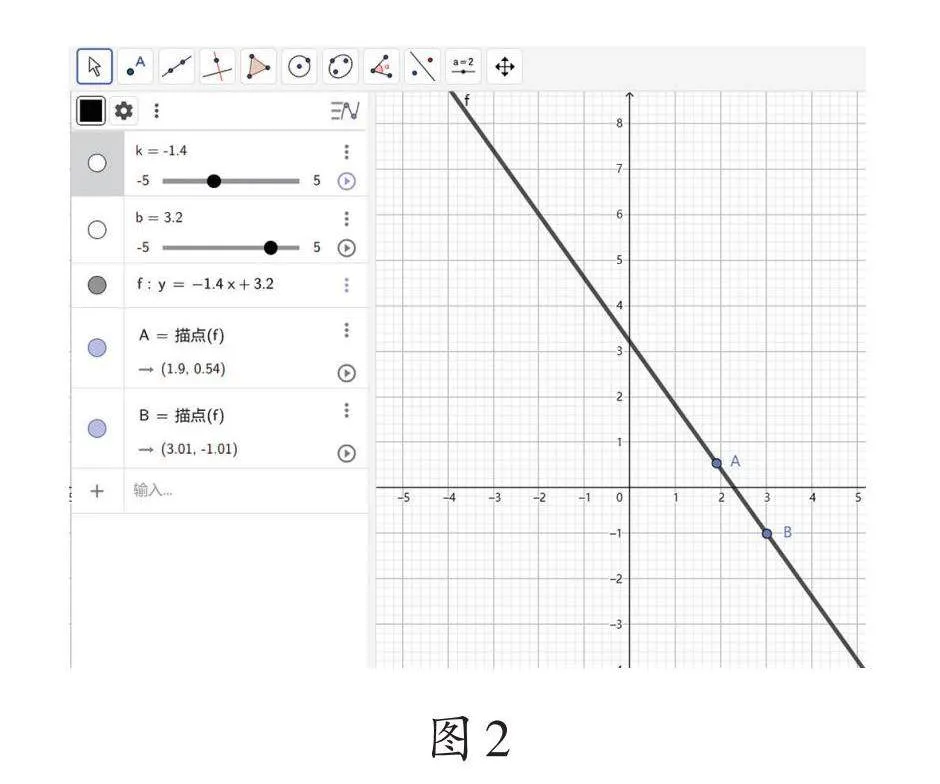
打開軟件，在輸入欄輸入“y=kx+b”，我們會得到一條直線。固定b的值，緩緩拖動k值的滑動條，如圖1、圖2，我們就能見證直線如何隨k值的變化而變化。

我們會發(fā)現(xiàn)，當b值固定時，k的正負決定了直線的傾斜方向：當kgt;0時，直線從左到右呈上升趨勢，y隨x的增大而增大；當klt;0時，直線從左到右呈下降趨勢，y隨x的增大而減小。[k]越大，直線越逼近y軸；[k]越小，直線越逼近x軸。k的值就像是音樂節(jié)拍，直線y=kx+b隨著它的變化翩翩起舞。

b的“游走”

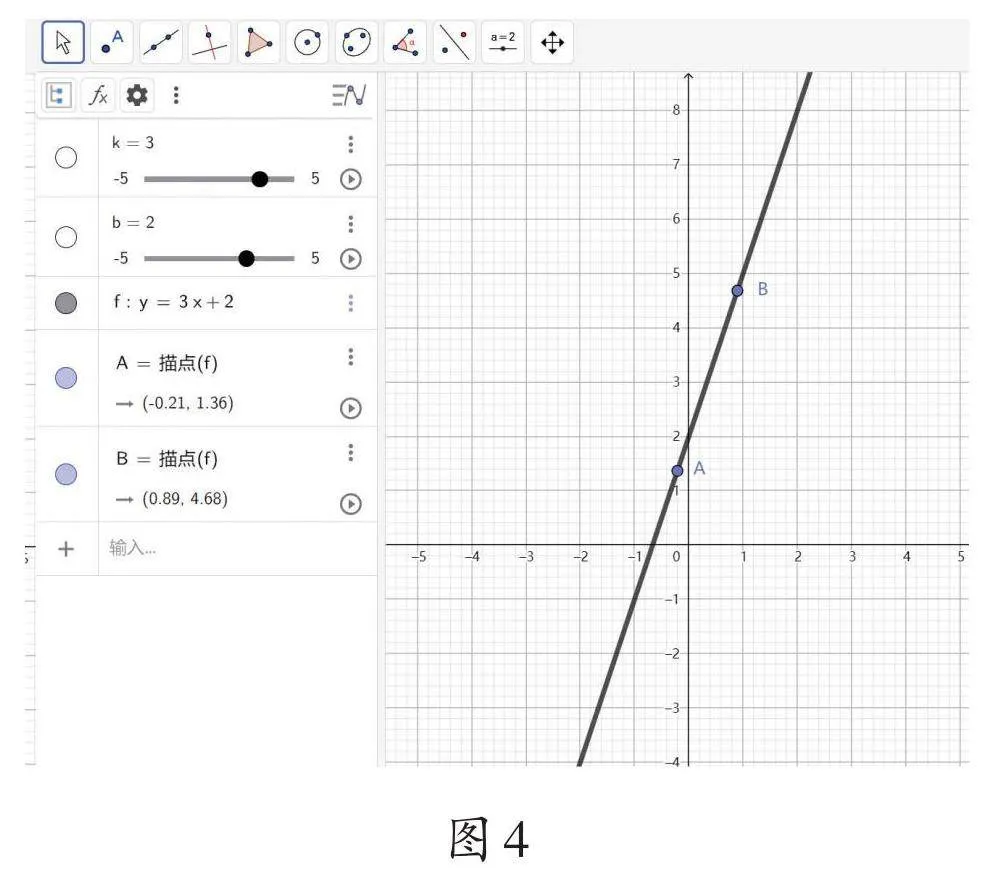
讓我們再固定k的值，緩緩拖動b值的滑動條，一起見證直線如何隨著b值的變化而變化，如圖3、圖4。

我們知道，在一次函數(shù)y=kx+b（k、b為常數(shù)，且k≠0）中，b的值決定了直線與y軸交點的位置。當我們固定k值時，緩緩拖動b值的滑動條，可以看到直線隨著b值的變化上下平移。是視覺差異嗎？讓我們來驗證一下吧！

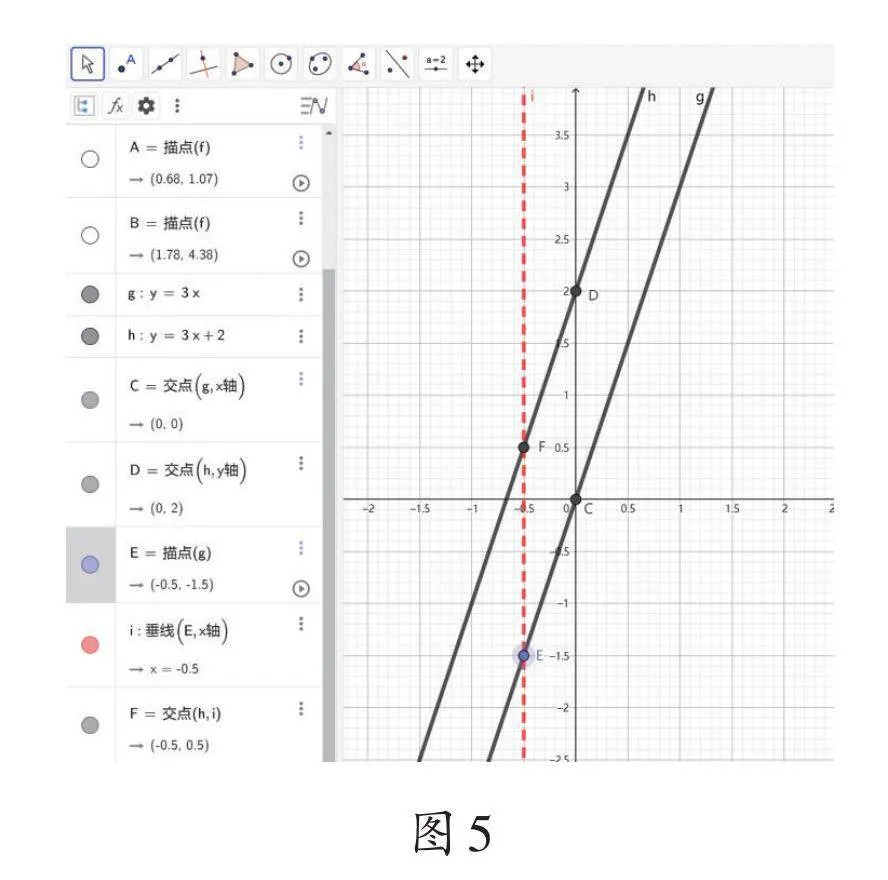
對于直線y=kx+b1，y=kx+b2（k≠0，b1≠b2），我們知道當x值一定時，一次函數(shù)y=kx+b2的值比一次函數(shù)y=kx+b1的值大b2-b1，如圖5。因此兩條直線是平行的。

看來，對于直線y=k1x+b1與直線y=k2x+b2，當k1、b1、k2、b2不同時，直線相交、重合或平行等狀態(tài)是不同的。我們不僅可以用嚴謹?shù)臄?shù)學方法來證明，還可以通過操作GGB進行驗證，讓靜態(tài)的函數(shù)動起來。

在這一系列的動態(tài)變換中，我們能更深刻地理解一次函數(shù)的圖象性質(zhì)。科技的進步，使得我們擁有了更多途徑去學習數(shù)學，理解數(shù)學。……