確定藏寶地

數學來源于生活，又回歸生活。數學家笛卡爾受蜘蛛網的啟發，發明了直角坐標系，從而開啟了將代數與幾何緊密相連的時代。我們在學習平面直角坐標系時，開展了一次數學活動，利用它來解決實際問題——確定藏寶地。

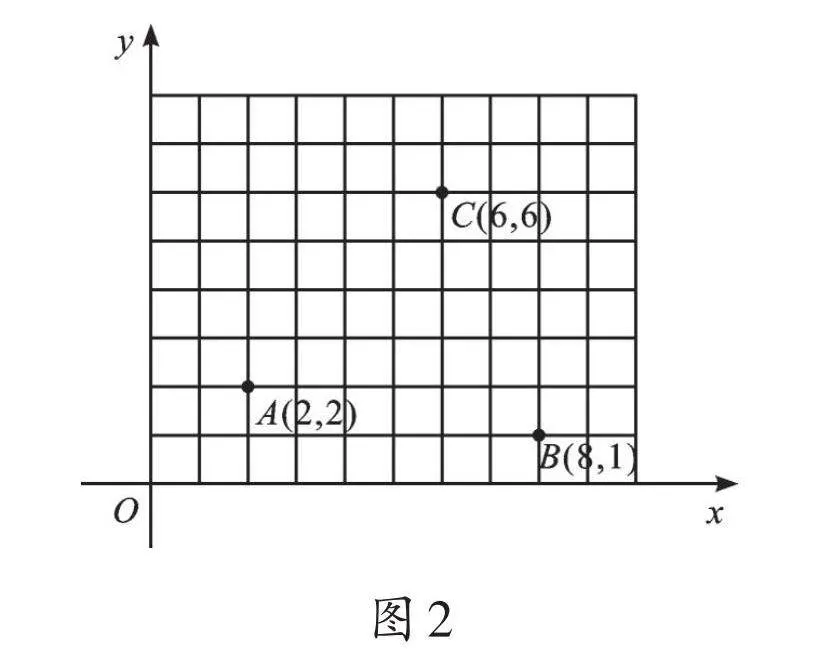
[確定藏寶地][小明在一本課外讀物中看到這樣一段文字和一幅圖：][ 圖1是尋寶者得到的一幅藏寶圖，荒涼的海島上沒有藏匿寶藏的任何標志，只有A、B兩塊天然巨石。

尋寶者從其他資料上查到，島上A、B兩塊巨石在平面直角坐標系中的坐標分別是A（2，2）和B（8，1），藏寶地的坐標是（6，6）。

你能在上面的圖中畫出藏寶地嗎？

根據題目的已知信息和問題要求，不難形成思路：根據A、B兩點的位置確定原點的位置，建立平面直角坐標系，確定寶藏的藏匿位置。在給出幾個點的坐標求另一個點位置時，一般有兩種方法：第一種是根據已知點的坐標，先作出原點，畫出完整的平面直角坐標系，再觀察點的橫坐標、縱坐標，根據正負性判斷點所在象限，確定具體位置；第二種是對比已知點和未知點的橫坐標、縱坐標的大小，將點進行適當平移，確定具體位置。但這兩種方法都必須建立在已知平面直角坐標系單位長度的基礎上，因此解決此題的關鍵是結合坐標和實際距離確定單位長度。

已知點A和點B的坐標分別是（2，2）和（8，1），分別過點A、B水平向左作兩條豎直直線的垂線，垂足為D、E，由于A、B兩點縱坐標分別為2和1，那么D、E間的豎直距離為1個單位長度，用刻度尺測量出實際距離為0.5厘米，即可得出縱軸上一個單位長度為0.5厘米。……