基于支持向量回歸的盾構隧道巖土參數反演方法

數值模擬技術特別是有限元模擬是預測地表沉降的重要工具。為了提高數值模擬的有效性，文章提出了一種基于支持向量回歸代理模型的盾構隧道巖土參數反演方法，使用該支持向量回歸代理模型替代有限元模型，可提高計算效率；基于代理模型與現場監測數據構建控制方程，使用優化算法PSO求解最佳巖土參數，并通過算例驗證了所提方法的有效性。

盾構掘進；參數反演；沉降預測；支持向量回歸

U455.43A361174

作者簡介：

胡大歡（1994—），助理工程師，主要從事工程建設管理工作。

0" 引言

盾構法是修建地鐵隧道最常見的施工方法，在城市區域修建地鐵隧道時，會經常遇見下穿既有建構筑物的情形。由于盾構施工會引起地表沉降，這會給既有建構筑物帶來很大的風險，因此，預測盾構施工引起的地表沉降是盾構力學中非常重要的步驟。

傳統的盾構掘進地表沉降預測方法包括Peck公式［1-2］經驗法和解析方法［3］。但是這些方法不能考慮復雜的盾構施工過程，也不能考慮巖土介質的非線性等特性。隨著計算技術的發展，數值方法特別是有限元方法已成為預測盾構隧道地表沉降的重要方法，例如，Xie等［4］基于Flac 3D軟件研究了大直徑盾構隧道在上海軟土地區掘進引起的地表沉降規律，并分析了注漿壓力、掌子面支撐壓力等施工參數對地表沉降的影響。Zhang等［5］基于ABAQUS軟件分析了雙線盾構隧道掘進引起的地表沉降規律。徐干成等［6］以北京地鐵14號線馬永區間盾構隧道為背景，研究了盾構下穿對高速鐵路的影響，并提出了注漿可以有效控制盾構掘進引起的鐵路不均勻沉降的觀點。陶連金等［7］基于數值模擬方法分析了新建盾構隧道對已有盾構隧道的影響，發現緊鄰盾構施工會對已有隧道產生縱向效應。上述研究都驗證了數值模擬方法是研究盾構隧道力學的重要工具，可以用來預測盾構掘進引起的地表沉降力學問題。

然而，由于巖土介質具有隨機性，直接基于勘測資料開展的數值計算分析結果一般難以與現場的監測數據相匹配，因此，基于現場的監測數據進行巖土參數的反演分析并不斷更新巖土參數是提高數值結果可靠性的重要方法。在這方面，Kavanagh等［8］、Sakura等［9］提出了基于現場觀測的巖土參數更新方法。此外，鄭亞飛等［10］、劉杰等［11］、賈善坡等［12］都提出了基于有限元的巖土參數反演方法。但是，這些方法并不能直接應用于盾構隧道掘進過程的參數反演，仍然存在著計算繁瑣、計算精度不高的問題。

巖土參數反演問題可以視為一類反分析問題，往往需要不斷地調用有限元數值模型進行前向數值計算。為了提高計算效率，本文提出了一種基于支持向量回歸的盾構隧道巖土參數反演分析方法。該方法具體包含了以下三個部分：（1）基于有限元程序構建隨機輸入/輸出樣本；（2）利用輸入/輸出樣本訓練代理模型，代理模型的構建基于支持向量回歸算法實現；（3）在獲取監測數據的基礎上，利用粒子群優化算法求解控制方法，獲取最佳巖土參數。本文通過一個數值算例驗證所提方法的有效性。

1" 基于SVR代理模型的巖土參數反演分析框架

為了提高盾構掘進引起地表沉降預測結果的有效性，使用現場監測數據反演巖土參數是提高數值計算結果有效性的常見方法。參數反演可以表示為式（1）所示的優化問題：

m（θ）=argminx（‖fpred（x）-fmea‖）（1）

式中：x——待反演的巖土參數；

fpred（x）——數值計算的預測值；

fmea——現場監測的測量值，一般使用地表位移作為反演的數據來源；

‖·‖——向量的距離范數。

在式（1）所示的優化問題中，需要頻繁調用數值模型進行正演計算，這會帶來很大的計算成本。為了提高計算效率，在本文中采用代理模型替代計算成本高昂的有限元模型進行前向分析計算。代理模型的本質是數據驅動算法，其可在給定輸入參數的前提下快速獲得巖土系統的響應值。為了訓練代理模型，需要通過采樣方法（例如超立方拉丁采樣）在給定的巖土參數空間中生成輸入參數樣本，樣本的數量取決于所需的元模型精度和元模型的規模，然后通過有限元模擬獲得相應的輸出值。在本文中使用支持向量回歸（Support Vector Regression，以下簡稱SVR）算法構建代理模型。

1.1" SVR算法

對于一組訓練樣本{（x（1），y（1）），…，（x（l），y（l））}，SVR定義了如式（2）所示的優化問題：

Minimise J（w，e）=12wTw+C2∑li=1e（i）2

Subject to y（i）=wTφ（x（i））+b+e（i）2，e（i）gt;0，i=1，2，…，l（2）

式中：w——參數向量；

b——偏置參數；

C——正則化參數；

e（i）——第i個訓練樣本的誤差；

φ（x（i））——非線性映射函數。

引入拉格朗日乘子向量α，可以得到式（3）所示的拉格朗日函數：

L（w，b，e，α）=J（w，e）-∑li=1α（i）［wTφ（x（i））+b+e（i）-y（i）］（3）

根據KKT條件，可以得到L關于w、b、e、α的偏導數并得到如下所示的方程組：

0" 1T1" Q+C-1Ibα=0y（4）

式中：1=［1，1，…，1］T，I——單位矩陣，維度為l。y=［y（1），y（2），…，y（l）］T，Q=［qij］l×l，qij=K（x（i），x（j））。

K（x（i），x（j））——核函數。

核函數的選擇有很多種，包括：徑向基核函數（rbf）、線性核函數（linear）、多項式核函數（polynomial），如式（5）所示：

K（x（i），x（j））=〈x（i），x（j）〉linear

K（x（i），x（j））=（γ〈x（i），x（j）〉+r）dpolynomial

K（x（i），x（j））=exp（-γ‖x（i）-x（j）‖2）rbf（5）

式中：〈·，·〉——向量內積；

r——系數；

d——核函數維度；

γ——＞0的超參數。

將式（4）進一步擴展可以得到：

0""" 1" """"""1""" …""" 1

1K（x（1），x（1））+1C" K（x（1），x（1））" …" K（x（1），x（l））

1" K（x（2），x（1））" K（x（2），x（2））+1C…" K（x（2），x（l））

"""""" ""

1" K（x（l），x（1））" K（x（l），x（2））" …K（x（l），x（l））+1C

b

α（1）

α（2）

α（l）=

0

y（1）

y（2）

y（l）

（6）

令ξ=（Q+C-1I）-1，則b和α可以通過求解線性方程組得到，結果為：

b=1Tξy1Tξ1（7）

α=ξ（y-11Tξy1Tξ1）（8）

因此，SVR的預測結果可以表示為：

f（x）=∑li=1α（i）K（x（i），x）+b（9）

基于支持向量回歸的盾構隧道巖土參數反演方法/胡大歡

1.2" 控制方程的建立與求解

在完成代理模型的構建后，控制方程式（1）可以轉化為如下形式：

m（x）=argminx∑ni=1（fi（x）-fmeai）2（10）

式中：n——地表監測點的數量。

為了求解式（10），需要使用優化算法，在本文中采用粒子群優化算法（PSO）。該算法的核心思想是模擬鳥類的搜索食物的行為，初始化一群粒子，每個搜索粒子都代表了解空間的一組候選解，根據每個粒子的當前位置和當前速度，計算每個粒子的函數值，并基于所有粒子的全局最優位置和個體最優位置更新，直至滿足迭代次數或者搜索條件。粒子的速度和位置更新公式為：

v（t+1）ij=wv（t）ij+c1r1（pij-x（t）ij）+c2r2（pgj-x（t）ij）

x（t+1）ij=x（t）ij+v（t+1）ij（11）

式中：v（t+1）ij——第i個粒子在第（t+1）次迭代時的第j維度的速度；

x（t）ij——第i個粒子在第（t）次迭代時的第j個維度的位置；

pij——第i個粒子的個體最優位置；

pgj——所有粒子的全局最優位置；

w——慣性權重；

c1和c2——加速因子；

r1和r2——隨機數。

1.3" 參數反演框架

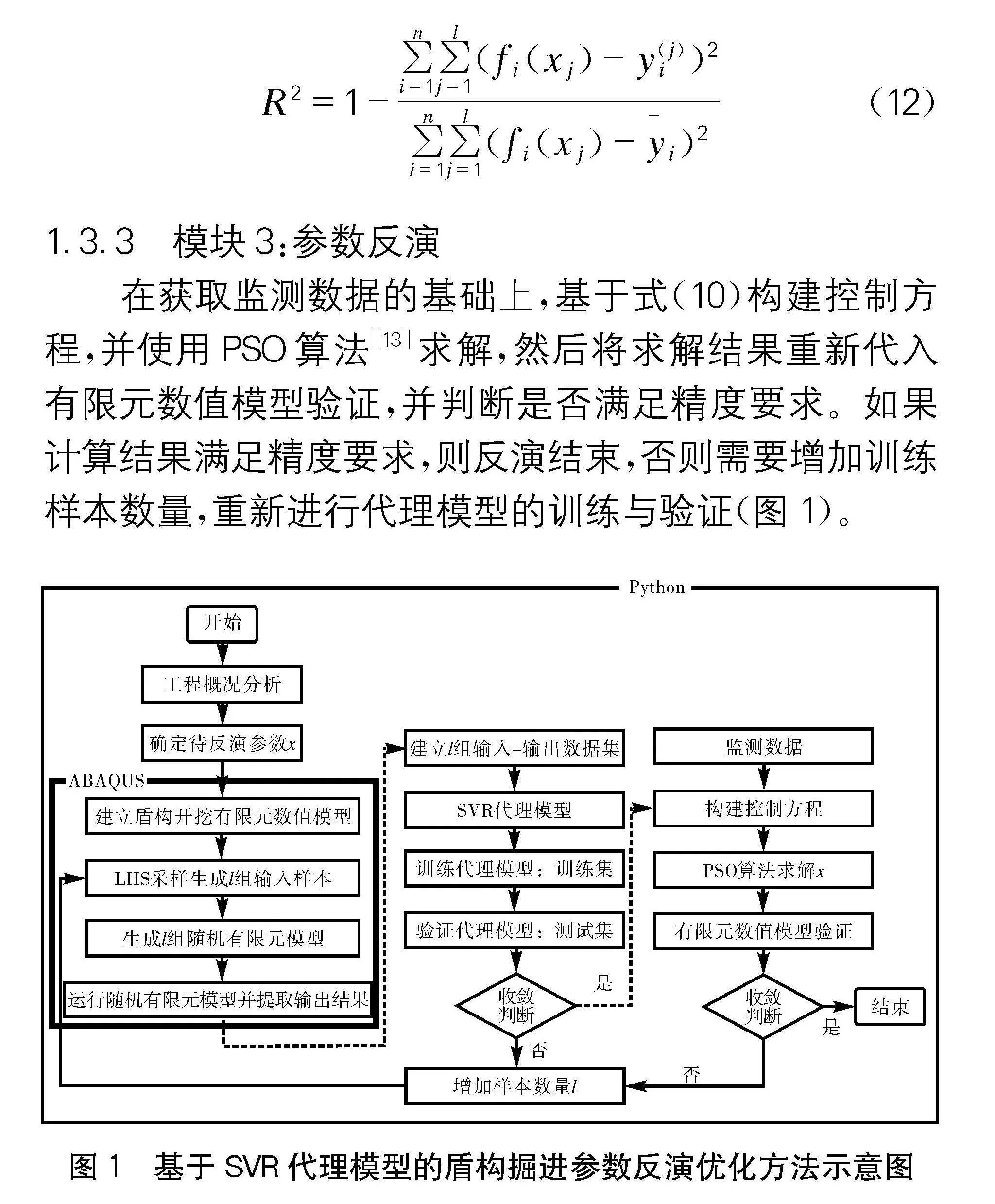
本文提出基于SVR代理模型的反演框架，所提參數反演算法基于Python編程語言實現。該框架具體包含了三個模塊：

1.3.1" 模塊1：基于ABAQUS的隨機有限元模型的建立

為了訓練代理模型，需要生成l組輸入/輸出樣本。基于超立方拉丁采樣LHS算法生成l組輸入樣本；建立盾構施工的標準有限元模型，并導出standard.inp文件，其中.inp代表ABAQUS的標準輸入文件；通過修改.inp文件的關鍵字生成l組隨機有限元模型；運行l組隨機有限元模型，并提取對應模型的節點位移，即為輸出數據集。

1.3.2" 模塊2：代理模型的訓練與驗證

在獲取l組訓練樣本的基礎上，將這l組訓練樣本按8∶2的比例劃分為訓練集和測試集。使用訓練集的樣本擬合SVR代理模型，計算過程如式（2）～（9）所示。使用測試集的樣本驗證SVR代理模型，代理模型的計算精度通過回歸系數R表達，如式（12）所示。如果代理模型滿足精度要求，則進入下一階段，否則需要增加訓練樣本數量，重新進行代理模型的訓練與驗證：

R2=1-∑ni=1∑lj=1（fi（xj）-y（j）i）2∑ni=1∑lj=1（fi（xj）-y-i）2（12）

1.3.3" 模塊3：參數反演

在獲取監測數據的基礎上，基于式（10）構建控制方程，并使用PSO算法［13］求解，然后將求解結果重新代入有限元數值模型驗證，并判斷是否滿足精度要求。如果計算結果滿足精度要求，則反演結束，否則需要增加訓練樣本數量，重新進行代理模型的訓練與驗證（圖1）。

圖1" 基于SVR代理模型的盾構掘進參數反演優化方法示意圖

2" 算例驗證

2.1" 模型簡介

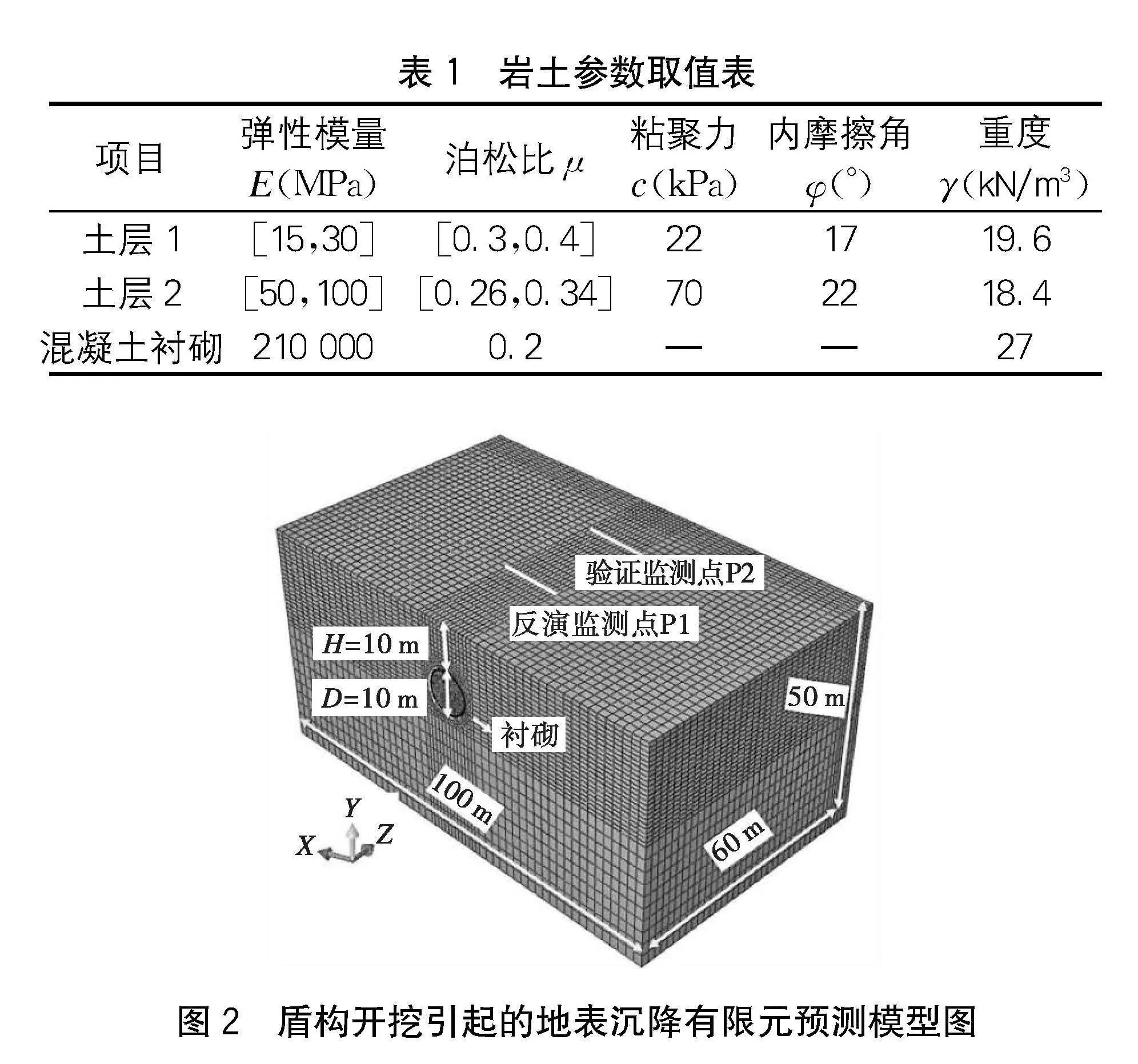
本文通過一個算例驗證所提方法的有效性。在該算例中，盾構隧道直徑D=10 m，隧道埋深H=10 m，土層包含土層1和土層2，兩個土層的厚度分別為3 m和47 m，襯砌厚度為0.35 m，盾構掘進過程中的注漿壓力和掌子面支撐壓力分別為0.1 MPa、0.1 MPa。建立如圖2所示的有限元數值模型，數值模型尺寸為X×Y×Z=100 m×50 m×60 m。土層采用C3D8R單元，襯砌采用C3D8I單元類型。土層和襯砌的六面體單元數量分別為85 605和9 984。土體和襯砌分別采用摩爾-庫侖和線彈性本構。為了提高計算效率，每環盾構掘進設置為5 m，共模擬了盾構掘進12環。

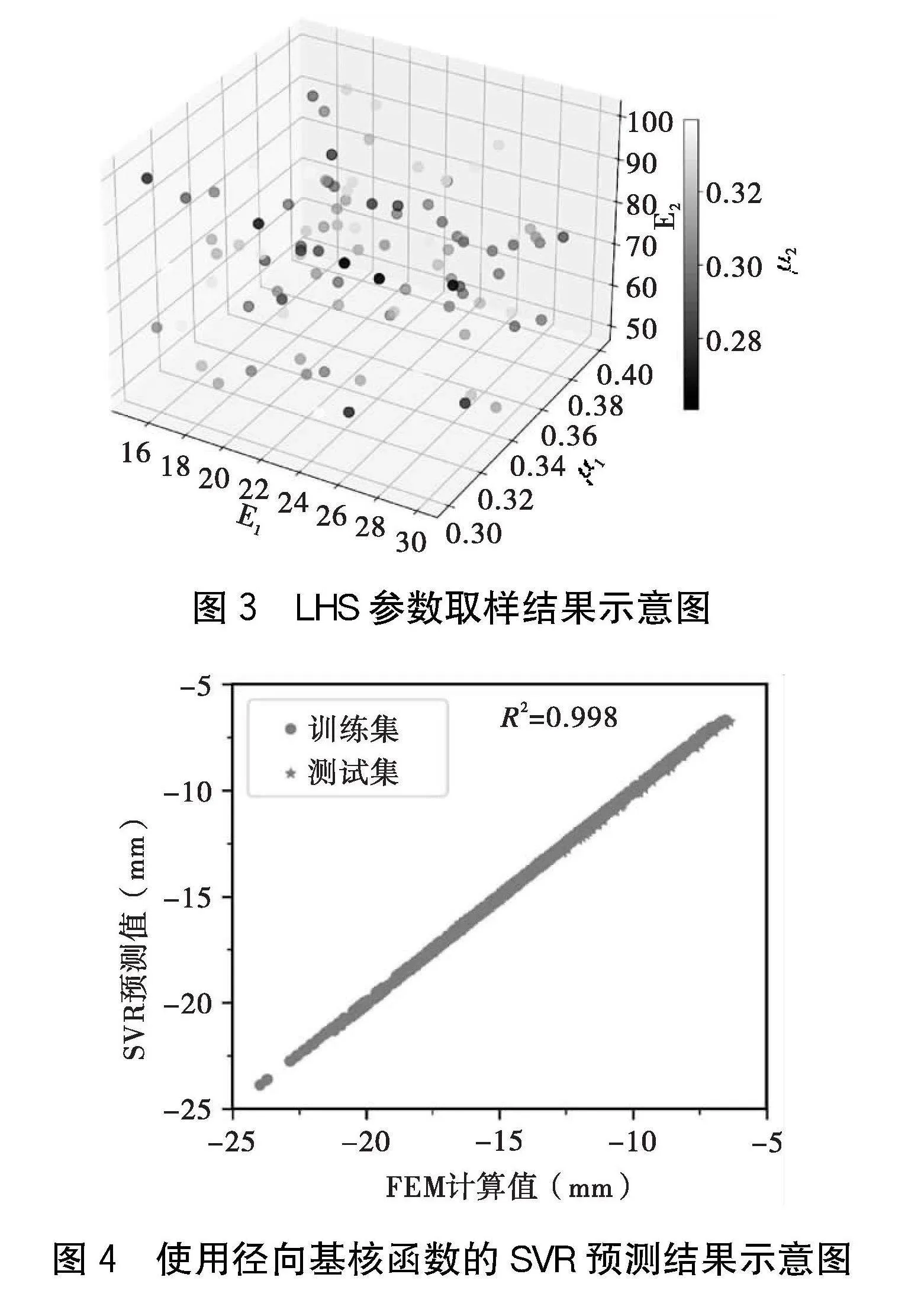
使用地表的監測位移反演優化巖土參數，考慮到位移反演主要受材料的剛度參數影響，因此在本問題中，考慮土層1和土層2的彈性模量E和泊松比μ為待反演參數，土層的重度γ、粘聚力c和內摩擦角φ視為固定值。參數的取值范圍如表1所示。

2.2" 代理模型訓練與驗證

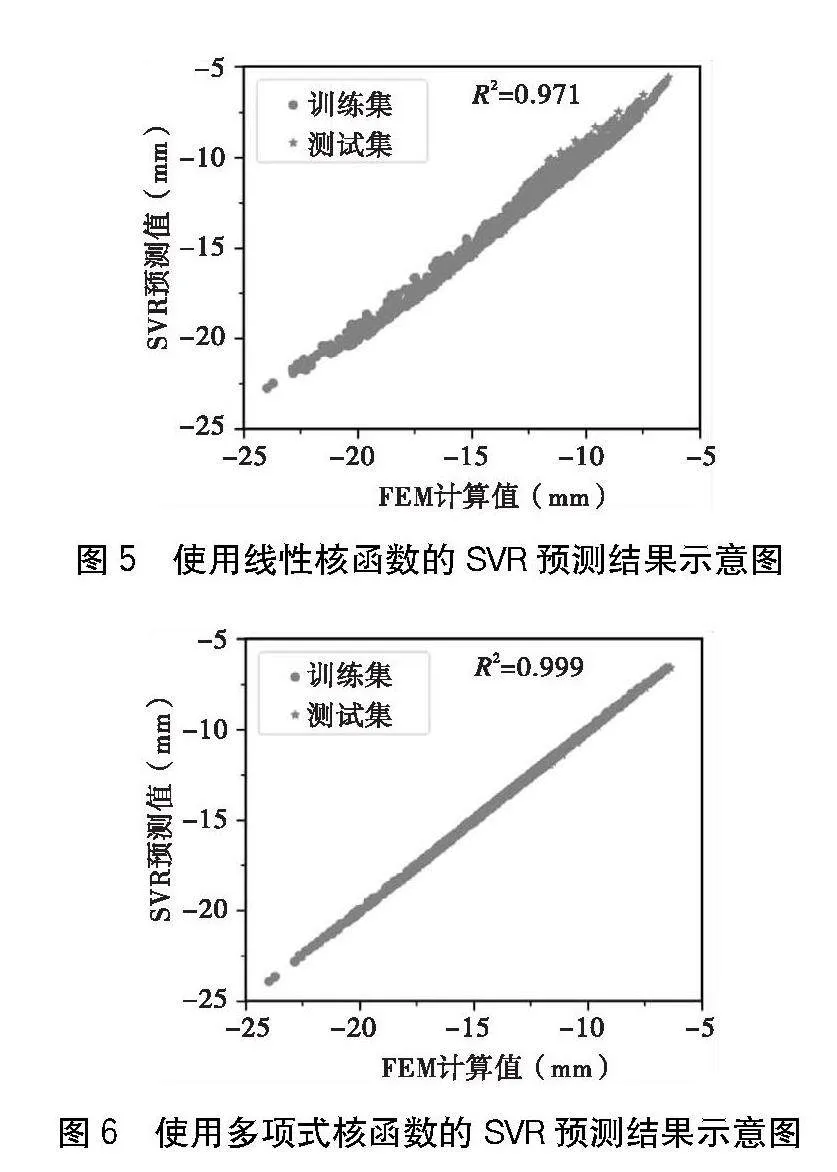
為了訓練SVR代理模型，生成了100組隨機有限元模型，即圖1中的參數l=100。使用超立方拉丁抽樣算法LHS生成了100組輸入參數，E1、μ1、E2和μ2的分布如圖3所示。使用Python語言編寫ABAQUS軟件批量計算腳本并提取地表沉降，生成輸入/輸出數據集，將數據集按8∶2劃分為訓練集和測試集，分別使用徑向基核函數、線性核函數和多項式核函數訓練SVR代理模型，所訓練代理模型在訓練集和測試集上的預測結果分別如圖4和下頁圖5～6所示。三個模型的回歸系數R2分別為0.998、0.971、0.999。可以看到，代理模型在訓練集和測試集上的精度非常高，因此可以替代反演需要的有限元模型，提高計算效率。

2.3" 巖土參數反演

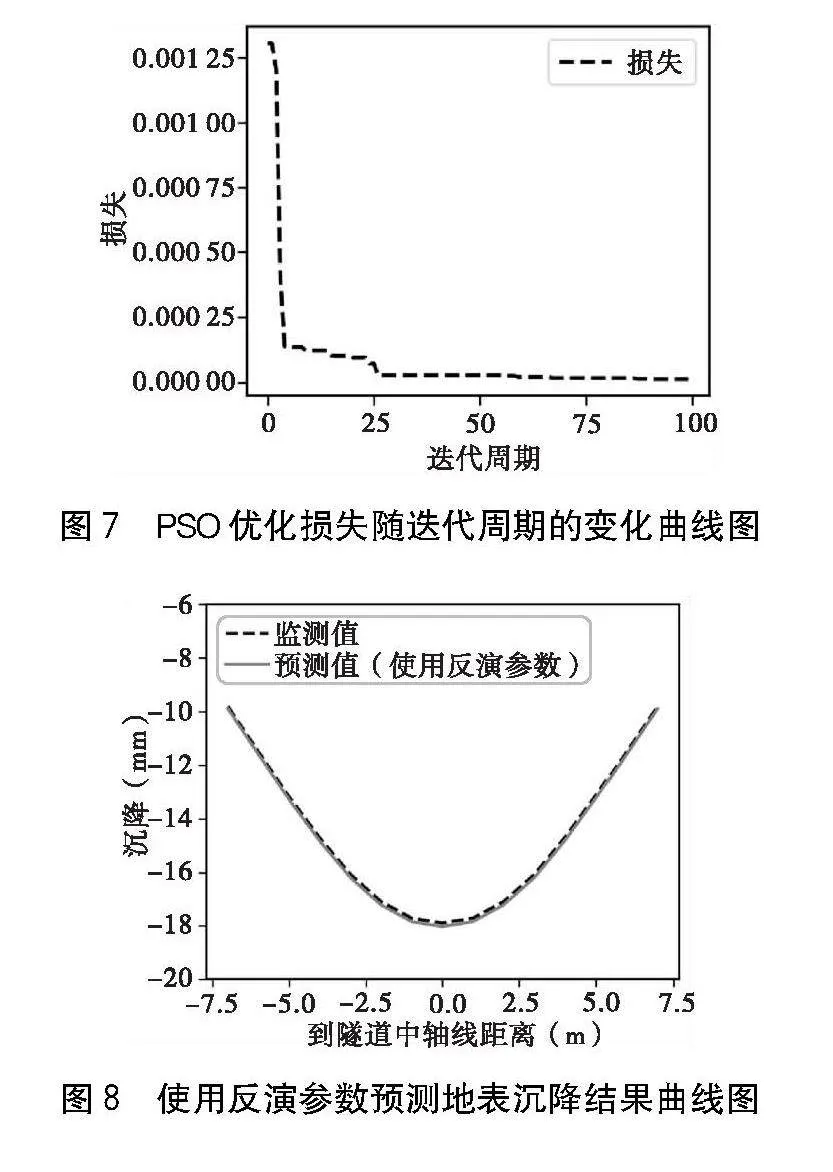
在本算例中，使用偽測量值作為參數反演的地表位移數據來源，偽測量值可以通過運行一組固定巖土參數x的有限元模型得到。如圖7所示給出了使用PSO優化損失隨迭代周期的變化圖，最終損失cost收斂至1.26e-5，巖土參數的反演結果為x=［23.11，0.37，75.80，0.27］T，即E1=23.11 MPa，μ1=0.37，E2=75.80 MPa，μ2=0.27。

為了驗證參數反演結果的有效性，將參數反演結果重新代入有限元模型進行前向計算，并提取驗證點位的地表沉降，測量值結果與預測結果如圖8所示。由圖8可知，使用反演參數預測的地表沉降結果與監測值是非常貼近的。

3" 結語

預測盾構掘進引起的地表沉降是盾構隧道力學中的重要問題。數值方法是預測盾構掘進引起的地表沉降的重要工具。為了提高數值模擬的有效性，本文提出了一種基于支持向量回歸代理模型的盾構隧道巖土參數反演方法。在所提反演框架中，基于LHS采樣生成了一組隨機輸入參數，并生成隨機有限元模型，用于構建輸入輸出數據集，然后基于數據集訓練并驗證SVR代理模型。最后，基于監測數據和SVR代理模型建立控制方程，并使用PSO算法求解最佳巖土參數。同時，通過一個算例驗證了所提方法的有效性。得出結論如下：

（1）分別使用徑向基核函數、線性核函數和多項式核函數構建代理模型，三種代理模型在數據集上的回歸系數R2分別為0.998、0.971、0.999，說明多項式核函數構建的代理模型精度最高，適合作為后續反演的核函數。

（2）使用優化后的巖土參數預測地表沉降值與監測數據非常貼近，這說明使用更新優化后的參數進行數值計算可以極大地提高數值模擬的有效性。

［1］Peck R B.Advantages and limitations of the observational method in applied soil mechanics［J］.Geotechnique，1969，19（2）：171-187.

［2］Peck R B.Deep Excavations and Tunneling in Soft Ground，State of the Art Report［C］.Proe.7Int.Conf.on Soil mechanics and Foundation Engineering， mexico City，1969.

［3］Xie J，Li P，Zhang m，et al.Analytical solutions of ground settlement induced by yaw in a space curved shield tunnel［J］.Underground Space，2023（13）：86-103.

［4］Xie X，Yang Y，Ji m.Analysis of ground surface settlement induced by the construction of a large-diameter shield-driven tunnel in Shanghai，China［J］.Tunnelling and Underground Space Technology，2016（51）：120-132.

［5］Zhang Z X，Liu C，Huang X，et al.Three-dimensional finite-element analysis on ground responses during twin-tunnel construction using the URUP method［J］.Tunnelling and Underground Space Technology，2016（58）：133-146.

［6］徐干成，李成學，王后裕，等.地鐵盾構隧道下穿京津城際高速鐵路影響分析［J］.巖土力學，2009，30（S2）：269-272，276.

［7］陶連金，孫" 斌，李曉霖.超近距離雙孔并行盾構施工的相互影響分析［J］.巖石力學與工程學報，2009，28（9）：1 856-1 862.

［8］Kavanagh K T，Clough R W.Finite element applications in the characterization of elastic solids［J］.International Journal of Solids and Structures，1971，7（1）：11-23.

［9］Sakurai S，Takeuchi K.Back analysis of measured displacements of tunnels［J］.Rock mechanics and rock engineering，1983，16（3）：173-180.

［10］鄭亞飛，張璐璐，于永堂，等.基于Pareto最優的地基位移多目標反分析［J］.土木工程學報，2015（S2）：214-219.

［11］劉" 杰，王" 媛，劉" 寧.巖土工程滲流參數反問題［J］.巖土力學，2002（2）：152-161.

［12］賈善坡，伍國軍，陳衛忠.基于粒子群算法與混合罰函數法的有限元優化反演模型及應用［J］.巖土力學，2011，32（S2）：598-603.

［13］Eberhart R，Kennedy J.A new optimizer using particle swarm theory［C］.MHS′95.Proceedings of the Sixth International Symposium on micro machine and Human Science.Ieee，1995.

20240407