基于Python的數學分析課程可視化和計算教學探索

關鍵詞：數學分析；課程教學；Python語言；可視化；計算

0 引言

數學實驗旨在利用軟件編程的方式提高科學計算問題的能力，其特點在于增強學習過程的可視性、嘗試性和再創性[1]。過去二十多年間，Matlab[2]、Maple[3]和Mathematica[4]等數學軟件在教學中得到廣泛的應用，并取得了良好的效果。然而，這些軟件雖功能強大但價格昂貴，大多數普通高校和科研人員承擔不起[5]。因此，選用開源的Python作為數學實驗課程的輔助軟件是明智之舉[6]。Python是目前常用的編程語言之一，具有很強的生命力[6]。Python語言以其簡單易學、面向對象、免費開源等特點著稱[7]，并擁有豐富的第三方庫支持，可應用于數據分析、機器學習、人工智能等多個領域[6]。

1 基于Python 的數學分析課程實驗教學的意義

數學分析是古典微積分的核心內容，是學習專業基礎課、專業課的一塊基石，在科學技術中有廣泛應用。通過學習，提高學生的邏輯推理能力、抽象思維能力及計算能力，增強基本技能，擴大視野，陶冶情操，進而提高數學素質與數學修養。然而，當前數學分析課程教學普遍存在授課形式單一、學生學習興趣不高等問題。數學分析課程內容抽象復雜，部分學生難以理解，甚至產生畏難情緒。因此，有必要積極探索新的教學思路和方法，以提升教學效果。借助Py?thon進行可視化實驗和復雜問題計算，可以使學生的理解更加直觀，提高學習積極性[8]。

1.1 Python 編程成為必備技能

隨著大數據、人工智能等技術的快速發展，編程技能已成為相關領域從業人員的必備技能[6]。目前，我校所有理工類專業均開設Python程序設計課程，對學生進行編程教育。在數學分析教學中若融入Py?thon的可視化、仿真和建模等，不僅使學生對相應的數原理的思考更深入透徹，而且對學生提高動手實踐能力方面也有幫助。

1.2 改善理論教學枯燥性

傳統教學模式下，教師難以兼顧所有學生的個體差異，容易導致部分學生學習積極性不高。Python語言的圖像功能有助于學生減輕學習畏難心理，加強理解和對比。圖形可視化可以將抽象的數學概念以更直觀、有趣的方式呈現，激發學生的學習興趣，同時也有助于教師兼顧不同學生的學習需求。

1.3 提升數學建模能力

數學課程教學普遍注重理論知識的講解，而忽視與實際應用的結合，導致學生缺乏感性認識。利用Python軟件進行數學建模，可以培養學生的建模意識和編程能力，并幫助他們解決實際問題。這不僅使得課堂教學更生動形象，也會提升學生解決實際問題的能力。同時，學生數學建模能力也將得到進一步提升，向專業更深領域發展。

2 基于Python 的可視化和計算教學案例

本節將通過典型案例，介紹如何利用Python 的SymPy、Math、SciPy、NumPy、Matplotlib 等第三方庫進行函數繪圖、極限計算、導數和積分計算等操作。案例實驗環境是Windows11+Python3.9，所用函數來自華東師范大學編寫的《數學分析》教材（第五版）[9]。

2.1 繪制圖像

Python可以繪制二維和三維圖形，例如一元函數的二維圖像、二元函數的三維圖像以及空間曲線等。

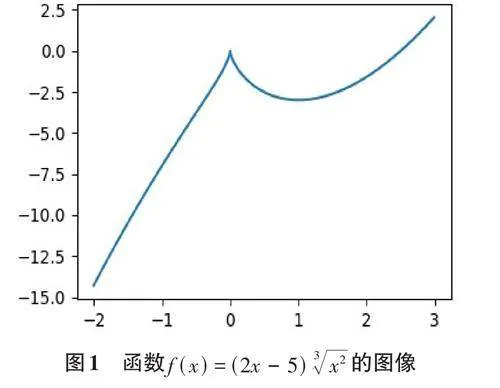
例 1：繪 制 f （x） = （2x - 5） 3 x2 在 [-2，3] 上 的圖形。

2.2 了解函數分布

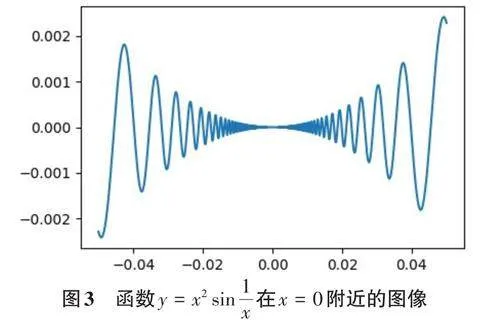
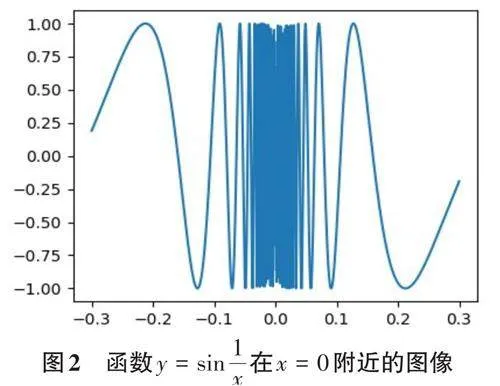
函數極限的概念較為抽象，部分學生難以理解。以涉及無窮大、無窮小和有界函數的極限為例，傳統的板書和語言描述難以清晰地展現函數的變化趨勢，而Python的可視化功能可以彌補這一缺陷，幫助學生直觀地理解極限的概念。

結果展示如圖2， 當x → 0時，函數值在區間[-1，1] 來回振蕩，越接近0，振蕩頻率越高，但并不趨于0。從圖像看，越來越快地振蕩而不停止，故可理解不存在極限。

2.3 計算極限

求極限的命令是limit（f，x，x_0，dir） ，其四個參數分別是：函數或數列極限表達式，極限的變量，變化的趨勢和極限的方向。dir =‘+ ’， dir =‘ -’分別表示右、左極限。注意：Python符號運算時應先加載數學符號函數庫SymPy。

2.4 計算導數或偏導數

求微分關鍵是求導，此處僅討論求解函數導數，可以利用SymPy包的命令diff來完成，語法是： diff（f，x，alpha） ，其中f為求導函數，x 為自變量，alpha為求導的其他設置，如階數等。很多時候，自變量還有特定的值，可以進行表達式代入值的求導，這時需要定義函數，通過evalf方法傳入x 的數值。

2.5 計算函數的積分

在Python中，使用SymPy包可以計算微積分，主要通過integrate方法計算，語法是： integrate（f，（x，a，b）），其中f為被積函數，x為自變量，a，b分別為上、下限。

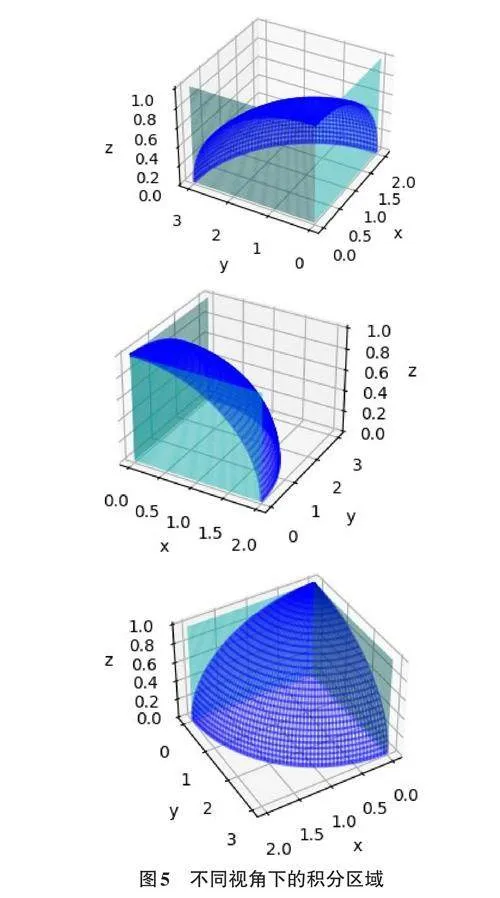
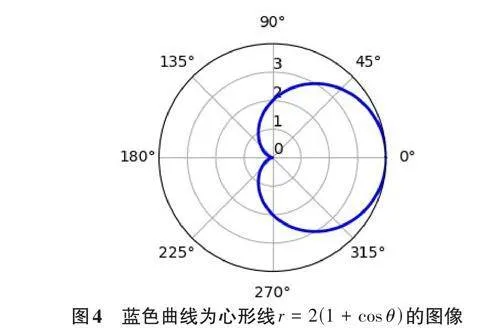
對于比較復雜的積分，部分學生缺乏空間想象力或繪圖能力，難以繪制積分相關圖形，找不到積分區域或積分限。有些學生則對積分公式或方法掌握不牢，無法或很難計算。以下通過心形線的例子，計算心形線長度及其所圍面積。

例9： 已知心形線r = 2（1 + cosθ ），求它的弧長和所圍圖形的面積。

2.6 計算曲線積分和曲面積分

由于Python目前缺乏直接計算曲線積分和曲面積分的函數，通常需要利用數學公式將其轉換為定積分或二重積分進行求解。曲線積分所對應的定積分被積函數往往較為復雜，可以使用 SciPy 庫的 inte?grate.quad（） 函數進行計算。類似地，曲面積分所對應的二重積分可以使用 integrate.dblquad（） 函數進行計算。

3 結論

Python 語言應用廣泛，幾乎涵蓋了所有程序領域，被譽為“膠水語言”。自2013年起，越來越多的高校開始面向非計算機專業開設Python語言編程課程。上述分析和案例實踐表明，Python 軟件可以有效輔助數學分析課程教學，幫助學生理解抽象的理論知識，并將其應用于解決實際問題。盡管Python在計算復雜積分等方面仍有提升空間，但其作為一款免費開源軟件，擁有強大的社區支持和持續更新的能力，未來發展潛力巨大。本文探討了Python在數學分析實驗教學中的應用，旨在幫助學生更好地理解和應用所學知識，并掌握 Python的編程思想。在未來就業市場中，數學專業畢業生需要具備一定的計算機和軟件操作能力。因此，將Python融入數學專業課程教學，是順應時代發展趨勢、提升人才培養質量的必然選擇。