基于人工蜂群算法的冗余機械臂逆運動學求解

摘要：利用D-H法對冗余機械臂建立運動學模型，通過坐標系的轉換得出正運動學的解；探討人工蜂群算法對7DOF機械臂運動學求解的有效性，使用人工蜂群算法對冗余機械臂進行逆運動學求解，構造以位置誤差以及求解時間為目標函數來尋求最優解；以最小位置誤差和求解時間為目標，讓機械臂運行到指定位置并將計算結果與粒子群算法進行比較。Matlab仿真實驗表明：人工蜂群算法所計算的位置誤差穩定在10-4mm，其搜索精度、收斂精度以及收斂速度均優于粒子群算法，計算最優解所使用的時間也優于粒子群算法，所表現的穩定性以及魯棒性更適用于冗余機械臂的逆運動學求解。

關鍵詞：逆運動學求解；人工蜂群算法；粒子群算法；收斂精度

中圖分類號：TP241; TP18文獻標志碼：A文章編號：1671-5276（2024）06-0218-06

Abstract：A kinematics model is established by D-H method， and the forward kinematics solution is obtained through the transformation of coordinate system. The validity of artificial bee colony algorithm for kinematics solution of 7DOF manipulator is discussed. The inverse kinematics of the redundant manipulator is solved by using the artificial bee colony algorithm， and the optimal solution is found by constructing the objective function of position error and solution time. The minimum position error and solution time are taken as the objectives to make the manipulator run to the specified position and compare the calculation results with the particle swarm algorithm. The Matlab simulation experiment shows that the position error calculated by the artificial bee colony algorithm is stable at 10-4mm， and the search accuracy， convergence accuracy and speed of the artificial bee colony algorithm are better than particle swarm algorithm， and the stability and robustness of the algorithm are more suitable for the inverse kinematics solution of redundant manipulator.

Keywords：inverse kinematics solution; artificial bee colony algorithm; particle swarm algorithm; convergence precision

0引言

隨著科技的快速發展，工業現代化的發展越發快速，目前機械臂在各個領域中應用越發多樣化，在航天領域、汽車領域以及精密制造等領域中都承擔著重要的功能。7自由度機械臂的主要功能包括實現本體避障、奇異位形回避、避限位關節、關節力矩優化以及增加操作性等［1］。與傳統的6自由度機械臂相比，7自由度機械臂的特點就是多了一個冗余自由度，其使用結構與人類的手臂更為相近。然而，7自由度機械臂的關節角變量更多，導致其逆運動學求解的過程也更加繁瑣復雜。當前，用于求解冗余機械臂逆運動學問題的方法主要有3種：封閉解法、數值解法以及智能求解法［2］。

封閉解法的使用原理為采用空間幾何知識對機械臂進行逆運動學求解，其求解結果精確，計算時間快。但是該方法主要適用于滿足Pieper準則的機械臂結構，而冗余機械臂由于關節角變量過多，使用該方法求解過程極其困難，計算結果誤差較大。數值解法使用原理為采用雅可比矩陣法、梯度投影法等方法進行求解［3］。雅可比矩陣法的工作原理就是通過不斷地求導計算以及求逆計算來得到求解答案；梯度投影法的工作原理就是通過梯度的投影技巧來求逆運動學解的近似值。智能求解法的使用原理為通過編碼以及適應度函數的設置將逆運動學求解過程轉換成尋優過程，目前市場上對于逆運動學求解的算法主要包括神經網絡、粒子群算法、遺傳算法等等。文獻［4］通過使用人工蜂群算法對冗余機械臂進行逆運動學求解，以位置誤差以及位姿誤差作為優化標準的判斷。文獻［5］通過將布谷鳥算法以及帝國主義競爭算法融合使用，提升了算法的搜索性能，并將其運用到機械臂的逆運動學求解過程中。相對于傳統的啟發式算法而言，混合算法在搜索空間最優解中具備較大優勢，是目前研究的主要方向之一。

本文基于軟塑料育苗營養缽的缽苗移栽機構設計，通過使用機械臂自動移栽已成型的林木苗袋缽苗到缽體之內，因此在移栽的過程中需要保證機械臂的位置精度。本文通過研究冗余機械臂的逆運動學求解方法，建立以位置誤差以及姿態誤差為目標的函數方程，通過使用人工蜂群算法進行逆運動學求解，并將其與粒子群算法的求解結果進行比較，展示人工蜂群算法的優秀性能，保證機械臂移栽的位置準確性。

1機械臂的逆運動學建模

1.1機械臂介紹

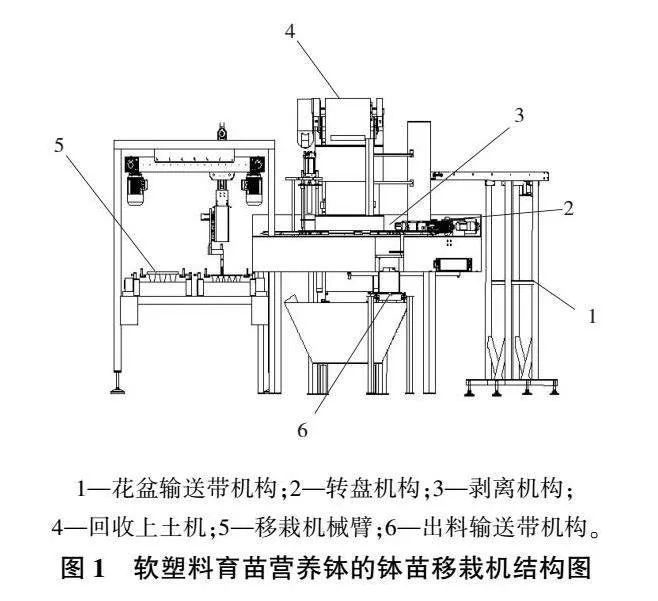
基于軟塑料育苗營養缽的缽苗移栽機構結構如圖1所示。

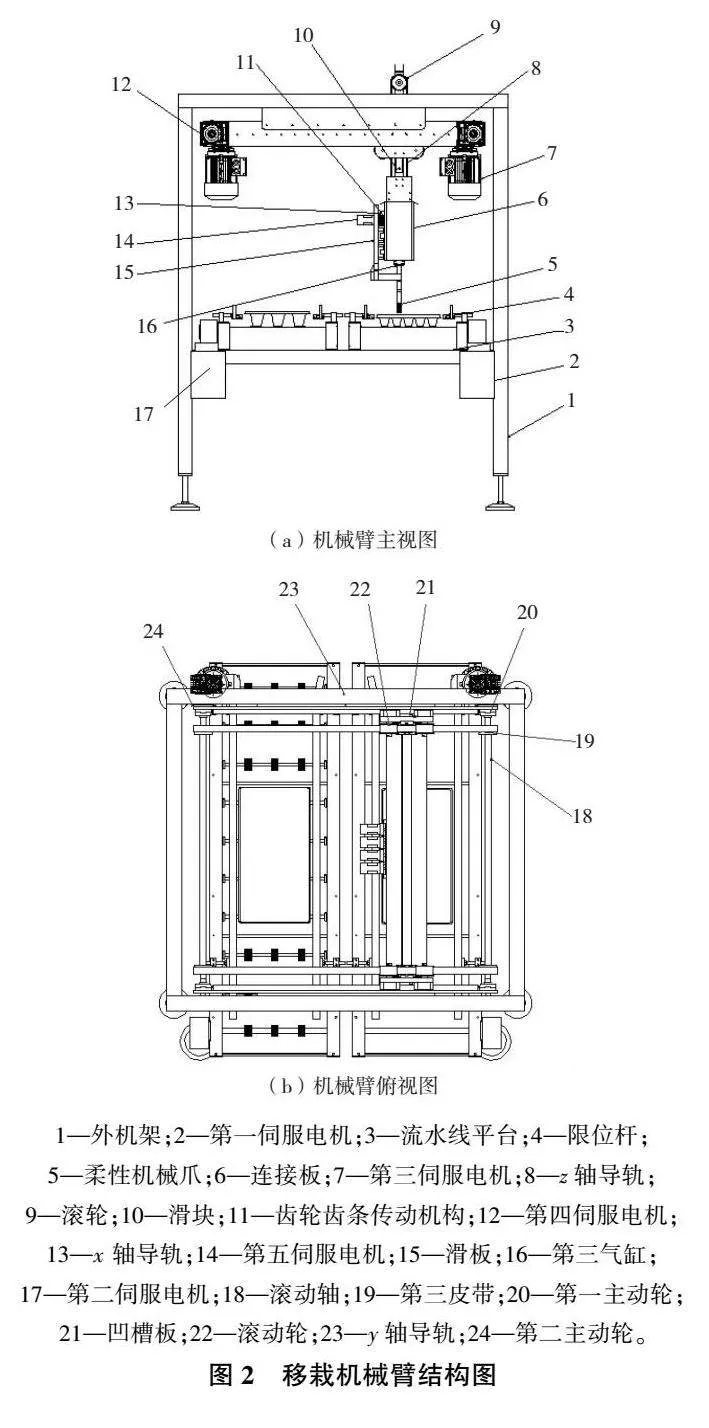
移栽機械臂主要依靠雙電機驅動，通過皮帶、滾輪帶動x、y、z軸導軌進行空間移動，移栽機械臂的末端執行機構內通過氣缸的控制對林木苗袋苗進行缽體移栽，其移載機械臂的結構如圖2所示。

本次設計的機械臂為7自由度冗余機械臂，其中自由度主要由外機架與機械臂兩個部分所組成，其中外機架的3個自由度主要為第一伺服電機2控制的流水線平臺3，從而進行流水線平臺y方向的移動，實現育苗盤的輸送工作；第二伺服電機17控制外機架z方向的移動，實現外機架的高度調節工作；限位桿4通過調節控制外機架x方向的移動實現不同規格育苗盤的使用。機械臂的4個自由度控制為第三伺服電機7以及第四伺服電機12控制y軸導軌23以及z軸導軌8移動，完成z方向與y方向的移動。另外第五伺服電機14控制x軸導軌13的移動，完成x方向的移動，實現機械臂無死角抓取功能；最后由第三氣缸16控制柔性機械爪5完成抓取移栽的工作。

上述所涉及的7自由度機械臂主要實現方式是通過電機控制皮帶傳動機構、齒輪齒條傳動機構來完成的。因此為了保證林木苗袋苗在移栽過程中的精度，本文將通過對7DOF機械臂做研究，尋找移栽位置中的最優解，其運動示意圖如圖3所示。

通過對冗余機械臂的關節變量以及基座建立坐標系，將基座坐標系視為坐標原點，設計成Ox0y0z0，轉動關節（1—7）的坐標中設定為Ox1y1z1—Ox7y7z7。圖中對機械臂的各個關節變量處都建立三維坐標系，用以描述機械臂的運動情況［6］。本次冗余機械臂的D-H運動參數以及關節變量范圍如表1所示。表中ai表示連桿長度；αi表示連桿扭角；di表示連桿偏距；θi表示關節角活動范圍，也是設計的搜索范圍。

1.2逆運動學問題與建模

對于冗余機械臂的逆運動學求解原理就是對機械臂的末端執行器設定位姿（xex，yex，zex，αex，βex，γex），求解出該位姿下其所對應的關節空間點θi，i=1，2，…，7最優解。其中（xex，yex，zex）指的是末端執行器的質點在極坐標的位置，（αex，βex，γex）指的是末端執行器在極坐標系的歐拉角［7］。

對于機械臂的逆運動學求解使用傳統的啟發式算法為常見方法，啟發式算法的使用原理就是通過算法建立正運動學方程對機械臂的執行末端進行求解運算，以最小位置誤差以及姿態誤差為目標來尋求最優解。

基于歐拉角法建立坐標軸之間的轉換矩陣，依次對建立的3個坐標軸進行旋轉，每個坐標軸在旋轉時與前后坐標軸呈現正交狀態，在通過平移達到坐標系重合［8］。在平移旋轉的過程中，假設機械臂當下的關節角為θi，i=1，2，…，7，則坐標系i到坐標系i-1的轉換矩陣為

式中Ti-1i為從坐標系i到坐標系i-1的轉換矩陣。

冗余機械臂的末端執行器到基座坐標系的齊次轉換矩陣方程為

式中（px，py，pz）為機械臂末端執行器質心在基座坐標系的實際位置。

根據式（2）所計算的質心實際坐標位置，可以求得機械臂末端執行器的實際姿態位置為

式中（αre，βre，γre）為機械臂末端執行器基座坐標系的實際歐拉角。

根據上面設定的末端機械臂位姿以及關節空間點所求的末端執行器實際位姿，則計算所得的位置誤差以及姿態誤差為

式中：ΔP為機械臂的位置誤差；ΔR為機械臂的姿態誤差。

位置誤差變化主要和連桿長度以及連桿偏距有關，而姿態誤差變化主要和連桿長度有關。由于計算式兩者不屬于同一量綱，所以求解時為了保證兩種誤差盡可能獲得最小值，引入了誤差系數wp、wr，即

式中：wp為位置誤差系數，取值為wp=1；wr為姿態誤差系數，取值wr=180/π，隨機械臂的變化而自行調整。

本次討論的機械臂由于采用的主要控制方式為伺服電機的控制，通過齒輪齒條傳動機構以及皮帶機構完成傳動，其中工作時所受到的慣性以及摩擦力不會影響其控制效果，因此不予考慮。

2使用算法描述

2.1人工蜂群ABC算法

在人工蜂群算法之中，可以將蜜蜂主要分成3類：引領蜂、跟隨蜂以及偵察蜂。人工蜂群算法的過程包括蜜蜂的初始化、引領蜂進行搜索階段，跟隨蜂進行搜索階段，最后是偵查蜂進行搜索階段等。

在初始化階段中，蜜蜂按照隨機方式進行位置的初始化：

式中：i∈［1，N］為蜜蜂的編號；N為蜜蜂的總數量；j∈［1，J］為位置維度；J為位置維度；Xmaxj、Xminj為位置維度J的最大值以及最小值；Xij為蜜蜂的隨機初始化位置。

在引領蜂進行搜索階段搜索食物源時，發現新的搜索途徑可以減少搜索時間，則會使用新的搜索方法。適應度靠前的蜜蜂轉換成引領蜂，后面的蜜蜂轉換成跟隨蜂繼續進行搜索［9］。其中前面的引領蜂位置則發生改變為

式中：Xj為原蜜源位置；X′ij為引領蜂搜索到的新蜜源位置。

引領蜂搜尋到新的蜜源位置進行位置的改變后，會通過信號傳遞給后面的跟隨蜂，跟隨蜂會選擇是否跟隨前面的引領蜂前進，其跟隨概率為

式中：pi為跟隨蜂選擇跟隨引領蜂前進的概率；fit，i=1/f1obj為引領蜂位置適應度數值；f1obj為引領蜂發現蜜源的目標函數。

在跟隨蜂選擇跟隨引領蜂后，蜜蜂就開始一起向蜜源處進行搜索采蜜。在引領蜂與跟隨蜂在蜜源位置進行采蜜搜索，采蜜次數超過了設定值，且蜜源適應度沒有顯著提高，蜜蜂將放棄對該區域的搜索探查，將換成偵查蜂重新進行新蜜源的大范圍搜索：

所以人工蜂群算法的優勢就是可以采用交叉操作在全局尋求最優解，提高了計算的精度。

2.2粒子群PSO算法

粒子群算法主要是模仿鳥群捕食所設計的。通過觀察鳥群在捕食的時候發現某一塊區域出現食物，鳥群通過離食物最近的鳥發出信號過去捕食。所以在粒子群算法中，可以將鳥視作為粒子。粒子有各自被優化函數所決定的適應值，在空間內搜索最優函數解。粒子在搜索的過程中主要考慮的參數為速度以及位置變化。因為粒子位置的改變取決于其速度的大小：

式中：Vid（t）為粒子經過迭代計算后的速度；Pbest為粒子經過迭代計算在空間搜索范圍的最優位置；gbest為種群經過的迭代計算在空間搜索范圍上最優位置；c1為粒子的學習因子；c2為種群的學習因子；r1為粒子的隨機系數，取值（0，1）；r2為種群的隨機系數，取值（0，1）。

式中Xid（t）為粒子經過迭代計算后的位置。

2.3算法流程描述

為了保證機械臂末端執行器在使用的時候可以準確到達所設定的空間位置坐標，其根本為準確計算各個關節角的最優值。因此，本文將使用人工蜂群算法來計算出各個關節角的最優解，將計算所得最優解呈現的機械臂末端執行器的空間位置與設定的空間位置相比較，比較機械臂的位置誤差如下：

式中：ΔE為實際與設定之間的位置誤差；x1、y1、z1為人工蜂群算法所計算的機械臂執行器末端位置；x2、y2、z2為設定的機械臂執行器末端位置。

3仿真與分析

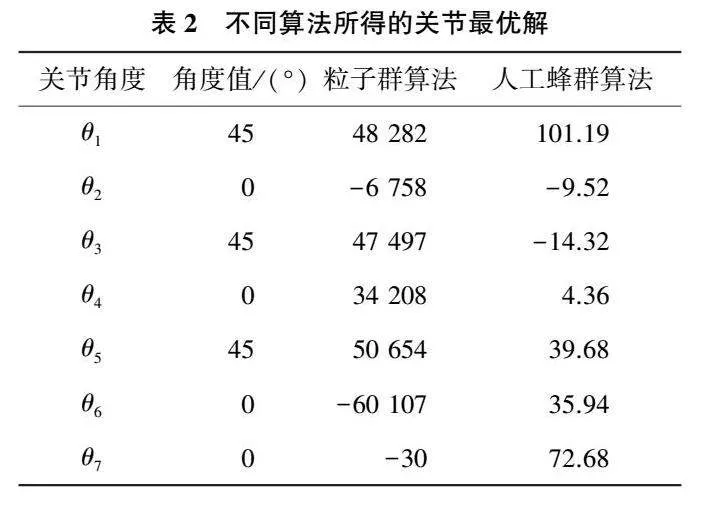
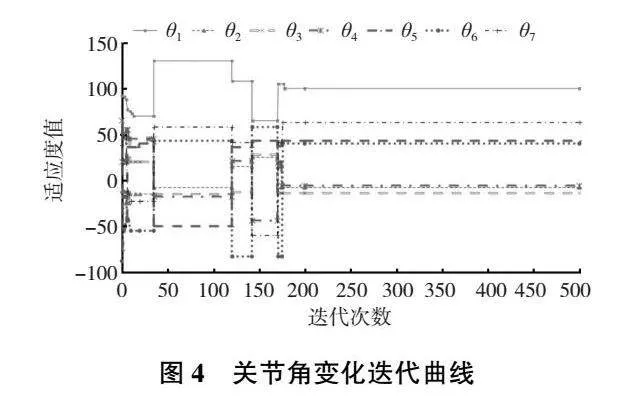
本文通過研究人工蜂群算法對7DOF機械臂進行逆運動學求解。在使用的時候可以通過手動調節改變機械臂的位置。手動調節后的機械臂位置所呈現的關節角度θ1—θ7依次為：45°、0°、45°、0°、45°、0°、0°。通過算法所得到的位置會和手動調節的有些許區別，本文將使用人工蜂群算法以最小位置誤差以及姿態誤差為目標讓機械臂運行到指定位置，將計算結果與粒子群算法進行比較，其中計算的最優解為（101.19，-9.52，-14.32，4.36，39.68，35.94，72.68），結果如表2所示，關節角變化迭代曲線如圖4所示。

圖4關節角變化迭代曲線

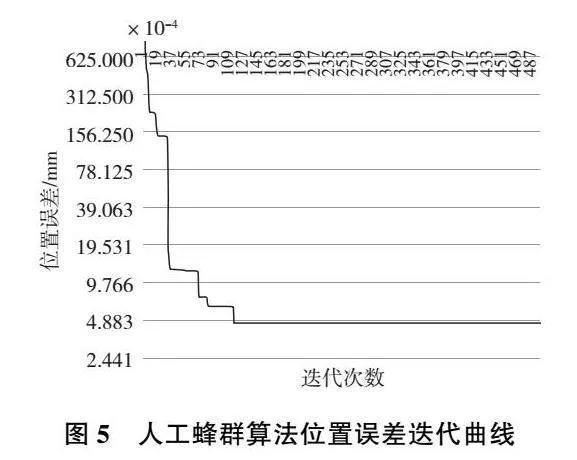
本次仿真實驗是在Matlab中編程來進行逆運動學的求解，主要研究的對象為7自由度冗余機械臂。其中設置的人工蜂群種群數為100，粒子群算法種群數為300，最大迭代次數為500。使用人工蜂群算法對機械臂逆運動學進行求解，運行該算法50次，其中設定的定位精度要求為：位置誤差不大于0.1mm，姿態誤差不大于10－3mm。當搜索精度達到該要求的時候，對應的關節角序列才滿足使用要求。其中隨著迭代次數的變化位置誤差的變化過程如圖5所示。

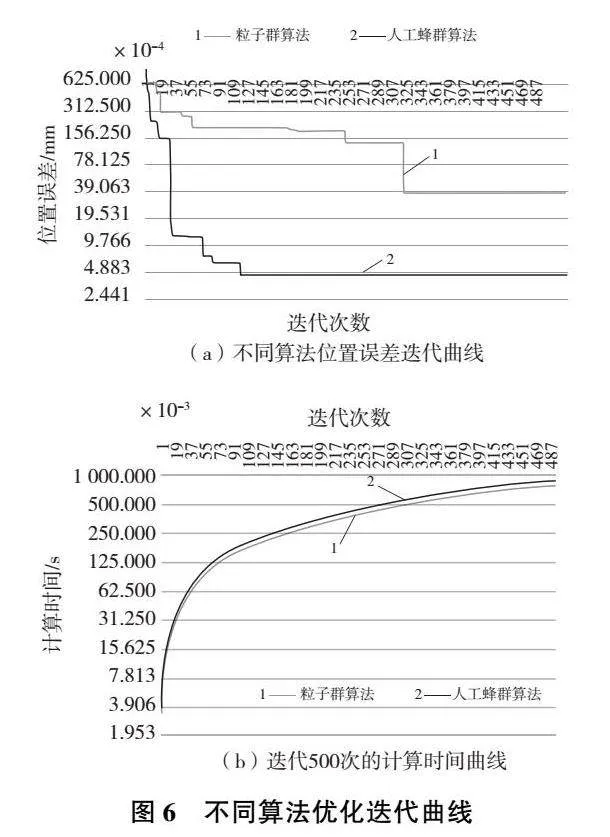
從圖5可以發現，人工蜂群算法經過多次迭代次數后，位置誤差會進行快速下降，最后趨于穩定的數據，位置誤差穩定在4.883×10－3mm。分別使用人工蜂群算法以及粒子群算法獨立運行50次，討論兩種算法之中位置誤差差距以及迭代500次所使用的計算時間均如圖6所示。

通過圖6（a）可以發現，人工蜂群算法在進行逆運動學求解中，隨著迭代次數的增加，收斂速度、位置誤差精度均優于粒子群算法。在迭代次數將近500次時，使用人工蜂群算法所對應的位置誤差穩定在10－4以下，而粒子群算法所對應的位置誤差穩定在10－3以下。通過圖6（b）可以發現人工蜂群算法與粒子群算法經過500次迭代次數所使用的計算時間較為接近，人工蜂群算法所使用計算時間略微少于粒子群算法。綜上所述可以得知，人工蜂群算法的搜索精度是優于粒子群算法的，收斂精度以及收斂速度是快于粒子群算法的。

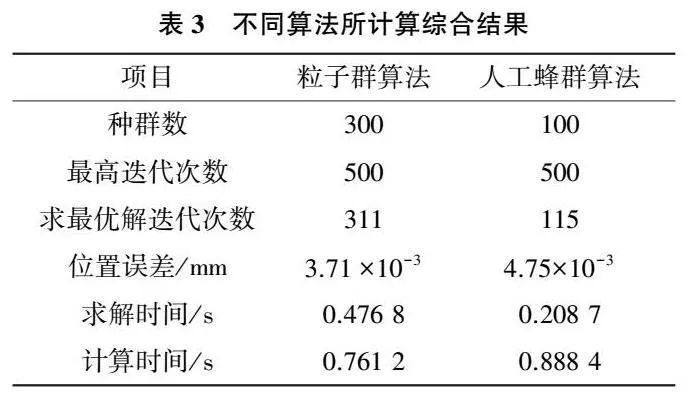
將上述人工蜂群算法以及粒子群算法所計算結果進行比較，如表3所示。

通過表3可以得知，粒子群算法所設置的種群數更多，有300個種群數，而人工蜂群算法的種群數才100個，種群數越多則搜多范圍更大，更有利于計算出最優解。但是通過求最優解的迭代次數可以得知，人工蜂群算法所使用的迭代次數更少，計算所得出的位置誤差也更小。另外對于兩種算法計算500次迭代的時間是相差不大的，但人工蜂群算法所使用的求最優解時間是少于粒子群算法的。

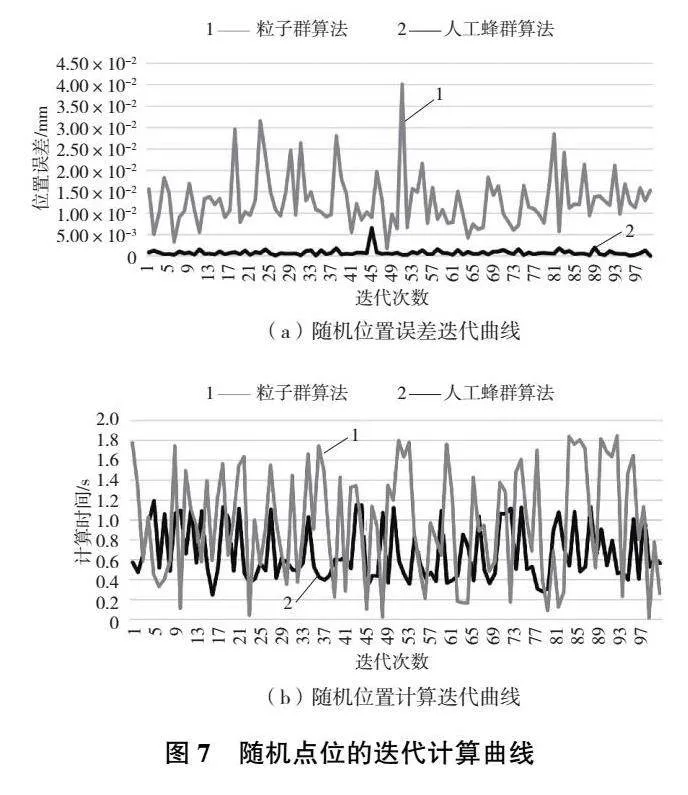
為了驗證兩種算法的實驗精確性，將在機械臂的工作空間隨機選擇100個位姿點進行逆運動學求解，其結果如圖7所示。

通過圖7（a）可以發現，對于冗余機械臂工作空間內隨機選取100個位姿點，人工蜂群算法收斂精度更好，粒子群算法收斂性比較不穩定，在兩種算法中人工蜂群算法的位置誤差精度更高；圖7（b）對于在不同點位計算最優解的過程，人工蜂群算法所使用的時間普遍比粒子群算法使用的時間少，收斂性更佳。

4結語

本文通過研究冗余機械臂的逆運動學求解問題，以探索最小的位置誤差以及姿態誤差為目標計算模型，提出使用人工蜂群算法的求解方法。通過仿真模擬分析后，可以得出以下結論：1）對于設定好的位姿點計算，采用人工蜂群算法計算所得的位置誤差、求解時間均優于粒子群算法，更適合實際應用；2）人工蜂群算法在求解過程中的收斂速度、收斂精度比粒子群算法優秀，求解的質量更高；3）在隨機多個位姿的逆運動學求解中，人工蜂群算法的位置誤差以及求解時間更加優秀，所展示的穩定性以及魯棒性優于粒子群算法。因此，通過仿真實驗證明，人工蜂群算法相對于粒子群算法更適用于移栽機械臂的使用，整體的位移精度更佳，后續會將本次編寫的人工蜂群算法添加至機械臂的控制器中，以便于更好地完成缽苗移栽工作。

參考文獻：

［1］ 徐文福，張金濤，閆磊，等. 偏置式冗余空間機械臂逆運動學求解的參數化方法［J］. 宇航學報，2015，36（1）：33-39.

［2］ 黨磊，熊瑞平，唐靜瑩，等. 同倫算法在6R機器人運動學逆解上的應用［J］. 機械，2017，44（4）：5-9.

［3］ 程浩田. 基于正逆運動學分析的機械臂時間最優軌跡規劃研究［D］. 太原：中北大學，2021.

［4］ 李娜托. 基于改進人工蜂群算法的冗余機器臂逆解研究［J］. 組合機床與自動化加工技術，2020（3）：37-40.

［5］ BAYATI M. Using cuckoo optimization algorithm and imperialist competitive algorithm to solve inverse kinematics problem for numerical control of robotic manipulators［J］. Proceedings of the Institution of Mechanical Engineers，Part I：Journal of Systems and Control Engineering，2015，229（5）：375-387.

［6］ 李憲華，孫青，張雷剛，等. 雙臂6R服務機器人的運動學研究及仿真［J］. 機械傳動，2018，42（5）：129-134.

［7］ 王騰，張承瑞，陳齊志，等. 利用增廣雅克比矩陣的冗余機械臂逆運動學求解算法［J］. 科學技術與工程，2021，21（16）：6752-6757.

［8］ 馬叢俊，趙濤，向國菲，等. 基于逆運動學的柔性機械臂末端定位控制［J］. 機械工程學報，2021，57（13）：163-171.

［9］ 魏延輝，韓寒，于園園，等. 構形平面方法求解冗余機械臂逆運動學［J］. 哈爾濱工程大學學報，2016，37（8）：1096-1102.

收稿日期：20230314

基金項目：浙江省尖兵領雁計劃項目（2022C02042）

第一作者簡介：王寒松（1997—），男，浙江臺州人，碩士研究生，研究方向為機械設計與開發，573415637@qq.com。

DOI：10.19344/j.cnki.issn1671-5276.2024.06.043