微元法在高中物理解題中的應用探討

【摘要】微元法作為高中物理中的重難點知識，在解題中有著廣泛應用.微元法可以將復雜的題目分割成若干簡單的小問題，幫助學生逐步攻克難題.本文通過典型例題，詳細說明微元法在高中物理解題中的應用，以供讀者參考.

【關鍵詞】微元法；高中物理；解題；應用

微元法通過對研究內容或過程進行無窮小的分割，將整體中的復雜部分簡化為單個簡明的片段，從而讓學生能夠從微觀角度洞察物理的變化，并最終理解整體的規律.該方法不僅促進了學生對物理知識的掌握，同時顯著增強了他們的問題解決能力.

1在運動學中的應用

例1根據圖像回答下列問題：

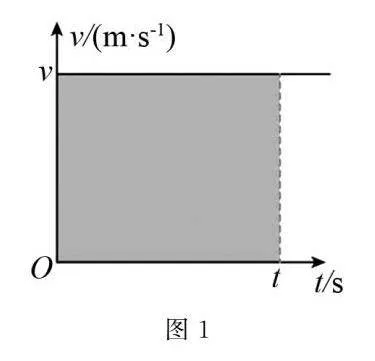
（1）以速度v做勻速直線運動的物體，時間t內的位移是什么？在圖1所示的圖像中可以用什么來表示？

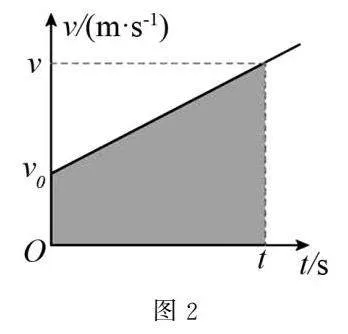
（2）圖2是勻變速直線運動的v-t圖像，根據（1）的結論，試猜想：勻變速直線運動的位移在圖2中可以用什么來表示？

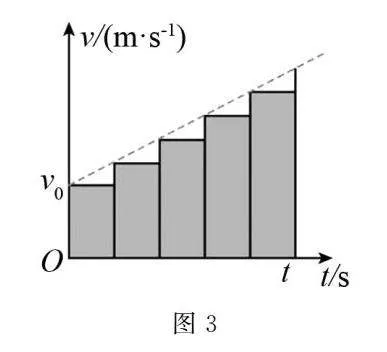
（3）如圖3，將圖2的運動分割成幾小段，因每段很短，可認為在這一小段上物體速度不變.基于此，在圖3中，各個小矩形面積的和表示的物理意義是什么？

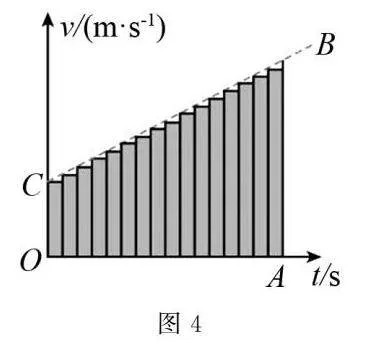
（4）如圖4所示，將圖2的運動劃分為更多的小段，對比圖4和圖3，分析（2）的猜想是否正確.

解析（1）物體以速度v做勻速直線運動，設位移為s，則時間t內的位移為s=v·t.在圖1的v-t圖像可知，橫坐標表示時間t，縱坐標表示速度v，由圖可知圖線圍成的面積表示位移.

（2）在圖1的v-t圖像可知，圖線圍成的面積表示位移.則可猜想：勻變速直線運動的位移在圖2中可以用面積來表示.

（3）若將圖2的運動分割成幾小段，因每段很短，可認為在這一小段上物體速度不變.因此，每小段上，速度與時間的乘積可近似為物體的位移.各小矩形的面積和近似為全過程中物體的位移.

（4）將運動過程劃為更多的小段后，把整個運動過程分割得很細，分割越細.這些小矩形的面積和便可更準確地反映物體的位移.所以（2）的猜想正確.

點評在本問題中，將物體的整個運動過程分割成若干個“微過程”，每個“微過程”可認為速度不變，速度與時間的乘積可近似為物體的位移.那么，各小矩形的面積和近似為全過程中物體的位移.巧妙地運用了微元法處理了這類運動問題.

2在靜電場中的應用

例2如圖5，圓心為O、半徑為R的均勻帶電圓環所帶電荷量為Q，P為垂直于圓環平面的對稱軸上的一點，OP=L，電場力常量為k，求P點處的場強大小.

解析如圖6所示，將圓環看成由n個小微元組成，當n足夠大時，每個小微元都可看作點電荷，其所帶電荷量Q′=Qn，則每個小微元在P點處產生的場強大小均為E=kQnr2=kQnR2+L2.由對稱性知，各個小微元在P點處的場強E沿垂直于對稱軸方向的分量Ey相互抵消，沿對稱軸方向的分量Ex之和即為帶電圓環在P點處的場強EP，所以EP=nEx=nkQnR2+L2cosθ=kQLR2+L232.

點評本題中，帶電圓環所帶的電荷量均勻分布，從圓環上任取一個微元，每個微元可看作點電荷，求出微元在P點的場強后，再運用場強的疊加求解圓環在P點的場強.

3在電磁感應中的應用

例3如圖7所示，兩平行金屬導軌水平放入磁感應強度為B、方向豎直向上的勻強磁場中，導軌間距為L，導軌左端接有一電容為C的平行板電容器.一質量為m的金屬棒ab垂直放在導軌上，在水平恒力F的作用下從靜止開始運動.棒與導軌接觸良好，不計金屬棒和導軌的電阻以及金屬棒和導軌間的摩擦.求金屬棒的加速度并分析金屬棒的運動性質.

解析運動過程分析：取一極短時間Δt，棒做加速運動，持續對電容器充電，則存在充電電流，

則F－BIL=ma，I=ΔQΔt，ΔQ=CΔU，ΔU=ΔE=BLΔv，

聯立可得F－CB2L2ΔvΔt=ma，

其中a=ΔvΔt，

則可得a=Fm+B2L2C，

加速度恒定，所以棒做勻加速直線運動.

點評在沒有明確加速度的變化情況之前，金屬棒的運動情況可能比較復雜，如果取運動過程中的極短時間Δt，可認為看認為在這一“過程微元”上電流不變，進而根據電學和力學相關知識進行求解.

4結語

綜上所述，微元法在高中物理解題中有著至關重要的地位.它為學生處理復雜物理問題提供了一種巧妙的思路，將不規則、連續變化的物理過程分割成無數個微小的單元，使問題簡化且更易理解.掌握微元法，不僅能提高學生解題的效率和準確率，更有助于培養他們的物理思維和科學探究能力.這要求教師在教學過程中重視微元法的講解和訓練，引導學生熟練運用微元法，讓學生在面對物理難題時能夠靈活使用這一有力工具，為高中物理學習和問題解決奠定堅實的基礎.

參考文獻：

[1]張家民.微元法在高中物理解題中的應用研究[J].中文科技期刊數據庫（引文版）教育科學，2023（3）：4.

[2]雷文勝.例談微元法在高中物理解題教學中的實踐應用[J].高中數理化，2023（S1）：107-108.