STEM理念下初中數學項目式學習活動設計

在現代教育中，綜合與實踐領域的學習越來越受到重視。《義務教育數學課程標準（2022年版）》明確指出，初中階段應主要采用項目式學習的方式，以問題解決為導向，讓學生在真實、多樣且具有挑戰性的情境中，綜合應用多學科知識，解決實際問題。然而，當前一些學校在實施STEM教育的過程中，對數學、物理、化學等領域的融合還不夠深入。在此背景下，費馬點問題作為一個經典的平面幾何優化問題，是一個理想的教學主題。它不僅在數學領域具有重要地位，也與日常生活中的選址問題緊密相關。教師以STEM理念采用項目式學習的模式教學，可以融合物理、數學等知識，引導學生探索解決集散點位置規劃的實際方法。學生將經歷完整的5E學習環教學過程，即認識問題、設計實驗并動手操作、原理解釋、模型精致和評價反思，能夠深入研究費馬點問題，構建起完整的知識體系。

學生參與這種跨學科的學習，不僅能夠提升數學素養，還能激發對科學和技術的興趣。下面，將結合案例闡述如何將這一理念應用于教學中。

一、5E學習環教學模式

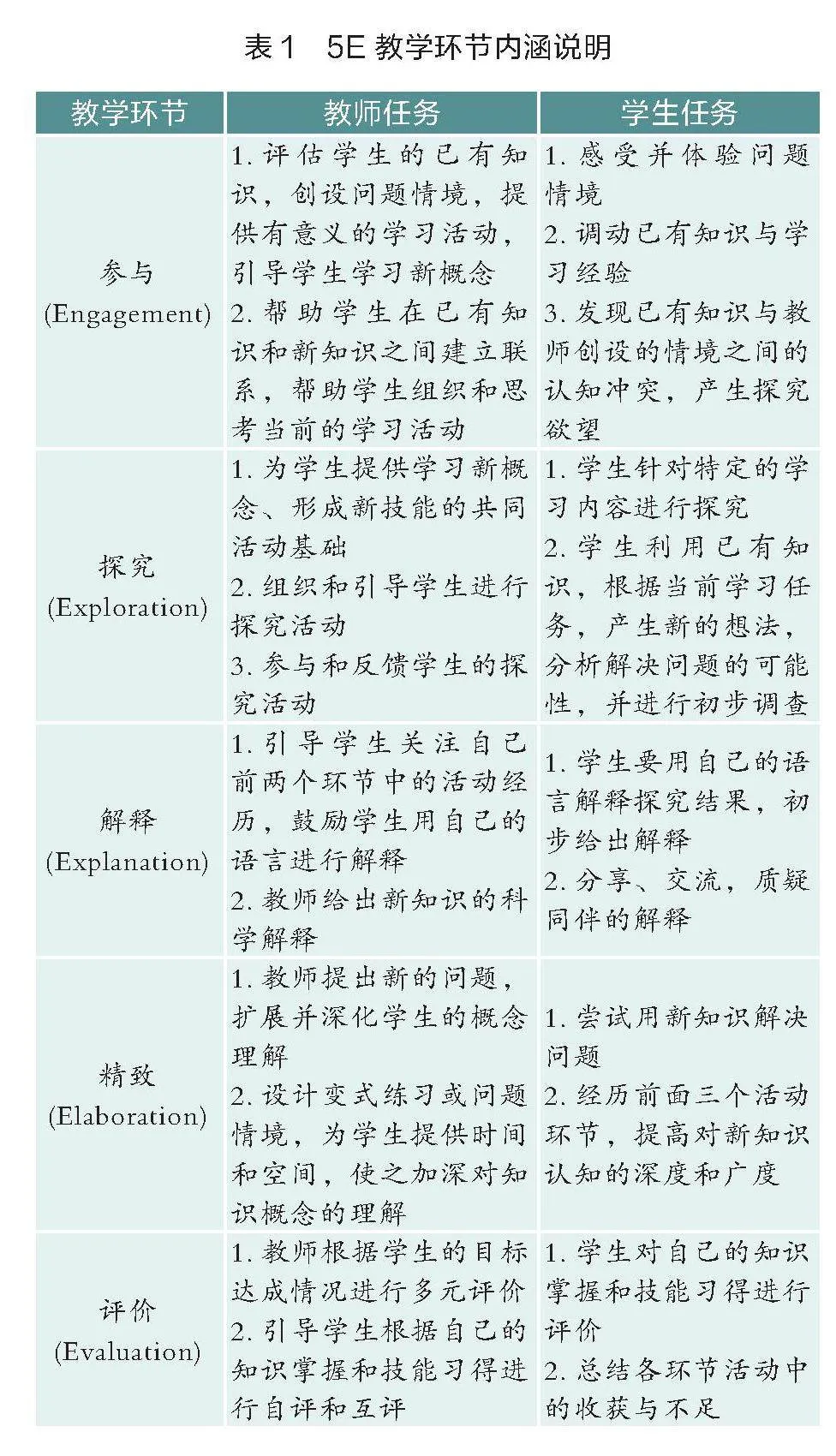
5E學習環是美國生物學課程研究會（BSCS）開發的一種建構主義教學模式，包括5個教學環節，即參與、探究、解釋、精致和評價。表1對這5個教學環節進行了說明，并闡述了每個環節教師和學生的主要任務[1]。

5E學習環是一種有效的具有實踐性、思維性、探究性的科學教育方法，其應用有助于增進學生對知識的理解。這一特征與STEM理念相契合。基于5E學習環設計STEM項目式學習，可以有效幫助學生構建概念，培養探究能力。

二、“規劃集散點位置”項目式學習活動的設計

費馬點問題是數學領域中平面幾何優化的經典議題。它與我們經常遇到的選擇最佳位置的優化問題息息相關。華羅庚先生曾將這一問題形象地比喻為“集散點問題”，其中所求的最優點即被稱為費馬點。在生活中，我們將集散點問題轉化為數學中的非線性規劃問題，采用微積分中求偏導數的方法，可以發現這一問題與力學中的力平衡有著緊密的聯系[2]。

教學對象為九年級學生。他們已經在八年級掌握了二力平衡的基本概念，且能夠尋找數學中基礎的最短路徑。此外，他們還學習了旋轉的相關知識，學有余力者可以在“將軍飲馬”問題的基礎上研究三條線段和最小的問題，增加學習的趣味性和挑戰性。為此，筆者設計一系列探究實驗，讓學生通過物理實驗和數學論證的雙重途徑，自行探索并找到最優點，從而更深刻地理解費馬點問題。如此實驗不僅能夠加深學生對費馬點的理解，還能激發他們對數學和物理的興趣，培養他們的實踐能力和創新思維。

（一）設計思路

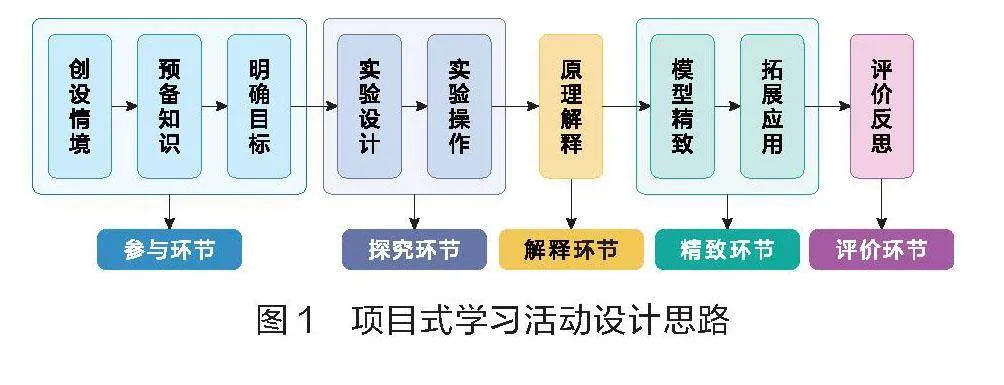
筆者根據5E學習環的各環節內涵，基于“規劃集散點位置”項目式學習活動設計了“五環節九步驟”教學流程（如圖1）。

在參與環節，筆者設計了與學生日常生活密切相關的問題，引導他們將這些問題與物理力學中的力平衡概念相聯系，從而在學生已有的二力平衡知識基礎上搭建橋梁。同時，利用微課幫助學生掌握力的合成法則，為后續實驗探究明確目標。在探究環節，學生設計并操作實驗，觀察實驗現象，記錄關鍵數據。在解釋環節，筆者讓學生運用物理和數學知識解釋實驗結果，嘗試構建費馬點問題的初步模型。進入精致環節，筆者設計一系列變式實驗，以幫助學生深化對費馬點問題的理解，完善他們對模型的認識，并應用新知識解決新問題。在評價環節，學生需要對自己的實驗操作和知識掌握情況進行自評和互評。同時，筆者對整個學習過程中表現出色的小組或學生給予積極評價，并針對存在的問題提出改進建議。

（二）設計環節

1.參與環節

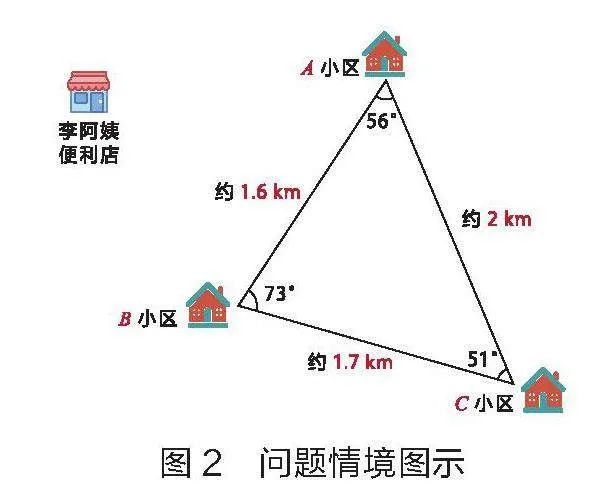
【創設情境】如圖2所示，李阿姨經營便利店，為了提升營業額，推出了“送貨上門”服務。經過觀察，她發現客源集中在A、B、C三個小區，且業務量大致相等。李阿姨計劃效仿物流公司的運營模式，設立一個“外送業務”的集散點，先將部分貨物存放于此，再分發到A、B、C三個小區。為降低運輸成本，她希望找到一個點，使得從該點到這三個小區的總距離最短。然而，如何找到這個集散點的最佳位置讓李阿姨感到困惑，于是她向正在大學攻讀物理專業的兒子求助。

李阿姨的兒子指出，這個問題實際上涉及物理中的三力平衡原理。那么，為什么這個問題會與三力平衡有關呢？這是因為在物理學中，尋找一個點使得它到三個固定點的距離之和最小，類似于在力學中尋找三個力的平衡點，使得合力為0。應用這一原理可以幫助李阿姨有效地解決集散點選址的問題。

【預備知識】關于力的平衡學生應該不陌生，他們已經學習過二力平衡，知曉作用在同一物體上的兩個力，如果大小相等、方向相反，并且在同一條直線上，這兩個力就彼此平衡。學生學習微課并思考：如果兩個力不在同一條直線上，那么對于物體的作用效果是怎樣的呢？如何理解上述問題中的“三力平衡”呢？為什么要尋找到三個小區的距離之和最短的集散點位置，這與物理學中力的平衡的知識有什么關系嗎？

原理解讀：根據物理彈性力學中的平衡態公理（又稱最小勢能原理）可知，當一個質點受到幾個始終分別指向某個定點的力時，若物體處于穩定平衡狀態，即質點所受合力為0，則該體系處于勢能最小狀態。進一步可以推出這樣的結論 ：質點處于穩定平衡狀態時，該質點到幾個定點的單程距離或多程距離之和最小[3]。

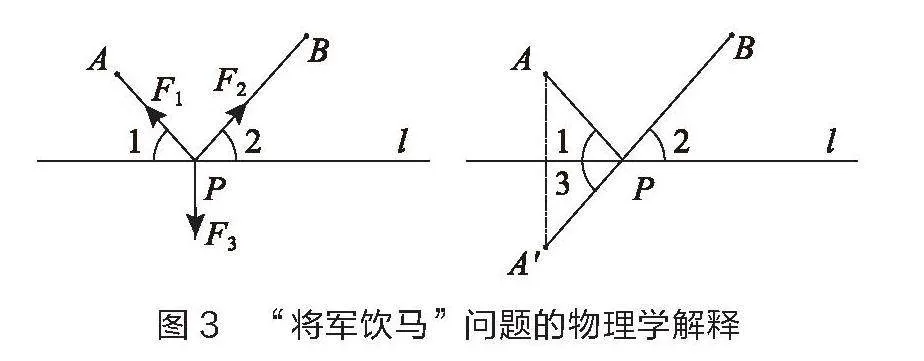
原理應用：大家熟悉的最短路徑問題“將軍飲馬”就可以用物理學的知識來解釋。如圖3所示，A、B為直線l同側的兩個定點，點P為直線l上的一個動點，當AP+BP最小時點P的位置在哪？此時，將動點P視為一個質點，它分別受到指向A、B的兩個力F1和F2。由原理可知，當點P處于穩定平衡狀態，即點P所受三個力的合力為0時，AP+BP的值最小。此時，F1和F2在直線l方向的分力相等，因此當AP、BP與直線l所成的夾角相等，即∠1=∠2時， AP+BP最小。這與我們解決“將軍飲馬”問題的幾何解法是一致的，作點A關于直線l的對稱點A'，連接A'B，與直線l的交點P即為所求。易知∠1=∠3，∠2 =∠3，即∠1=∠2。

設計意圖：借助微課清晰講解力的合成遵循的“平行四邊形法則”和三力平衡相關知識。基于二力平衡的物理實驗，探索“將軍飲馬”問題中的動點位置，以此作為預備知識傳授給學生。這樣不僅能夠培養學生提取和應用信息的能力，還能為后續的實驗設計和操作打下堅實的基礎。

【明確目標】關鍵任務是從微課中獲取靈感，設計實驗，幫李阿姨找到集散點的位置，即滿足這個位置到三個小區的總距離最短這一條件。

2.探究環節

有了參與環節的鋪墊，學生已經明確了探究問題，掌握了基礎知識。此時筆者以問題驅動的方式引導學生設計實驗。

預設問題：三個小區的相對位置對集散點的選取是否有影響？如何體現三個小區的位置？如何體現“A、B、C三個小區業務量大致相等”？

學生首先思考問題，分組合作，討論設計物理實驗的操作步驟，然后闡述小組選擇的實驗方式及理由，預測實驗結果等，最后在全班范圍內討論，選擇一個最優化的實驗步驟。

實驗器材：木板、手動打孔器、小圓環、細線、50 g砝碼（三個）、量角器等。

實驗分五步進行。第一步：將地圖中的問題抽象出一個△ABC，從地圖中測量出AB、AC、BC的長度及內角的角度，根據三條線段長度比例關系，確定三個小區的相對位置。第二步：選擇一塊木板，將△ABC畫在木板上，在三個頂點處鉆孔并打磨光滑。第三步：選擇長度適中的三根細繩，將一端穿過小洞，另一端系在木板上方的一個小圓環上。第四步：將三個質量相等的砝碼分別掛在三根細繩上，先使細繩保持不受力狀態，再將三個砝碼同時松手，小圓環靜止時就是三力平衡的狀態。第五步：在三力平衡的情況下，采用測量線段長度、角的度數等方式觀察小圓環的位置有什么特點。

3.解釋環節

學生完成操作后發現，小圓環停在△ABC內部，如將小圓環抽象成點P，會發現∠APB、∠APC和∠BPC的大小均約等于120°（如圖4）。筆者引導學生分組交流，思考為什么在三力平衡狀態下，這三個角都近似為120°，進而思考這個點P是否能滿足PA+PB+PC最小這一條件。

本環節筆者給學生充足的思考時間，適時予以點撥，幫助學生運用物理和數學知識，從角度和長度等視角分析點P。

從物理的角度看（如圖5），F1=F2，根據力的合成法則（平行四邊形法則），可知合力F方向必與菱形對角線重合。處于平衡狀態時，第三個力F3與合力F等值、反向。根據菱形的性質，易證這三個力間形成的張角都是120°。

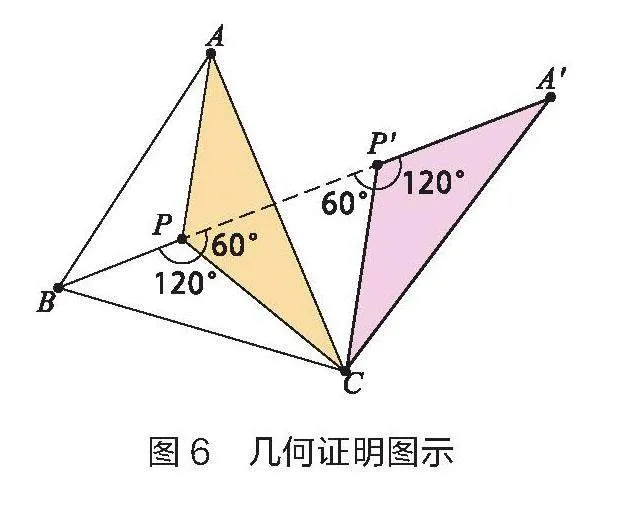
從數學的角度看，學生已經掌握驗證距離之和最短的基本方法，就是經過一系列的圖形變化將幾條線段轉化到同一條直線上。此時恰好是線段和最短的時候。如圖6所示，將△APC繞點C順時針旋轉60°，△PCP'為等邊三角形，可知∠PP'C=∠P'PC=60°，根據前面實驗得到∠BPC=120°，易證BP、PP'、A'P'共線。根據旋轉的性質可知，PA+PB+PC=A'P'+P'P+PB=A'B。為更加形象地說明共線時是線段之和最小的時候，筆者再任選一點P，根據兩點之間線段最短的原理加以說明。

學生從不同視角審視分析后對集散點的位置有了清晰的認識，有助于確定點P的位置。此時，學生很容易想到數學中的“定位神器”——點的坐標。學生通過分組討論，班內分享，明確了確定點的位置的基本方案，即借助兩次旋轉變換后形成的直線求出交點坐標。

此時，筆者借助數學軟件GeoGebra快速求解，確定點P的位置，并引導學生利用方位角的知識準確表達集散點位置。將實際問題中三個小區的相對位置按 1∶20000縮小后，以點B為原點建立坐標系，構建△ABC，利用軟件計算可得到點P的坐標，也可以采用方位角進行表述：李阿姨大約應在B小區北偏東69°，距離B小區0.76 km的位置設置集散點。

4.精致環節

通過前面幾個環節的探究與解釋，學生基本掌握尋找集散點的方法和原理。筆者提出一個新問題，讓學生思考。

情境拓展：李阿姨根據大家設計的解決方案設立了集散點P，取得了很好的銷售業績，準備進一步拓展業務。如圖7所示，李阿姨這次打算針對X、Y、Z三個小區也開設一個集散點。能否按照前面的實驗操作幫助李阿姨解決問題？

設計意圖：在前面幾個環節中，師生共同探究出了三個內角均小于120°的費馬點的情況。精致環節中，主要是讓學生對于費馬點問題進一步加深認識。為節省時間，筆者演示物理實驗。此時，小圓環停止在X小區的位置，與前面的探究結果產生矛盾。以此引導學生關注這一問題中出現的大于120°的內角，讓學生嘗試從物理學和數學視角解釋問題。

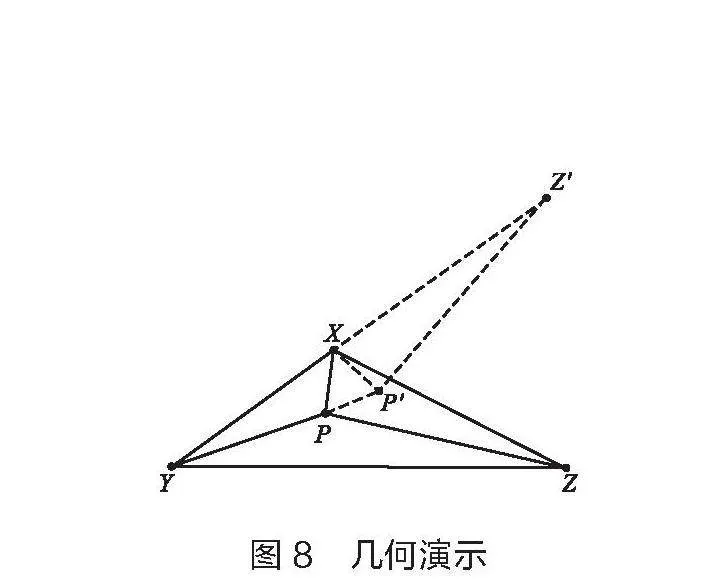
解決問題：與前面的實驗一樣，由于F1= F2，且力的合成遵循平行四邊形法則，故合力F必然在菱形的對角線方向上。但由于兩個力的張角大于120°，可知合力F要小于第三個力F3。因此，小圓環會落在X小區的位置。從數學角度也可證明。如圖8所示，將△XPZ繞點X逆時針旋轉，使得XZ'與XY共線，由于∠YXZ＞120°，可知∠ZXZ' ＜60°，即旋轉角小于60 °，所以∠PXP' ＜60°，所以PX＞PP'，PX +PY+PZ＞PP'+PY+P'Z'＞YZ'= XY+XZ'，也就是說當點P和點X重合時，距離之和最小。

此時學生發現，將集散點設置在X小區內，距離之和最短。在師生共同解決這一問題后，筆者給出費馬點的定義：費馬點是指位于三角形內且到三角形三個頂點距離之和最短的點。學生回顧整個實驗操作過程總結得出結論：若三角形三個內角均小于120°，那么費馬點在三角形內部 ；若三角形有一個內角大于等于120°，則費馬點在鈍角頂點處。此時，學生對于三角形中的費馬點問題的認知結構得到進一步完善。

5.評價環節

筆者引導學生回憶實驗操作過程，以及原理解釋過程，總結收獲，反思不足。引導學生從學習解決問題的思想方法的角度進行總結。例如：在三力平衡的學習上是類比遷移了二力平衡的知識；探尋費馬點的數學原理解釋的過程應用到了數學抽象，運用旋轉變換轉化線段；模型精致階段大于120°問題的提出，體現了分類討論的思想等。更重要的是培養了學生的綜合能力，即學會分析情境中的各種信息，并用科學合理的方式加以抽象，從而更好地解決問題。

三、教學實施建議

（一）整合信息技術，提高課堂教學效率

STEM課程以其跨學科的特性，強調學生、學科以及社會之間的緊密聯系。在現實生活中，許多實際問題并非理想化，若僅依靠人工處理，不僅耗時，還可能掩蓋問題研究的本質。根據認知負荷理論，人在學習過程中能夠處理的信息量是有限的。因此，教師應利用信息技術直觀展示知識，并輔助學生處理復雜的計算問題，可以提高課堂效率。例如，在項目式學習中，將力的合成和三力平衡的概念以微課形式呈現，既通俗易懂又便于學生應用；在解釋環節確定點P的位置時，利用GeoGebra軟件可以直接獲得坐標，有效減輕學生的認知負擔，提高效率。

（二）精心設計STEM課程，實現“手腦”協同發展

筆者開展STEM課程教學，將技術、工程學科與科學、數學教育置于同等重要的位置，強調了過程與實踐的重要性。在設計STEM課程時，教師應重視學生的動手實踐環節，確保活動既具有思考性又具備可操作性，讓學生在數學和科學的理論知識指導下，完成實驗操作和模型制作等活動。以三力平衡模擬實驗為例，教師需引導學生將實際問題抽象成數學模型，并在“實踐”與“思考”的互動中，實現“手腦”的協同發展。

（三）促進學科交叉融合，完善學生知識體系

STEM課程的豐富性不僅體現在多學科的交叉融合中，近年來“STEM”還向“STEAM”拓展，引入了人文藝術教育。這表明學科之間并非孤立存在，而是相互聯系。數學作為基礎學科，雖然具有理論性和抽象性，卻是許多學科研究的基礎。一種有效的方法是從現有的數學教學資源出發，尋找與其他學科的聯系，設計項目式學習活動。教師將數學的理論性與物理的實踐性相結合，可以讓學生對知識有更深刻的理解，從而完善學生的知識體系，充分發揮STEM教育的價值。

參考文獻

[1] 王健，李秀菊.5E教學模式的內涵及其對我國理科教育的啟示[J].生物學通報，2012（3）：39-42.

[2] 張蓮蓮，黃忠裕，俞勝濤.幾類特殊的費馬點問題及其初等解法[J].中國科教創新導刊，2011（22）：87.

[3] 鄧清.基于平衡態公理的一類最短路徑問題探究[J].中國數學教育，2022（8）：56-59.

（作者胡璽舜系天津師范大學濱海附屬學校教師；佘文娟系天津師范大學濱海附屬學校高級教師）

責任編輯：祝元志