趣味數獨：數對法

當一單元中某兩格僅可能為兩個數字時，稱這兩格構成數對。如果格A和格B是數對，那么它們的值僅可能是a和b（a和b是1～9之間的任何兩個數字），可以將該數對記為{a，b}。

數對出現在宮里，成為宮數對；出現在行（列）中，稱為行（列）數對。

根據抽屜原理，格A和格B構成數對{a，b}，格A和格B的值只能是a和b，而不可能是其他數。這就是數對有別于普通區塊的重要性質，即數對的占位作用。

大部分的數對是排除的結果，通過排除法形成的數對稱為排除數對；還有一部分數對是通過余數法形成的，通過余數法形成的數對稱為余數數對。

下面請嘗試找出下列例題的數對。

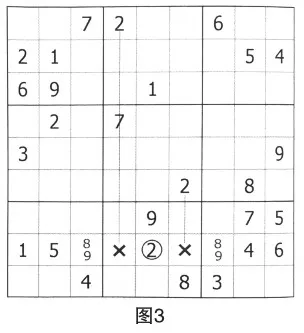
1.數對R（2，3）C3={6，8}是排除數對，是由數字6和8對第一宮排除形成的。第一宮中，空格R1C1、R1C3及R2C1排除數字6和8，因此數字6和8只能在空格R2C3和R3C3中。

2.數對R（8，9）C7={5，6}是排除數對，是由數字5和6對第九宮排除形成的。

3.數對R（8，9）C2={4，6}是余數數對。第二列中只有這兩個空格，也就是說除了4和6，其他數字在第二列中已經全部出現。

4.數對R5C（4，6）={6，9}是余數數對，空格R5C4和R5C6的余數只有數字6和9。

觀察下列例題，找出第八宮中空格R8C5中的數字。

注意觀察第八宮，已經出現了數字8和9，故空格R8C4和R8C6中的數字排除8和9。

因此，對于第八行，存在數對R8C（3，7）={8，9}。

考慮數對R8C（3，7）的占位作用，用數字2對第八行進行排除，R8C5=2。

數對的應用主要是數對排除法、數對替代法以及數對占位法。

下面例題中，如果能發現數對，得到唯一解就比較容易了。

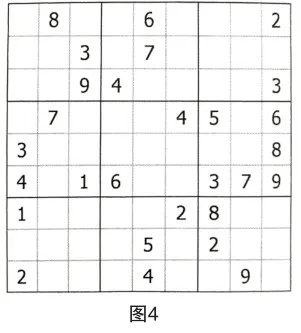
如下圖所示，第一宮中，應用宮排除法，發現數對R（2，3）C2={1，2}。

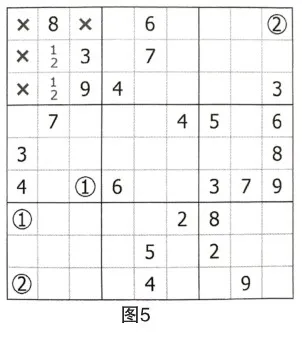
第一步：第一宮R（2，3）C2={1，2}，應用數對占位法，R1C3=4。

數對的占位作用在這里至關重要。因為用數字4對第一宮進行排除，空格R2C2和R3C2是不能確定是否排除數字4，而數對R（2，3）C2的存在，使這兩個空格排除了1和2以外的數字。

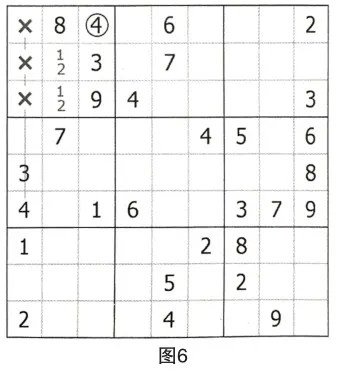
第二步：由于R（2，3）C2={1，2}，因此應用數對替代法，R6C2=5。

如果不考慮數對的作用，空格R6C2的余數就是2和5；如果考慮數對，利用其替代作用，空格R6C2的余數就僅剩下數字5。

如下圖所示，用數字1對第九列進行排除，發現區塊R（8，9）C9=1。

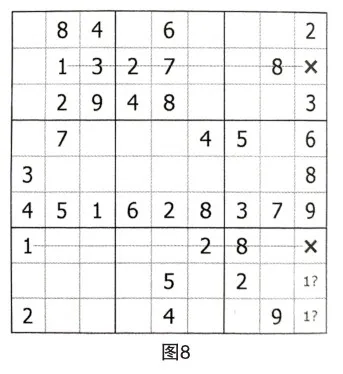
如下圖所示，用數字7對第三宮進行排除，發現區塊R（1，3）C7=7。

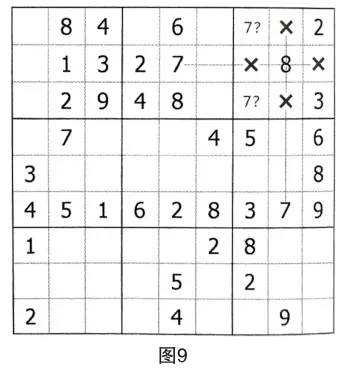
第三步：應用區塊替代法，考慮到區塊R（8，9）C9和R（1，3）C7的替代作用，點算空格R9C7的余數，得到R9C7=6。

進展至此，下一步的突破口應該選擇哪里？

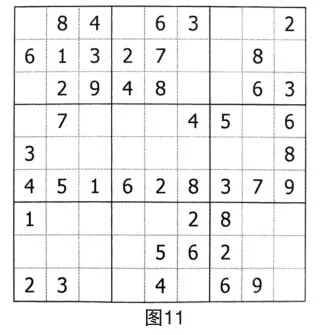
用數字5和7對第五宮進行排除，發現數對R5C（4，6）={5，7}。

第四步：用數字9對第六列進行排除，因為數對R5C（4，6）={5，7}對空格R5C6的占位作用，得到R2C6=9。

至此，后續的工作均可以通過基礎算法完成，不再贅述。

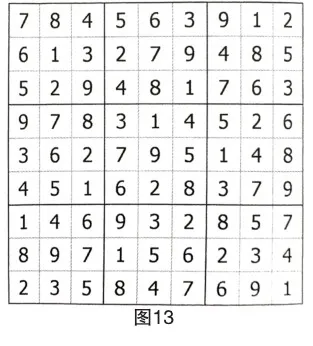
下面試著挑戰一下后面的習題吧！

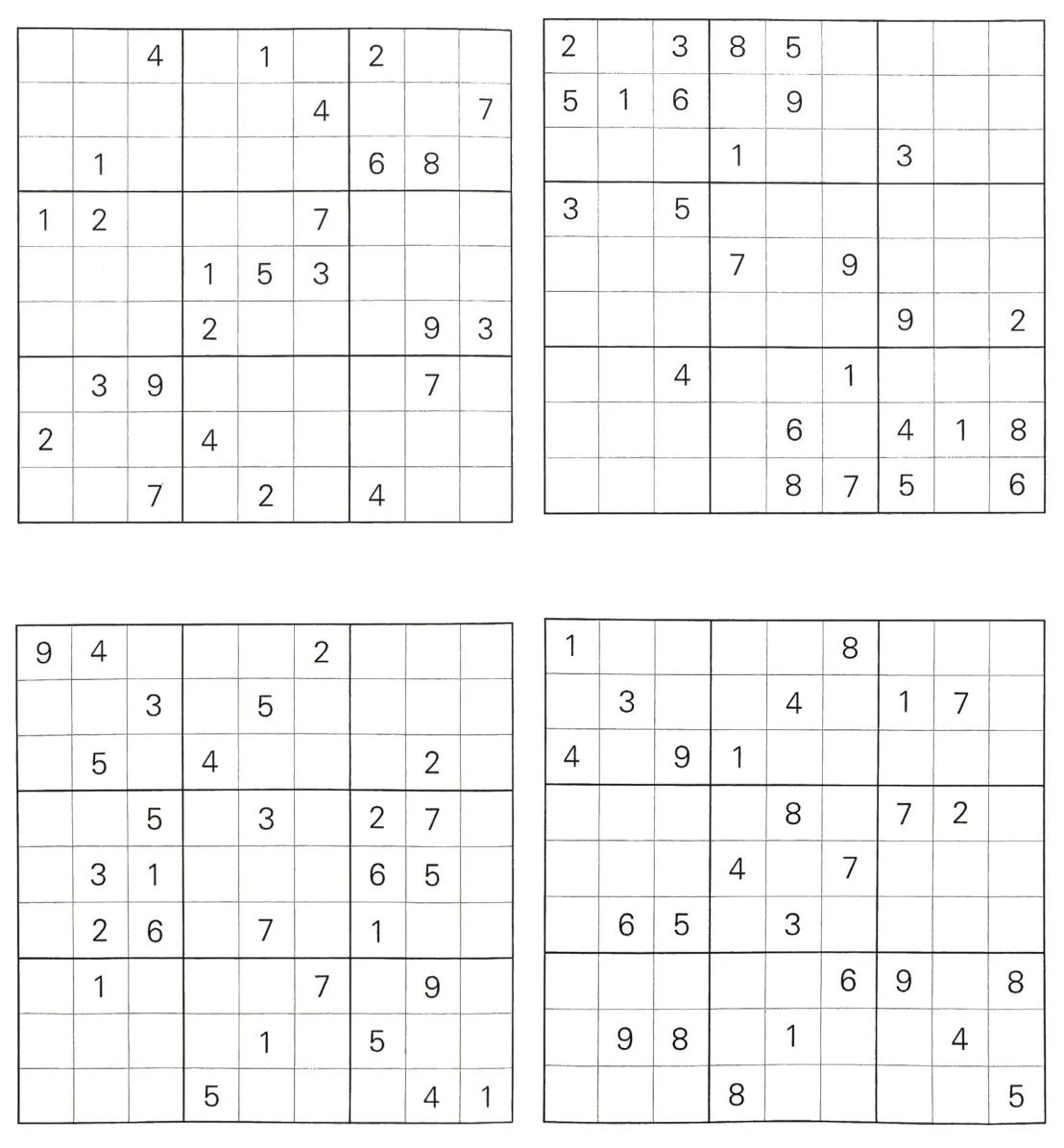
（摘自化學工業出版社《數獨游戲：從基礎到精通，讓你越玩越聰明》）