基于生存期的碼頭構件維修維護決策模型

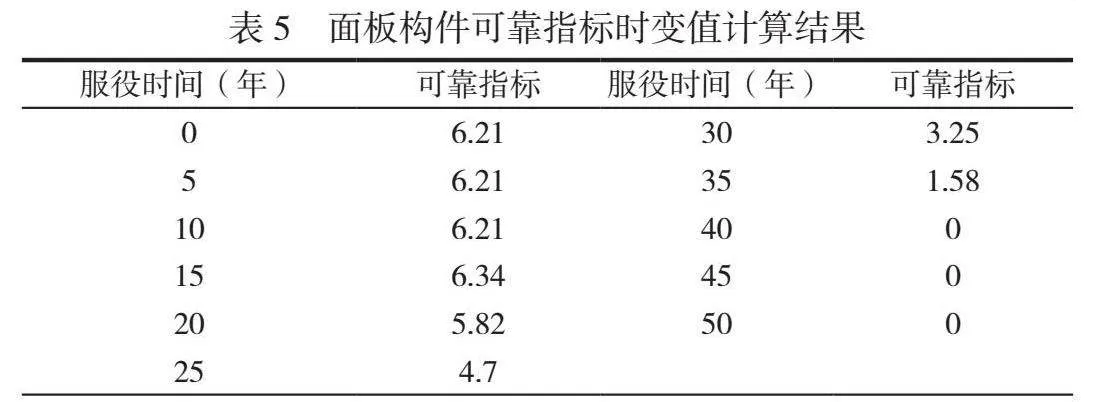
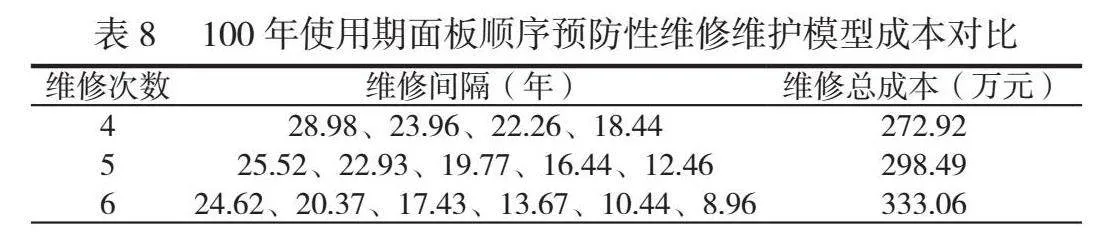
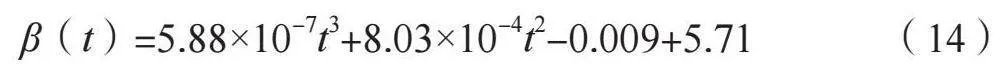
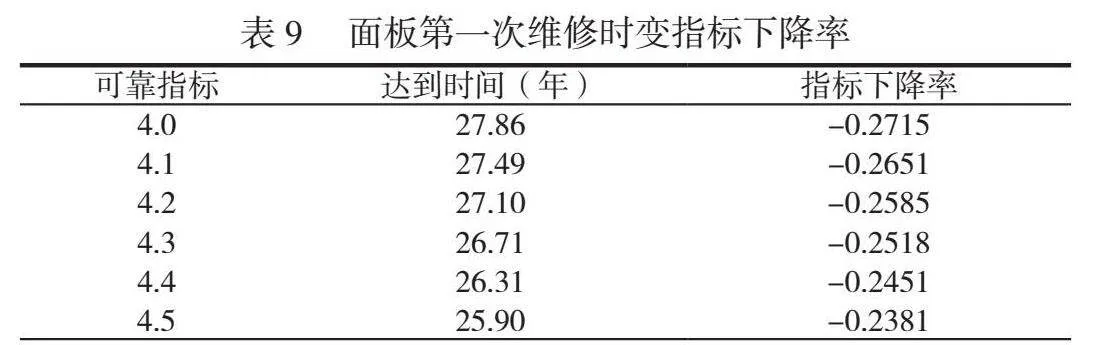
摘 要：為了確定高樁碼頭結構構件最優維修計劃，本文應用結構時變可靠度理論對構件進行可靠性評估，并引入役齡回退因子對維修過程進行模擬。綜合考慮可用度因素、風險性因素以及經濟性因素，基于生存期概念建立了高樁碼頭結構構件維修維護決策模型，綜合分析不同維修策略的特點對決策模型進行細化，使維修計劃具有預見性、及時性，并通過算例驗證了模型的有效性。

關鍵詞：時變可靠度理論；役齡回退因子；維修維護決策模型；生存期

中圖分類號：TU 39" " " " " 文獻標志碼：A

在港口的運營過程中，工程結構的損傷是不可避免的，因此為高樁碼頭結構構件提供一種具有預見性、及時性的維修決策方法，建立相應的維修維護決策模型，具有重要的工程價值。目前處于主流地位的有兩種方法。

1 以可靠性為基礎的維修決策

該方法英文全稱“Reliability Centered Maintenance”，簡稱RCM維修決策理論[1]。

在高樁碼頭維修決策領域，國內外對RCM理論的研究與應用取得了一定進展，本文在此基礎上進行接續研究。

2 基于全生命周期的維修決策

基于全生命周期的維修決策方法，是指綜合考慮結構從建設到拆除的整個生命周期內的維修總成本對結構進行維修決策的方法。

本文結合全生命周期的維修決策方法，利用時變可靠的理論，引入役齡回退因子對碼頭構件的維修效用進行模擬，基于碼頭構件的生存期建立維修維護決策模型，為工程決策人員提供一種合理安排碼頭構件的維修計劃的方法。……