基于DECWOA的配電網(wǎng)故障定位技術(shù)要點(diǎn)探究

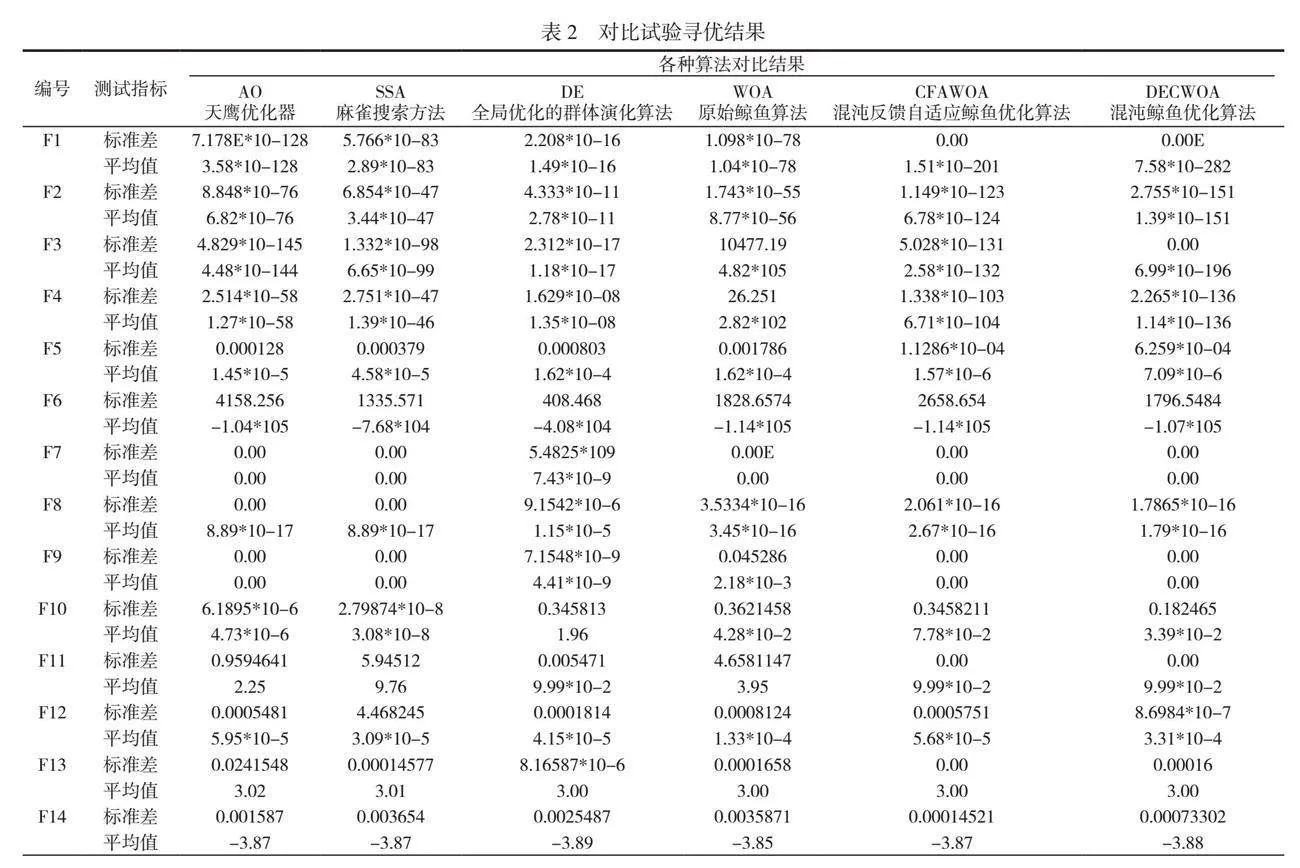
摘 要：本研究的主要目的是提高配電網(wǎng)故障定位技術(shù)的精確性，針對(duì)鯨魚(yú)優(yōu)化算法存在的局部尋優(yōu)與全局優(yōu)化不平衡問(wèn)題，通過(guò)引入差分進(jìn)化算法，提出了混沌鯨魚(yú)優(yōu)化算法（DECWOA）。試驗(yàn)表明，與傳統(tǒng)鯨魚(yú)優(yōu)化算法相比，DECWOA在配電網(wǎng)故障定位中的定位精確度更高。該研究為提高配電網(wǎng)故障定位的準(zhǔn)確性和效率提供了一種新的方法，為故障定位問(wèn)題提供了更可靠的解決方案，這一研究成果對(duì)電力系統(tǒng)的穩(wěn)定運(yùn)行具有積極的推動(dòng)作用。

關(guān)鍵詞：DECWOA；配電網(wǎng)故障定位；Sine映射

中圖分類(lèi)號(hào)：TM 73 " " " " 文獻(xiàn)標(biāo)志碼：A

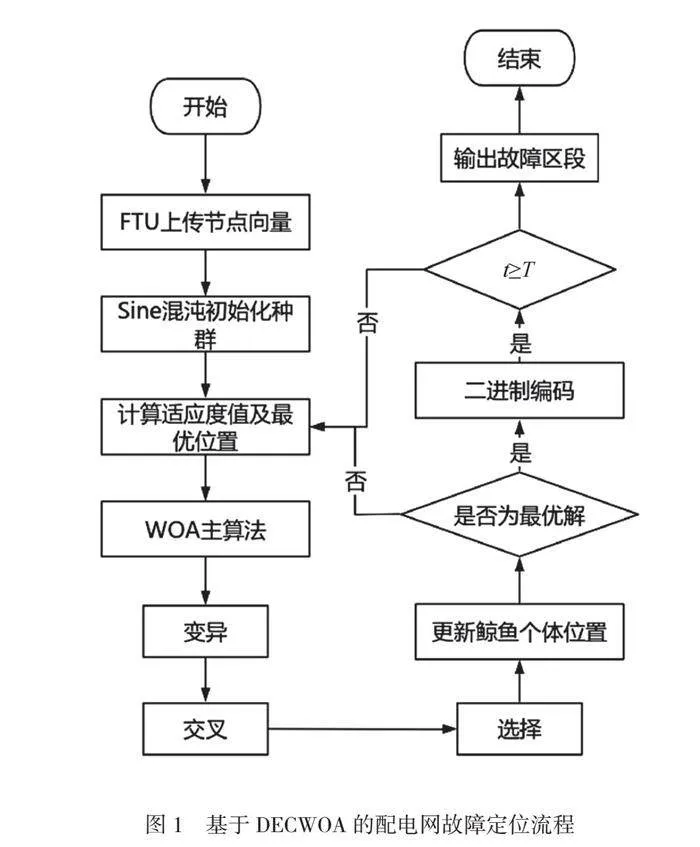
當(dāng)面對(duì)復(fù)雜多變的電力系統(tǒng)時(shí)，傳統(tǒng)的故障定位方法存在一定的局限性，例如難以有效地對(duì)多節(jié)點(diǎn)同時(shí)發(fā)生信息畸變的情況進(jìn)行處理。為了解決這個(gè)問(wèn)題，本研究聚焦引入改進(jìn)的鯨魚(yú)優(yōu)化算法（DECWOA）來(lái)優(yōu)化配電網(wǎng)故障定位技術(shù)。DECWOA基于原始的鯨魚(yú)優(yōu)化算法（WOA）并通過(guò)3種有效的改進(jìn)策略提高了其在尋優(yōu)過(guò)程中的性能，尤其是防止陷入局部最優(yōu)狀態(tài)的問(wèn)題。本研究旨在深入探究DECWOA在配電網(wǎng)故障定位中的應(yīng)用要點(diǎn)，對(duì)其性能和有效性進(jìn)行分析和試驗(yàn)驗(yàn)證。

1 鯨魚(yú)優(yōu)化算法的改進(jìn)策略

1.1 Sine映射初始化種群

在本次研究中，相關(guān)研究人員嘗試對(duì)鯨魚(yú)優(yōu)化算法進(jìn)行改進(jìn)，通過(guò)引入混沌映射來(lái)提高算法的精度和收斂速度。在具體實(shí)踐中，研究人員考慮了2種混沌映射方式，即Logistic映射以及Sine映射，試驗(yàn)發(fā)現(xiàn)，Logistic混沌映射導(dǎo)致初始化種群主要集中在區(qū)域的右上部分和邊界處，Sine混沌映射導(dǎo)致初始化種群分布相對(duì)均勻[1]。……