裝配式建筑套筒灌漿飽滿度和密實度檢測方法研究

摘 要：目前裝配式建筑的技術(shù)難點是利用套筒灌漿連接構(gòu)件。因此本文針對套筒灌漿密實度進行無損檢測，基于阻尼振動的方法，提出了一種基于密實度指數(shù)的灌漿質(zhì)量評價方法。在阻尼振動檢測方法中，振動波形通過套筒灌漿會出現(xiàn)衰減，不同介質(zhì)的衰減程度不同，由此可以檢測灌漿質(zhì)量問題。由于所在區(qū)間的不同，因此密實度指數(shù)可以準(zhǔn)確地評價套筒灌漿的密實度，若大于0.5，則表現(xiàn)均勻密實。在測試試驗中，本文采用14點位綜合測量的方法，對5個工程的灌漿套筒進行檢測，證實了本文所提出的檢測方法和評價方法的有效性。

關(guān)鍵詞：裝配式建筑；套筒；灌漿；飽滿度；密實度

中圖分類號：TU 75" 文獻(xiàn)標(biāo)志碼：A

在城鎮(zhèn)化建設(shè)的過程中，民用住宅需求持續(xù)增加，這為建筑行業(yè)提供了一個非常好的發(fā)展契機。在這樣的情況下，各種新的技術(shù)開始涌現(xiàn)，更具實用性和穩(wěn)定性的方法逐漸成熟，并獲得廣泛應(yīng)用[1]。在民用住宅施工的過程中，裝配式建筑結(jié)構(gòu)已經(jīng)成為一種很常用的方式。這種方法不僅施工質(zhì)量好，而且施工效率也比較高，可以在保證質(zhì)量的前提下加快施工進度。在裝配式建筑施工的過程中，套筒灌漿技術(shù)是影響建筑質(zhì)量的最重要因素之一[2]。在裝配式建筑的構(gòu)件連接處，一般以套筒為連接件，內(nèi)部為鋼筋，在套筒和鋼筋之間灌入高強度砂漿，從而對構(gòu)件間進行連接。在這種處理方式下，裝配式建筑連接處的強度取決于套筒和高強度砂漿之間的連接強度、高強度砂漿和鋼筋之間的連接強度[3]。由此可見，如果套筒內(nèi)高強度砂漿灌注飽滿并且密實，就可以獲得更好的連接強度，從而保障裝配式建筑整體的安全性。因此，在這種情況下，對套筒灌漿后的飽滿度和密實度進行檢測，就成為判定灌漿質(zhì)量是否達(dá)標(biāo)的重要依據(jù)。本文主要采用不破壞建筑外觀的無損檢測方法進行研究工作。

1 基于阻尼振動的無損檢測方法

在裝配式建筑的構(gòu)件連接過程中，套筒灌漿后，內(nèi)部質(zhì)量形成一個隱蔽的工程。因為套筒為金屬、灌漿為非金屬、鋼筋為金屬，所以灌漿后就形成了多層的金屬和非金屬交錯的一種結(jié)構(gòu)形態(tài)。而從實際施工經(jīng)驗來看，套筒內(nèi)砂漿的厚度并不大，受內(nèi)部鋼筋所占體積制約，砂漿層厚度僅為5mm～6mm。

比較薄的砂漿層一旦出現(xiàn)灌注不均的情況，就會大大降低套筒連接的強度，導(dǎo)致極大的安全隱患。如果采用鉆孔法進行灌漿質(zhì)量檢測，就會破壞建筑結(jié)構(gòu)。因此，建立套筒灌漿質(zhì)量無損檢測方法勢在必行。

本文采用基于阻尼振動的方法對灌漿飽滿度和密實度進行檢測，以明確套筒內(nèi)的灌漿質(zhì)量優(yōu)劣。振動波形產(chǎn)生后，在介質(zhì)傳播過程中，會逐漸衰減和削弱。但是，不同介質(zhì)對振動波形的衰減能力是不同的。如果灌漿足夠飽滿和密實，那么振動波形主要受到砂漿介質(zhì)的衰減作用影響。如果灌漿不夠飽滿和密實，就會有空氣夾雜于其中，振動波形會同時受到砂漿和空氣或者是只受到空氣介質(zhì)的衰減影響。

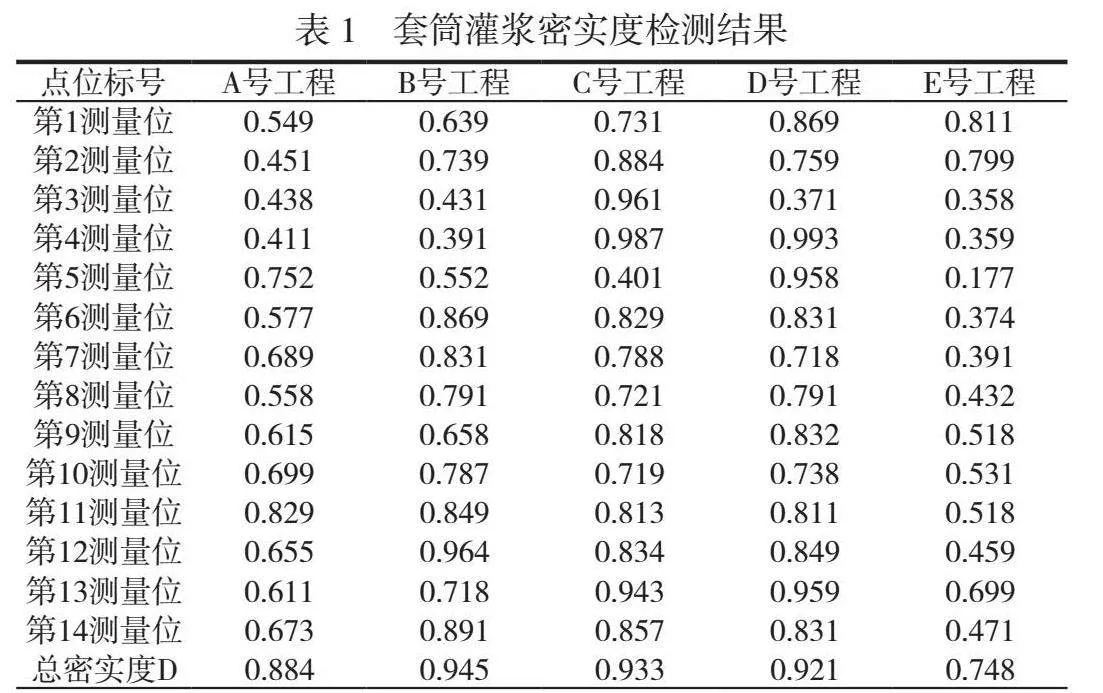
阻尼振動是指振動波形在介質(zhì)傳輸?shù)倪^程中，會受到介質(zhì)所帶來的阻尼效應(yīng)而逐漸衰減。在衰減的過程中，振動波形的幅度會逐漸變小。介質(zhì)給振動波形施加的摩擦阻力的計算過程如公式（1）所示。

fr=-γv " " " " " " " " " " " " " " " "（1）

式中：fr為振動波形在介質(zhì)中傳播時受到的摩擦阻力；γ為介質(zhì)施加給振動波形的阻力系數(shù)；v為振動波形在某一種介質(zhì)中傳播的速度。

根據(jù)牛頓第二定律，可以將振動波形傳遞的過程描述為一個二階常值系數(shù)方程，計算過程如公式（2）所示。

（2）

式中：x為振動波形的幅度，也稱位移參量；t為振動波形傳遞的時間；β為介質(zhì)的阻尼系數(shù)，因介質(zhì)不同而不同；ω0為振動波形的固有角頻率。

阻尼系數(shù)的計算方法如公式（3）所示。

（3）

式中：β為介質(zhì)的阻尼系數(shù)；γ為介質(zhì)施加給振動波形的阻力系數(shù)；m為介質(zhì)質(zhì)量。

固有角頻率的計算方法如公式（4）所示。

（4）

式中：ω0為振動波形的固有角頻率；k為介質(zhì)給振動波形提供的彈性模量；m為介質(zhì)質(zhì)量。

振動波形及其在介質(zhì)中的衰減狀態(tài)，如圖1所示。

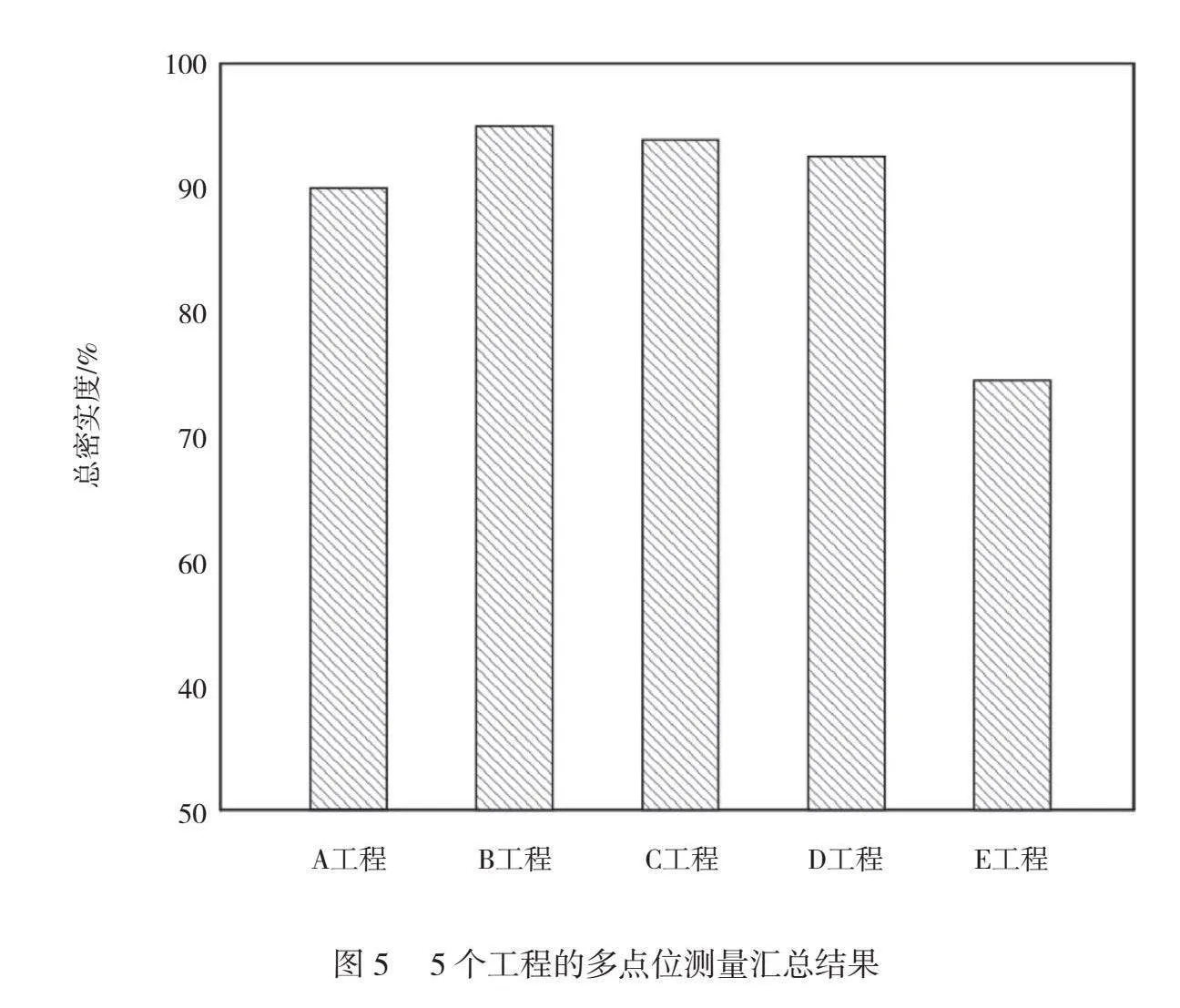
套筒、砂漿、鋼筋形成連接形態(tài)后，如圖2所示。

圖2中，振動波形通過套筒灌漿連接件后，就會逐步衰減，通過這個衰減程度就可以判斷內(nèi)部砂漿的介質(zhì)均勻性。

2 灌漿飽滿度和密實度的質(zhì)量評價

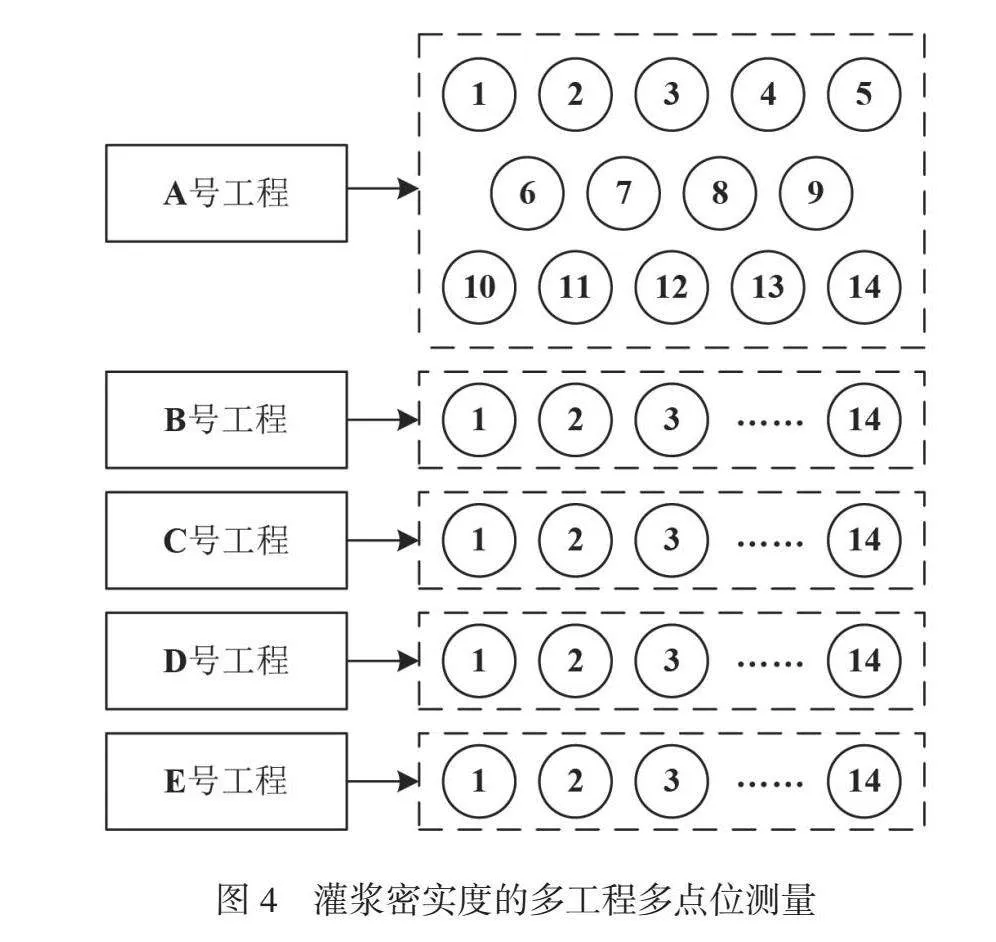
利用阻尼振動法對套筒灌漿質(zhì)量進行檢測，要根據(jù)特定的評價參數(shù)來判斷灌漿質(zhì)量。這時，可能會出現(xiàn)灌漿密實、不密實和沒有灌漿等情況，如圖3所示。

對套筒內(nèi)灌漿的飽滿度和密實度來說，領(lǐng)域內(nèi)有最具針對性的密實度指數(shù)，其數(shù)學(xué)表達(dá)如公式（5）所示。

β=1-Sv-Sp " " " " " " " " " " " " " " " （5）

式中：β為灌漿密實度；Sv為振動波形被板底反射后速度受到的影響；Sp為振動波形被界面反射后速度受到的影響。

灌漿密實度指數(shù)表示了密實度的程度。當(dāng)灌漿密實度指數(shù)大于0.5，小于1.0時，表明灌漿密實。當(dāng)灌漿密實度指數(shù)位于大于0，小于0.5時，表明灌漿不密實，這時可能存在小規(guī)模的空洞甚至是半空。當(dāng)灌漿密實度指數(shù)小于0時，表明灌漿有大規(guī)模的空洞甚至是全空。

速度受到的影響的計算過程如公式（6）所示。

（6）

式中：Vsd為灌漿密實區(qū)域?qū)τ谡駝硬ㄐ蔚姆瓷洳ㄋ伲籚r為測試點位對于振動波形的反射波速；ηv為兩種反射波速的比值。

在實際工作狀態(tài)下，Vr受到的影響是多方面的，不僅是灌注的砂漿，鋼筋混凝土的材質(zhì)、套筒的壁厚、鋼筋的埋藏深度、振動波形的波長、灌注砂漿可能存在的缺陷，也都會對Vr產(chǎn)生影響。因此，僅利用Vr進行判斷可能不夠準(zhǔn)確。可以利用Si反映套筒的厚度對測速點間距等變化的影響，如公式（7）所示。

（7）

式中：Vi為在第i個測量點位測得的振動波形波速，Vi+1為在第i+1個測量點位測得的振動波形波速，?s為第i個測量點位和第i+1個測量點位之間的距離，H為第i個測量點位和第i+1個測量點位之間的間板厚度。

3 裝配式建筑套筒灌漿密實度檢測試驗

利用基于阻尼振動的污損檢測方法和灌漿質(zhì)量評價方法對裝配式建筑套筒灌漿的密實度進行檢測。

本文采用的是多工程多測量點位的檢測方法。選擇5個裝配式建筑工程，分別是A號工程、B號工程、C號工程、D號工程、E號工程，在每個工程中選擇了14個測量點位，如圖4所示。

按照本文提出的灌漿密實度指數(shù)，可以對套筒灌漿飽滿度和密實度進行質(zhì)量評價，因為本文布置了多個測量點，所以此處再構(gòu)建一個多測量點位平均密實度指數(shù)，結(jié)果如公式（8）所示。

（8）

式中：D為多測量點位平均密實度指數(shù)；N為灌漿密實度測量的點位總數(shù)；Bi為第i個測量點位上得到的灌漿密實度指數(shù)。

為了方便量化評價結(jié)果，因此給Bi一個更清晰的賦值，具體操作方法如公式（9）所示。

（9）

式中：當(dāng)βi大于0.5小于1.0時，表明灌漿密實；當(dāng)βi大于0小于0.5時，說明灌漿不密實，這時可能有小規(guī)模空洞甚至是半空情況；當(dāng)βi小于0時，說明灌漿有大規(guī)模的空洞甚至是全空。

按照上述方法，對圖4中5個工程的套筒灌漿密實度進行檢測，得到的結(jié)果見表1。

在表1中，第一列表示14個測量點位和各點位匯總后的總密實度，第二列為A號工程、第三列標(biāo)為B號工程、第四列為C號工程、第五列為D號工程、第六列為E號工程。

5個工程的多點位測量匯總結(jié)果，如圖5所示。

從匯總結(jié)果可以看出，B號工程14個點位的套筒的灌漿密實度最好，為0.945。其次是C號工程14個點位的套筒灌漿密實度，為0.933。排在第三位的是D號工程14個點位的套筒密實度，為0.921。第四位的是A號工程14個點位的套筒灌漿密實度，為0.884。灌漿密實度最差的是E號工程14個點位的套筒密實度，為0.748。根據(jù)這一組測量結(jié)果可以看出：本次灌漿的總體質(zhì)量很好，只有E號工程應(yīng)該采取進一步的處理措施以提高其密實度質(zhì)量。

4 結(jié)論

裝配式建筑已經(jīng)成為我國城市民用建筑的重要形式，該建筑極大地提高了城市建設(shè)的施工質(zhì)量和施工效率。在裝配式建筑的實踐過程中，完成裝配件連接是最關(guān)鍵的工藝。套筒連接是最常見的裝配式連接方式。因為套筒為金屬、灌漿為非金屬、鋼筋為金屬，所以灌漿后就形成了多層金屬和非金屬交錯的一種結(jié)構(gòu)形態(tài)。為了檢驗套筒連接后內(nèi)部灌漿的密實度，本文構(gòu)建了阻尼振動模型。利用這種模型可以準(zhǔn)確分析套筒內(nèi)灌漿的密實程度。結(jié)果表明，對不同位置的套筒連接進行密實度檢驗，阻尼振動模型都能有效地檢測密實度。

參考文獻(xiàn)

[1] 陳旭東，汪秀娟，劉志豪，等. 無損檢測技術(shù)在套筒灌漿密實度檢測中的應(yīng)用研究[J]. 蘭州工業(yè)學(xué)院學(xué)報，2017，24（1）：49-53.

[2] 李寧波，錢稼茹，葉列平，等. 豎向鋼筋套筒擠壓連接的預(yù)制鋼筋混凝土剪力墻抗震性能試驗研究[J]. 建筑結(jié)構(gòu)學(xué)報，2016，37（1）： 31-40.

[3] 李麗紅，耿博慧，齊寶庫，等. 裝配式建筑工程與現(xiàn)澆建筑工程成本對比與實證研究[J]. 建筑經(jīng)濟，2022，35（9）：102-105.