趣味數獨：區塊替代法

通過對基礎算法的介紹我們已經知道，某格的同位群中如果出現了8個不同的數字，該格的值就是唯一沒有出現的那個數字。

有些時候，雖然不能明確某個數字的具體位置，但如果可以確認這個數字必然出現在區塊中，而這個區塊恰好又屬于目標空格的同位群，那么這個區塊就完全可以參與到余數點算過程中，這就是區塊替代法。

區塊替代法是余數唯一法的進階應用。

圖1這個標準數獨題，從目前的局面看似乎有點兒無法下手。該如何破局呢？

如圖2所示，第四宮，應用宮排除法，發現區塊R（5，6）C3=3；

然后，用數字3對第一行進行排除，發現區塊R1C（8，9）=3；

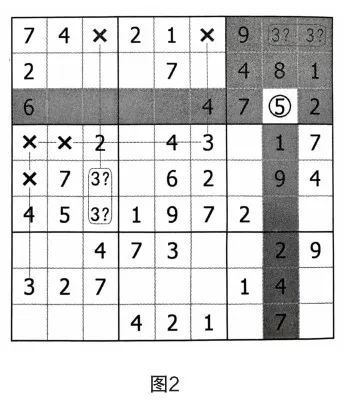
第1步：區塊替代法，R1C（8，9）=3，點算空格R3C8的余數，可以得到余數唯一解R3C8=5。

在這里，排除法形成的區塊R1C（8，9）替代了數字3。

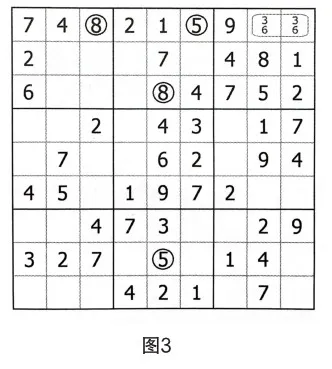
第2步：余數唯一法，R3C5=8。

第3步：第五列，應用單元唯一法，R8C5=5。

第4步：應用區塊替代法、余數唯一法，R1C6=5。

區塊R1C（8，9）=3，并且R1C（8，9）=6，應用區塊替代法，點算空格R1C5的余數，根據余數唯一法得出解。

第5步：區塊替代法，R1C3=8。

至此，后續均可以通過基礎解法得出答案，不再贅述。

如此看來，善于發現并運用區塊替代法，解題將勢如破竹。

下面試著挑戰一下后面的習題吧！