基于壓縮感知的智能反射面信道估計

摘" 要：

針對智能反射面（intelligent reflecting surface， IRS）輔助的通信系統中稀疏度未知信道的估計問題，提出了一種基于壓縮感知的稀疏自適應信道估計算法。首先，研究了正交匹配追蹤（orthogonal matching pursuit， OMP）算法下信道的殘差l2范數與輸入的信道稀疏度之間的關系，得出了OMP算法恢復稀疏度未知信道的迭代終止條件;然后，提出了一種二階段稀疏自適應信道估計算法，在第一階段估計信道稀疏度，在第二階段增加或刪減支撐集原子，最終使得恢復的信道向量誤差最小。仿真結果表明，與經典的最小二乘法、已知稀疏度的OMP算法、稀疏自適應匹配追蹤（sparsity adaptive matching pursuit， SAMP）算法相比，提出的算法性能良好，魯棒性強。

關鍵詞：

智能反射面; 壓縮感知; 稀疏自適應; 信道估計

中圖分類號：

TN 929.5

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.07.31

Channel estimation on intelligent reflecting surface based on compressed sensing

LIU Gang， LI Yuhang， YANG Qingxin， GUO Yi*

（School of Telecommunications Engineering， Xidian University， Xi’an 710071， China）

Abstract：

A sparse adaptive channel estimation algorithm based on compressed sensing is presented to estimate sparse unknown channels in intelligent reflecting surface （IRS） assisted communication systems. First， the relationship between the l2 norm of the channel residual under the orthogonal matching pursuit （OMP） algorithm and the sparsity of the channel is studied， and the iteration termination conditions for the OMP to restore the sparsity of unknown channels are obtained. Then， a two-stage sparse adaptive channel estimation algorithm is presented. In the first stage， the channel sparseness is estimated， and in the second stage， the supporting set atoms are added or deleted to minimize the channel vector errors recovered. The simulation results show that the performance and robustness of the proposed algorithm are better than those of classical least squares， OMP with known sparsity， and sparse adaptive matching pursuit （SAMP）.

Keywords：

intelligent reflecting surface （IRS）; compressed sensing; sparse adaptability; channel estimation

0" 引" 言

智能反射面（intelligent reflective surface， IRS）以其低成本、能夠有效提升通信系統性能而備受關注［13］。IRS包含大量被動反射元件，每個元件都能引起入射信號的相位移動并進行反射［3］。通過自適應調整IRS的相移矩陣，可以提高接收信號的功率，從而提高傳輸質量［4］。此外，IRS是被動地反射信號，無需額外能耗［5］。

由于上述優良特性，研究人員已經對IRS輔助的各種無線系統的設計和性能進行了廣泛的研究，例如IRS輔助的正交頻分復用（orthogonal frequency division multiplexing， OFDM）系統［610］、IRS輔助的多輸入多輸出（multiple input multiple output， MIMO）通信［1113］、IRS輔助的非正交多址（non-orthogonal multiple access， NOMA）［1417］等。值得注意的是，IRS需要準確的信道狀態信息（channel state information， CSI）來調整反射系數，從而實現對無線傳播環境的高度控制，因此信道估計是IRS輔助通信系統中的關鍵技術之一。然而，由于缺少用于基帶信號處理的有源部件，低成本無源IRS元件只能反射信號，不能像傳統無線通信系統中的有源收發機那樣通過處理導頻信號來進行信道估計。此外，IRS通常由大量無源元件組成，這些無源元件通常在IRS相關信道中具有大量信道系數，導致IRS信道估計的訓練開銷顯著增加。因此，不同于傳統的移動通信系統中的信道估計［18］，包含IRS的通信系統CSI的獲取極具挑戰性［19］。

對于工作在毫米波和太赫茲頻段的IRS輔助通信系統，由于嚴重的路徑損耗和偶爾的阻塞，IRS與基站（base station， BS）以及用戶終端（user equipment， UE）之間只存在有限數量的散射路徑。因此，IRS相關信道通常在角度域中表現出強稀疏性。而壓縮感知技術通過利用信道的稀疏性，以很低的訓練開銷來恢復稀疏信號，逐漸成為IRS信道估計中的一個有前景的工具。對于具有稀疏信道的IRS輔助通信系統，級聯信道估計可以轉換為稀疏信號恢復問題［20］并通過現有的壓縮傳感方法有效解決［2124］。文獻［25］表明，由于公共IRS-BS信道的稀疏性，所有UE的級聯信道矩陣共享公共行列塊稀疏結構。因此，其提出了基于壓縮感知的信道估計方案，以低訓練開銷聯合恢復所有UE的級聯CSI。文獻［26］利用了毫米波信道在角域和延遲域中的雙重稀疏性，提出了基于壓縮感知的寬帶信道估計，并進一步減少了訓練開銷。另一方面，通過利用信道中的稀疏性，已經開發了用于IRS信道估計的各種壓縮感知算法。其中，正交匹配追蹤（orthogonal matching pursuit， OMP）算法是一種低復雜度算法，已經在許多文獻中被討論。文獻［2729］改進了OMP算法，以解決角域中的級聯信道估計問題。然而，文獻［2729］均假設信道稀疏度為已知，盡管IRS大多部署在固定位置，但是BS和UE在信道估計之前無法獲取信道稀疏度。因此，針對未知稀疏度的信道，本文提出了一種針對IRS輔助的MIMO通信系統的稀疏自適應信道估計算法。

本文首先將IRS輔助的MIMO系統信道估計問題抽象為稀疏信號恢復問題，并根據OMP算法輸入稀疏度和輸出結果的殘差向量l2范數之間的關系，得出了恢復未知稀疏度信道的迭代終止條件：相鄰兩次迭代輸出殘差向量對應的l2范數應當小于某一門限值。隨后提出了一種稀疏自適應信道估計（sparsity adaptive channel estimation，SACE）算法，將信道估計分為兩個階段，在第一階段估計稀疏度，并儲存當前所估計的稀疏度對應的支撐集，

在第二階段對該支撐集進行修改，最終獲取精確的信道估計結果。最后以歸一化均方誤差（normalized mean squared error，NMSE）為標準給出了仿真結果。仿真結果表明，對于未知稀疏度的信道，本文提出的算法性能優于稀疏自適應匹配追蹤（sparsity adaptive matching pursuit， SAMP）算法，并且可達到與已知稀疏度的OMP算法相近的性能。

1" 系統模型

1.1" 系統模型

圖1給出了IRS輔助的單UE MIMO系統模型。圖中，BS配備數量為M的均勻線陣列（uniform linear array，UPA）天線，IRS配備數量為N的UPA反射元件，UE配備1根天線。需要特別指出，這里不考慮BS和UE之間的直接鏈路，因為直接鏈路信道估計問題可以通過關閉所有IRS上的反射元件，直接采用傳統信道估計方案來解決［11］。

經過IRS反射的級聯信道F（t）可以表示為

F（t）=GV（t）h∈CM×1（1）

式中：G∈CM×N表示IRS到BS的信道矩陣;h∈CN×1表示從UE到IRS的信道矩陣;V（t）=diag（v（t））∈CN×N表示一個由v（t）組成的對角矩陣，v（t）是IRS上的反射系數向量，可以表示為

v（t）=［β1，tejθ1，t，β2，tejθ2，t，…，βN，tejθN，t］∈CN×1（2）

式中：βn，t∈［0，1］和ejθn，t∈［0，2π］分別表示在第n個反射元件上t時刻的反射幅度和反射相位配置。

具體地，G和h可以重寫為

G=NMNf∑Nfp=1αpaM（AoAp，θAoAp）aHN（AoDp，θAoDp）（3）

h=NNh∑Nhq=1βqaN（AoAq，θAoAq）（4）

式中：Nf和Nh分別表示BS-IRS信道G的路徑數以及IRS-UE信道h的路徑數;αp和βq分別表示G中第p徑的復增益以及h中第q徑的復增益;AoAp和θAoAp分別表示BS側的到達方位角（azimuth angle of arrival，AAoA）以及到達仰角（elevation angle of arrival，EAoA）［30］;AoDp和θAoDp分別表示從IRS側的出發方位角（azimuth angle of departure，AAoD）以及出發仰角（elevation angle of departure，EAoD）;同理，AoAq和θAoAq分別表示從UE到IRS的AAoA和EAoA;aN和aM分別表示IRS的陣列導向向量和BS的陣列導向向量，由下式定義：

aL=1L1，ej2πλd［（2－1）sin sin θ+（2－1）cos θ］，…，

ej2πλd［（L－1）sin sin θ+（L－1）cos θ］T（5）

式中：L表示UPA總天線數目;d為天線之間的距離;λ為無線電波長。

BS接收到的信號可表示為

y（t）=GV（t）hx（t）+w（t）=Gdiag（h）v（t）x（t）+w（t）=Hv（t）x（t）+w（t）（6）

式中：x（t）表示傳輸的導頻符號;w（t）表示服從CN（0，σ2I）復高斯分布的加性噪聲，σ2為噪聲功率，I為單位矩陣;H=Gdiag（h）為等效信道。因此，反射級聯信道的估計問題轉變為已知導頻符號和IRS上的相移向量v（t），根據接收到的觀測向量y（t）來估計等效信道H的問題。

1.2" 信號模型

由于毫米波通信中存在嚴重的路徑損耗和阻塞效應，發射機和接收機之間只存在少數多徑分量［12］。因此，毫米波信道在角域表現出稀疏性，因此可以使用基于壓縮感知的信道估計方法。等效信道H可以在虛擬角域（virtual angular domain， VAD）使用過完備字典矩陣來表示［31］，即

H=DMHaDHN（7）

式中：DM∈CM×Gr是VAD的過完備字典矩陣，定義如下：

DM=［aM（1，θ1），aM（2，θ2），…，aM（Gr，θGr）］（8）

DM的任一列表示某一特定的方位角和仰角對應的陣列導向向量。即DM在垂直和水平方向上將BS端的AoA角度空間均勻劃分為Gr個離散角度。類似地：

DN=［aN（1，θ1），aN（2，θ2），…，aN（Gt，θGt）］（9）

DN∈CN×Gt在垂直和水平方向上將IRS端的AoD角度空間均勻劃分為Gt個離散角度。Ha∈CGr×Gt為等效信道H在虛擬角域對應的信道，在若干個方位角上具有信道增益。出于精度的考慮，Gr×Gt的值要遠大于信道中的散射路徑的數量，在Ha中只存在少數非零元素表示信道增益［32］。因此，Ha是一個稀疏矩陣，從而可以使用基于壓縮感知算法將信道估計問題轉化為稀疏信道矩陣Ha的恢復問題。

不妨假設傳輸導頻信號x（t）=1，根據式（6）和式（7），接收信號可以重新表述為

Y=［y（0），y（1），…，y（T－1）］=DMHaDHNV+W（10）

式中：T為導頻長度;V=［v（0），v（1），…，v（T－1）］∈CN×T;W=［w（0），w（1），…，w（T－1）］∈CM×T。進一步接收信號矩陣Y∈CM×L可以改寫為向量形式：

y-=vec（YH）=（conj（DM）（VHDN））vec（HHa）+vec（WH）=Θh-+w-（11）

式中：vec（·）表示將矩陣拉直成一個列向量;conj（·）表示將向量1矩陣取共軛。h-=vec（HHa）∈CGrGt×1，表示稀疏的角域信道向量;w-=vec（WH）∈CMT×1，表示噪聲向量;Θ=conj（DM）（VHDN）∈CMT×GrGt表示恢復稀疏向量h-的字典矩陣。可以利用壓縮感知信號恢復算法，對稀疏向量h-進行估計。

2" 信道估計

2.1" 稀疏度與信道估計殘差l2范數關系分析

OMP算法的基本思想是每次選取相關性最高的原子去逼近接收信號，在保證每次在字典矩陣中選取的原子與上一次選擇的原子正交的約束條件下，每次選取最優解，使得算法輸出結果的殘差r的l2范數盡可能小，即

r2=y-－Θh^2lt;ε（12）

式中：·2表示矩陣的l2范數;y-表示接收信號向量;Θ表示字典矩陣;h^為恢復出的稀疏向量;ε為一個足夠小的正數。當式（12）成立時，認為誤差在可以忽略的范圍內，此時接收信號y-是OMP算法所選擇的原子的線性組合。為方便討論，后續用r來表示殘差r的l2范數，即

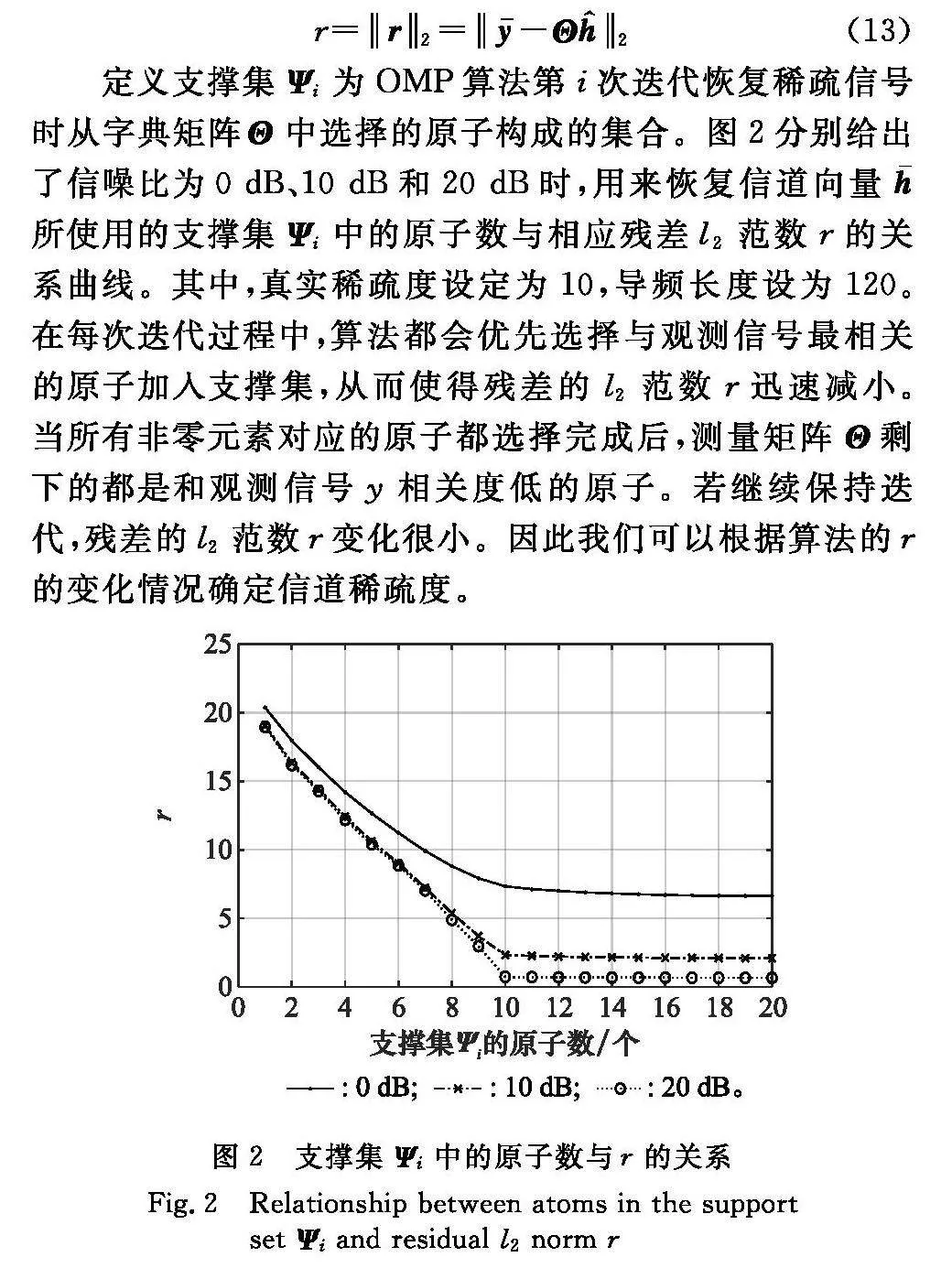
r=r2=y-－Θh^2（13）

定義支撐集Ψi為OMP算法第i次迭代恢復稀疏信號時從字典矩陣Θ中選擇的原子構成的集合。圖2分別給出了信噪比為0 dB、10 dB和20 dB時，用來恢復信道向量h-所使用的支撐集Ψi中的原子數與相應殘差l2范數r的關系曲線。其中，真實稀疏度設定為10，導頻長度設為120。在每次迭代過程中，算法都會優先選擇與觀測信號最相關的原子加入支撐集，從而使得殘差的l2范數r迅速減小。當所有非零元素對應的原子都選擇完成后，測量矩陣Θ剩下的都是和觀測信號y相關度低的原子。若繼續保持迭代，殘差的l2范數r變化很小。因此我們可以根據算法的r的變化情況確定信道稀疏度。

2.2" SACE算法

2.2.1" 算法基本思想

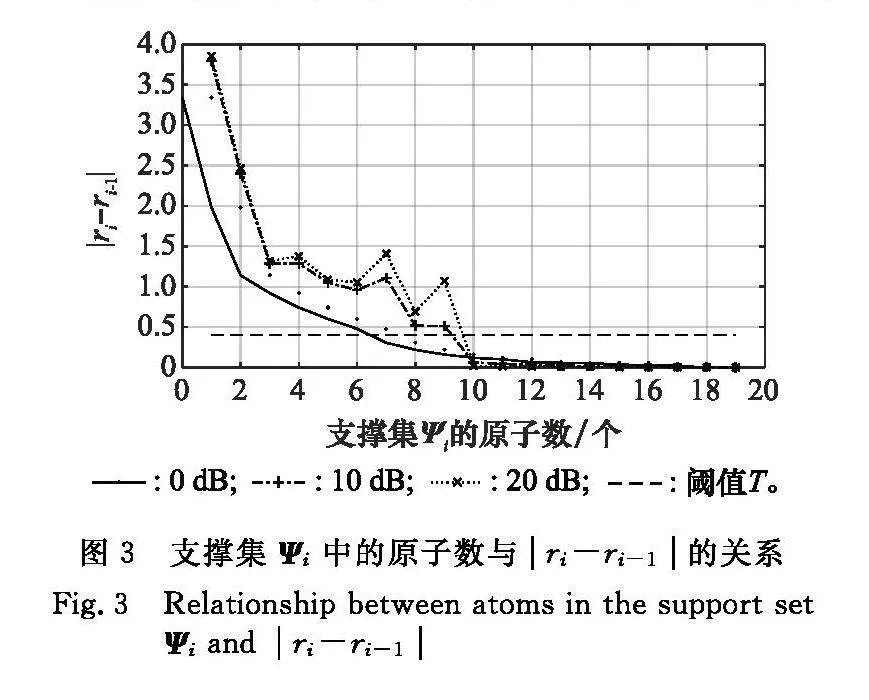
根據上節分析，可以根據殘差變化情況確定稀疏度。但信噪比不同時，r會穩定在不同的值。因此，我們考慮相鄰兩次迭代（支撐集Ψ原子數量相差1）輸出的ri和ri－1的差值。圖3給出了相鄰兩次迭代殘差的差值變化曲線（仿真條件與圖2相同），圖中橫軸仍表示支撐集Ψi中的原子數，縱軸表示殘差l2范數的變化量ri－ri－1，即曲線上的點是當前ri與上一次輸出的殘差ri－1求l2范數并作差所得的結果。

Ψi and ri－ri－1

由圖3可以看出，當選取的支撐集原子數小于真實稀疏度時，殘差變化較大;當支撐集原子數達到真實值10后，殘差變化量迅速下降到很小的值。

基于上述分析，在重構未知稀疏度的信道向量時，可以設定門限T，通過對比相鄰兩次迭代殘差l2范數的變化與門限T的大小確定稀疏度：

ri－ri+1lt;T（14）

式中：ri+1為當前迭代殘差的l2范數（支撐集為Ψi+1）;ri為上一次迭代殘差的l2范數（支撐集為Ψi）;T為迭代終止的閾值。對于未知稀疏度的信道向量，只要當前一次迭代殘差的l2范數和上一次迭代殘差的l2范數差值小于T時，停止迭代，此時支撐集Ψi的原子個數即為信道稀疏度估計值。圖3中的殘差l2范數變化曲線是在毫米波信道環境中仿真獲得的，由此可知，對于IRS輔助的毫米波MIMO系統，T應當取小于0.5的值才能使得算法估計的稀疏度較為準確。此外，在低信噪比情況下曲線（例如圖2中0 dB的曲線）較為平緩，因此T的取值同樣不應該過小，否則會出現估計稀疏度偏大的情況。

隨著BS側的天線數量以及IRS反射元件數量的增加，信道系數的數量和信道稀疏度也會隨之變大［33］。在信道稀疏度較大的情況下，每次迭代都計算殘差的l2范數并使用下式進行判決：

rL－rL+slt;Ts（15）

式中：兩次對比的殘差l2范數相差原子數為s。

這樣無疑降低了估計效率。從圖2和圖3可以看出，在當前支撐集Ψi+1中的原子數小于信道真實稀疏度時，殘差l2范數曲線是單調遞減的，而且每次殘差l2范數的變化都在閾值T以上，因此可以通過比較任意兩次迭代殘差l2范數的差來判斷是否終止迭代。

2.2.2" SACE算法

算法 1" SACE

輸入" 字典矩陣Θ∈CMT×GrGt，接收信號向量y-，步長參數S0

輸出" 稀疏信道向量h^，信道稀疏度P^s

設初始迭代次數i=1，初始殘差r0=y-，初始列序號集合φi=，初始支撐集Ψ0=，判決節點L=S0

步驟 1" 找到列序號λi，使得：λi=arg maxj=1，2，…，GtGr〈Θjri－1〉，令φi=φi－1∪{λi}，支撐集Ψi=Ψi－1∪Θλi

步驟 2" 計算當前殘差ri：ri=y-－Ψi（ΨTiΨi）－1ΨTiy-，令i=i+1

步驟 3" 當ilt;L時，跳轉回步驟1，繼續迭代;當i=L時，跳轉至步驟4

步驟 4" 計算rL－S0－rL（ri=y-－Ψi（ΨTiΨi）－1ΨTiy-2），若rL－S0－rL≥TS0，令L=L+S0，返回步驟1繼續迭代;否則，結束迭代，輸出h^=h^L，信道稀疏度P^s=L。

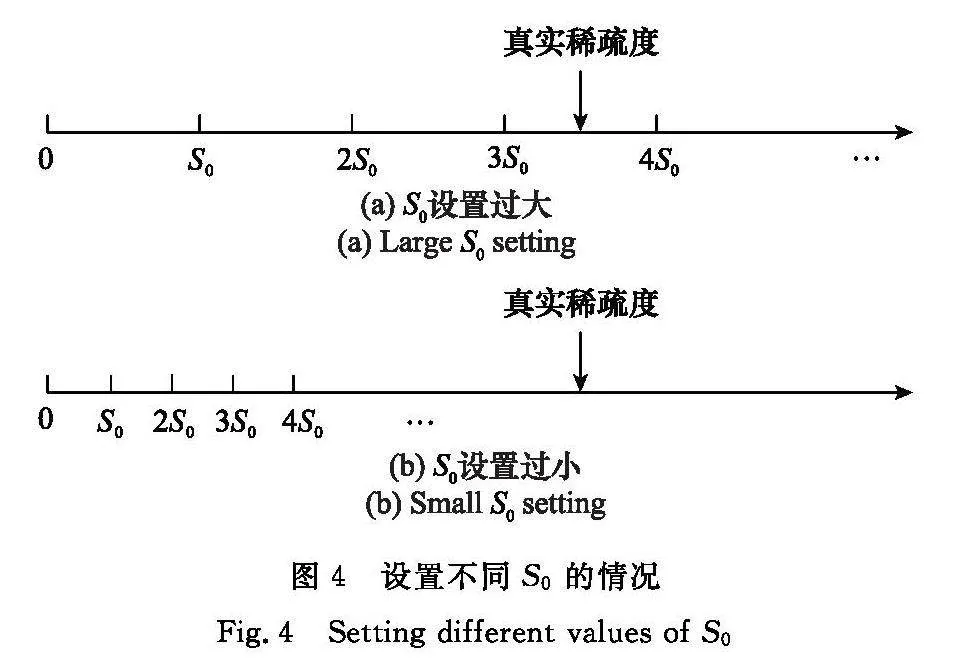
在恢復稀疏信道時，由于定義了單個步長參數S0，如圖4所示，算法將信道稀疏度離散化為大小為S0的區間，每過S0次迭代，進行一次判決，若符合式（15），則輸出信道稀疏度P^s=nS0（n=1，2，3，…），同時給出重構的稀疏信道向量h^。若S0設置過大，誤差會增大，如圖4（a）所示，算法將在4S0處停止迭代，重構稀疏信道時帶入了過多冗余原子;若S0設置過小，如圖4（b）所示，需要多次比較判斷，收斂速度慢。為了解決上述問題，S0的值可以在迭代中不斷改變。文獻［34］引入了變步長的思想，利用擬合的指數函數值作為壓縮感知算法選擇原子時的步長，其仿真結果表明可以獲得比固定的S0更好的估計結果。但是在毫米波信道下采用變步長的做法，每次恢復稀疏信道需要從頭開始選取原子，并且每次迭代需要額外計算S0，估計時長很可能已經超過信道相干時間，無法利用互易性獲取下行鏈路的CSI。

為了解決這一問題，我們提出了如下的幀結構。

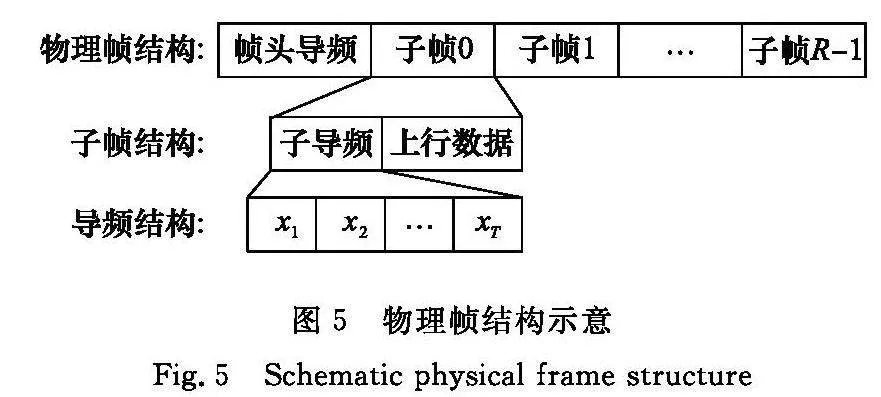
圖5給出了IRS輔助系統上行鏈路信道估計使用的物理層幀結構。一個信號幀由幀頭導頻和R個數據子幀組成，其中幀頭為一段導頻序列，數據子幀由子導頻序列和數據兩部分組成，數據子幀的長度小于信道相干時間。

由于BS和IRS都安裝在固定位置，且空氣中存在的散射體有限，毫米波信道中存在的散射路徑數量服從慢衰落，且散射路徑數量在較長時間內（R個數據子幀持續的時間）不會發生變化［21］。因此，可以使用幀頭導頻首先估計出信道的大致稀疏度P^s，并給出一個P^s大小的支撐集。在后續的R個數據子幀到達BS時，每個數據子幀分別進行一次信道估計，獲取準確的信道估計結果。

我們將信道估計分為兩個階段進行：第一階段，使用較大的S0快速獲取稀疏度P^s，第二階段使用較小的S1，對每個子幀分別進行稀疏度修正同時完成信道估計，如圖6所示。

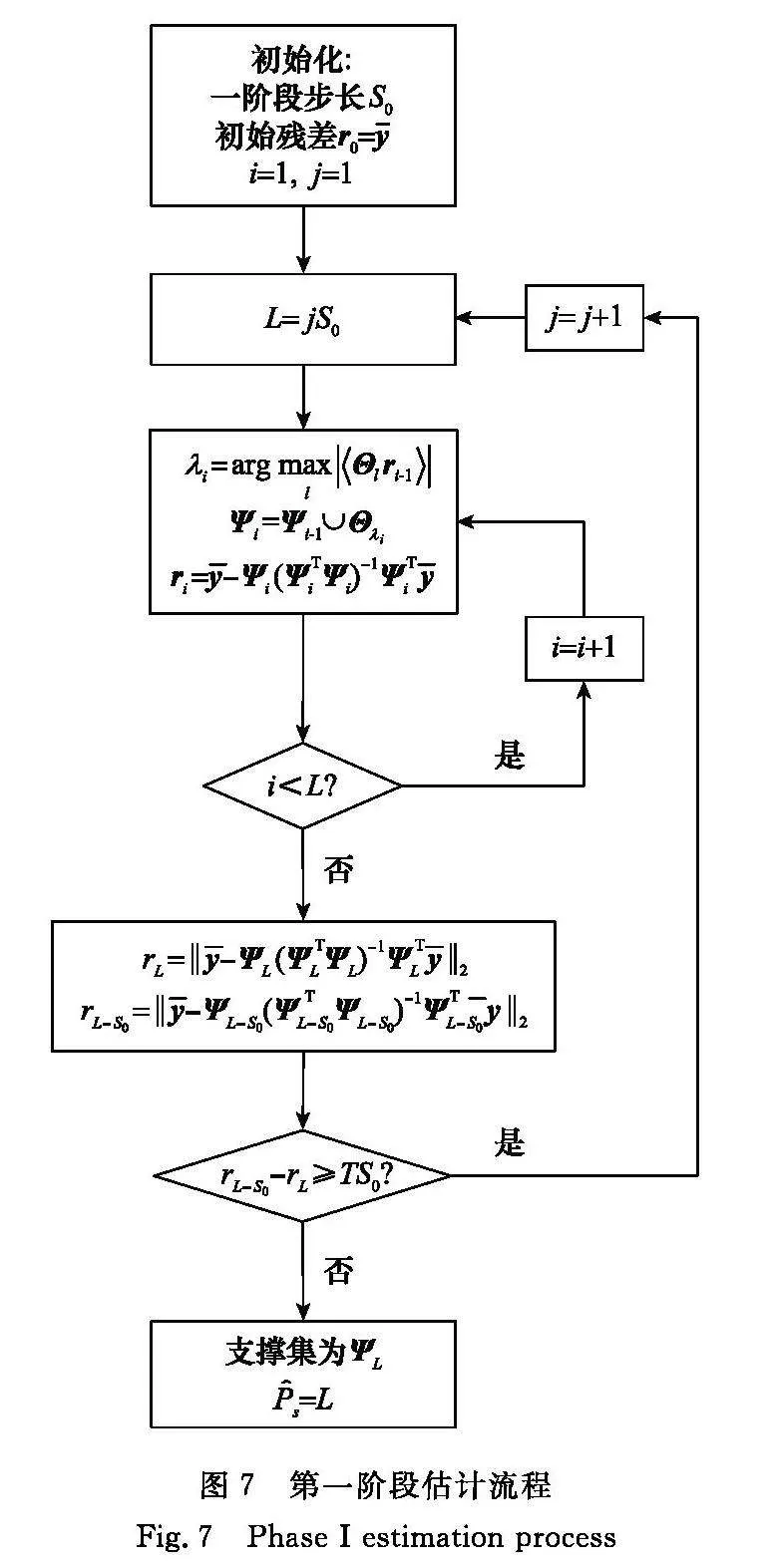
第一階段的估計流程如圖7所示。

每選取S0個原子時，計算殘差的l2范數，并使用式（15）進行一次判決，若滿足式（15），則輸出P^s和Ψ，若不滿足則繼續選取S0個原子，進行下一次判決，直至滿足為止。對于毫米波頻段，BS-IRS信道以及IRS-UE信道一般分別存在3～5條散射徑［22］，因此在第一階段中，參數S0值的區間設置為S0∈［3，5］，這樣可以保證第一階段估計的稀疏度誤差不會過大，同時提高了算法效率。

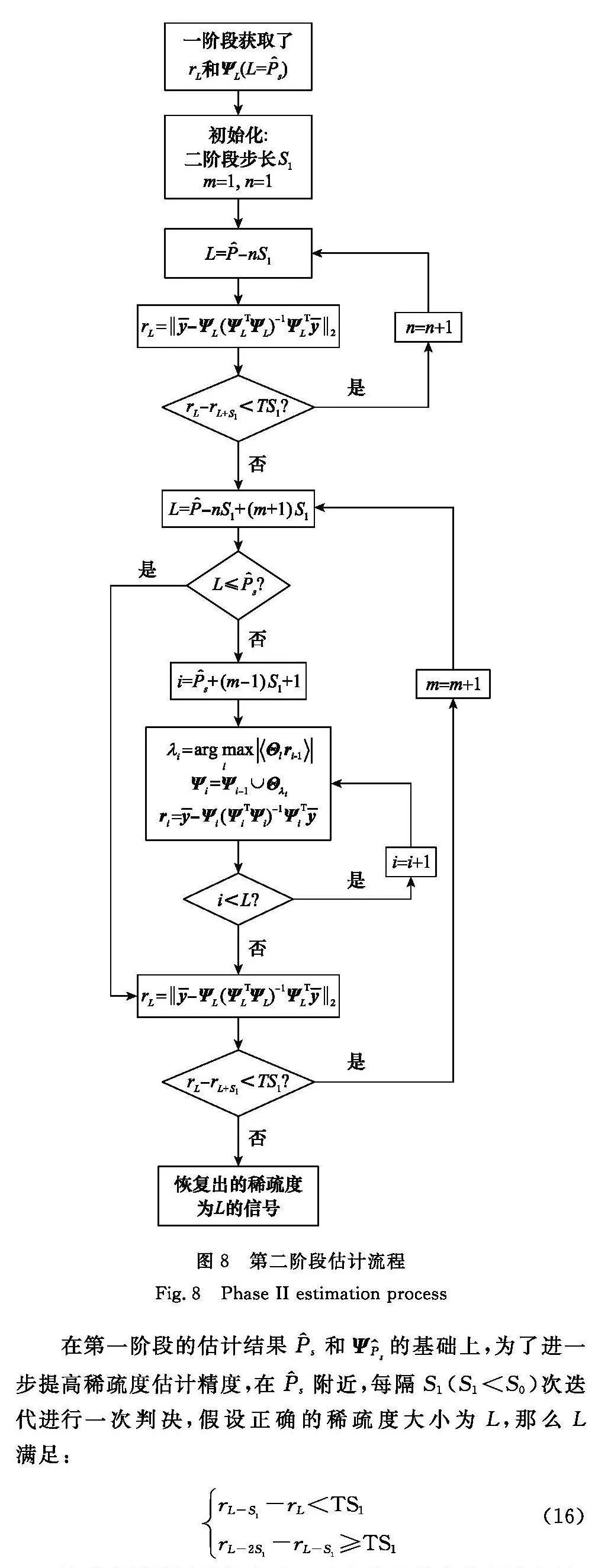
第二階段的具體流程如圖8所示。

在第一階段的估計結果P^s和ΨP^s的基礎上，為了進一步提高稀疏度估計精度，在P^s附近，每隔S1（S1lt;S0）次迭代進行一次判決，假設正確的稀疏度大小為L，那么L滿足：

rL－S1－rLlt;TS1rL－2S1－rL－S1≥TS1（16）

這樣臨界位置的稀疏度L對應的是精確的信道向量，可恢復出稀疏信道向量h^。

3" 仿真與分析

本節通過仿真分析評估所提方案的性能，并與傳統最小二乘（least square， LS）信道估計算法、SAMP和已知稀疏度的OMP算法進行對比。仿真中，BS與UE使用IRS輔助通信，BS處設定為M=16（4×4）的UPA，IRS處設定為反射元件數N=64（8×8）的UPA。BS-IRS信道和IRS-UE信道中均存在視距徑（line of sight， LoS）和非LoS徑，萊斯因子設為13.2 dB［14］。此外，IRS的相移矩陣中相位為［－π/2，π/2］區間內隨機生成。仿真中假定一個物理幀內信道稀疏度不變。幀頭導頻用作第一階段估計，數據子幀的導頻用作第二階段估計。

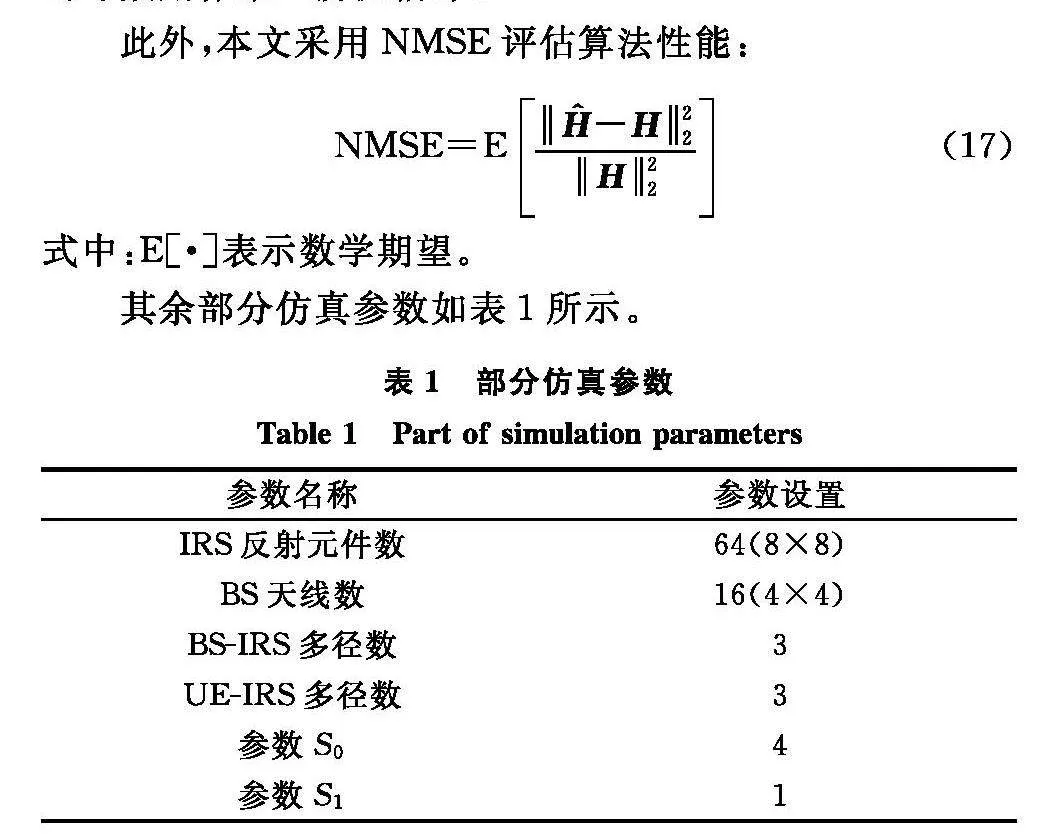
此外，本文采用NMSE評估算法性能：

NMSE=EH^－H22H22（17）

式中：E［·］表示數學期望。

其余部分仿真參數如表1所示。

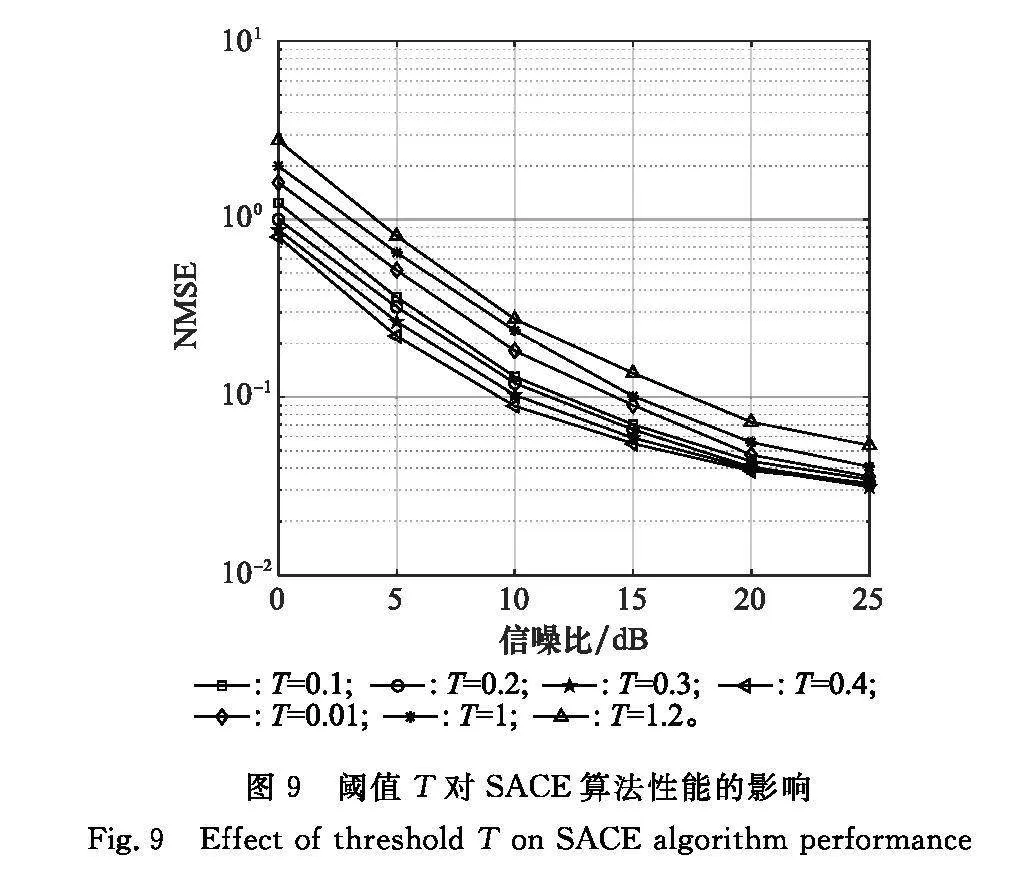
圖9給出了多種閾值T取值下的信噪比-NMSE曲線。由圖中可以看出，T取值過小或者過大會降低算法性能，當T取值為0.1～0.4時，算法性能最好。在此后的對比仿真中，T取值為0.4。

圖10給出了本文提出的SACE算法與其他算法的信噪比-NMSE曲線。由于LS算法導頻序列P的長度應當滿足PLength≥MN，因此LS對應的導頻長度設為1 024，其他算法導頻長度為120。可以看出，各算法的均方誤差均隨著信噪比增加而降低。傳統的LS算法性能受信噪比影響較大，在信噪比低時性能最差。SAMP算法也能對未知稀疏度信道向量進行恢復，但是性能較差。在信噪比低于20 dB時，本文提出的SACE算法與文獻［29］中已知稀疏度的OMP算法約有1 dB的性能差距，但在信噪比大于20 dB時二者性能一致，說明本文提出的算法，對于稀疏度未知的信道性能良好。

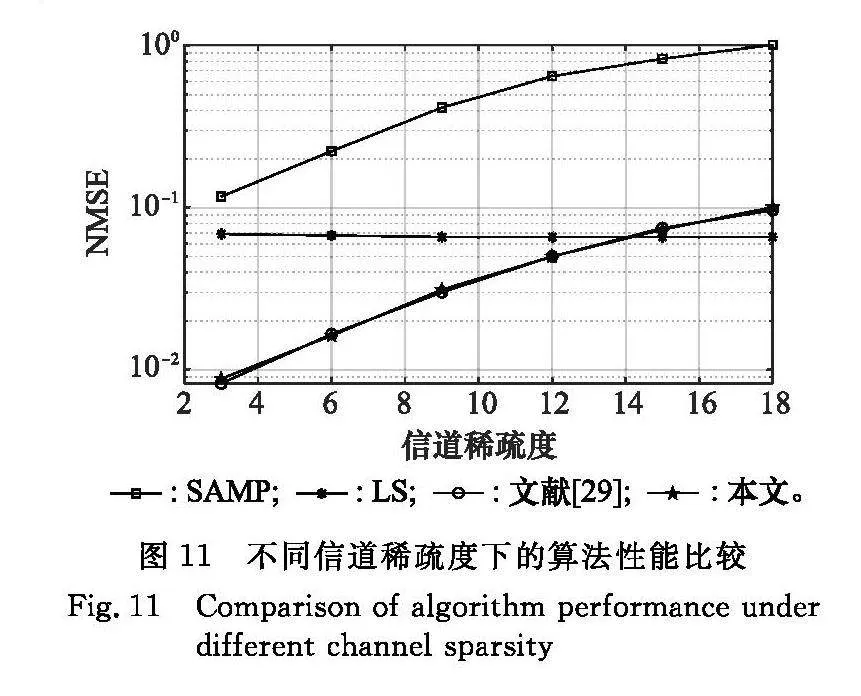
圖11給出了信噪比為20 dB時，不同信道估計算法的NMSE隨信道稀疏度的變化情況。可以看出，各算法NMSE隨著信道稀疏度的增加而增大。其中，文獻［29］已知稀疏度的OMP算法和本文提出的SACE算法在信道不同稀疏度下對應的NMSE均小于SAMP算法，而且SACE算法的NMSE與已知稀疏度的OMP算法極為接近，說明SACE算法具有魯棒性，可以很好地適配未知稀疏度的信道環境。

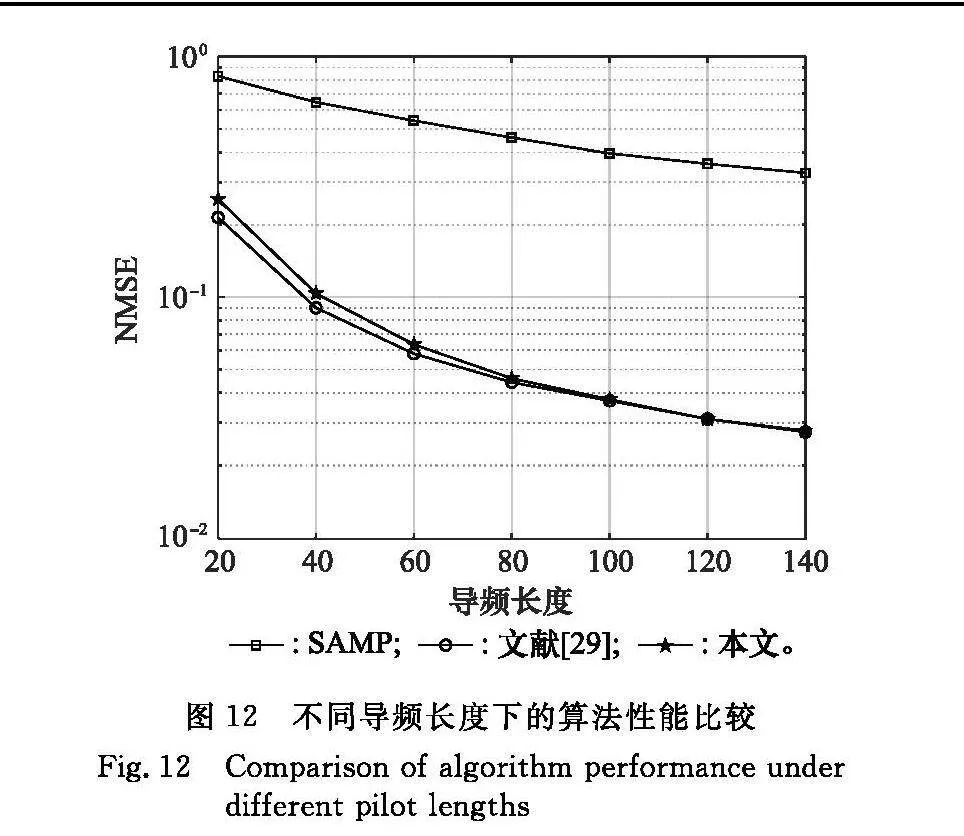
圖12給出了信噪比為20 dB，信道稀疏度為9時，各算法的NMSE隨導頻長度的變化情況。可以看出，NMSE隨著導頻長度的增加而減小。其中，SACE算法的NMSE明顯低于SAMP算法的。此外，當導頻長度大于80時，對應的NMSE與文獻［29］中已知稀疏度的OMP算法基本重合。進一步說明了本文提出的SACE算法在即使不具備信道稀疏度先驗信息的情況下仍具有良好的性能。

4" 結" 論

本文針對未知稀疏度信道的估計問題，提出了一種SACE算法，在第一階段估計稀疏度，并儲存當前所估計的稀疏度對應的支撐集，在第二階段對該支撐集進行修改，最終獲取精確的信道估計結果。仿真結果表明，本文所提方案可以恢復出稀疏度未知的信道，且性能良好。

參考文獻

［1］ WU Q Q， ZHANG R. Intelligent reflecting surface enhanced wireless network： joint active and passive beamforming design［C］∥Proc.of the IEEE Global Communications Conference， 2018.

［2］ TAN X， SUN Z， KOUTSONIKOLAS D， et al. Enabling indoor mobile millimeter wave networks based on smart reflect-arrays［C］∥Proc.of the IEEE Conference on Computer Communications， 2018： 270278.

［3］ HU S， RUSEK F， EDFORS O. Beyond massive-MIMO： the potential of data-transmission with large intelligent surfaces［J］. IEEE Trans.on Signal Processing， 2018， 66（10）： 27462758.

［4］ WU Q Q， ZHANG R. Towards smart and reconfigurable environment： intelligent reflecting surface aided wireless network［J］. IEEE Communications Magazine， 2020， 58（1）： 106112.

［5］ WU Q Q， ZHANG S W， ZHENG B X， et al. Intelligent reflecting surface aided wireless communications： a tutorial［J］. IEEE Trans.on Communications， 2021， 69（5）： 33133351.

［6］ YANG Y F， ZHENG B X， ZHANG S W， et al. Intelligent reflecting surface meets OFDM： protocol design and rate maximizati-on［J］. IEEE Trans.on Communications， 2020， 68（7）： 45224535.

［7］ ZHENG B X， ZHAN R. Intelligent reflecting surface enhanced OFDM： channel estimation and reflection optimization［J］. IEEE Wireless Communications Letters， 2020， 9（4）： 518522.

［8］ ZHENG B X， YOU C S， ZHANG R. Fast channel estimation for IRS assisted OFDM［J］. IEEE Wireless Communications Letters， 2021， 10（3）： 580584.

［9］ ZHENG B， YOU C S， ZHANG R. Intelligent reflecting surface assisted multiuser OFDMA： channel estimation and training design［J］. IEEE Trans.on Wireless Communications， 2020， 19（12）： 83158329.

［10］ JIANG W H， CHEN B X， ZHAO J， et al. Joint active and passive beamforming design for the IRS assisted MIMOME-OFDM secure communications［J］. IEEE Trans.on Vehicular Technology， 2021， 70（10）： 1036910381.

［11］ ZHANG S W， ZHANG R. Capacity characterization for intelligent reflecting surface aided MIMO communication［J］. IEEE Journal on Selected Areas in Communications， 2020， 38（8）： 18231838.

［12］ PAN C H， REN H， WANG K Z， et al. Multicell MIMO communications relying on intelligent reflecting surfaces［J］. IEEE Trans.on Wireless Communications， 2020， 19（8）： 52185233.

［13］ OZDOGAN O， BJORNSON E， LARSSONE G. Using intelligent reflecting surfaces for rank improvement in MIMO comm-unications［C］∥Proc.of the IEEE International Conference on Acoustics， Speech and Signal Processing， 2020： 91609164.

［14］ ZHENG B X， WU Q Q， ZHANG R. Intelligent reflecting surface-assisted multiple access with user pairing： NOMA or OMA？［J］. IEEE Communications Letters， 2020， 24（4）： 753757.

［15］ YANG G， XU X Y， LIANG Y C. Intelligent reflecting surface assisted nonorthogonal multiple access［C］∥Proc.of the IEEE Wireless Communications and Networking Conference， 2020.

［16］ DING Z， POOR H V. A simple design of IRS-NOMA transmission［J］. IEEE Communications Letters， 2020， 24（5）： 11191123.

［17］ MU X D， LIU Y W， GUO L， et al. Exploiting intelligent reflecting surfaces in NOMA networks： joint beamforming optimization［J］. IEEE Trans.on Wireless Communications， 2020， 19（10）： 68846898.

［18］ 齊永磊， 陳西宏， 袁迪喆. SC-FDE系統中基于UW的聯合信道估計均衡算法［J］. 系統工程與電子技術， 2022， 44（10）： 32583265.

QI Y L， CHEN X H， YUAN D Z. Joint channel estimation and equalization algorithm based on UW for SC-FDEsystem［J］. Systems Engineering and Electronics， 2022， 44（10）： 32583265.

［19］ LIU H， ZHANG J Y， WU Q Q， et al. ADMM based channel estimation for RISs aided millimeter wave communications［J］. IEEE Communications Letters， 2021， 25（9）： 28942898.

［20］ MAO Z， PENG M， LIU X. Channel estimation for reconfigurable intelligent surface assisted wireless communication systems in mobility scenarios［J］. China Communications， 2021， 18（3）： 2938.

［21］ HE J， WYMEERSCH H， JUNTTI M. Channel estimation for RIS-aided mmWave MIMO systems via atomic norm minimization［J］.IEEE Trans.on Wireless Communications， 2021， 20（9）： 57865797.

［22］ HE J， LEINONEN M， WYMEERSCH H， et al. Channel estimation for RIS-aided mmWave MIMO systems［C］∥Proc.of the IEEE Global Communications Conference， 2020.

［23］ MA X Y， CHEN Z， CHEN W J， et al. Joint channel estimation and data rate maximization for intelligent reflecting surface assisted terahertz MIMO communication systems［J］. IEEE Access， 2020， 8： 9956599581.

［24］ MIRZA J， ALI B. Channel estimation method and phase shift design for reconfigurable intelligent surface assisted MIMO networks［J］. IEEE Trans.on Cognitive Communications and Networking， 2021， 7（2）： 441451.

［25］ WEI X H， SHEN D C， DAI L L. Channel estimation for RIS assisted wireless communications—part II： an improved solution based on double-structured sparsity［J］. IEEE Communications Letters， 2021， 25（5）： 14031407.

［26］ WAN Z W， GAO Z， GAO F F， et al. Terahertz massive MIMO with holographic reconfigurable intelligent surfaces［J］. IEEE Trans.on Communications， 2021， 69（7）： 47324750.

［27］ ARDAH K， GHEREKHLOO S， HAARDTM， et al. TRICE： a channel estimation framework for RIS-aided millimeter-waveMIMO systems［J］. IEEE Signal Processing Letters， 2021， 28： 513517.

［28］ WAN Z W， GAO Z， ALOUINI M S. Broad-band channel estimation for intelligent reflecting surface aided mmWave massive MIMO systems［C］∥Proc of the IEEE International Conference on Communications， 2020， 27： 905909.

［29］ WANG P L， FANG J， DUAN H P， et al. Compressed channel estimation for intelligent reflecting surface assisted millimeter Wave systems［J］. IEEE Signal Processing Letters， 2020， 27： 905909.

［30］ ALEXANDROPOULOS" G C， VLACHOS E. A hardware architecture for reconfigurable intelligent surfaces with minimal active elements for explicit channel estimation［C］∥Proc.of the IEEE International Conference on Acoustics， Speech and Signal Processing， 2020： 91759179.

［31］ MISHRA" D， JOHANSSON H. Channel estimation and low-complexity beamforming design for passive intelligent surface assisted MISO wireless energy transfer［C］∥Proc.of the IEEE International Conference on Acoustics， Speech and Signal Processing， 2019： 46594663.

［32］ HE Z Q， YUAN X. Cascaded channel estimation for large intelligent metasurface assisted massive MIMO［J］. IEEE Wireless Communications Letters， 2020， 9（2）： 210214.

［33］ NADEEM Q， ALWAZANI H， KAMMOUN A， et al. Intelligent reflecting surface assisted multiuser MISO communication： channel estimation and beamforming design［J］. IEEE Open Journal of the Communic-ations Society， 2020， 1（1）： 661680.

［34］ 吳夢行， 伍飛云， 楊坤德， 等. 改進的稀疏度自適應多路徑匹配追蹤算法［J］. 哈爾濱工程大學學報， 2021， 42（11）： 16111617.

WU M X， WU F Y， YANG K D， et al. Improved sparsity adaptive multipath matching pursuit algorithm［J］. Journal of Harbin Engineering University， 2021， 42（11）： 16111617.

作者簡介

劉" 剛（1977—），男，教授，博士，主要研究方向為寬帶無線傳輸技術。

李雨航（1996—），男，碩士研究生，主要研究方向為寬帶無線通信、智能反射面。

楊慶鑫（1995—），男，碩士，主要研究方向為寬帶無線通信、大規模多輸入多輸出。

郭" 漪（1977—），女，副教授，博士，主要研究方向為寬帶無線通信傳輸系統。