基于綜合變軌的高軌遠(yuǎn)程自主交會(huì)規(guī)劃方法

摘" 要：

基于近圓偏差線(xiàn)性方程研究了高軌遠(yuǎn)程交會(huì)問(wèn)題，基于面內(nèi)三脈沖變軌策略建立了雙層非線(xiàn)性規(guī)劃模型。外層采用粒子群算法對(duì)第1個(gè)和第2個(gè)脈沖緯度幅角進(jìn)行尋優(yōu)，對(duì)傳統(tǒng)固定在遠(yuǎn)地點(diǎn)或近地點(diǎn)的方法進(jìn)行改進(jìn)。在確定第1個(gè)和第2個(gè)脈沖緯度幅角后，內(nèi)層采用近圓偏差線(xiàn)性方程，快速迭代求解第3個(gè)脈沖緯度幅角和3次脈沖的速度增量。仿真結(jié)果表明，所提規(guī)劃方法可用更小的燃料代價(jià)在指定時(shí)間內(nèi)到達(dá)指定的變軌終端，具有工程應(yīng)用價(jià)值。

關(guān)鍵詞：

高軌; 遠(yuǎn)程交會(huì); 自主規(guī)劃; 近圓偏差線(xiàn)性方程

中圖分類(lèi)號(hào)：

V 448.23

文獻(xiàn)標(biāo)志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.07.29

Far-range autonomous rendezvous planning method of geosynchronous

orbit based on hybrid maneuvers

XU Guangde*， HE Jingjing

（Beijing Institute of Spacecraft System Engineering， Beijing 100094， China）

Abstract：

Far-range rendezvous problem of geosynchronous orbit is studied based on the linear equation of near-circular deviation， and a two-layer nonlinear programming model is established based on the in-plane 3-pulse manuveur strategy. In the outer layer， the particle swarm optimization algorithm is used to optimize the arugment angle of the first and second pulses， which improves the traditional method of fixing at apogee or perigee. After determining the arugment angle of the first pulse and the second pulse， the inner layer uses the near-circular deviation linear equation to solve the arugment angle of the third pulse and the speed increment of the three pulses quickly. Simulation results show that the proposed planning method can reach the designated terminal in the specified time with less fuel cost， and has engineering application value.

Keywords：

geosynchronous orbit; far-range rendezvous; autonomous planning; near-circular deviation linear equation

0" 引" 言

高軌是高價(jià)值衛(wèi)星聚集地，高軌在軌服務(wù)［18］等任務(wù)發(fā)展均提出了自主交會(huì)需求。與近地空間載人交會(huì)對(duì)接類(lèi)似，交會(huì)過(guò)程由遠(yuǎn)程交會(huì)和近程接近兩個(gè)階段組成。遠(yuǎn)程交會(huì)自主規(guī)劃是指采用一定的數(shù)學(xué)手段，規(guī)劃變軌系列（變軌次數(shù)、變軌位置、脈沖大小與方向），使航天器在預(yù)定的時(shí)刻到達(dá)指定的位置。

遠(yuǎn)程交會(huì)規(guī)劃主要分為特殊點(diǎn)變軌和綜合變軌兩種策略。特殊點(diǎn)變軌指遠(yuǎn)近點(diǎn)調(diào)整軌道高度、在軌道面交點(diǎn)處修正軌道面差，在載人交會(huì)對(duì)接中廣泛應(yīng)用。綜合變軌［714］指變軌點(diǎn)不固定在特殊點(diǎn)，主要包括多圈Lambert交會(huì)和基于近圓偏差線(xiàn)性方程兩種方法。

遠(yuǎn)程交會(huì)規(guī)劃在近地軌道研究較多［1517］，對(duì)高軌遠(yuǎn)程交會(huì)規(guī)劃問(wèn)題研究較少。文獻(xiàn)［18］采用被動(dòng)安全共面橢圓交會(huì)策略，設(shè)計(jì)了300 km以?xún)?nèi)的機(jī)動(dòng)路徑。文獻(xiàn)［1920］研究了地球同步軌道（geosynchronous Earth orbit， GEO）目標(biāo)近距離交會(huì)下的軌道安全和碰撞規(guī)避問(wèn)題。文獻(xiàn)［21］針對(duì)GEO遠(yuǎn)距離長(zhǎng)時(shí)間變軌規(guī)劃問(wèn)題，提出霍曼與Lambert結(jié)合的四脈沖變軌方法，首先在遠(yuǎn)地點(diǎn)、近地點(diǎn)施加兩次切向脈沖，進(jìn)入橢圓漂移軌道，利用軌道動(dòng)力學(xué)特性自然漂星。漂星至目標(biāo)附近時(shí)，進(jìn)行Lambert雙脈沖變軌（均有切向、徑向分量）進(jìn)入目標(biāo)軌道，克服了多圈Lambert變軌計(jì)算量大、求解復(fù)雜的難點(diǎn)。文獻(xiàn)［22］針對(duì)GEO在軌服務(wù)，對(duì)比分析了霍曼變軌式、機(jī)動(dòng)漂移式、徑向機(jī)動(dòng)式和蘭伯特變軌式4種工程上常用的軌道交會(huì)策略，采用遺傳算法對(duì)多目標(biāo)在軌服務(wù)問(wèn)題進(jìn)行優(yōu)化，得到了任務(wù)時(shí)間約束下的最優(yōu)飛行路徑。文獻(xiàn)［23］面向高軌遠(yuǎn)程交會(huì)需求，提出一種基于近圓線(xiàn)性偏差方程的四脈沖變軌規(guī)劃方法，其中3個(gè)切向脈沖用于調(diào)相，1個(gè)法向脈沖用于調(diào)整軌道面。3個(gè)切向脈沖分別在遠(yuǎn)地點(diǎn)附近、近地點(diǎn)附近、遠(yuǎn)地點(diǎn)附近施加，本質(zhì)上還是特殊點(diǎn)變軌，且總變軌時(shí)間限定在4天，總?cè)Υ螢?圈，為特殊應(yīng)用工況，對(duì)變軌總時(shí)間、相位差等適應(yīng)性差。

本文采用基于近圓偏差線(xiàn)性方程的綜合變軌策略，在文獻(xiàn)［23］的基礎(chǔ)上對(duì)高軌遠(yuǎn)程交會(huì)規(guī)劃方法進(jìn)行了改進(jìn)，設(shè)計(jì)了內(nèi)外兩層規(guī)劃方法。外層以前兩次變軌緯度幅角為優(yōu)化變量，采用粒子群優(yōu)化算法進(jìn)行快速尋優(yōu)，在確定了前兩次脈沖位置后，內(nèi)層基于近圓偏差線(xiàn)性方程迭代求解得到三切向脈沖變軌策略。與文獻(xiàn)［23］提出的方法及STK軟件仿真結(jié)果進(jìn)行了對(duì)比，驗(yàn)證了本文方法的有效性和優(yōu)越性。

1" 近圓偏差線(xiàn)性方程

在高軌遠(yuǎn)程交會(huì)段，與目標(biāo)之間距離達(dá)到上萬(wàn)千米，與軌道半徑相近，線(xiàn)性化的C-W方程不再適用，可采用近圓偏差線(xiàn)性方程［10］。

首先，定義參考軌道柱坐標(biāo)系［7］，以地心為原點(diǎn)，r為航天器地心矢量r在參考軌道平面內(nèi)的投影，θ為投影的緯度幅角，z為沿軌道法線(xiàn)方向投影，如圖1所示。

航天器在柱坐標(biāo)系OE－rθz的動(dòng)力學(xué)方程［7］為

r¨=－μr2+rθ" ·2+ar

rθ" ¨=－2r·θ·+at

z¨=－μr3z+az （1）

設(shè)vt=rθ" ·，vr=r·，vz=z·z·，參考航天器在柱坐標(biāo)系中的狀態(tài)為［r0，r0θ，0，0，vt，0］T。相對(duì)狀態(tài)定義為航天器狀態(tài)與參考航天器狀態(tài)之差，X=［Δr，r0Δθ，Δz，Δvr，Δvt，Δvz］T，Δr，Δθ，Δz，Δvr，Δvt和Δvz分別為航天器相對(duì)于參考軌道的徑向位置差、緯度幅角差、法向位置差、徑向速度差、跡向速度差和法向速度差，

將參考軌道和所研究航天器的動(dòng)力學(xué)方程作差，保留一階小量并略去高階小量，得到近圓偏差線(xiàn)性方程。

Δr·=Δvr

Δθ·=－ω0Δrr0+ω0Δvtv0

Δz·z·=Δvz

Δv·r=ω20Δr+2ω0Δvt+Δar

Δv·t=－ω0Δvr+Δat

Δv·z=－ω20Δz+Δaz" （2）

式中：Δar，Δat和Δaz表示加速度差。ω0，r0分別為參考軌道角速度及半徑。

考慮t1，t2，…，tn時(shí)刻一系列脈沖Δv1，Δv2，…，Δvn，相對(duì)運(yùn)動(dòng)方程的狀態(tài)方程［7］表達(dá)形式為

X（tf）=Φ（tf，t0）X（t0）+∑ni=1Φv（tf，ti）Δvi（3）

式中：

Φ（tf，t0）=2－cos Δθ000sin Δθ0ω0－2（cos Δθ0－1）ω00

2sin Δθ0－3Δθ0102（cos Δθ0－1）ω04sin Δθ0－3Δθ0ω00

00cos Δθ000sin Δθ0ω0

ω0sin Δθ000cos Δθ02sin Δθ00

ω0（cos Δθ0－1）00－sin Δθ0－1+2cos Δθ00

00－ω0sin Δθ000cos Δθ0（4）

Φv（tf，ti）=sin Δθiω0－2（cos Δθi－1）ω00

2（cos Δθi－1）ω04sin Δθi－3Δθiω00

00sin Δθiω0

cos Δθi2sin Δθi0

－sin Δθi－1+2cos Δθi0

00cos Δθi（5）

2" 高軌遠(yuǎn)程交會(huì)雙層規(guī)劃方法

2.1" 規(guī)劃模型

首先，建立高軌遠(yuǎn)程交會(huì)的非線(xiàn)性規(guī)劃模型，包括設(shè)計(jì)變量、約束條件、目標(biāo)函數(shù)等［2425］。

（1） 設(shè)計(jì)變量

設(shè)計(jì)變量包括3次切向變軌的緯度幅角和速度增量。

X=［u1 Δv1 u2 Δv2 u3 Δv3］（6）

式中：ui為各變軌點(diǎn)的緯度幅角;Δvi為各次切向變軌速度增量。

（2） 約束條件

終端約束為變軌終端與目標(biāo)的相對(duì)位置和相對(duì)速度滿(mǎn)足期望條件：

ρ=ρd

ρ·=ρ·d（7）

光照條件約束為接近時(shí)刻的太陽(yáng)光照角滿(mǎn)足順光條件：

θsun=arccosrlos·rsun|rlos||rsun|≤60°（8）

（3） 目標(biāo)函數(shù)

為實(shí)現(xiàn)燃料最優(yōu)，優(yōu)化目標(biāo)函數(shù)為總變軌速度增量最小：

f=∑3i=1|vi|（9）

2.2" 內(nèi)外雙層規(guī)劃求解方法

上述對(duì)高軌目標(biāo)接近觀測(cè)的任務(wù)規(guī)劃模型進(jìn)行了建模，本節(jié)提出基于粒子群算法和近圓偏差線(xiàn)性方程的內(nèi)外雙層規(guī)劃求解策略。計(jì)算流程如圖2所示。

2.2.1" 外層優(yōu)化算法

外層采用粒子群算法對(duì)前兩次變軌點(diǎn)的緯度幅角進(jìn)行尋優(yōu)，目標(biāo)函數(shù)為總的速度增量，由內(nèi)層求解得出。

粒子群算法具體流程參見(jiàn)文獻(xiàn)［2629］。將每個(gè)個(gè)體定義為一個(gè)“粒子”，假設(shè)群體包括m個(gè)粒子，每個(gè)粒子為一個(gè)潛在解。在尋優(yōu)迭代過(guò)程中，粒子的速度和位置按照下式進(jìn)行更新：

vk+1id=ωvkid+c1r1（pid－zkid）+c2r2（pgd－zkid）（10）

zk+1id=zkid+vk+1id（11）

式中：k為迭代次數(shù);i=1，2，…，m;d=1，2，…，D;r1和r2為［0，1］的隨機(jī)數(shù);c1和c2為加速因子。zi=（zi1，zi2，…，ziD），vi=（vi1，vi2，…，vid，…，viD）為第i個(gè)粒子位置和速度;pi=（pi1，pi2，…，pid，…，piD）為當(dāng)前最優(yōu)位置;pg=（pg1，pg2，…，pgd，…，pgD）為整個(gè)過(guò)程中找到的最優(yōu)位置。

慣性權(quán)重ω負(fù)責(zé)對(duì)布局最優(yōu)和全局最優(yōu)進(jìn)行權(quán)衡：

ω=ωmax－ωmax－ωminkmax·k（12）

式中：ωmax為初始權(quán)重;ωmin為最終權(quán)重;kmax為最大迭代次數(shù);k為當(dāng)前迭代次數(shù)。

基于本文優(yōu)化問(wèn)題的特點(diǎn)，設(shè)置粒子群優(yōu)化參數(shù)如表1所示。

2.2.2" 內(nèi)層優(yōu)化算法

在外層通過(guò)粒子群算法優(yōu)化得到第1次和第2次變軌的緯度幅角后，內(nèi)層采用近圓偏差線(xiàn)性方程迭代求解3次變軌的速度增量和第3次脈沖的緯度幅角［7，13，23，28］。

步驟 1" 設(shè)置初始參數(shù)，確定追蹤飛行器初始軌道參數(shù)、遠(yuǎn)距離導(dǎo)引瞄準(zhǔn)點(diǎn)期望軌道參數(shù)、初始圈次、終端圈次、終端時(shí)刻;

步驟 2" 根據(jù)初始軌道和瞄準(zhǔn)點(diǎn)軌道設(shè)置參考圓軌道參數(shù);

步驟 3" 仿真目標(biāo)星運(yùn)行至瞄準(zhǔn)點(diǎn)時(shí)刻tA，計(jì)算瞄準(zhǔn)點(diǎn)和參考軌道間的相對(duì)狀態(tài)XA;

步驟 4" 不施加軌道機(jī)動(dòng)，將飛行器軌道外推至瞄準(zhǔn)點(diǎn)所在圈次的緯度幅角，記錄時(shí)刻為tu，計(jì)算飛行器相對(duì)參考軌道的相對(duì)狀態(tài)X0c;

步驟 5" 根據(jù)瞄準(zhǔn)點(diǎn)相對(duì)狀態(tài)和飛行器自由飛行后相對(duì)狀態(tài)，得到初始控制誤差δX0=X0c-XA;

步驟 6" 根據(jù)δXk－1按照面內(nèi)三切向脈沖［24］求解近圓偏差方程，得到各次變軌位置和變軌脈沖;

步驟 7" 計(jì)算得到變軌策略后，施加軌道機(jī)動(dòng)，并外推得到終點(diǎn)時(shí)刻相對(duì)參考軌道的相對(duì)狀態(tài)Xkc，得到控制偏差δXk=Xkc-XA;

步驟 8" 判斷δXk是否滿(mǎn)足誤差要求，滿(mǎn)足則推出，不滿(mǎn)足轉(zhuǎn)步驟6;

步驟 9" 令δXk=δXk－1+δXk，轉(zhuǎn)步驟4（并令k=k+1）。

3" 仿真驗(yàn)證

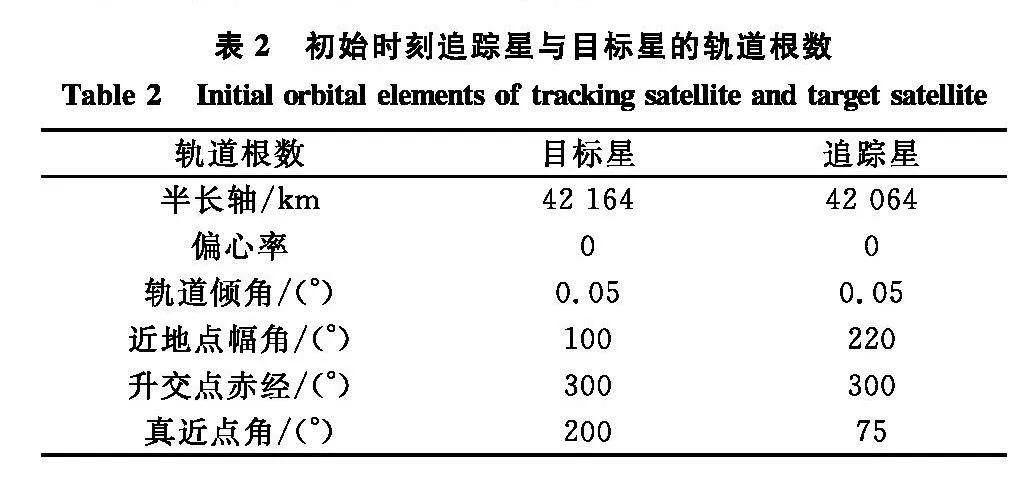
初始時(shí)刻追蹤星與目標(biāo)星的軌道根數(shù)如表2所示。軌道動(dòng)力學(xué)采用 20×20階地球非球形攝動(dòng)模型并考慮太陽(yáng)和月球引力攝動(dòng)，軌道控制采用脈沖方式施加［23］。

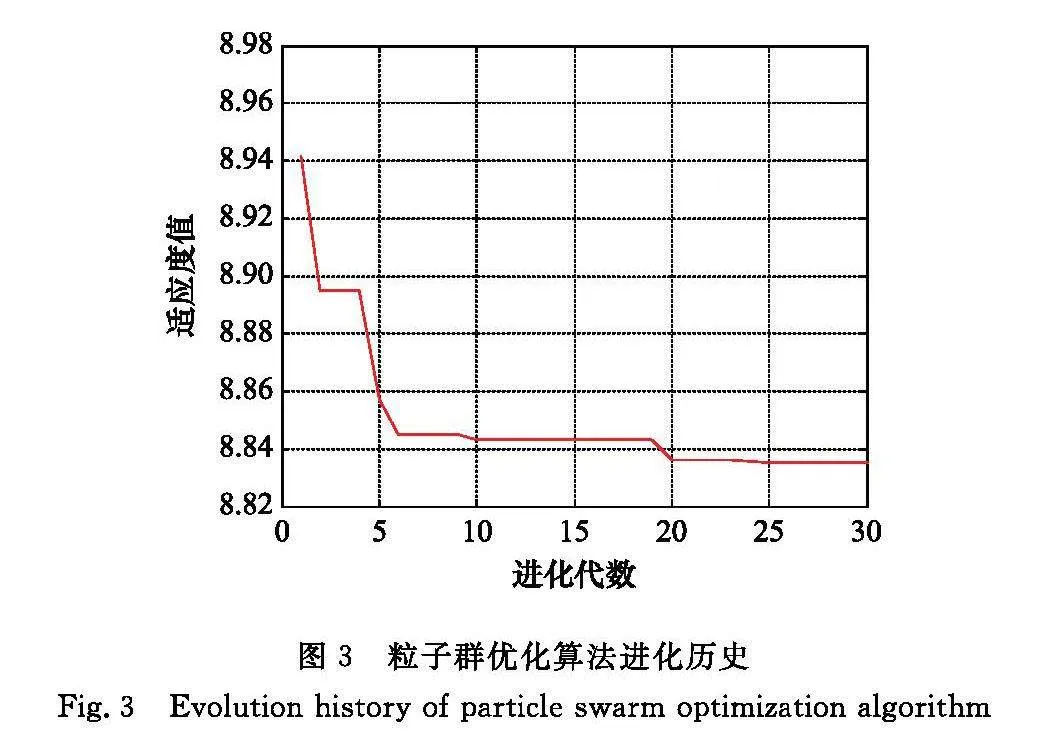
約束條件設(shè)置為任務(wù)時(shí)間不大于3天，接近最近距離不小于100 km，太陽(yáng)光照角不大于60°。采用前文設(shè)置的粒子群優(yōu)化參數(shù)，優(yōu)化求解后得到的目標(biāo)函數(shù)進(jìn)化歷史如圖3所示。

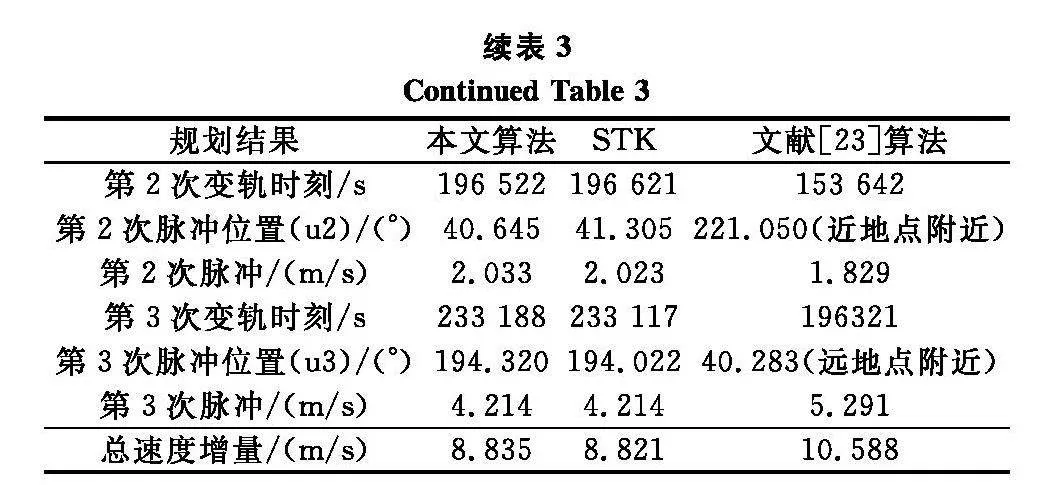
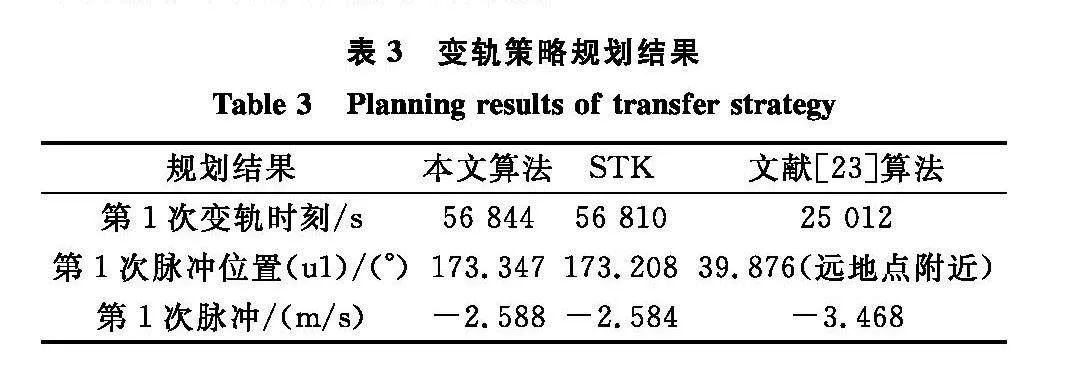
采用雙層優(yōu)化模型，得到了3次變軌位置和切向變軌速度增量大小，如表3所示。總變軌速度增量為8.835 m/s，與STK求解結(jié)果基本一致，驗(yàn)證了方法的正確性。采用文獻(xiàn)［23］算法規(guī)劃出的變軌策略，第1次變軌在遠(yuǎn)地點(diǎn)附近、第2次變軌在近地點(diǎn)附近，總變軌速度增量為10.588 m/s。可見(jiàn)，本文算法優(yōu)化得到總的速度增量?jī)?yōu)于文獻(xiàn)［23］，且變軌點(diǎn)不再受限于遠(yuǎn)近地點(diǎn)等特殊點(diǎn)。

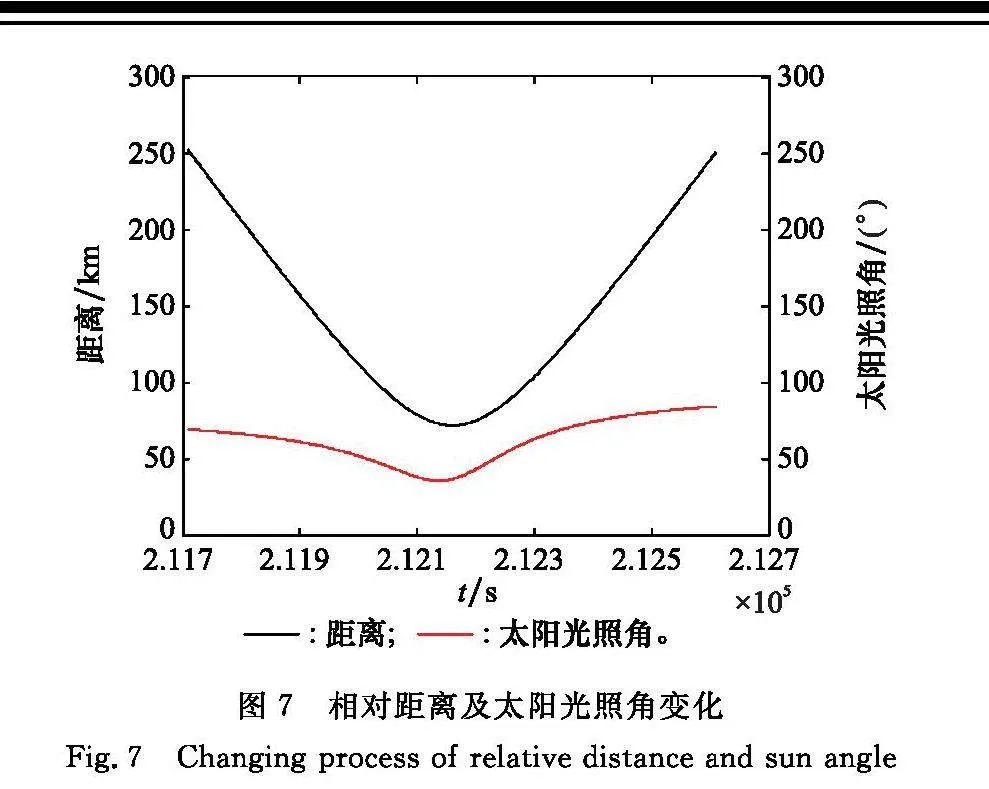
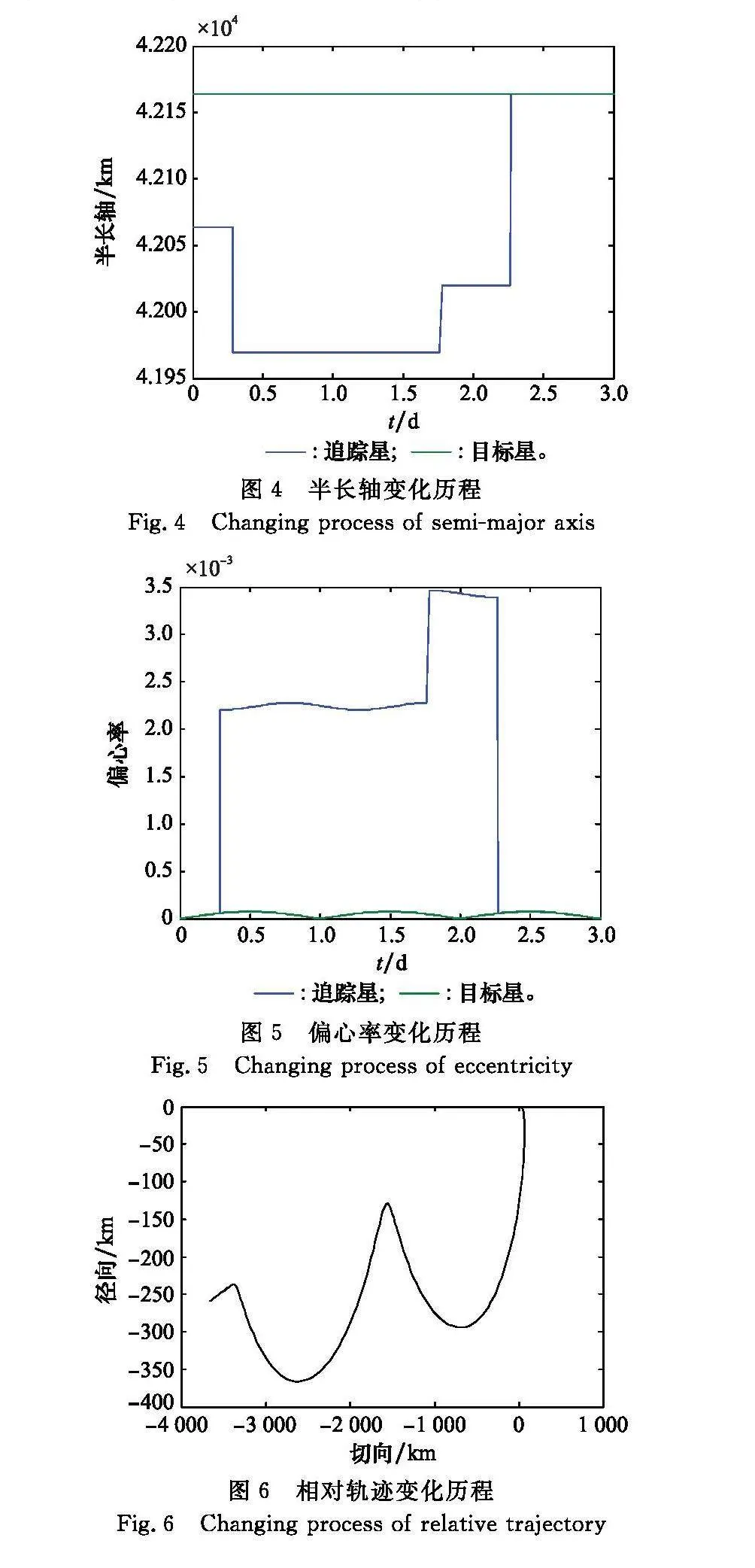
基于規(guī)劃的變軌策略開(kāi)展軌道仿真，得到主要軌道參數(shù)半長(zhǎng)軸、偏心率變化如圖4和圖5所示。變軌接近過(guò)程中面內(nèi)相對(duì)運(yùn)動(dòng)軌跡如圖6所示，交會(huì)過(guò)程中的相對(duì)距離和太陽(yáng)光照角變化如圖7所示，能同時(shí)滿(mǎn)足約束條件。

4" 結(jié)" 論

本文研究了高軌遠(yuǎn)程交會(huì)規(guī)劃問(wèn)題，提出了一種基于粒子群算法和近圓偏差線(xiàn)性方程的雙層規(guī)劃方法，通過(guò)三切向脈沖綜合變軌實(shí)現(xiàn)面內(nèi)調(diào)相接近。其中，外層采用粒子群優(yōu)化算法對(duì)兩次變軌的緯度幅角進(jìn)行尋優(yōu)，在確定前兩次脈沖位置后，內(nèi)層求解近圓偏差線(xiàn)性方程得到3次脈沖速度增量。突破了變軌在特殊點(diǎn)的限制，并減小了總速度增量，具有一定工程應(yīng)用意義。

參考文獻(xiàn)

［1］ SAMSAM S， CHHABRA R. Multi-impulse shape-based trajectory optimization for target chasing in on-orbit servicing missions［C］∥Proc.of the IEEE Aerospace Conference， 2021： 24112421.

［2］ ZHAO Y， CAO Y， CHEN Y， et al. Mission planning of GEO active debris removal based on revolver mode［J］. Mathematical Problems in Engineering： Theory， Methods and Applications， 2021， 2021： 8284022.

［3］ TARABINI L， GIL J， GANDIA F， et al. Ground guided CX-OLEV rendezvous with uncooperative geostationary satellite［J］. Acta Astronautica， 2007， 61（1/6）： 312325.

［4］ VERSTRAETE A W， ANDERSON D， LOUIS N M S， et al. Geosynchronous earth orbit robotic servicer mission design［J］. Journal of Spacecraft and Rockets， 2018， 55（6）： 14441452.

［5］ HAN P， GUO Y N， LI C T， et al. GEO satellites on-orbit repairing mission planning with mission deadline constraint using a large neighborhood search-genetic algorithm［EB/OL］. ［20230930］. https：∥arxiv.org/abs/2110.03878.

［6］ YU J， YU Y G， HAO D， et al. Biobjective mission planning for geosynchronous satellites on-orbit refueling［C］∥Proc.of the Institution of Mechanical Engineers， 2019： 686697.

［7］ 張進(jìn). 空間交會(huì)遠(yuǎn)程導(dǎo)引變軌任務(wù)規(guī)劃［D］. 長(zhǎng)沙： 國(guó)防科學(xué)技術(shù)大學(xué)， 2008.

ZHANG J. Phasing maneuver mission pre-flight planning for space rendezvous［D］. Changsha： National University of Defense Technology， 2008.

［8］ WANG J X， BAI H X， SUN L F. Optimal four-impulse rendezvous between coplanar elliptical orbits［J］. Science China （Phy-sics， Mechanics amp; Astronomy）， 2011， 54（4）： 792802.

［9］ TIAN X W， JIA Y M， CHEN C Q. Optimal four-impulse ellipse-to-ellipse coplanar rendezvous［C］∥Proc.of the IEEE 35th Chinese Control Conference， 2016： 54985503.

［10］ BARANOV A A， ROLDUGIN D S. Six-impulse maneuvers for rendezvous of spacecraft in near-circular noncoplanar orbits［J］. Cosmic Research， 2012， 50（6）： 441448.

［11］ PRUSSING J E， CHIU J H. Optimal multiple-impulse time-fixed rendezvous between circular orbits［J］. Journal of Guidance， Control amp; Dynamics， 2012， 9（1）： 7781.

［12］ BARANOV A A， GRISHKO D A， MEDVEDEVSKIKH V V， et al. Solution of the flyby problem for large space debris at sun-synchronous orbits［J］. Cosmic Research， 2016， 54（3）： 229236.

［13］ BARANOV A A， BUDYANSKY A A. Algorithm for calculation of the parameters of four maneuvers of a non-coplanar rendezvous in the vicinity of a circular orbit［J］. Cosmic Research， 2022， 60（6）： 491501.

［14］ SANTOS D P S D， ALMEIDA PRADO A F B D， COLASURDO G. Four-impulsive rendezvous maneuvers for spacecrafts in circular orbits using genetic algorithms［J］. Mathematical Problems in Engineering Theory， Methods and Applications， 2012， 2012： 94113.

［15］ 李蒙， 馬曉兵. 航天器遠(yuǎn)程自主交會(huì)方法設(shè)計(jì)與實(shí)現(xiàn)［J］. 宇航學(xué)報(bào)， 2017， 38（9）： 911918.

LI M， MA X B. Development of long distance autonomous rendezvous for spacecraft［J］. Journal of Astronautics， 2017， 38（9）： 911918.

［16］ 李革非， 宋軍， 劉成軍. 交會(huì)對(duì)接任務(wù)軌道控制規(guī)劃設(shè)計(jì)與實(shí)施［J］. 載人航天， 2014， 20（1）： 18.

LI G F， SONG J， LIU C J. Design and implementation of orbit maneuver programming in rendezvous and docking missions［J］. Manned Spaceflight， 2014， 20（1）： 18.

［17］ 李君龍， 李松洲， 周荻. 一種多約束條件下的三脈沖交會(huì)優(yōu)化設(shè)計(jì)方法［J］. 系統(tǒng)工程與電子技術(shù)， 2022， 44（8）： 26122620.

LI J L， LI S Z， ZHOU D. Optimization method for three impulse rendezvous under multi-constriants［J］. Systems Engineering and Electronics， 2022， 44（8）： 26122620.

［18］ BARBEE B W， CARPENTER J R， HEATWOLE， et al. A guidance and navigation strategy for rendezvous and proximity operations with a noncooperative spacecraft in geosynchronous orbit［J］. Journal of the Astronautical Sciences， 2011， 58（3）： 389408.

［19］ LUO Y Z， SUN Z J. Safe rendezvous scenario design for geostationary satellites with collocation constraints［J］. Astrodynamics， 2017， 1（1）： 7183.

［20］ LUO Y Z， SUN Z J， ZHANG J. Proximity scenario design for geostationary rendezvous with collocated satellite avoidance［J］. Acta Astronautica， 2019， 154： 153168.

［21］ 蔡亞星， 王興龍， 朱閱訸. GEO在軌服務(wù)任務(wù)建模與強(qiáng)化學(xué)習(xí)服務(wù)序列規(guī)劃［J］. 空間控制技術(shù)與應(yīng)用， 2022， 48（3）： 3948.

CAI Y X， WANG X L， ZHU Y H. On-orbit service mission modeling and reinforcement learning services sequence planning in GEO［J］. Aerospace Control and Application， 2022， 48（3）： 3948.

［22］ 王濤， 張鍇， 王新波， 等. GEO衛(wèi)星在軌服務(wù)路徑規(guī)劃方法［J］. 航天控制， 2022， 40（6）： 1116.

WANG T， ZHANG K， WANG X B， et al. A path planning method for GEO satellite on-orbit service［J］. Aerospace Control， 2022， 40（6）： 1116.

［23］ 劉濤， 胡海霞， 解永春. 靜止軌道衛(wèi)星遠(yuǎn)程交會(huì)策略設(shè)計(jì)［J］. 宇航學(xué)報(bào)， 2020， 41（8）： 10151022.

LIU T， HU H X， XIE Y C. Far-range rendezvous strategy planning for geostationary orbit satellites［J］. Journal of Astronautics， 2020， 41（8）： 10151022.

［24］ HUANG A Y， LUO Y Z， LI H N. Fast optimization of impulsive perturbed orbit rendezvous with finite iterations［EB/OL］. ［20230930］. https：∥arxiv.org/abs/2108.04759v1.

［25］ FUNKE Z K Z K. Long-duration proximity operations flexibly optimized for efficient inspection and servicing using free-orbit dyna-mics［D］. Cambridge： Massachusetts Institute of Technology， 2017.

［26］ GOODARZIMEHR V， OMIDINASAB F， TAGHIZADIEH N. Optimum design of space structures using hybrid particle swarm optimization and genetic algorithm［J］. World Journal of Engineering， 2023， 20（3）： 591608.

［27］ QIAN Y， XU M， ZENG Z F， et al. Optimal multiple-impulse time-fixed rendezvous using genetic algorithm［C］∥Proc.of the IEEE Information Engineering amp; Computer Science， 2010： 7781.

［28］ 李革非. 交會(huì)對(duì)接軌道控制規(guī)劃［M］. 北京： 國(guó)防工業(yè)出版社， 2016.

LI G F. Orbital control planning for rendezvous and docking［M］. Beijing： National Defence Industry Press， 2016.

［29］ 王濤， 徐巖. 粒子群優(yōu)化算法在配方設(shè)計(jì)中的應(yīng)用［J］. 微計(jì)算機(jī)信息， 2012， 28（1）： 178180.

WANG T， XU Y. The application of particle swarm optimization to cigarette design［J］. Microcomputer Information， 2012， 28（1）： 178180.

作者簡(jiǎn)介

徐廣德（1990—），男，高級(jí)工程師，博士，主要研究方向?yàn)轱w行器總體設(shè)計(jì)、任務(wù)規(guī)劃。

何晶晶（1996—），女，工程師，博士，主要研究方向?yàn)楣鈱W(xué)探測(cè)、計(jì)算機(jī)視覺(jué)。