適用于點群共存場景的TPMBM跟蹤算法

摘" 要：

針對傳統群目標跟蹤算法在點群共存場景下跟蹤精度低的問題，提出了可以同時對點目標和群目標進行跟蹤的軌跡泊松多伯努利混合（trajectory Poisson multi-Bernoulli mixture， TPMBM）濾波算法。該算法對目標的狀態空間進行擴展，在標準點目標和群目標模型的基礎上引入關于目標類別的概率信息，通過TPMBM濾波器的預測和更新過程實現對目標類別的判斷和對目標運動狀態的估計。仿真結果表明，與現有算法相比，所提算法在點目標和群目標共存時漏檢誤差明顯降低，具有更優的跟蹤性能。

關鍵詞：

目標跟蹤; 點群共存; 軌跡泊松多伯努利混合濾波

中圖分類號：

TN 953

文獻標志碼： A""" DOI：10.12305/j.issn.1001-506X.2024.07.04

TPMBM tracking algorithm suitable for point-group coexistence scenarios

ZHANG Shuangwu1， LI Cuiyun1，*， ZHAO Jingzhe2， HENG Bowen1

（1. School of Electronic Engineering， Xidian University， Xi’an 710071， China;

2. The 27th Research Institute of China Electronics Technology Group Corporation， Zhengzhou 450047， China）

Abstract：

In order to solve the problem of low tracking accuracy of the traditional group target tracking algorithms in point-group coexistence scenarios， a trajectory Poisson multi-Bernoulli mixture （TPMBM） filte-ring algorithm is proposed， which can track both point target and group target simultaneously. The algorithm expands the state space of the target， introduces probability information about the target class based on the standard point target and the group target models， and achieves the judgment of the target class and the estimation of the target motion state through the prediction and update process of the TPMBM filter. Simulation results show that， compared with the existing algorithms， the proposed algorithm has significantly lower miss detection error and better tracking performance when point target and group target coexist.

Keywords：

target tracking; point-group coexistence; trajectory Poisson multi-Bernoulli mixture （TPMBM） filtering

0" 引" 言

目標跟蹤指根據傳感器獲得的量測信息，通過跟蹤算法對當前時刻觀測區域內目標的數量和運動狀態做出估計的過程［14］。目標跟蹤廣泛應用于軍事和民用領域［5］，如艦艇探測、智駕［67］、智能機器人［89］等。當目標密集分布時，各個目標所產生量測的距離小于所設閾值，難以區分其來源，導致對目標的估計精度急劇下降。因此，通常將一組距離相近、運動模式相似的點目標視為一個整體，也就是一個群目標來進行跟蹤。對于群目標跟蹤問題，一般先使用量測劃分算法［10］得到量測可能的分組，再使用Murty 算法［11］選取若干個最優的量測分組方案。近年來，基于隨機有限集［12］（random finite set， RFS）的群目標跟蹤算法快速發展。其中，軌跡泊松多伯努利混合（trajectory Poisson multi-Bernoulli mixture， TPMBM）濾波算法［1315］將未檢測目標表示為泊松點過程（Poisson point process， PPP），將已檢測目標表示為多伯努利混合（multi-Bernoulli mixture，MBM）形式，以較高精度對目標當前運動狀態進行跟蹤的同時，還能保留目標的軌跡信息，是目前的研究熱點。

在群目標跟蹤問題中，群目標的外形建模方法非常重要，長期以來受到學者們的廣泛關注。Koch提出的隨機矩陣（random matrices， RM）法［16］是最為常用的群目標建模方法。Baum團隊使用曲線擬合技術實現群目標的外形建模，提出了適用于星凸形狀的隨機超曲面模型［17］和基于期望最大化（expectation maximization， EM）算法的隨機超曲面模型［18］。Yang等利用計算機圖形學中的 B樣條（B-splines， BS）和概率假設密度（probability hypothesis density， PHD）濾波器，提出了可用于跟蹤星凸群目標的 BS-PHD濾波器［19］。李翠蕓等在泊松MBM （Poisson MBM， PMBM）濾波器的基礎上使用 BS和移動最小二乘（moving least-squares， MLS）對目標外形建模，實現了較好的估計效果［2021］。基于箱粒子濾波，宋驪平等提出了一系列群目標跟蹤算法［2223］。

經過專家學者的大量研究，現有的多目標跟蹤算法已經可以對各種單一類別的目標進行準確跟蹤［2426］。群目標跟蹤算法由擴展目標算法發展而來，盡管在理論上存在很多相似性，但群成員相對位置的靈活性給跟蹤帶來了新的問題。事實上，點目標和群目標共存的情況是相當常見的，而現有的群目標跟蹤算法雖然對密集點目標有較高的估計精度，卻非常容易將來自稀疏點目標的量測當作背景噪聲，從而產生大量目標漏檢。由于針對這兩類目標的處理方式大不相同，在跟蹤過程中獲得目標的類別可以極大提高目標跟蹤算法的實用價值。因此，研究適用于點目標和群目標共存場景下的多目標跟蹤算法是十分重要的。目前，針對這一問題的研究不多。2021年，ngel等人率先取得進展，提出了同時包括點目標和擴展目標的廣義量測模型和單目標空間，并基于數據關聯的概率信息，推導了傳播點目標高斯密度和擴展目標伽馬高斯逆威舍特（Gamma Gaussian inverse Wishart， GGIW）密度的PMBM濾波遞歸［27］，為群目標跟蹤算法指引了新的發展方向。雖然PMBM以精確的封閉形式解決了未標記的多目標貝葉斯濾波器［28］。然而，PMBM濾波器無法提供時間步長之間的目標軌跡［29］，并且該文獻并未考慮目標類別發生轉換的場景。

針對上述問題，本文提出了一種適用于點群共存場景的TPMBM多目標跟蹤算法。算法基于點目標模型和群目標模型對目標的狀態空間進行擴展，給出了點群（point group， PG）共存場景下的目標描述方法;然后將該目標描述方法與GGIW-TPMBM濾波算法相結合，提出了可以同時對點目標和群目標進行跟蹤的PG-GGIW-TPMBM濾波算法。仿真實驗結果表明，所提算法可以實現點群共存場景下對目標類別的判斷和軌跡狀態的跟蹤。

1" 點群共存模型

1.1" 點目標模型和群目標模型

在標準點目標量測模型中，x表示一個點目標，假設目標被檢測到的概率是pD（x），如果被檢測到，該目標產生一個概率密度為l（·|x）的量測，則該模型［30］可以描述為

f（Z|x）=1－pD（x），Z=

pD（x）l（z|x），Z={z}

0，|Z|gt;1（1）

對于一個點目標，如果對應的量測集Z為空，說明該目標未被檢測到。由于點目標最多生成一個量測，因此|Z|gt;1的情況不可能發生。

在標準的群目標模型中，x表示一個群目標，假設目標被檢測到的概率是pD（x），如果被檢測到，該目標以γ（x）·l（·|x）的密度生成PPP形式的量測，其中l（z|x）表示單個量測的概率密度，γ（x）表示量測數量的期望。該模型可以描述為

f（Z|x）=1－pD（x）+pD（x）e－γ（x），Z=

pD（x）γ|Z|（x）e－γ（x）∏z∈Zl（z|x），|Z|gt;0（2）

對于一個群目標，如果對應的量測集Z為空，說明該目標未被檢測到，或者目標被檢測到但未生成量測。

1.2" 點群共存場景下的目標描述方法

由第1.1節可以看出，點目標和群目標的模型存在很大差異。如果要實現點群共存場景下的目標跟蹤，首先要構建同時容納點目標和群目標的狀態空間。對于一個點目標，將其運動狀態空間表示為Rnx。對于一個GGIW形式的群目標，其狀態空間可以表示為Xe=R+×Rnx×Sd+，其中R+表示正實數，Sd+表示d維正定矩陣，其中d為群目標外形的維度。對于一個群目標x，可以進一步表示為x=（γ，ξ，G）。其中，γ表示群目標的期望量測數，ξ表示群目標的運動狀態，G表示群目標的外形。在點群共存模型中，單目標狀態空間X可以表示為點目標和群目標狀態空間的不相交并集，即X=RnxXe。如果一個目標x∈Rnx，則f（Z|x）為式（1）中的形式，檢測概率pD（x）=pD1，l（·|x）=N（z;H1x，R）。其中，H1為點目標的觀測矩陣，R為噪聲協方差矩陣，N（·;x-，P）表示均值為x-，協方差為P的高斯分布。如果一個目標x∈Xe，則f（Z|x）為式（2）中的形式，檢測概率pD（x）=pD2，γ（x）=γ，l（·|x）=N（z;H2ξ，G），其中H2為群目標的觀測矩陣。

對于一個目標x∈X，如果其概率密度服從均值為x-i，ai，1k|k′，方差為Pi，ai，1k|k′的高斯分布，可以表示為

Np（x;x-i，ai，1k|k′，Pi，ai，1k|k′）=N（x;x-i，ai，1k|k′，Pi，ai，1k|k′）（3）

此時，x為點目標的概率為1，為群目標的概率為0。

對于一個目標x∈X，如果其概率密度服從GGIW分布，可以參數化表示如下：

ζi，aik|k′=（αi，aik|k′，βi，aik|k′，x-i，ai，2k|k′，Pi，ai，2k|k′，vi，aik|k′，Vi，aik|k′）（4）

Ge（x;ζi，aik|k′）=

G（γ;αi，aik|k′，βi，aik|k′）N（ξ;x-i，ai，2k|k′，Pi，ai，2k|k′）·IW（X;vi，aik|k′，Vi，aik|k′）（5）

此時，x為群目標的概率為1，為點目標的概率為0;G（γ;αi，aik|k′，βi，aik|k′）表示伽馬分布的概率密度函數，其中γgt;0，形狀參數αgt;0，逆尺度參數βgt;0;N（ξ;x-i，ai，2k|k′，Pi，ai，2k|k′）表示高斯分布的密度函數，x-i，ai，2k|k′和Pi，ai，2k|k′表示高斯分布的均值和方差;IW（X;vi，aik|k′，Vi，aik|k′）表示d維的逆威舍特分布，其中，自由度vgt;2d;V表示逆尺度矩陣;d為擴展狀態維數，二維場景下設置為2。逆威舍特分布用來表示群目標的整體外形。

基于上述思想，對于一個未知類別目標的伯努利項，可以將其概率密度函數表示為

fi，aik|k′（x）=

ci，aik|k′Np（x;x-i，ai，1k|k′，Pi，ai，1k|k′）+（1－ci，aik|k′）Ge（x;ζi，aik|k′）（6）

式中：ci，aik|k′和（1－ci，aik|k′）分別表示目標為點目標和群目標的概率;i表示伯努利項的索引;ai表示局部假設。

2" 基于點群共存模型的PG-GGIW-TPMBM跟蹤算法

基于第1.2節中的目標描述方法，可以得到適用于PG共存場景的GGIW-TPMBM（簡稱為PG-GGIW-TPMBM）濾波器。PG-GGIW-TPMBM濾波器假設點目標服從高斯分布，群目標服從GGIW分布，可以實現對點目標軌跡和群目標軌跡的同時跟蹤。對于點目標軌跡X，可以將其表示為Np（X;tpb，{x-pk，Ppk}）。其中，tpb表示點目標軌跡的新生時間，{x-pk，Ppk}表示新生時刻到k時刻的狀態序列集。對于群目標軌跡X，可以將其表示為Ge（X;teb，{ζek}）。其中，teb表示群目標軌跡的新生時間。傳統的GGIW-TPMBM只針對群目標進行預測更新，并沒有對所跟蹤的目標類別進行判斷，將所有目標全部考慮為群目標，其概率密度服從GGIW分布，參數表示為式（5）。與GGIW-TPMBM不同的是，在PG-GGIW-TPMBM的濾波過程中，通過引入點目標濾波算法，并利用類型概率ci，aik|k′來判斷目標類別。

與GGIW-TPMBM濾波器相同，PG-GGIW-TPMBM的濾波過程包括預測和更新兩部分，具體如下。

（1） PG-GGIW-TPMBM的預測過程

在點群共存模型中， PG-GGIW-TPMBM的預測包括對PPP部分的預測和對MBM部分的預測。

目標軌跡在k時刻的新生強度可以表示為

λBk（X）=∑nb，pkq=1wb，p，qkNp（X;k，{x-b，p，q，1k，Pb，p，q，1k}）+

∑nb，ekq=1wb，e，qkGe（X;k，{ζb，e，qk}） （7）

式中：nb，pk表示點目標軌跡項的數量;wb，p，qk表示點目標軌跡項的權重;nb，ek表示PPP中群目標軌跡項的數量;wb，e，qk表示群目標軌跡項的權重;∑nb，pkq=1wb，p，qk和∑nb，ekq=1wb，e，qk分別表示未檢測到的點目標軌跡和群目標軌跡的數量;Np（X;k，{x-b，p，q，1k，Pb，p，q，1k}）表示一條點目標軌跡，Ge（X;k，{ζb，e，qk}）表示一條群目標軌跡。由于PPP中的目標軌跡尚未被檢測到，其新生時間均視為當前時刻k，軌跡長度均為1。

目標軌跡在k－1時刻的PPP強度可以表示為

λk－1|k－1（X）=∑npk－1|k－1q=1wp，qk－1|k－1Np（X;k，{x-p，q，1k－1|k－1，Pp，q，1k－1|k－1}）+

∑nek－1|k－1q=1we，qk－1|k－1Ge（X;{ζe，qk－1|k－1}）（8）

經過預測步驟后，PPP部分表示如下：

λk|k－1（X）=∑npk－1|k－1q=1pSwp，qk－1|k－1Np（X;k，{x-p，q，1k|k－1，Pp，q，1k|k－1}）+

∑nek－1|k－1q=1pSwe，qk－1|k－1Ge（X;k，{ζe，qk|k－1}）+λBk（X）（9）

式中：

（x-p，q，1k|k－1，Pp，q，1k|k－1）=pp（x-p，q，1k－1|k－1，Pp，q，1k－1|k－1） （10）

ζe，qk|k－1=pe（ζe，qk－1|k－1）（11）

式中：pp和pe分別表示卡爾曼濾波和GGIW的預測過程。

為了描述方便，將式（6）中的單目標概率密度進一步表示為

fi，aik|k′（x）=Hp，e（x;ci，aik|k′，x-i，ai，1k|k′，Pi，ai，1k|k′，ζi，aik|k′）（12）

假設k－1時刻第i個伯努利項在局部假設ai下的單軌跡密度為

fi，aik－1|k－1（X）=Hp，e（X;t，{ci，aik－1|k－1，x-i，ai，1k－1|k－1，Pi，ai，1k－1|k－1，ζi，aik－1|k－1}）（13）

對于 MBM部分來說，對軌跡X的預測意味著對其最后一個目標狀態ζend進行預測得到ζend+，并將ζend+添加到X的狀態序列中，即{ζj，i+}={{ζj，i}，ζend+}。

經過預測步驟后，該伯努利項的單軌跡密度為

fi，aik|k－1（X）=Hp，e（X;t，{ci，aik|k－1，x-i，ai，1k|k－1，Pi，ai，1k|k－1，ζi，aik|k－1}）（14）

式中：

（x-i，ai，1k|k－1，Pi，ai，1k|k－1）=pp（x-i，ai，1k－1|k－1，Pi，ai，1k－1|k－1） （15）

ζi，aik|k－1=pe（ζi，aik－1|k－1） （16）

ci，aik|k－1=ci，aik－1|k－1（17）

（2） PG-GGIW-TPMBM的更新過程

對于單個點目標軌跡，將均值為x-i，ai，1k|k－1，協方差為Pi，ai，1k|k－1的高斯密度在給定量測z下的卡爾曼更新表示為

（x-i，ai，1k|k，Pi，ai，1k|k，i，ai，1k|k）=up（x-i，ai，1k|k－1，Pi，ai，1k|k－1，z）（18）

式中：x-i，ai，1k|k表示軌跡中目標狀態更新后的均值;Pi，ai，1k|k表示軌跡中目標狀態更新后的協方差;i，ai，1k|k表示似然函數。

對于單個群目標軌跡，將參數為ζi，aik|k－1的GGIW項在給定量測集Zjk下的更新表示為

（ζe，qk|k，e，qk|k）=ue（ζi，aik|k－1，Zjk）（19）

式中：ζe，qk|k為GGIW項更新后的參數;e，qk|k為似然函數。

對于PPP部分中的點目標軌跡：

npk|k=npk|k－1（20）

x-p，q，1k|k=x-p，q，1k|k－1（21）

Pp，q，1k|k=Pp，q，1k|k－1（22）

wp，qk|k=（1－pD1）wp，qk|k－1（23）

對于PPP中的群目標軌跡：

nek|k=2nek|k－1（24）

如果q≤nek|k－1，說明對應的GGIW項未被檢測到，繼續在PPP中參與后續濾波：

ζe，qk|k=ζe，qk|k－1（25）

we，qk|k=（1－pD2）we，qk|k－1（26）

如果qgt;nek|k－1，q～=q－nek|k－1，說明該GGIW項被檢測到，但未匹配到量測，繼續在PPP中參與后續濾波：

（ζe，qk|k，e，qk|k）=ue（ζe，q～k|k－1，） （27）

（ζe，qk|k，e，qk|k）=ue（ζe，q～k|k－1，）we，qk|k=pD2e，qk|kwe，q～k|k（28）

we，qk|k=pD2e，qk|kwe，q～k|k（29）

對于MBM部分中已存在的伯努利項，如果發生漏檢，對應軌跡的概率密度函數為

fi，aik|k（X）=Hp，e（X;t，{ci，aik|k，x-i，ai，1k|k，Pi，ai，1k|k，ζi，ai，2k|k}）（30）

式中：

x-i，ai，1k|k=x-i，ai，1k|k－1（31）

Pi，ai，1k|k=Pi，ai，1k|k－1（32）

ζi，ai，1k|k=ζi，aik|k－1（33）

（ζi，ai，2k|k，i，ai，2k|k）=ue（ζi，aik|k－1，）（34）

li，ai，k|k=

ci，aik|k－1（1－pD1）+（1－ci，aik|k－1）（1－pD2+pD2i，ai，2k|k） （35）

wi，aik|k=wi，aik|k－1［1－ri，aik|k－1+ri，aik|k－1li，ai，k|k］ri，aik|k（36）

ri，aik|k=ri，aik|k－1li，ai，k|k1－ri，aik|k－1+ri，aik|k－1li，ai，k|k（37）

ci，aik|k=（1－pD1）ci，aik|k－1li，ai，k|k（38）

w=1－pD21－pD2+pD2i，ai，2k|k（39）

對于MBM部分中已存在的伯努利項，如果存在關聯的量測單元Zjk且|Zjk|=mjk，說明該軌跡假設被檢測到：

（ζi，aik|k，i，aik|k）=ue（ζi，a～ik|k－1，Zjk） （40）

ri，aik|k=1（41）

wi，aik|k=wi，a～ik|k－1ri，a～ik|k－1li，ai，Zjkk|k（42）

如果mjkgt;1，說明該目標同時匹配到多個量測，認為其一定是群目標：

li，ai，Zjkk|k=pD2i，aik|k（43）

ci，aik|k=0（44）

如果mjk=1，Zjk={z}，說明該目標只匹配到一個量測，則其既有可能是點目標，也有可能為群目標：

（x-i，ai，1k|k，Pi，ai，1k|k，i，ai，1k|k）=up（x-i，ai，1k|k－1，Pi，ai，1k|k－1，z） （45）

li，ai，Zjkk|k=ci，aik|k－1pD1i，ai，1k|k+（1－ci，aik|k－1）pD2i，aik|k（46）

ci，aik|k=ci，aik|k－1pD1i，ai，1k|kli，ai，Zjkk|k（47）

對于與Zjk關聯的新生伯努利項：

fi，2k|k（X）=Hp，e（X;t，{ci，2k|k，x-i，2，qk|k，Pi，2，qk|k，ζi，2，qk|k}） （48）

（ζi，2，qk|k，i，2，q2，k|k）=ue（ζe，qk|k－1，Zjk） （49）

wi，2k|k=δ1［|Zjk|］∏z∈ZjkλC（z）+lZjkk|k（50）

如果mjkgt;1，那么該目標一定為群目標：

lZjkk|k=pD2∑nek|k－1q=1we，qk|k－1i，2，q2，k|k（51）

ri，2k|k=1（52）

ci，2k|k=0（53）

如果mjk=1，Zjk={z}，那么該目標既有可能為點目標，也有可能為群目標：

（x-i，2，qk|k，Pi，2，qk|k，i，2，q1，k|k）=up（x-p，q，1k|k－1，Pp，q，1k|k－1，z） （54）

lZjkk|k=pD1∑npk|k－1q=1wp，qk|k－1i，2，q1，k|k+pD2∑nek|k－1q=1we，qk|k－1i，2，q2，k|k（55）

ri，2k|k=lZjkk|kwi，aik|k（56）

ci，2k|k=pD1∑npk|k－1q=1wp，qk|k－1i，2，q1，k|klZjkk|k（57）

完成預測和更新步驟后，通過ci，aik|k的取值判斷軌跡中目標的類別，如果ci，aik|kgt;0.5，認為該目標為點目標，運動狀態為x-i，ai，1k|k。如果ci，aik|k≤0.5，則認為該目標為群目標，軌跡中目標狀態序列的量測率、運動狀態和整體外形分別為

γ^=－αj，iklnβj，ikβj，ik+1αj，ik（58）

ξ^k={x-i，ai，2k|k}（59）

G^k=Vi，aik|kvi，aik|k－2d－2（60）

3" 仿真實驗與分析

為了驗證第2節中提出的PG-GGIW-TPMBM濾波器對不同類別目標的跟蹤能力，本節通過實驗對比了GGIW-TPMBM和PG-GGIW-TPMBM濾波器在不同場景下的估計精度。本節共包含3個實驗，實驗1主要檢驗PG-GGIW-TPMBM濾波器在群目標場景下的跟蹤性能;實驗2主要檢驗PG-GGIW-TPMBM濾波器在點目標和群目標共存場景下的跟蹤性能;實驗3主要檢驗PG-GGIW-TPMBM濾波器在目標類別轉換場景下的跟蹤性能。在本節中，所有實驗均采用廣義最優子模式分配（generalized optimal subpattern assignment， GOSPA）距離誤差［31］作為評價指標，且取100次蒙特卡羅實驗的平均值。GOSPA實際上是OSPA的非歸一化表現形式，其定義為

d（c，2）p（X，Y）=

minγ∈Γ∑（i，j）∈γd（xi，yj）p+

cp2（|X|－|γ|1+|Y|－|γ|1）1p（61）

GOSPA同時考慮了目標的定位誤差、漏檢誤差和虛警誤差。其中，p是自由度，c是截斷距離，X表示真實目標集合，Y表示估計的目標集合，Γ表示所有可能分配的集合，γ表示其中一種分配情況，d（xi，yj）表示真實目標和估計目標的歐氏距離，本文單位為m，|X|－|γ|表示漏檢的目標數量，|Y|－|γ|表示虛警的目標數量。

實驗 1" 為了驗證PG-GGIW-TPMBM濾波器對群目標的識別與跟蹤能力，設計如下模擬場景。傳感器的可視范圍為［－400，400］m×［－400，400］m，獲得的量測中包含二維笛卡爾坐標系下的位置信息。實驗過程中一共生成3個群目標，其運動模型為勻速直線運動模型，設目標的狀態轉移矩陣和觀測矩陣分別為F和H，過程協方差矩陣為Q，量測噪聲協方差為R，具體參數如下：

F=I2TI2

02I2H=［I2" 02］（62）

Q=σ2ωT33I2T22I2

T22I2TI2R=σ2v［I2］（63）

式中：T=1 s，表示傳感器采樣的時間間隔;σω=1 m/s2;σv=0.4 m。實驗中，目標軌跡的存活概率ps=0.99，傳感器對每個目標軌跡的檢測概率pD=0.90，背景噪聲的泊松率為8，GOSPA距離誤差的參數c=10，p=2。群目標外形服從參數為v=20，V=diag［200，200］的GGIW分布，量測率為10。表1給出了各個群目標的初始狀態和存活時間。目標狀態表示為［x，y，vx，vy］T，其中［x，y］T表示目標位置信息，單位為m；［vx，vy］T表示目標在x和y方向上的速度，單位為m/s。

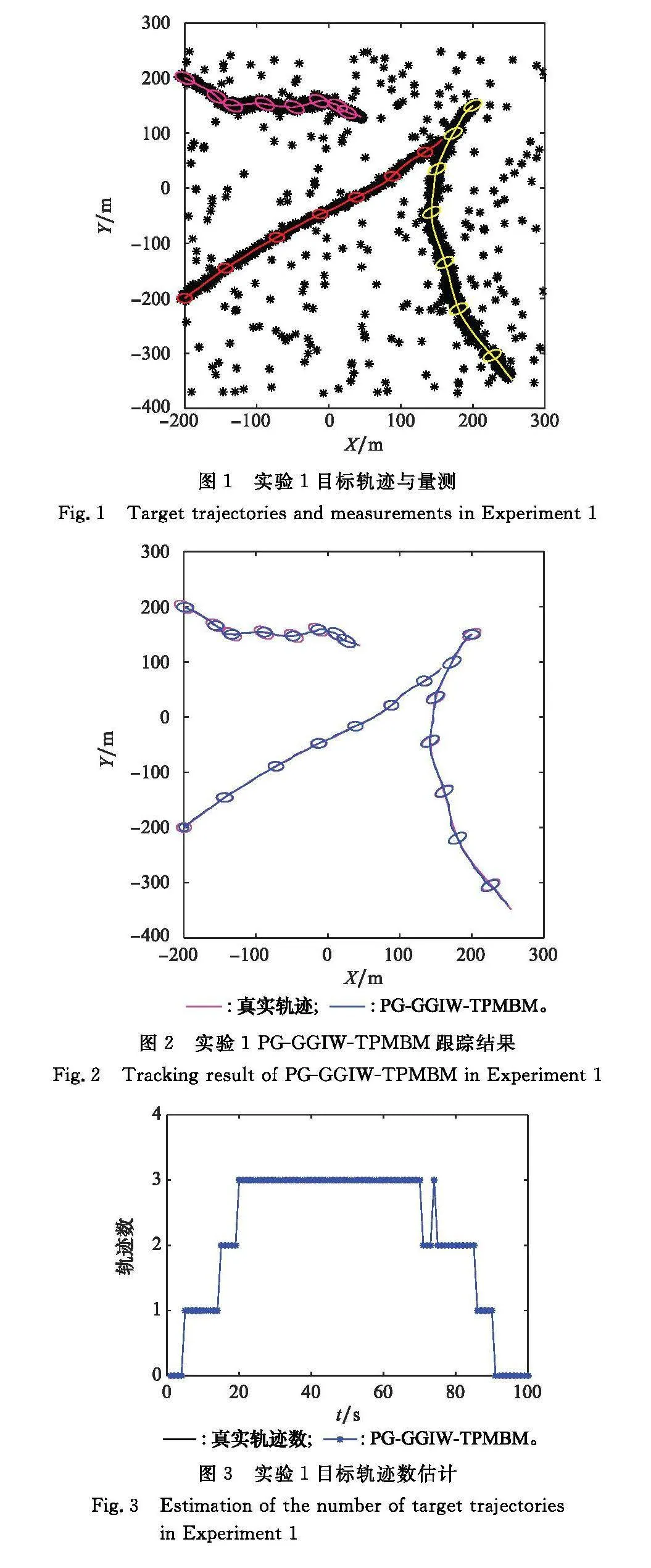
圖1為3個群目標的運動軌跡和傳感器接收到的量測，其中不同顏色的線條表示不同群目標的軌跡，每10個時刻標記一次群目標外形。黑色“*”表示目標量測和背景噪聲。PG-GGIW-TPMBM對3個群目標軌跡的跟蹤結果如圖2所示，圖3為跟蹤過程中PG-GGIW-TPMBM估計出的目標軌跡數量，圖4給出了跟蹤過程中的各項GOSPA距離誤差，包括總誤差、定位誤差、虛警誤差和漏檢誤差。

從圖2～圖4可以看出，算法能夠比較準確的估計群目標的質心位置和軌跡數量。在整個跟蹤過程中，PG-GGIW-TPMBM的定位誤差始終保持在較低水平，對軌跡數量的估計在第74個時刻出現了虛警，隨著后續時刻該軌跡假設沒有相匹配的量測，對應伯努利項的存在概率下降至存在閾值以下，導致該伯努利項被剪枝，虛警現象迅速得到糾正，這充分體現出算法的多假設結構所帶來的優勢。此外，PG-GGIW-TPMBM對群目標的類別判斷完全正確，表明其可以對群目標進行有效識別。上述實驗表明，所提算法在群目標場景下具有良好的識別與跟蹤能力。

實驗 2" 為了驗證PG-GGIW-TPMBM濾波器相較于GGIW-TPMBM濾波器在點群共存場景下對各類目標的識別與跟蹤能力，設計如下模擬場景。傳感器的可視范圍為［－400，400］m×［－400，400］m，獲得的量測中包含二維笛卡爾坐標系下的位置信息。實驗過程中一共生成5個目標，包括3個群目標和2個點目標，各個目標的初始狀態和存活時間如表2所示。所有目標的運動模式與實驗一相同，群目標外形服從參數為v=20，V=diag［200，200］的GGIW分布，量測率為10，背景噪聲的泊松率為8。GOSPA距離誤差的參數為c=10，p=2。PG-GGIW-TPMBM濾波器的各項參數與實驗1相同。

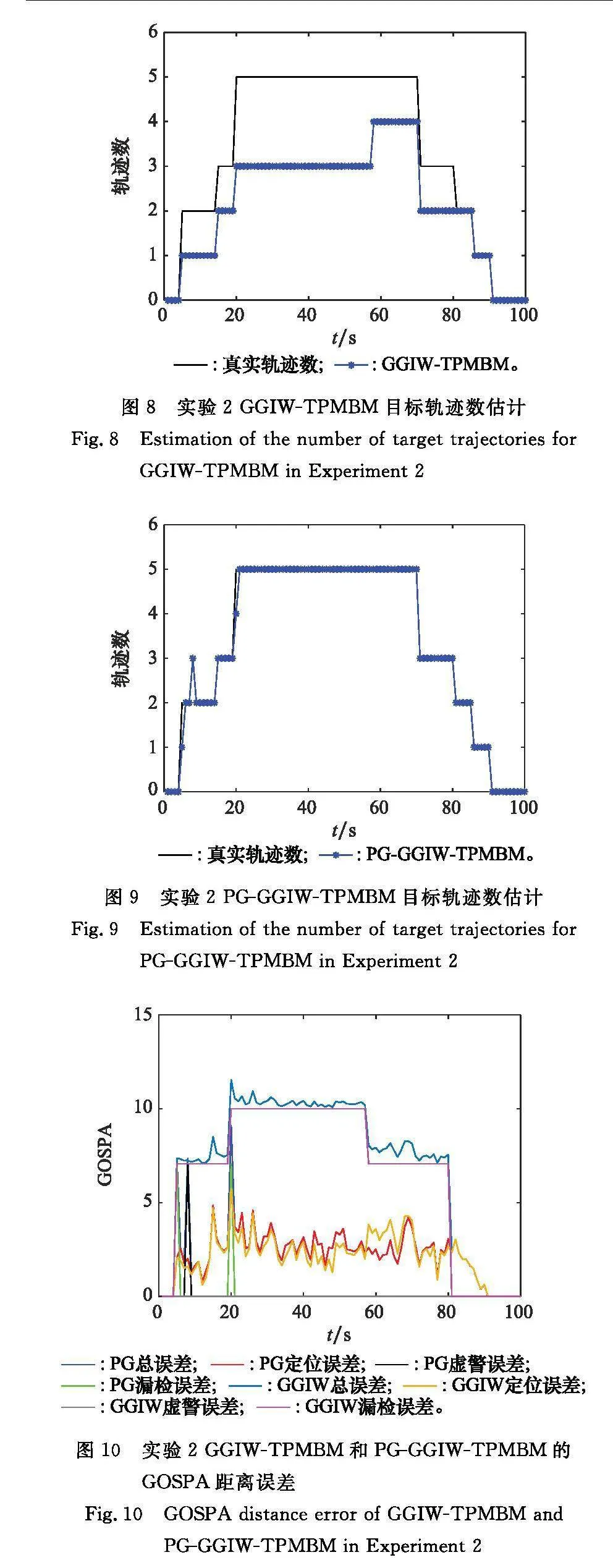
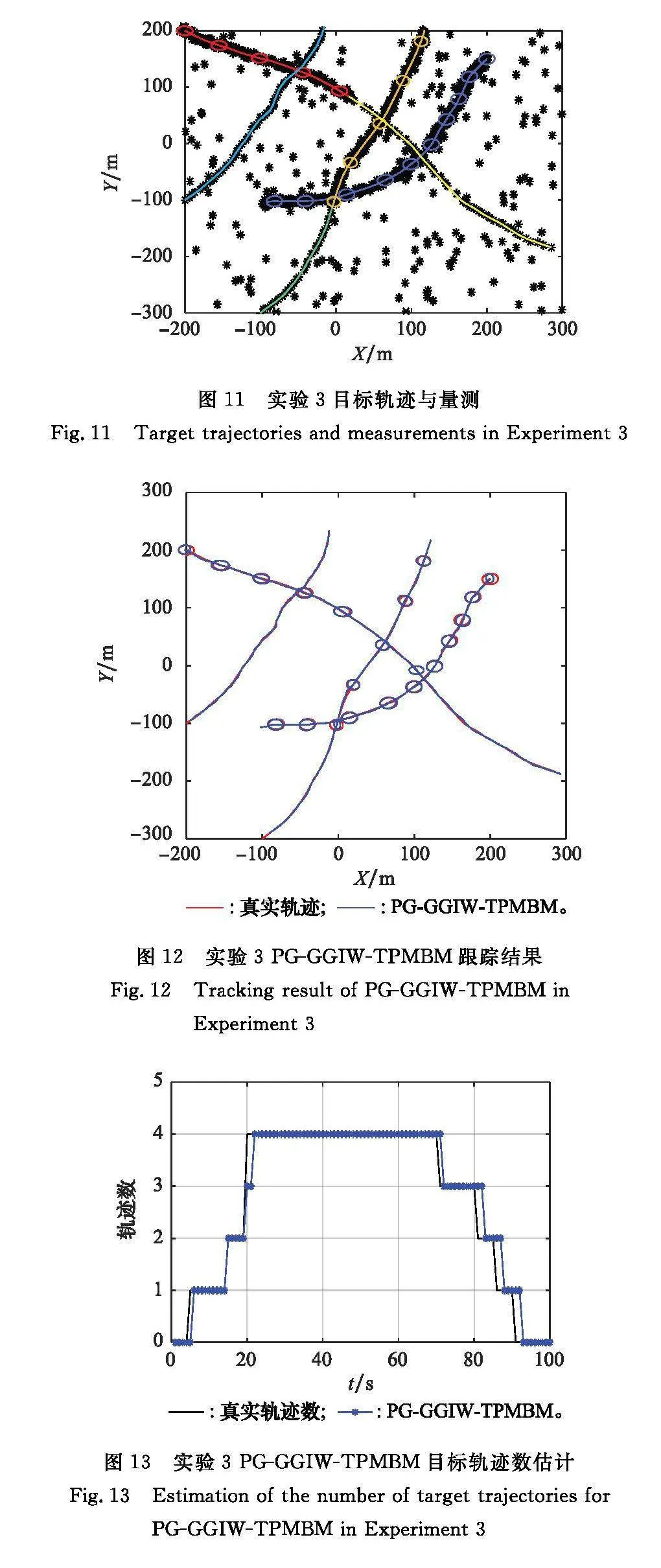
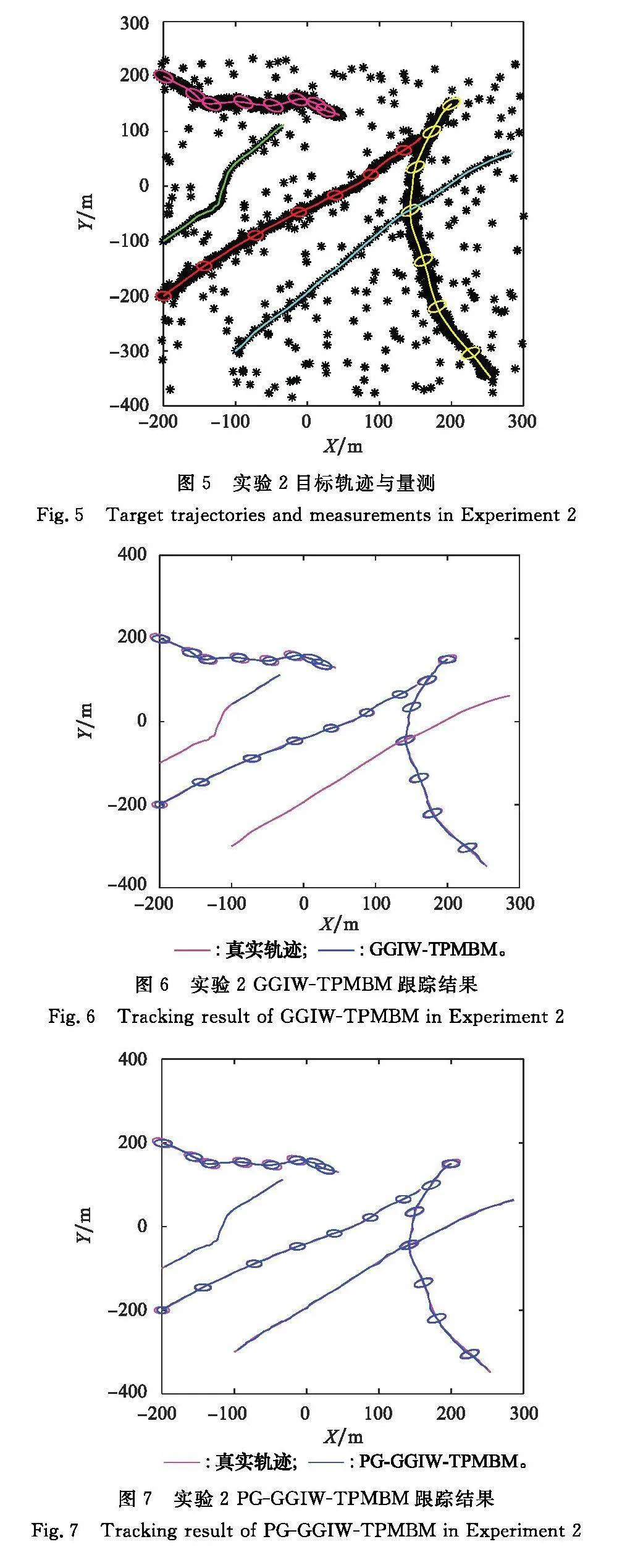
圖5給出了各個目標的運動軌跡和傳感器接收到的量測，其中不同顏色的線條表示不同目標的軌跡，每10個時刻標記一次群目標的外形，黑色“*”表示傳感器接收到的目標量測和背景噪聲。圖6和圖7分別給出了GGIW-TPMBM和PG-GGIW-TPMBM對點群共存目標的跟蹤結果，圖8和圖9分別給出了兩算法對目標軌跡數量的估計結果，圖10給出了兩算法在跟蹤過程中的各項GOSPA距離誤差。

GGIW-TPMBM in Experiment 2

PG-GGIW-TPMBM in Experiment 2

GOSPA距離誤差

PG-GGIW-TPMBM in Experiment 2

從圖6和圖7可以看出，在點群目標共存場景下，GGIW-TPMBM和PG-GGIW-TPMBM對于群目標質心和整體外形都能夠有效跟蹤，且精度相差不大。然而，GGIW-TPMBM無法區分目標類別，而是將所有目標都建模為群目標，而PG-GGIW-TPMBM基于第1節中提出的點群共存目標描述方法，對于目標類別的判斷完全正確。從圖8可以看出，在跟蹤過程中，GGIW-TPMBM出現了嚴重的目標軌跡漏檢現象，結合圖6可知漏檢主要發生在對點目標的跟蹤中，這是因為GGIW-TPMBM將點目標視為只包含一個成員的特殊群目標，而點目標每個時刻只生成一個量測。由文獻［4］可知，PPP部分中單個軌跡假設關聯到量測集C時所生成的伯努利項的存在概率為

ruC=1， |C|gt;1

CκC+C， |C|=1（64）

當量測單元中包含多個量測時，生成的伯努利項存在概率始終為1，這使得GGIW-TPMBM能夠比較準確地捕捉到新生群目標;當量測單元中只包含一個量測時，生成的伯努利項存在概率變小，且與雜波率有關。雜波率越大，伯努利項的存在概率越小，越容易被剪枝，從而導致GGIW-TPMBM對于點目標的頻繁漏檢。

從圖9可以看出，PG-GGIW-TPMBM對于軌跡數量的估計精度較高，盡管在第5、20個時刻發生了漏檢，在第8個時刻發生了虛警，但都能夠利用量測數據及時修正，這主要是因為PG-GGIW-TPMBM對目標的狀態空間進行了改進。當單個軌跡假設只匹配到一個量測時，充分考慮到該目標為點目標的可能性，并將點目標的狀態估計加入濾波過程，從而提高了PG-GGIW-TPMBM對點目標的識別與跟蹤能力。從圖10可以看出，在點群共存場景下，兩算法的定位誤差相差不大，但PG-GGIW-TPMBM在漏檢誤差方面具有突出優勢。通過上述實驗，充分驗證了所提算法同時對點目標和群目標進行跟蹤時的良好性能。

實驗 3" 為了驗證PG-GGIW-TPMBM濾波器在目標類別轉換的場景下對各類目標的識別與跟蹤能力，設計如下模擬場景。傳感器的可視范圍為［－400，400］m×［－400，400］m，獲得的量測中包含二維笛卡爾坐標系下的位置信息。實驗過程中一共生成4個目標，各個目標的初始狀態和存活時間如表3所示，其中群目標1在46時刻變為點目標;點目標4在50時刻變為群目標。所有目標的運動模式與實驗1相同，群目標外形服從參數為v=20，V=diag［200，200］的GGIW分布，量測率為10，背景噪聲的泊松率為8。GOSPA距離誤差的參數為c=10，p=2。PG-GGIW-TPMBM濾波器的各項參數與實驗1相同。

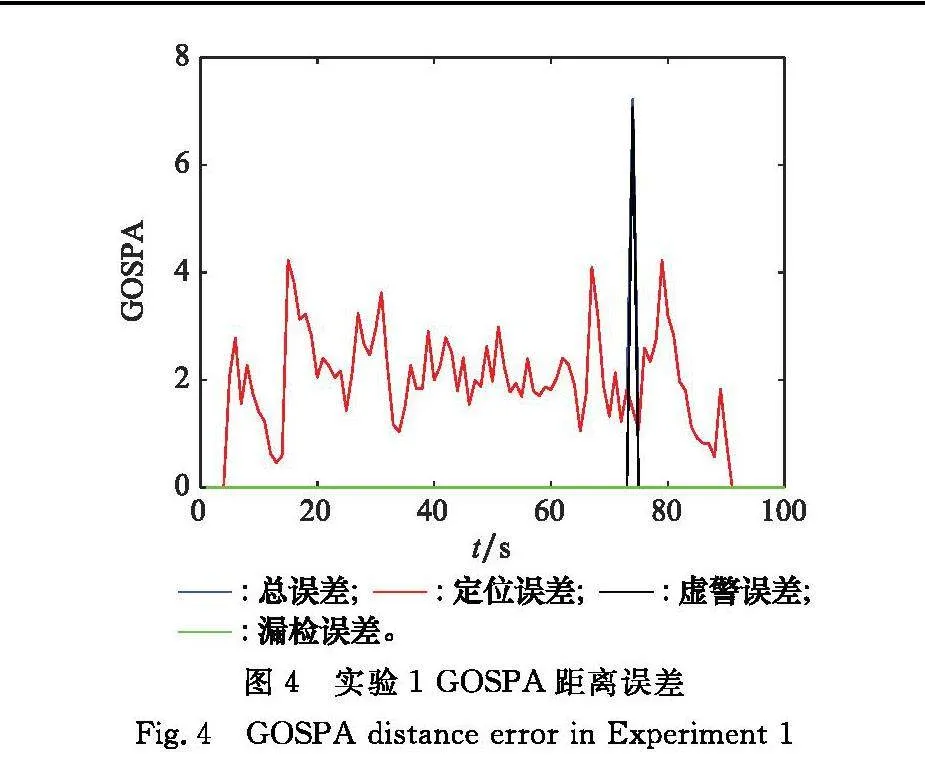
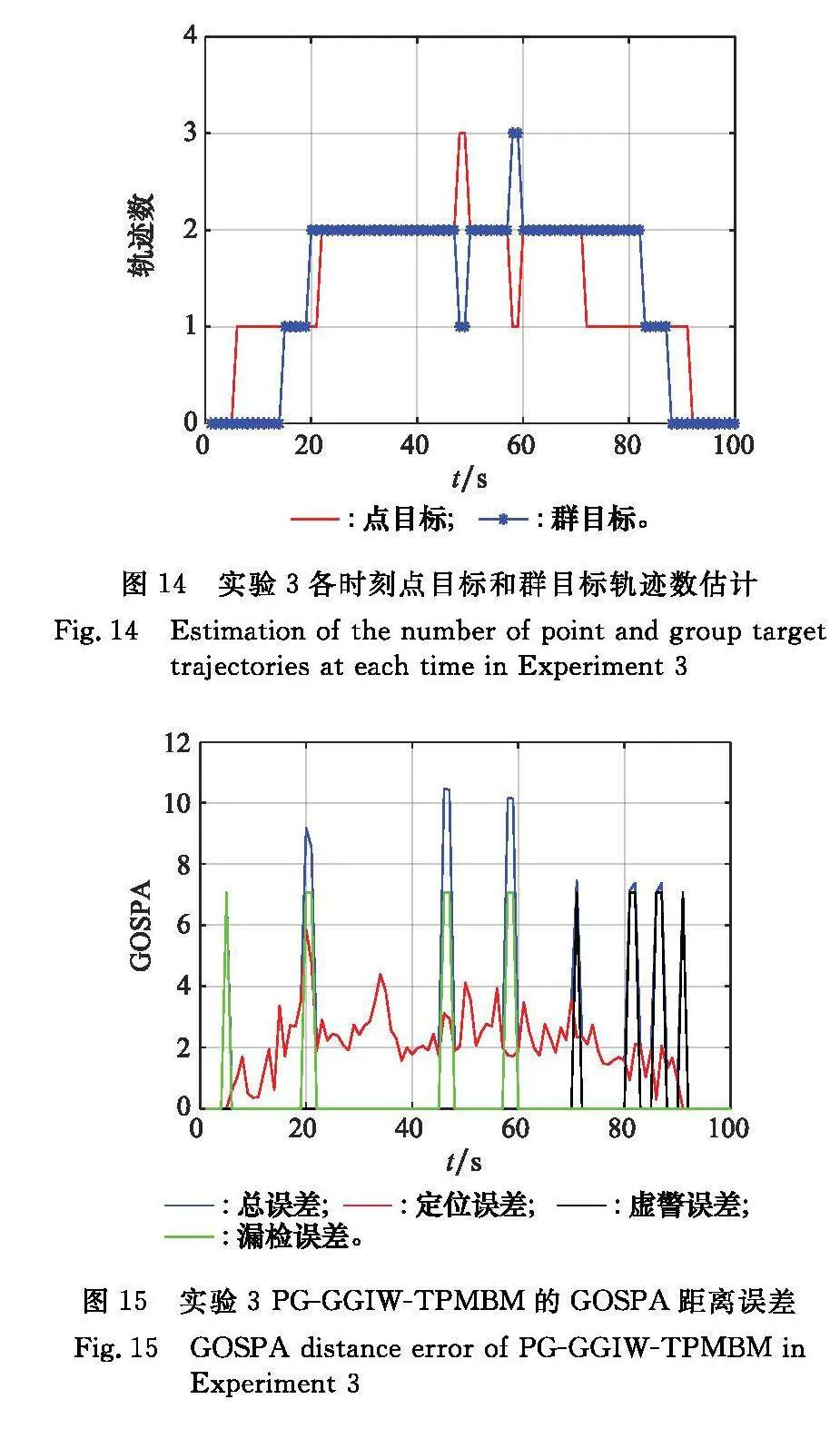
圖11給出了各個目標的運動軌跡和傳感器接收到的量測，每7個時刻標記一次群目標的外形，黑色“*”表示傳感器接收到的目標量測和背景噪聲。圖12和圖13分別給出了PG-GGIW-TPMBM對點群共存目標的跟蹤結果和目標軌跡數量的估計結果，圖14給出了在跟蹤過程中的各項GOSPA距離誤差。

由圖11～圖13可以看出，在跟蹤過程中，PG-GGIW-TPMBM對于目標質心和整體外形依然能夠有效跟蹤。由圖14可以看出，目標1在第46時刻由群目標變成點目標，在該時刻點目標所產生的量測被分配到原群目標的多伯努利分量上。由于群目標存在只匹配到一個量測的情況，由類型概率值判斷此時仍為群目標，當下一時刻依然只匹配到一個量測時，類型概率值增大，目標類別變成點目標。因此，在第48和第49時刻顯示有3個點目標和一個群目標。由于目標4，在第50時刻由點目標變為群目標，在第50時刻產生的量測匹配到原點目標的伯努利分量上，由于量測數大于1，判斷出目標類別為群目標，導致點目標數和群目標數均為2。在第58時刻，由于雜波被分配到點目標伯努利分量上，導致將點目標判別為群目標，由于之后只有點目標的量測一直關聯該目標的伯努利分量，又比較快速地將目標類別轉換為點目標。通過上述實驗，驗證了所提算法在存在目標類別轉換的場景下，對目標狀態、數量和外形依然具有良好跟蹤性能。

4" 結束語

本文主要研究了點群共存場景下基于TPMBM的多目標跟蹤算法。首先將點目標模型和群目標模型相結合，給出了適用于點群共存場景的目標描述方法;然后將其引入GGIW-TPMBM的預測更新過程，提出了可同時對點目標和群目標進行跟蹤的PG-GGIW-TPMBM濾波算法;最后設計仿真實驗證明了所提算法在點目標和群目標共存時，對點目標和群目標進行識別和跟蹤的能力，仍然能夠以較高精度估計目標軌跡及群目標外形，與GGIW-TPMBM算法相比具有明顯優勢。

本文的研究對象主要是點目標和由點目標組成的群目標，隨著傳感器分辨率的日益增加，一個擴展目標在傳感器的每個掃描周期內可能會產生多個量測，從而形成點目標、擴展目標和群目標共存的場景。針對上述場景，下一步工作是對目標的狀態空間和概率密度函數進行改進使所提算法具備更好的泛用性。

參考文獻

［1］ BLACKMAN S S. Multiple hypothesis tracking for multiple target tracking［J］. IEEE Aerospace and Electronic Systems Magazine， 2004， 19（1）： 518.

［2］ VO B N， MALLICK M， BAR-SHALOM Y， et al. Multitarget tracking［M］.London： Wiley， 2015.

［3］ BEARD M， VO T B， VO N B. A solution for large-scale multi-object tracking［J］. IEEE Trans.on Signal Processing， 2020， 68： 27542769.

［4］ ZHANG Y Q， JI H B， HU Q. A fast ellipse extended target PHD filter using box-particle implementation［J］. Mechanical Systems and Signal Processing， 2018， 99： 5772.

［5］ GAN L H， WANG G. Tracking the splitting and combination of group target with δ-generalized labeled multi-bernoulli filter［J］. IEEE Access， 2019， 7： 8115681176.

［6］ LUO Z H. Object tracking for automatic driving［C］∥Proc.of the 2nd International Conference on Computing and Data Science， 2021： 265269.

［7］ YU Q Z， WANG B W， SU Y M. Object detection-tracking algorithm for unmanned surface vehicles based on a radar-photoelectric system［J］. IEEE Access， 2021， 9： 5752957541.

［8］ BONIN-FONT F， ORTIZ A， OLIVER G. Visual navigation for mobile robots： a survey［J］. Journal of Intelligent and Robotic Systems， 2008， 53（3）： 263296.

［9］ KANEZAKI A， NITTA J， SASAKI Y. Goselo： goal-directed obstacle and self-location map for robot navigation using reactive neural networks［J］. IEEE Robotics and automation letters， 2017， 3（2）： 696703.

［10］ ESTER M， KRIEGEL H P， SANDER J， et al. A density-based algorithm for discovering clusters in large spatial databases with noise［C］∥Proc.of the Conference on Knowledge Discovery and Data Mining 1996， 96（34）： 226231.

［11］ FORTUNATO E， KREAMER W， MORI S， et al. Generalized murty’s algorithm with application to multiple hypothesis tracking［C］∥Proc.of the 10th International Conference on Information Fusion. Quebec， QC， Canada： IEEE Press， 2007.

［12］ MAHLER R. Statistical multisource-multitarget information fusion［M］. Boston： Artech House， 2007.

［13］ GARCA-FERNNDEZ F， SVENSSON L， WILLIAMS J L， et al. Trajectory poisson multi-Bernoulli filters［J］. IEEE Trans.on Signal Processing， 2020， 68： 49334945.

［14］ GRANSTRM K， SVENSSON L， XIA Y X， et al. Poisson multi-Bernoulli mixture trackers： continuity through random finite sets of trajectories［C］∥Proc.of the 21st International Conference on Information Fusion， 2018.

［15］ XIA Y X， GRANSTRM K， SVENSSON L， et al. Extended target Poisson multi-Bernoulli mixture trackers based on sets of trajectories［C］∥Proc.of the 22th International Conference on Information Fusion， 2019.

［16］ KOCH J W. Bayesian approach to extended object and cluster tracking using random matrices［J］. IEEE Trans.on Aerospace and Electronic Systems， 2008， 44（3）： 10421059.

［17］ BAUM M， HANEBECK U D. Random hypersurface models for extended object tracking［C］∥Proc.of the IEEE International Symposium on Signal Processing and Information Technology， 2009： 178183.

［18］ KAULBERSCH H， BAUM M， WILLETT P. EM approach for tracking star-convex extended objects［C］∥Proc.of the 20th International Conference on Information Fusion， 2017.

［19］ YANG J L， LI P， GE H W. Extended target shape estimation by fitting B-spline curve［J］. Journal of Applied Mathematics， 2014， 2014： 19.

［20］ 陳振， 李翠蕓， 李想. B樣條曲面三維擴展目標跟蹤算法［J］. 西安電子科技大學學報， 2023， 50（2）： 101111.

CHEN Z， LI C Y， LI X. Algorithm for tracking the 3D extended target based on the B-spline surface［J］. Journal of Xidian University， 2023， 50（2）： 101111.

［21］ 衡博文， 李翠蕓， 李想. 基于MLS的三維擴展目標PMBM跟蹤算法［J］. 系統工程與電子技術， 2023， 45（11）： 34113418.

HENG B W， LI C Y， LI X. 3D extended target tracking algorithm based on moving least square［J］. Systems Engineering and Electronics， 2023， 45（11）： 34113418.

［22］ 宋驪平， 劉宇航， 程軒. 箱粒子PHD演化網絡群目標跟蹤算法［J］. 控制與決策， 2018， 33（1）： 7480.

SONG L P， LIU Y H， CHENG X. Box-particle evolution network PHD filter for group targets tracking［J］. Control and Decision， 2018， 33（1）： 7480.

［23］ 程軒， 宋驪平， 姬紅兵， 等. 標簽箱粒子概率假設密度群目標跟蹤算法［J］. 系統工程與電子技術， 2019， 41（8）： 16771685.

CHENG X， SONG L P， JI H B， et al. Group target tracking algorithm based on labeled box particle probability hypothesis density［J］. Systems Engineering and Electronics， 2019， 41（8）： 16771685.

［24］ VO B T， VO B N. Labeled random finite sets and multi-object conjugate priors［J］. IEEE Trans.on Signal Processing， 2013， 61（13）： 34603475.

［25］ WILLIAMS J L. Marginal multi-Bernoulli filters： RFS derivation of MHT， JIPDA， and association-based MeMBer［J］. IEEE Trans.on Aerospace and Electronic Systems， 2015， 51（3）： 16641687.

［26］ GRANSTRM K， FATEMI M， SVENSSON L. Gamma Gaussian inverse-Wishart Poisson multi-Bernoulli filter for extended target tracking［C］∥Proc.of the 19th International Conference on Information Fusion， 2016： 893900.

［27］ GARCA-FERNNDEZ F， WILLIAMS J L， SVENSSON L， et al. A Poisson multi-Bernoulli mixture filter for coexisting point and extended targets［J］. IEEE Trans.on Signal Processing， 2021， 69： 26002610.

［28］ SU Z Z， JI H B， ZHANG Y Q. Wipa Poisson multi-Bernoulli mixture filter with spawning based on Kullback-Leibler divergence minimization［J］. Chinese Journal of Aeronautics， 2021， 34（11）： 154168.

［29］ DU H C， XIE W X， LIU Z X， et al. Track-oriented marginal Poisson multi-Bernoulli mixture filter for extended target tracking［J］. Chinese Journal of Electronics， 2023， 32（5）： 11061119.

［30］ GARCA-FERNNDEZ F， WILLIAMS J L， GRANS-TRMK， et al. Poisson multi-Bernoulli mixture filter： direct derivation and implementation［J］. IEEE Trans.on Aerospace and Electronic Systems， 2018， 54（4）： 18831901.

［31］ RAHMATHULLAH A S， GARCA-FERNNDEZ F， SVENSSON L. Generalized optimal sub-pattern assignment metric［C］∥Proc.of the 20th International Conference on Information Fusion， 2017.

作者簡介

張雙武（1995—），男，碩士研究生，主要研究方向為多目標跟蹤、隨機集濾波。

李翠蕓（1976—），女，副教授，博士，主要研究方向為多目標跟蹤、隨機集濾波。

趙競哲（1991—），女，工程師，碩士，主要研究方向為目標跟蹤與智能規劃。

衡博文（1998—），男，碩士，主要研究方向為多目標跟蹤、隨機集濾波。