導學“勾股定理”，感悟數形結合

第3章 勾股定理

領" 銜" 人：李庚南（正高級教師、江蘇省特級教師）

組稿團隊：江蘇省李庚南數學教學研究所

勾股定理被譽為“千古第一定理”，它刻畫了直角三角形三邊的關系，由“形”定“數”，體現了“數”與“形”的完美結合。

勾股定理的學習包含對勾股定理的探索、發現以及證明的過程，是對三角形性質的深入學習，有助于同學們了解直角三角形三邊之間的關系，掌握直角三角形的性質，理解從特殊到一般的數學思想。勾股定理逆定理的證明則體現了數學思維的嚴謹性，為后續數學學習奠定基礎。

直角三角形是一種常見而特殊的三角形，它有許多性質，如兩個銳角互余、30°的角所對的直角邊等于斜邊的一半等。勾股定理指出了直角三角形三邊的數量關系，這為我們在幾何圖形和數量關系之間搭建了一座橋梁，從而發揮了它重要的作用。

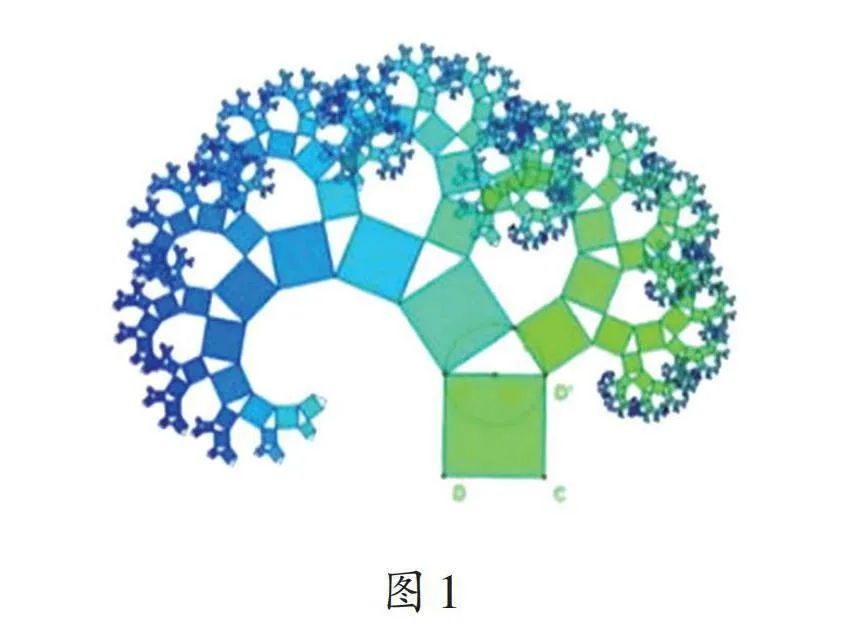
相傳，畢達哥拉斯從觀察地面圖案的面積關系發現了直角三角形三邊的平方關系。畢達哥拉斯還畫出一個可以無限重復的圖形，又因為重復數次后的形狀好似一棵樹，所以該圖形被稱為畢達哥拉斯樹（如圖1）。

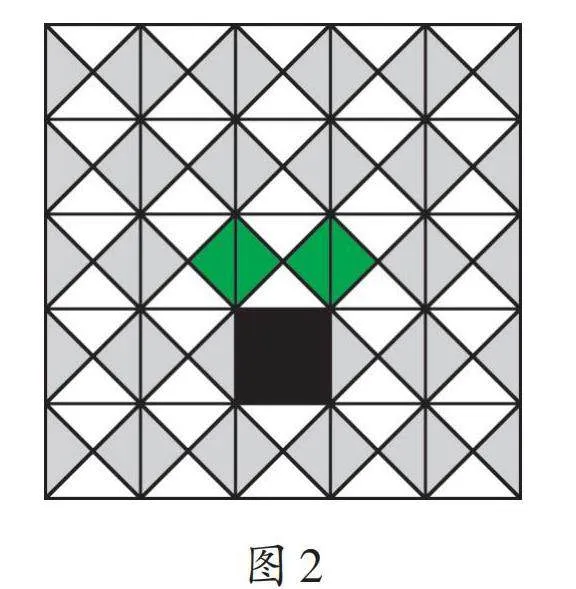
我們也可以通過觀察繼續研究。例如，研究等腰直角三角形這種特殊直角三角形的面積關系。通過觀察，我們可以從圖2中發現，以兩直角邊為邊長的小正方形的面積之和等于以斜邊為邊長的正方形的面積，從而得出三邊之間的數量關系。

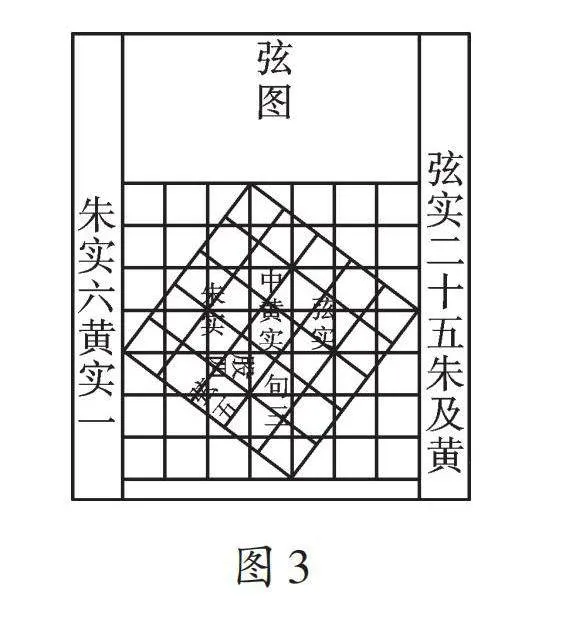
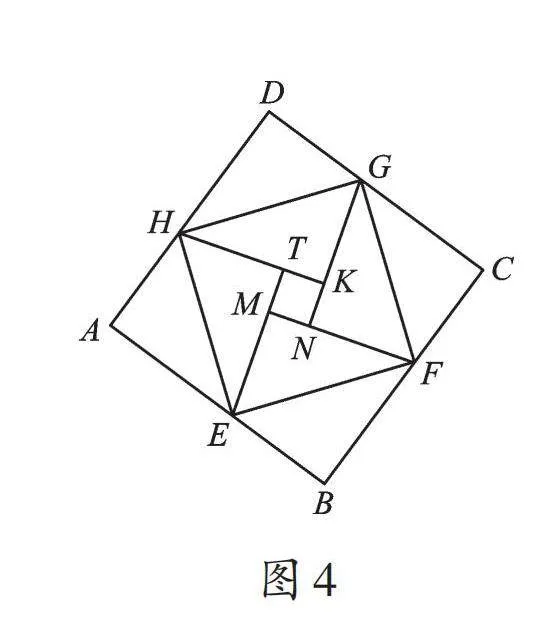
圖3是我國漢代數學家趙爽創制的一幅弦圖，后人稱其為趙爽弦圖。這也是一種面積證法。如圖4，它的依據是圖形在經過適當切割后再拼接成一個新圖形，切割前和拼接后圖形的各部分的面積之和不變。趙爽所用的這種方法是我國古代數學家常用的“出入相補法”。當然，勾股定理證明方法很多，感興趣的同學可以查閱資料，了解更多的證法。

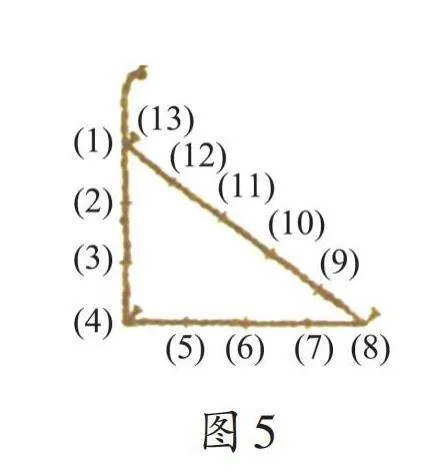
據說古埃及人是用圖5的方法畫直角的：把一根長繩打上等距離的13個結，然后分別以三個、四個、五個結間距的長度為邊長，用木樁釘成一個三角形，其中一個角便是直角。相傳，我國古代大禹治水時也是用類似的方法確立直角。

我們可以據此提出猜想：如果三角形的三邊滿足兩邊的平方和等于第三邊的平方，那么這個三角形是直角三角形。有興趣的同學可以查閱教材或相關資料，了解關于“勾股定理逆定理”的證明方法。

（作者單位：江蘇省海安市城南實驗中學）