融合信息技術的高中物理創新微課程設計

摘 要：以“運動的合成與分解”章節中的“繩”模型速度關聯問題為例，基于SOLO分類理論設計了多維素養遞進式微課程，并進行了實踐。探討在TPACK視角下融合信息技術的高中物理創新教學及評價方式，以期更有效地落實物理學科核心素養的培養。

關鍵詞：高中物理；創新微課程；信息技術；速度關聯；TPACK

中圖分類號：G633.7 文獻標識碼：A 文章編號：1003-6148（2024）10-0084-3

收稿日期：2024-04-15

基金項目：廣東省中小學教師信息技術應用能力提升工程2.0專項科研課題“在中學物理創新課程中融合信息技術的實踐研究”（TSGCKT2023102）。

作者簡介：陳宏林（1986-），男，中學高級教師，主要從事中學物理信息化教學研究。

《普通高中物理課程標準（2017年版）》明確指出，高中物理教材應有效地利用信息技術［1］。這包括通過信息技術平臺獲取課程資源、利用信息技術進行互動交流以及使用信息技術工具進行輔助教學等方面。目前，在國內的中學物理教學中，信息技術的應用主要是以輔助教學為主。例如，在課堂教學中使用PPT或動畫演示，或者在物理實驗中使用數字采集器等。缺少對信息技術的深度融合，不利于提升學生的信息素養和物理核心素養。本文以“運動的合成與分解”中有約束的“繩”速度關聯問題為例，基于TPACK和SOLO理論設計了一套深度融合信息技術的物理創新微課程。

1 TPACK及SOLO理論簡介

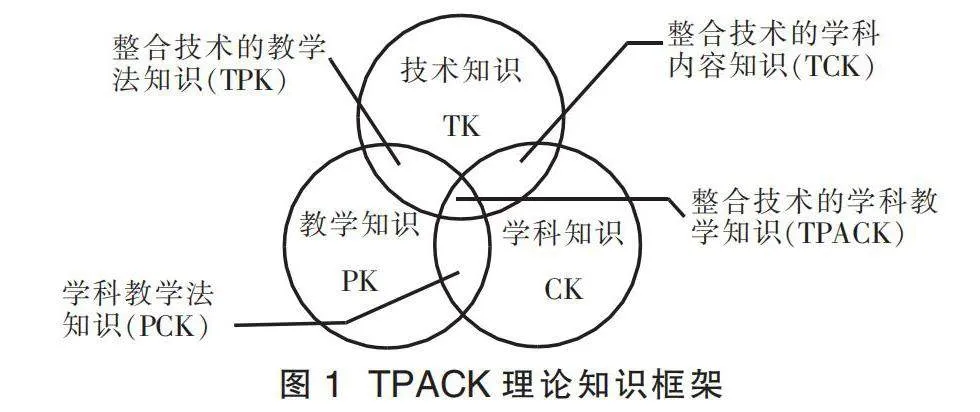
TPACK（Technological Pedagogical Content Knowledge）即整合技術的學科教學知識，由學者科勒和米什拉于2005年在舒爾曼的學科教學知識PCK的基礎上提出的［2］。它包含了學科知識、教學知識、技術知識以及它們相互交融衍生出來的整合性知識（圖1），它既強調信息技術的有機組成，又深刻指向學科素養，是物理學科信息技術融合教學的重要理論工具。

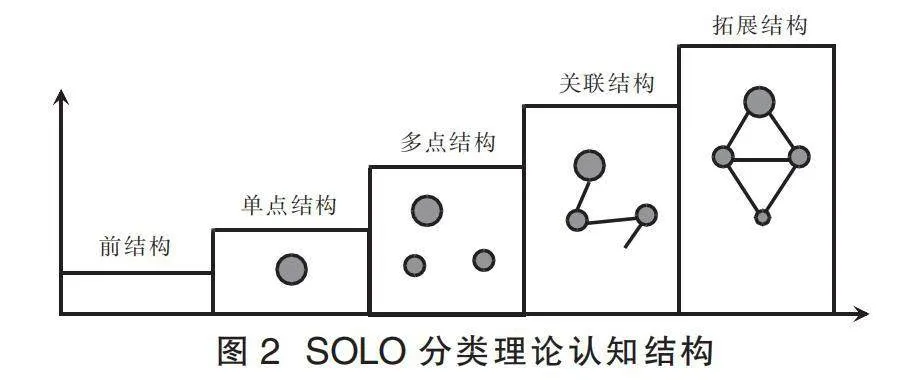
SOLO分類理論是由皮亞杰的認知階段理論發展而來，它提供了可觀察的學習成果的結構。該理論將學習成果（思維層次）劃分為五個邊界清晰且易于測量的結構（圖2），包括前結構、單點結構、多點結構、關聯結構和拓展結構。這五個結構與高中物理學科核心素養的五個水平相對應，可在TPACK框架下作為融合教學評價的理論工具。

2 速度關聯問題微課程前設計

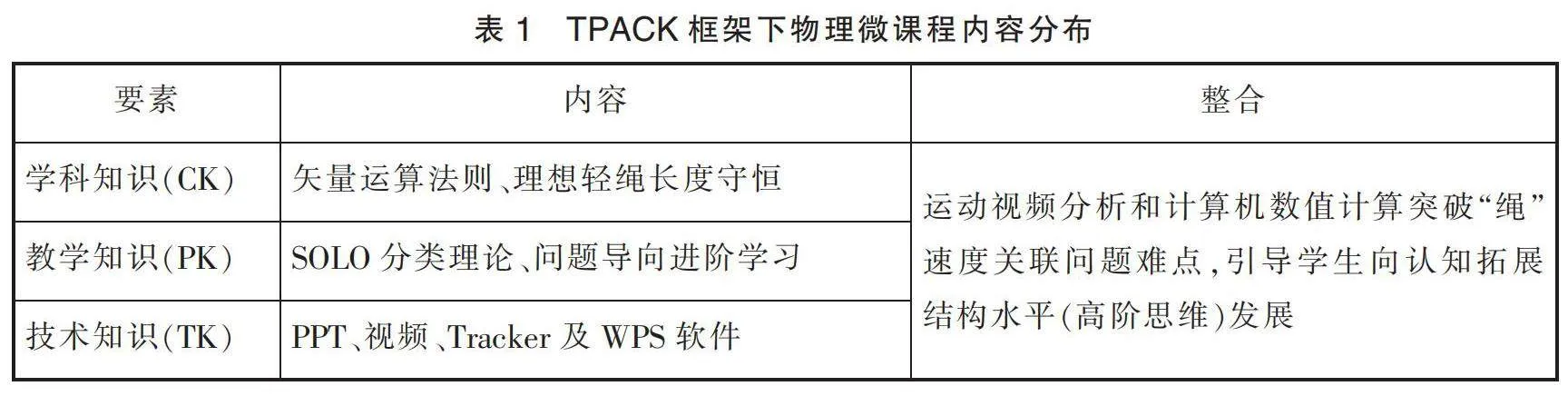
在高中物理必修二“運動的合成與分解”中，速度關聯是一個難點。特別是在有約束的情況下，學生更難準確解決該難點。其根源在于學生對于運動正交分解的獨立性缺乏深刻的理解。基于此，以一道有約束的“繩”模型速度關聯問題為例，運用TPACK框架，整合情境問題、SOLO分類理論、視頻分析以及計算機數值模擬等多個元素，設計了一套創新的微課程（表1），力求覆蓋學生認知發展的所有水平，以促進學生高階思維的發展。

3 微課程教學環節實施與評價

3.1 “繩”模型速度關聯問題簡單情境——前結構、單點結構

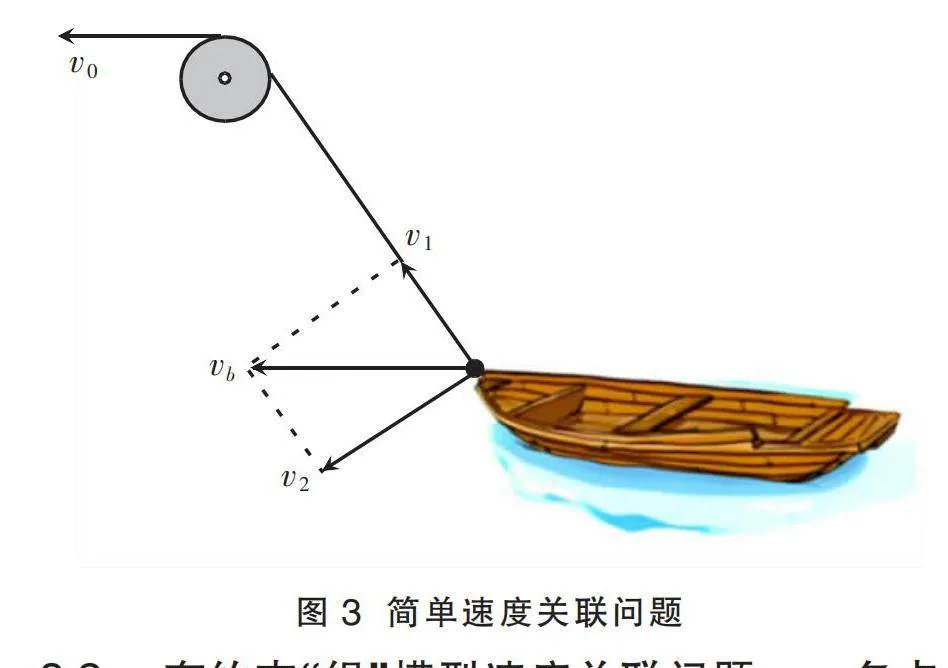
如圖3所示，通過視頻和PPT展示簡單的“繩”模型速度關聯問題。師生共同探討速度分解的平行四邊形法則，研究了小船與繩連接點的速度及方向，并最終確定將連接點的運動分解為沿著“繩”方向的收縮分運動，以及以滑輪為中心且垂直于“繩”的擺動分運動。需要注意的是，擺動分運動對于滑輪和小船之間的繩長變化沒有影響。在這個過程中，學生逐漸形成了矢量運算法則、分運動的獨立性以及輕繩長度守恒等方面的單點認知。

3.2 有約束“繩”模型速度關聯問題——多點結構

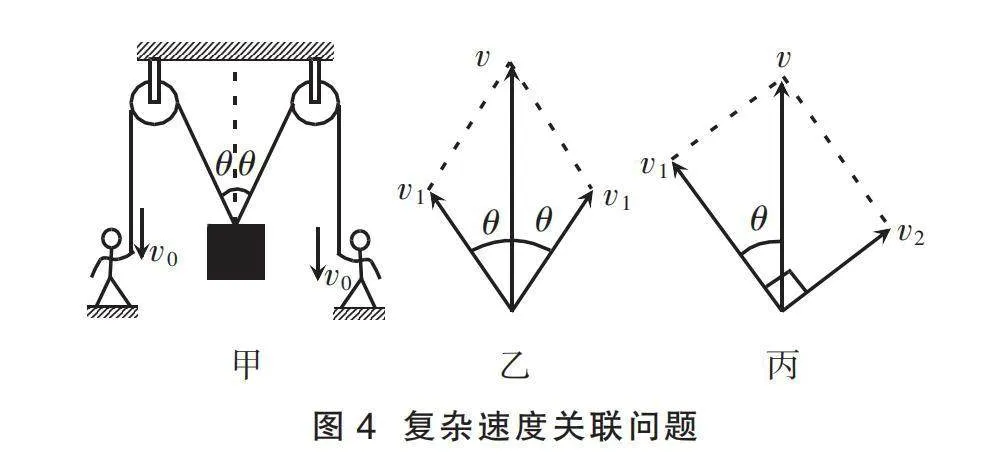
如圖4甲所示，兩根不可伸長的繩索繞過定滑輪系在木箱上端，兩人以豎直向下的恒定速度v0拉繩索，當繩索與豎直方向的夾角均為θ時，求木箱速度大小。

方法一：如圖4乙所示，令物體上升速度為v，沿兩繩分解，分速度為v1，則有：v=2v1cosθ。由速度關聯v1=v0，得v=2v0cosθ。

方法二：如圖4丙所示，考慮對稱情況，等效為物體沿一根豎直桿上升，速度沿繩和垂直于繩分解，v1=vcosθ。由速度關聯v1=v0，得v=v0 /cosθ。

以上兩種木箱速度的分解方法均依據矢量運算法則，且沿繩分速度關聯相等，為何會得到兩種不同的結果？通過此環節引入思維沖突，激發學生形成對矢量投影和正交獨立性各知識點的關聯認知。

3.3 利用視頻分析和數值模擬進行實證研究——關聯結構

師生共同探討了對以上結果進行驗證的技術手段，包括頻閃照相、速度傳感器、視頻分析軟件Tracker以及常用辦公軟件WPS等。

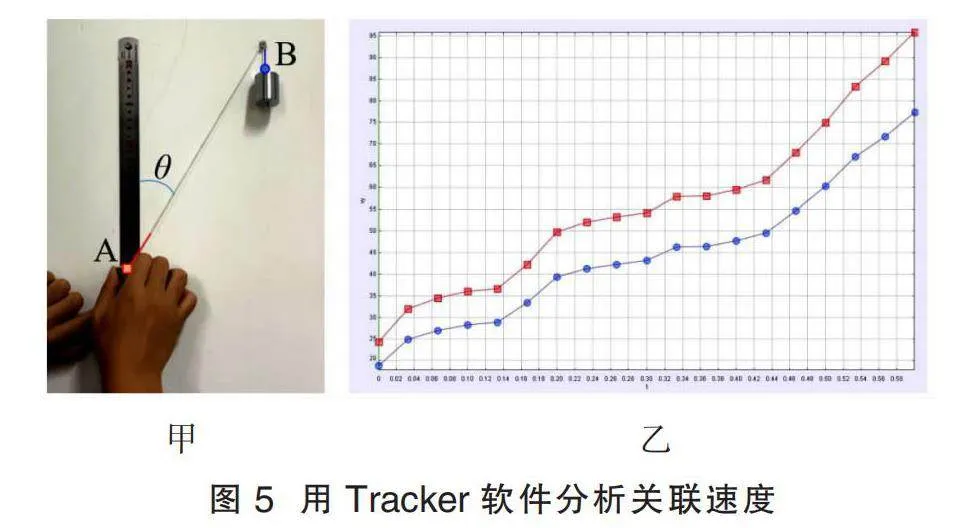
第一小組學習了如何使用Tracker軟件，包括創建質點、自動搜索和分析等步驟。他們錄制了視頻并將其導入軟件進行分析，將質點A的速度進行正交分解，并與質點B的速度進行比較，如圖5甲所示。通過分析圖5乙的結果，可以得知這兩個速度都是變化的，并且變化趨勢是一致的。然而，由于軟件在角度跟蹤分析方面存在誤差，手機錄像的幀率較低，以及手動拉動物體運動變化不均勻等原因，導致兩個速度之間存在差異，無法得出確切的結論。

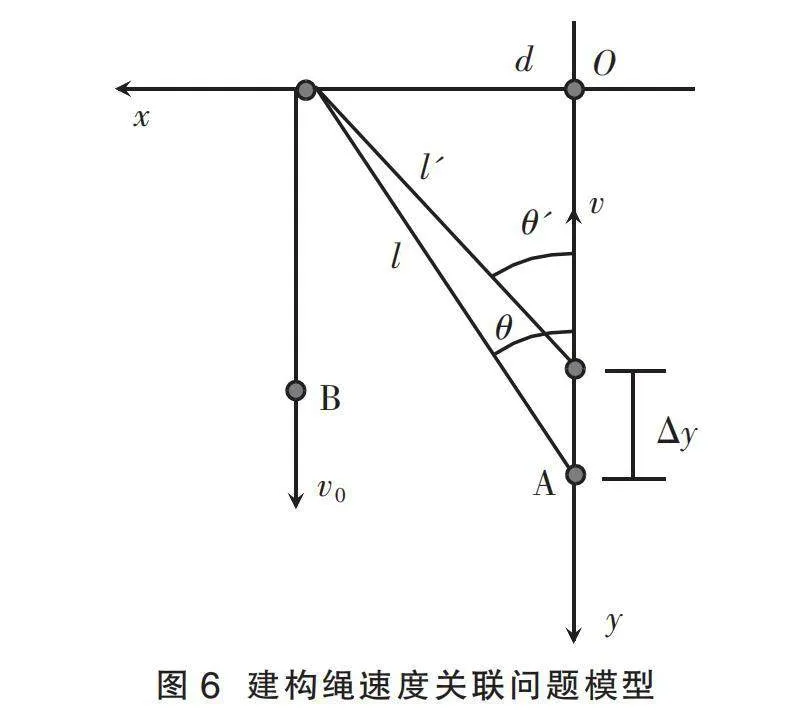
另一小組則建構了一個理想運動模型，如圖6所示。圖中，質點A和B分別代表與“繩”關聯的兩個端點。他們利用WPS進行數值模擬計算，這種方法操作簡便易上手，只需在表格中編寫公式進行遞進運算。雖然這種方法相對比較原始，但它是大型數值計算的基礎，有助于提升學生的信息素養水平。

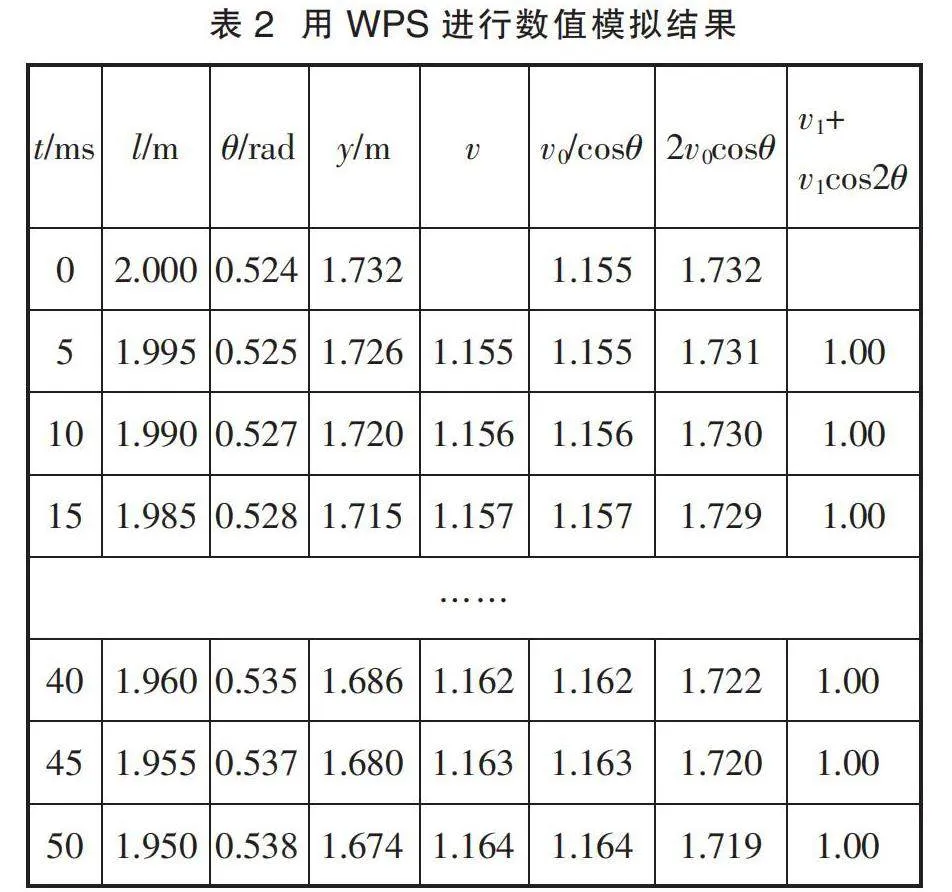
先對系統進行初始化，令d=1 m、v0=1 m/s、θ0=30°，質點B以v0向下勻速運動，計算步進為Δt=0.005 s。質點A的近似速度為v=Δy/Δt，v0 /cosθ和2v0cosθ兩值取Δt內初、末時刻速度的均值。對比這三個速度計算值，結果如表2所示。

對表2分析可知，方法二的結果是正確的。若將質點A的速度沿兩繩分解，由于兩分量并非正交，另一分量對沿繩分量的“收縮”運動有影響。若將此分量進一步投影到繩方向，可得到v1+v1cos2θ=v0。因此，解決此問題的關鍵在于“繩不可伸長”這個約束條件。從能量角度看，輕繩對兩端點連接的物體做功之和為0，即Tvcosθ-T'v0=0。至此，學生可形成對矢量運算相關知識點的關聯認知。

3.4 非正交矢量運算問題——拓展結構

通過以上內容的學習，學生能理解垂直于繩子的擺動分速度不影響沿繩的收繩分運動，即正交情況下兩個分運動完全獨立。這種矢量的正交獨立性在其他矢量運算問題中是否也存在呢？

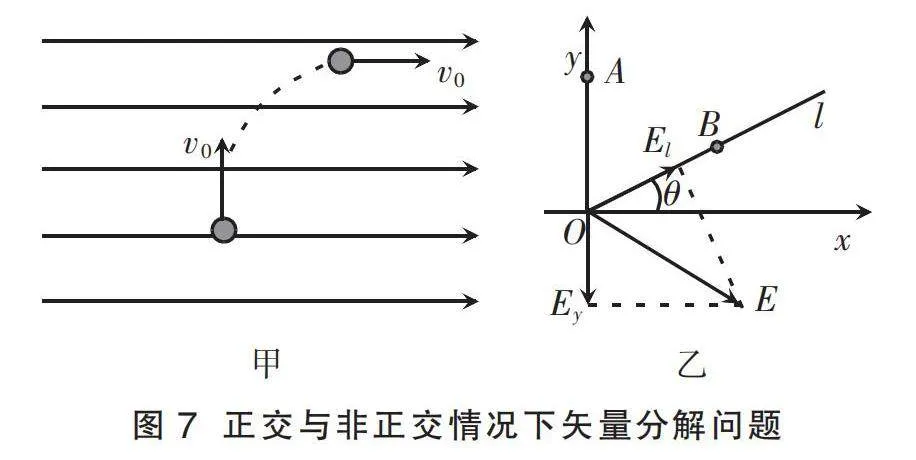
在如圖7甲所示的正交力場中，動能定理可以單獨“應用”在豎直方向或水平方向。在如圖7乙所示的勻強電場中，建立直角坐標系xOy，已知OA=OB=1 cm，φO=1 V，φA=2 V，φB=0 V，θ=30°。由場強與電勢差的關系E=U/d，求得y和OB方向的分場強，再合成出合場強的結果是錯誤的。

在非正交情況下，電勢差的變化不僅與該方向的分場強相關，還受到另一方向分場強的影響，即電勢在某個方向上的變化是由合電場決定的。通過解決這個問題，關于“矢量正交獨立性”的認知由“速度關聯問題”拓展到各類矢量運算，使ND1vRA83gbF0imW31ak2Sg==學生的認知達到了更高的層次。

4 結 語

從有約束的“繩”模型速度關聯問題出發，拓展到其他矢量投影問題，突破了思維慣性，使學生從低階思維向高階認知轉變，并利用SOLO分類評價將多個維度的素養整合在一起。開創了高中物理創新微課程的新思路和新方式，有助于物理學科核心素養的培養。

參考文獻：

［1］中華人民共和國教育部.普通高中物理課程標準（2017年版2020年修訂）［S］.北京：人民教育出版社，2020.

［2］黃全安，郭洋.TPACK視角下高中物理教學的路徑優化——以“自由落體運動”教學為例［J］.物理教學，2024，46（2）：16-20.

［3］Deng X M，Wang M H，Chen H L，et al. Learning by progressive inquiry in a physics lesson with the support of cloud-based technology［J］. RESEARCH IN SCIENCE & TECHNOLOGICAL EDUCATION，2019（6）：308-328.

（欄目編輯 賈偉堯）