基于CUDA的Scharr算子并行化研究

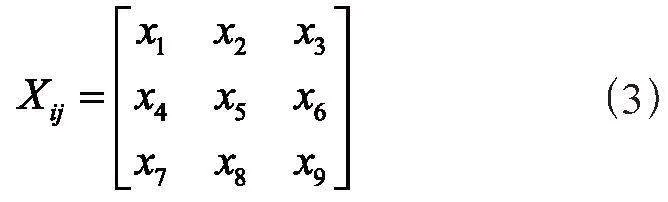
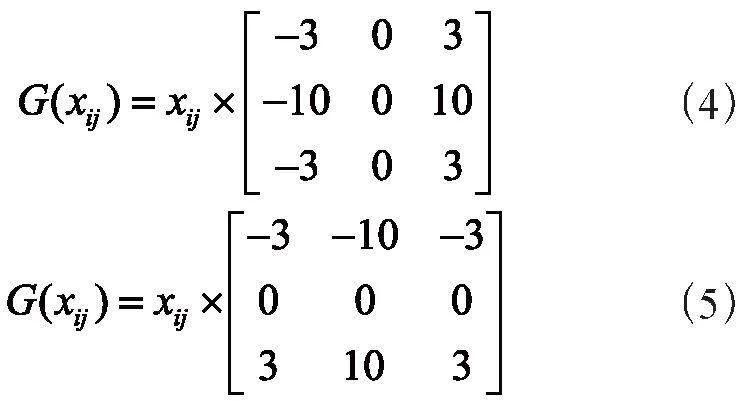
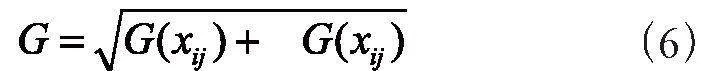
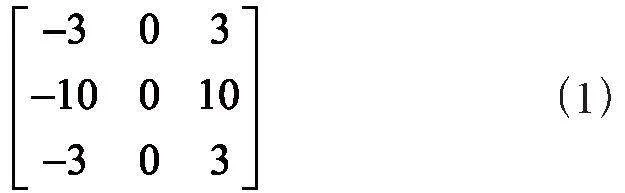
摘 要：傳統邊緣檢測算子采用逐行求梯度的方法順序進行，遇到圖像尺寸大或計算速度高效時，較難勝任這類計算密集度高的需求。文章從并行化角度對Scharr算子進行設計，采用CUDA語言對二維數據并行計算上進行算法優化，提出了多線程塊偏移計算的設計思路，同時采取流處理的方式縮短傳輸開銷。實驗結果表明，與傳統Scharr算子相比，在7 000×7 000尺寸圖像識別上呈現了高效的識別速度，加速比提高了300倍左右，有較高的應用價值。

關鍵詞：邊緣檢測；Scharr算子；并行計算

中圖分類號：TP391.4 文獻標識碼：A 文章編號：2096-4706（2024）16-0044-05

Research on Parallelization of Scharr Operators Based on CUDA

Abstract： Traditional edge detection operators use the method of seeking gradients row by row in order， which makes it difficult to meet the high computational density requirements of large image sizes or high computational speed. This paper designs the Scharr operator from the perspective of parallelization， optimizes the algorithm on two-dimensional data parallel computing using CUDA language， proposes a design idea for multithreaded block offset calculation， and adopts stream processing to reduce transmission overhead. Experiment results show that compared with the traditional Scharr operator， it exhibits efficient recognition speed in image recognition of sizes on 7 000×7 000， with an acceleration ratio increased by about 300 times， and has high application value.

Keywords： edge detection; Scharr operator; parallel computing

0 引 言

目前，人工智能的普及應用和發展成為技術領域的研究熱點，基于Opencv庫的使用和機器視覺技術的運用使得圖像識別領域有廣闊的研究空間。其中針對卷積層的卷積核來說，邊緣檢測算子就是其中對圖像起到濾波信息提取作用，而圖像特征提取是否充分影響后續識別精度，因此對邊緣檢測卷積算子的研究有利于提高對圖像邊緣信息特征的識別。

傳統針對圖像邊緣檢測算子有Canny[1-3]、Sobel[4-6]等一階邊緣算子，二階邊緣算子如拉普拉斯算子[7]、高斯拉普拉斯算子和高斯差分算子等。李浩誼等人基于改進的Scharr算法的海上艦船圖像邊緣檢測[8]，在傳統Scharr的基礎上對算子在方向進行改進，增加了0°、45°、90°和135°四個方向，提高了算子檢測的完整程度。李浩誼等學者采用多方向Scharr的齒輪邊緣檢測與中心定位方法[9]，增加到8個方向，用5×5算子模板進行檢測，最終減小了噪聲的影響。蔣潔琦等學者對表面弱邊緣瑕疵檢測算法及應用[10]，結合力形態學開閉濾波，達到增強弱邊緣的效果。林麗等學者提出了一種具有抗噪聲能力的圖像清晰度評價函數[11]，增加到4個方向進行梯度檢測，減小算法計算量同時提高了精度，獲得理想的效果。

隨著顯卡的普遍應用，計算能力得到飛速提高大部分得益于顯卡加速，在復雜計算中，針對算法中可并行的重復計算子過程考慮采用CUDA語言或Opencl等語言對CPU代碼進行重新程序設計。以實現在高密集度計算上得到提升。如趙志建等學者提出了基于CUDA并行優化的矩陣相乘算法研究[12]，有效提升了吞吐量，利用了共享內存的資源。采用共享內存可以降低延遲。本文采用CUDA框架優化Scharr算子從而提升性能。

1 Scharr算子介紹

該算子是在Sobel算子的基礎上做了改進，實現了差異性的增強，因此二者的濾波原理是一樣的。采用3×3卷積核對圖像每個像素點進行運算，通過算子上權值來實現凸顯像素之間的差異化。下面介紹x方向上的一階Scharr模板。

y方向上一階算子模板如下：

圖像任意區域矩陣表示如下：

求梯度過程如下：

計算總梯度：

求閾值，總體上求出全像素圖像上平均閾值作為判定像素是否為邊界點：

其中?x、?y分別為水平和垂直兩個方向灰度值的落差，e為圖像全局范圍內的最大落差。

2 Scharr算子計算流程

Scharr算子計算過程如：

1）對算子賦初值。

2）對原始的灰度圖像外圍添加一圈0，作為padding的填充，主要是考慮到作為3×3的卷紙算子來說，大部分處理集中在算子中心區域，對于圖像邊緣一圈的計算相對少，故而添加一圈padding填充，增大了卷積核的感受視野。

3）求取閾值T，從兩個方向進行，如從x方向和y方向進行求取，求取過程以x方向為例：沿著水平方向逐行對相鄰兩個像素灰度值進比較，經過一輪比較即可比較出max差值和min差值，同時需要注意到雖然圖像是二維呈現的，在循環便利中需要進行跨越一行偏移。

4）進行算子求梯度運算，由于數據是二維呈現的，在進行跨行偏移時，在局部范圍內增設小循環窗口，如i，j窗口步長為3，即可獲取到（x，y）當前位置的鄰域范圍內的3×3區域。

CPU偽代碼如下：

3 使用CUDA設計

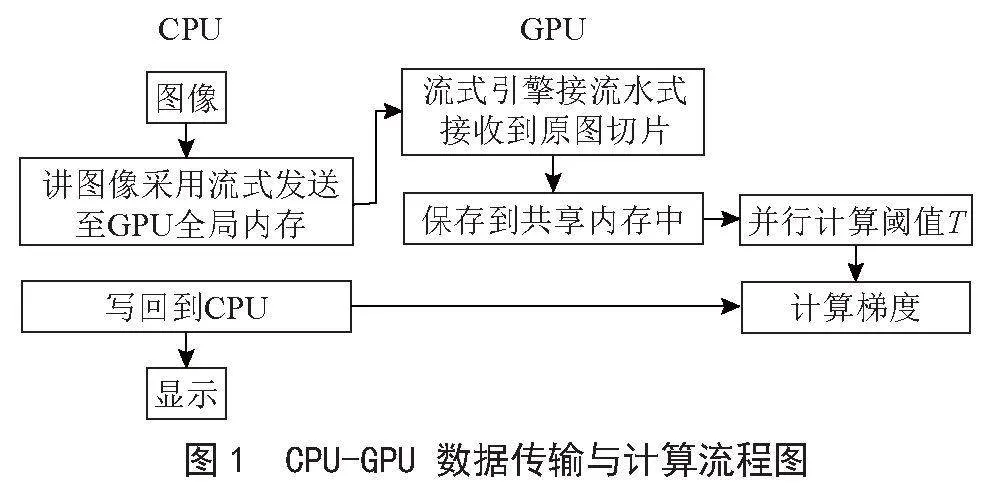
對CPU程序的并行設計流程如圖1所示。

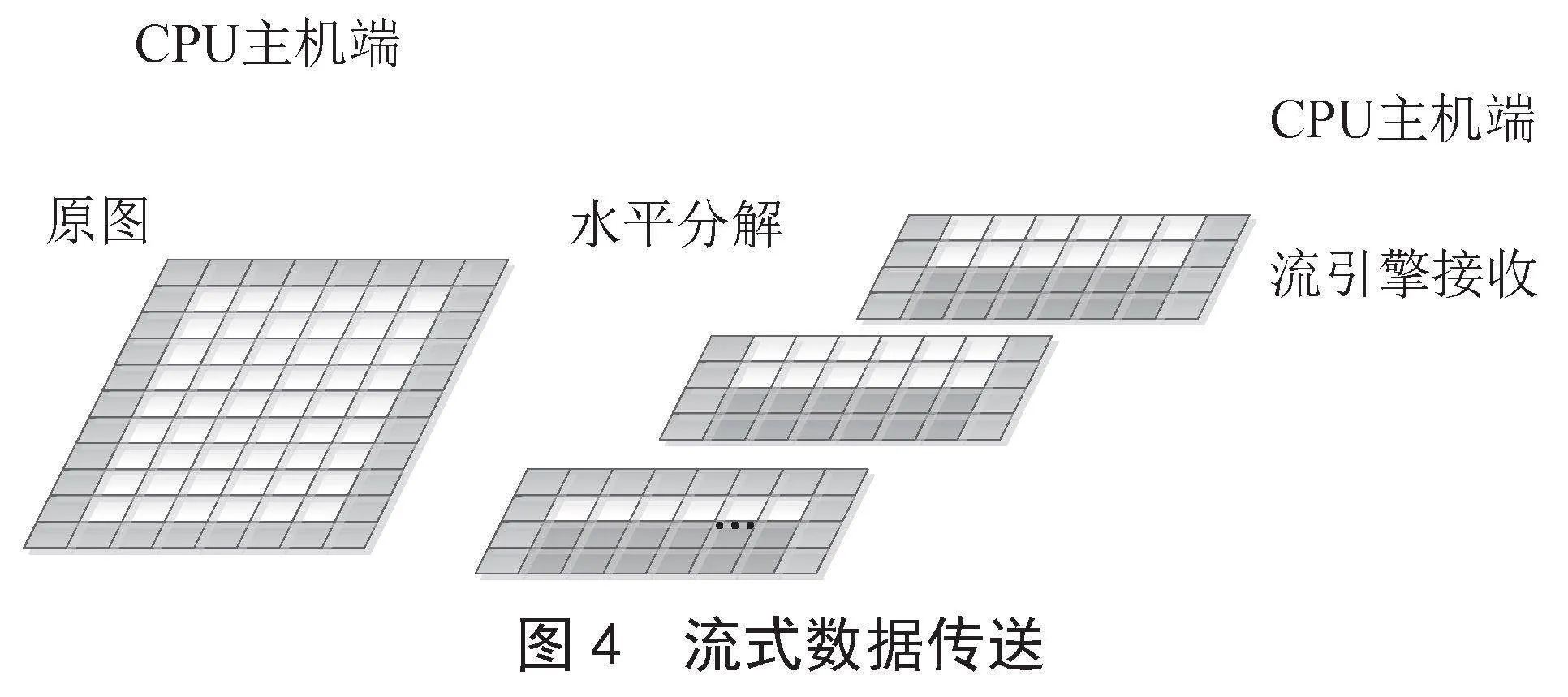
從流程，體現了CUDA并行程序設計的總體思路，考慮到充分利用數據的總線傳送時間，采用常用的CUDA流技術，充分利用了傳送數據時間，在傳輸數據的同時，開始了共享內存中計算任務。

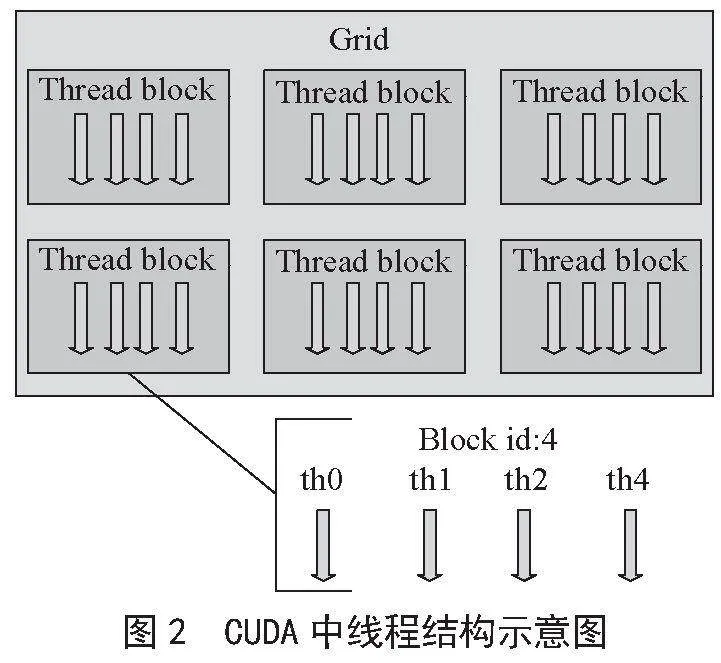
主要尋求計算過程中，批量簡單的操作進行改進，同時還要結合CPU-GPU數據傳輸開銷綜合設計，避免過多邏輯判斷的原則。這都基于GPU硬件體系結構而決定，如圖2所示

在CUDA體系結構中，一個Grid計算單元含有多個計算塊block，每個計算塊block。如示例中有6個block塊，每個塊含有4個thread線程。

訪問如下：

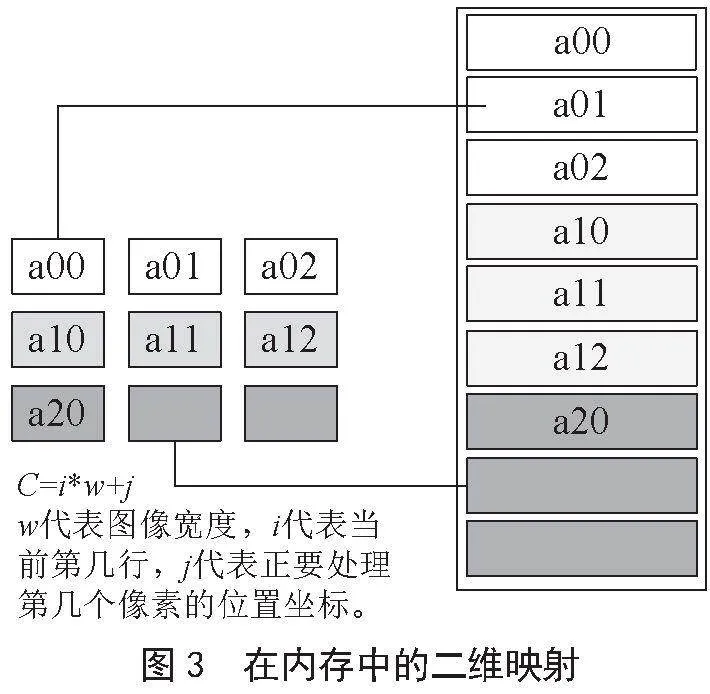
下面從內存布局角度分析如圖3所示。

由于共享內存的容量空間是有限的，需要對共享內存的數據做初始化，初始化之后可以讓更多的線程同步__syncthreads（）。

4 算法并行化設計

近年來顯卡普遍運用到人工智能的各個領域中，與GPU有著并行計算單元，更適合處理計算邏輯少，大量并行計算任務，而CPU更適合于多任務進程計算，邏輯控制單元豐富，對于復雜的邏輯控制，更擅長。CUDA編程中CPU-GPU之間送數據也會占用大量的時間，如何處理好傳送數據時間與核函數的計算時間是提升加速性能的關鍵，計算單元內部利用共享內存提高單元性能。

本文對CPU代碼中兩個部分進行流程改寫，進行并行程序設計，偽代碼如下：

5 并行開銷

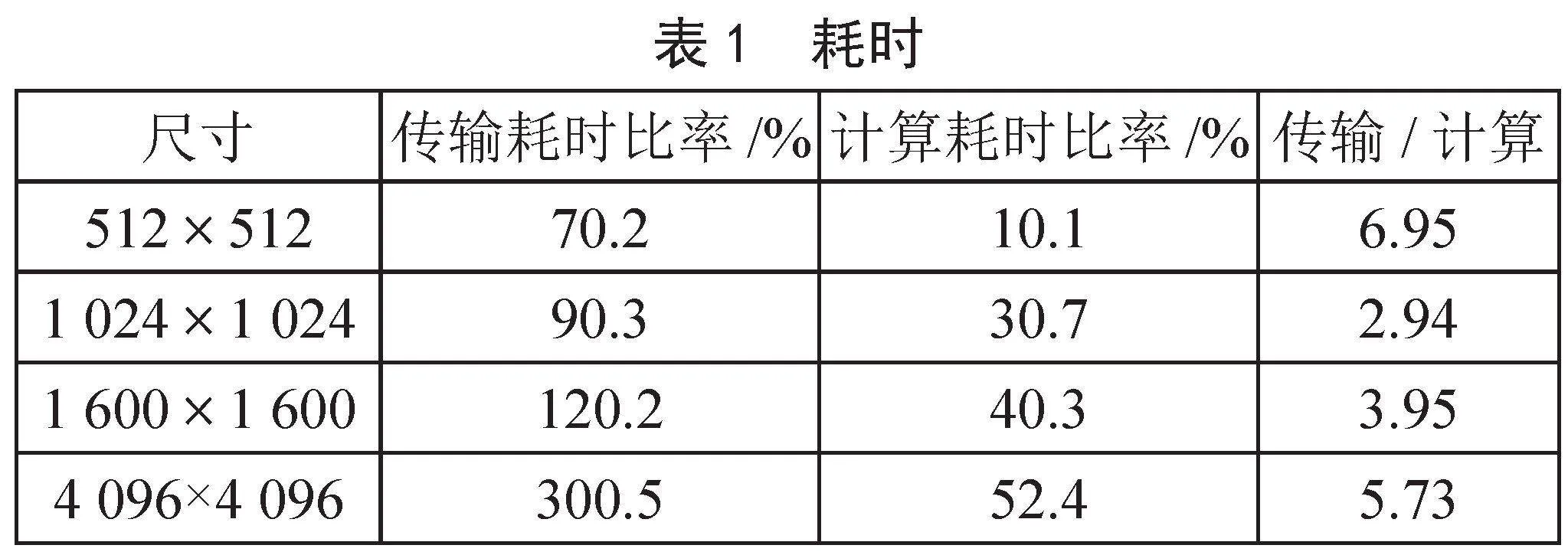
當圖像較小時，雖然采用流式切片方式傳送數據，但數據尺寸小，浪費在主板上時間會比單純CPU代碼耗時久。例如圖像尺寸在500×500時，傳輸耗時較大，隨著圖像尺寸逐漸增大，計算與傳輸耗時相比，優勢明顯，獲得速度提升。如表1所示。

從表1可以看出，小尺寸上計算耗時很小，大部分時間浪費在主板數據傳輸上，在大尺寸上，傳輸耗時也很大，主要在對原圖進行水平切片，按切片進行傳送子圖，但計算耗時不大。示意圖如圖4所示。

6 實驗分析

CP78ffb23fa79fe510a5e7dc295d40e7aef00989c877145c18fdc4c0f2eac7382fU配置如下：Intel Xeon CPU E5-2620，32 GB RAM。

GPU配置如下：全局內存8 GB，每block最多含1 024個線程，CUDA處理核3 840個。

為了測試不同尺寸的數據，采用OpenCV對原圖進行尺寸放大，最大到7 000×7 000，測試加速比如表2所示。

從表2可見在小尺寸上加速不明顯，由于傳送耗時和資源加載開銷，導致總體加速比并不理想，在大尺寸上表現較好，充分利用了流與計算單元荷載。

7 實驗效果

如圖5所示，Scharr過濾結果能夠清晰分辨出紋理走向，相比Sobel體現出來了檢測點附近的權重值較大，從而中心點鄰域點對最終處理起到了增強的效果。Scharr過濾算子對于邊緣模糊的情況很適合使用。

8 結 論

本文采用CUDA對傳統的CPU程序進行設計優化，提出了基于CUDA的Scharr檢測研究。研究從分析Scharr程序開始著手，通過切片法，將整個圖切成不同的子圖流式發給GPU，對于小尺寸來講加速比并不理想，主要是時間耗費在資源初始化開銷方面上。對于大尺寸圖像來說，由于采取了分片流式并行計算，充分利用了流在同一時間傳輸和計算同時進行的優勢，充分利用了GPU線程資源，同時也還原了Scharr算法。今后考慮在融合多方向模板去進一步優化Scharr算子本身，在算法精度提高方面進一步研究。

參考文獻：

[1] 李平陽，孫志毅.一種提升Canny算子的自適應邊緣檢測方法 [J].太原科技大學學報，2013（3）：171-174.

[2] 馬新星，徐健，張健.一種基于自適應Canny算子的艦船紅外圖像邊緣檢測方法 [J].紅外，2013（7）：25-30.

[3] 汪宗洋，王煜，朱碩.基于改進Canny算法的邊緣檢測技術應用及發展趨勢 [J].信息通信技術與政策，2023（8）：90-96.

[4] RAKESH R，VINAY A. Edge Detection Using Guided Sobel Image Filtering [J].Wireless Personal Communications，2023，132（1）：651-677.

[5] 樸思儒，李彬，張赫，等.基于多方向擴展Sobel加權算法的合作目標檢焦方法研究 [J].機電工程術，2023（5）：131-134.

[6] 薛文格，鄺天福.基于Sobel算子和灰色關聯分析的圖像邊緣檢測 [J].楚雄師范學院學報，2023（3）：135-140.

[7] LUIS J P D，REYES E G. Analysis of a fire Extinguishing Model with a p-Laplacian Operator and with Non-Linear Advection and Reaction [J/OL].Physica Scripta，2023，98（8）[2024-01-09].https：//iopscience.iop.org/article/10.1088/1402-4896/ace08c.

[8] 李浩誼，馬春庭.基于改進的Scharr算法的海上艦船圖像邊緣檢測 [J].艦船電子工程，2019（3）：103-106.

[9] 李浩誼，馬春庭，唐秀媛.多方向Scharr的齒輪邊緣檢測與中心定位 [J].工具技術，2019（2）：130-133.

[10] 蔣潔琦，楊庚，劉沛東，等.表面弱邊緣瑕疵檢測算法及應用 [J].計算機技術與發展，2019（5）：142-147.

[11] 林麗，李詩云，陳健.一種具有抗噪聲能力的圖像清晰度評價函數 [J].重慶郵電大學學報：自然科學版，2022（2）：223-233.

[12] 趙志建.基于CUDA并行優化的矩陣相乘算法研究 [J].智能計算機與應用，2022（11）：192-196.