核心素養(yǎng)視域下學(xué)生推理意識培養(yǎng)策略

摘要：推理意識是學(xué)生必備的數(shù)學(xué)核心素養(yǎng)之一，推理意識有助于學(xué)生養(yǎng)成講道理、有條理的思維習(xí)慣，是形成推理能力的經(jīng)驗(yàn)基礎(chǔ).在小學(xué)數(shù)學(xué)教學(xué)中，教師要引導(dǎo)學(xué)生經(jīng)歷初步的邏輯推理過程，通過創(chuàng)設(shè)真實(shí)的情境、加強(qiáng)動手操作、制造思維沖突以及重視說理思辨等策略，幫助學(xué)生形成初步的推理意識，讓學(xué)生學(xué)會用數(shù)學(xué)的思維思考現(xiàn)實(shí)世界，使數(shù)學(xué)更具嚴(yán)謹(jǐn)性.

關(guān)鍵詞：核心素養(yǎng)；推理意識；培植策略

《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）》指出：“數(shù)學(xué)思維主要表現(xiàn)為：運(yùn)算能力、推理意識或推理能力.”［1］通過推理意識的培養(yǎng)，學(xué)生能逐步養(yǎng)成講道理、有條理的思維習(xí)慣，同時形成實(shí)事求是的科學(xué)態(tài)度.

1類比遷移，培養(yǎng)推理意識

思維是從疑問和驚奇開始的，教學(xué)過程中，教師要創(chuàng)設(shè)有效的教學(xué)情境，精心合理地設(shè)計(jì)能激發(fā)學(xué)生積極思考的問題，使問題既能夠結(jié)合教材中的知識，又能對學(xué)生的思維發(fā)展具有一定的引領(lǐng)作用，在激發(fā)學(xué)生的推理興趣的同時，讓學(xué)生能夠根據(jù)已有知識，通過歸納與類比等方法推斷出數(shù)學(xué)結(jié)果，從而更好地理解和掌握新知識.例如，在教學(xué)“異分母分?jǐn)?shù)加減法”時，教師可以創(chuàng)設(shè)學(xué)生熟悉的垃圾回收情境.

紙張和廢金屬等是垃圾回收的主要對象，各種垃圾及其比例情況如圖1所示.它們在生活垃圾中共占幾分之幾？

學(xué)生很容易就能列出算式310+14，接著教師就讓學(xué)生想一想怎么算.有的學(xué)生就猜想把分子和分母分別相加，還有的學(xué)生認(rèn)為只要把分子相加.310和14分母不同，這兩種方法顯然不對.這時教師就可以引導(dǎo)學(xué)生回憶，在整數(shù)和小數(shù)加減法中，相同的計(jì)數(shù)單位才能相加減，而分母不相同的分?jǐn)?shù)就是分?jǐn)?shù)單位不相同，學(xué)生很容易就推導(dǎo)出要先通分，把異分母分?jǐn)?shù)轉(zhuǎn)化成同分母分?jǐn)?shù)，這樣分?jǐn)?shù)單位相同了，就可以直接相加減了.這就讓學(xué)生體會到數(shù)的運(yùn)算本質(zhì)上的一致性，培養(yǎng)了他們的運(yùn)算能力和推理意識.

在教學(xué)中，教師充分利用問題情境，引發(fā)學(xué)生的猜想，引導(dǎo)學(xué)生在合作探究中釋疑，不但對所學(xué)知識有所領(lǐng)悟，而且能夠從中找到方法，在新舊知識的類比過程中培養(yǎng)推理意識.

2動手操作，豐富推理過程

有效的推理離不開動手操作，只有加強(qiáng)實(shí)踐操作，才能促進(jìn)學(xué)生推理意識的發(fā)展.在教學(xué)中，教師應(yīng)當(dāng)留給學(xué)生足夠的時間與空間，引導(dǎo)學(xué)生經(jīng)歷觀察、猜想、推理、實(shí)驗(yàn)、驗(yàn)證等活動過程.通過觀察與思考，從實(shí)踐操作上升到抽象思維，引導(dǎo)學(xué)生參與推理的過程，幫助學(xué)生積累推理經(jīng)驗(yàn)，學(xué)會枚舉、歸納等推理方法，進(jìn)而發(fā)展推理意識.

例如，在教學(xué)“三角形的內(nèi)角和是180°”時，教師讓學(xué)生通過量一量、算一算、折一折、拼一拼等不同的方法，尋找三角形內(nèi)角的性質(zhì).活動中，有的學(xué)生利用量角器，量出三角形的三個角的度數(shù)，算出三個內(nèi)角的和，發(fā)現(xiàn)它們的和接近180°；有的學(xué)生把三個角折到一起拼成一個平角；還有的學(xué)生把三個角撕下來拼成一個平角.通過動手操作，學(xué)生很快就推導(dǎo)出了三角形的內(nèi)角和是180°.

操作不能只停留在單純的動手上，更重要的是要通過操作活動撬動學(xué)生思考，教師可以適當(dāng)提問.

師：動手操作是我們探究圖形秘密非常好的辦法，但是操作的過程總是會有一些誤差，三角形的內(nèi)角和確實(shí)是180°嗎？同學(xué)們能不能從數(shù)學(xué)的角度進(jìn)行推理？

生1：從長方形入手，一個長方形有四個直角，內(nèi)角和是360°，分割成兩個直角三角形，每個直角三角形的內(nèi)角和是180°.

生2：有了直角三角形的內(nèi)角和是180°，可以把任意一個銳角三角形沿著其中一條高剪下來，分割成兩個直角三角形，然后把兩個直角三角形的內(nèi)角和減去180°就得到原來銳角三角形的內(nèi)角和，這樣得到所有的銳角三角形的內(nèi)角和都是180°.

生3：用同樣的推理可以得到所有的鈍角三角形的內(nèi)角和都是180°.

生4：三角形按角分類只能分成三類，由此得到所有三角形的內(nèi)角和都是180°.

這個過程中，學(xué)生借助動手操作積累活動經(jīng)驗(yàn)，在小組交流討論的過程中，從特殊出發(fā)，經(jīng)歷從特殊到一般的推理過程.教師把更多的機(jī)會留給學(xué)生，讓學(xué)生面對教師提出的問題，親自動手操作，調(diào)動多種感官參與，引導(dǎo)學(xué)生從動手操作上升到抽象思維，幫助學(xué)生積累推理經(jīng)驗(yàn)，這樣學(xué)生的推理意識與推理能力就能得到很好的發(fā)展.

3制造沖突，激發(fā)推理潛能

推理意識的培養(yǎng)離不開數(shù)學(xué)基礎(chǔ)知識的積累，在有了一定的基礎(chǔ)知識積累后，學(xué)生就能通過觀察、類比、聯(lián)想等數(shù)學(xué)思維活動，不斷地進(jìn)行推理與驗(yàn)證.教師通過對教材的深度挖掘和合理利用，就能更好地激發(fā)學(xué)生的推理潛能，讓學(xué)生的推理意識得到進(jìn)一步的發(fā)展.

例如，在教學(xué)“圓的認(rèn)識”一課中，教師先引導(dǎo)學(xué)生回憶已經(jīng)學(xué)過了哪些平面圖形，然后出示圓，比較它們的不同點(diǎn)，學(xué)生一眼就看出，以前學(xué)過的圖形是由線段圍成的，而圓是由曲線圍成的平面圖形.接著教師再出示橢圓，并提出問題“橢圓也是由曲線圍成的，它是圓嗎”，這就給學(xué)生制造了認(rèn)知沖突.接著教師再引導(dǎo)學(xué)生觀察橢圓的中心點(diǎn)到橢圓的距離不相等，而圓的中心點(diǎn)到圓周的距離相等，還有其他平面圖形的中心點(diǎn)到邊的距離也都不相等.這樣通過觀察、分析、推理，引導(dǎo)學(xué)生概括出圓的本質(zhì)特征：一中同長.

對于新舊知識密切聯(lián)系的內(nèi)容，教師應(yīng)該拓寬教材的深度與廣度，利用學(xué)生已有的知識與經(jīng)驗(yàn)，創(chuàng)設(shè)認(rèn)知沖突，引導(dǎo)學(xué)生去觀察、思考，激發(fā)學(xué)生推理潛能的發(fā)展，促進(jìn)推理意識的提高.

4說理思辨，外顯推理思維

教學(xué)中，教師要有意識地為學(xué)生創(chuàng)設(shè)數(shù)學(xué)表達(dá)的機(jī)會，讓學(xué)生為自己的觀點(diǎn)尋求證據(jù)、應(yīng)對質(zhì)疑，從而促進(jìn)思維的清晰化、條理化，發(fā)展推理意識.教師要善于抓住推理活動的關(guān)鍵環(huán)節(jié)，引導(dǎo)學(xué)生不斷經(jīng)歷“猜想—驗(yàn)證—說理”的過程，讓學(xué)生在有價值的活動中，感悟推理的過程與意義.

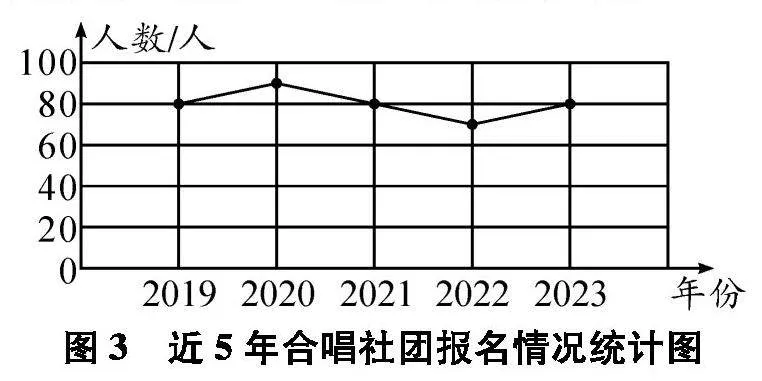
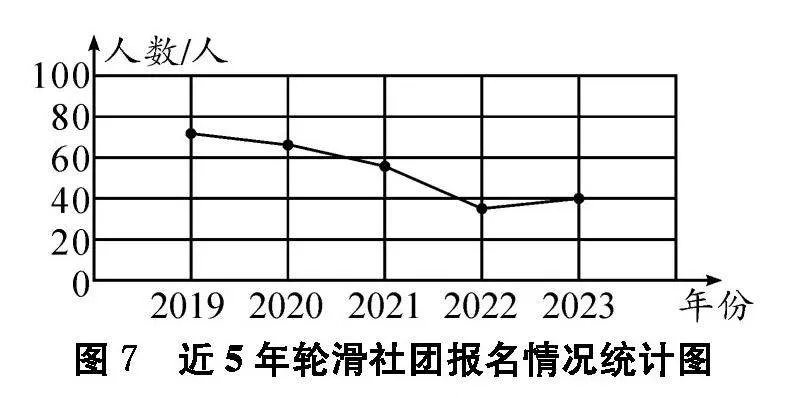
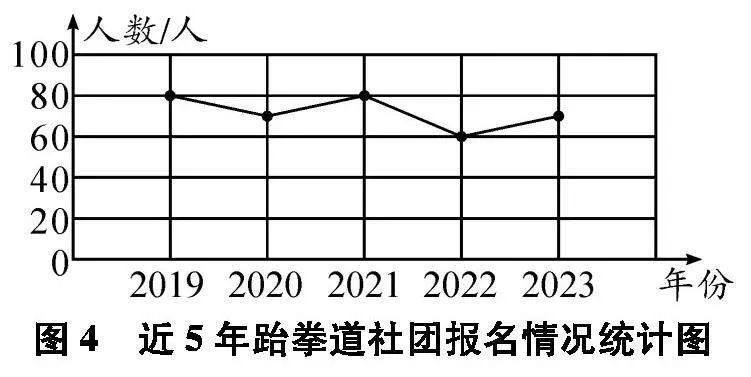
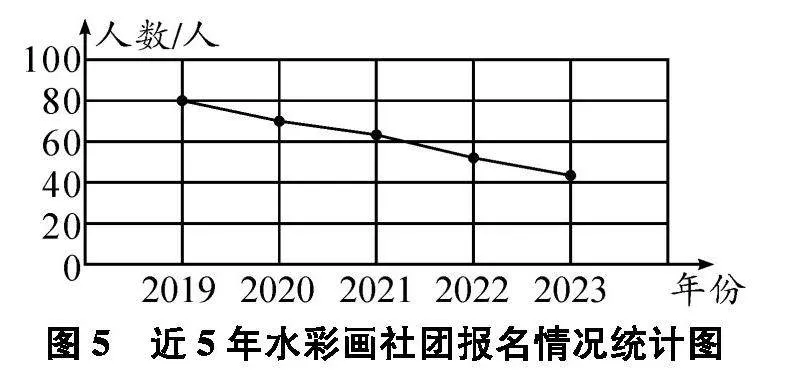
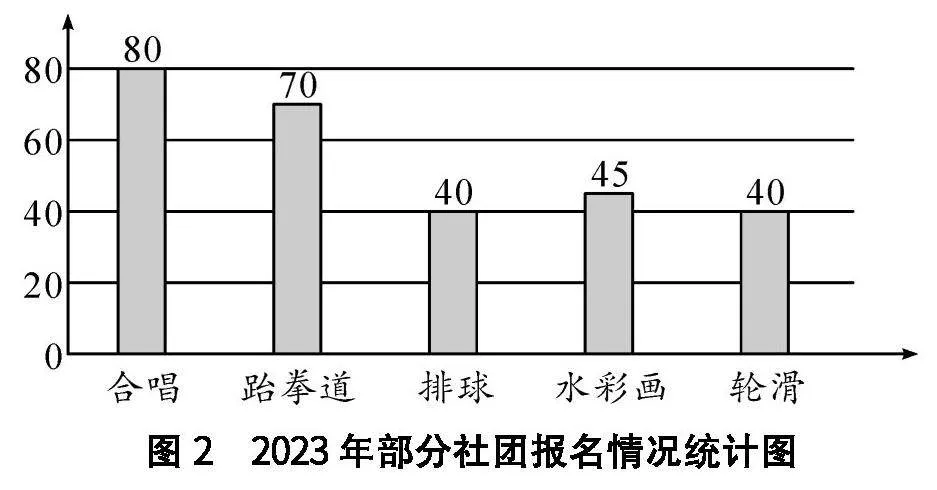
例如，在教學(xué)“折線統(tǒng)計(jì)圖”知識點(diǎn)時，教師可以創(chuàng)設(shè)這樣的問題情境.學(xué)校要精簡一個社團(tuán)，請學(xué)生根據(jù)圖2所示的2023年部分社團(tuán)報名情況統(tǒng)計(jì)圖中的數(shù)據(jù)來選擇精簡一個社團(tuán)，學(xué)生發(fā)現(xiàn)報名人數(shù)最低的排球社團(tuán)和輪滑社團(tuán)都是40人，無法確定精簡掉哪個社團(tuán).

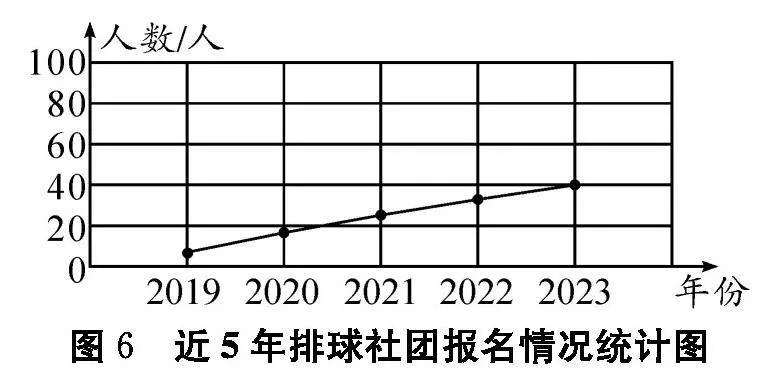
接著教師出示了近5年這5個社團(tuán)的報名人數(shù)情況折線統(tǒng)計(jì)圖（如圖3、圖4、圖5、圖6、圖7）.根據(jù)折線統(tǒng)計(jì)圖中曲線的變化情況，有的學(xué)生認(rèn)為要精簡掉輪滑社團(tuán)，還有的學(xué)生認(rèn)為要精簡掉水彩畫社團(tuán)，因?yàn)樗鼈兌际浅氏陆第厔荩渌鐖F(tuán)報名人數(shù)較多或呈上升趨勢.這樣通過條形統(tǒng)計(jì)圖和折線統(tǒng)計(jì)圖的對比，學(xué)生經(jīng)歷了猜想、辨析、反駁與驗(yàn)證的過程，感悟推理的方法與意義，體會數(shù)學(xué)探索和發(fā)現(xiàn)的樂趣.

學(xué)生說理的過程就是思考的過程，教師在教學(xué)中要給學(xué)生創(chuàng)設(shè)交流與討論的機(jī)會，借助問題引領(lǐng)，適當(dāng)?shù)亟o予點(diǎn)撥、引導(dǎo)，在觀察、實(shí)驗(yàn)、猜想與驗(yàn)證等數(shù)學(xué)活動中，引導(dǎo)學(xué)生逐步養(yǎng)成清晰地表達(dá)自己的思考過程與思考結(jié)果的習(xí)慣，幫助學(xué)生學(xué)會有條理地表達(dá)，有邏輯地思考，讓學(xué)生在不斷思辨中掌握數(shù)學(xué)知識本質(zhì).5結(jié)語

推理意識決定了學(xué)生用數(shù)學(xué)思維思考現(xiàn)實(shí)世界的水平，學(xué)習(xí)數(shù)學(xué)在某種意義上就是學(xué)習(xí)推理.發(fā)展學(xué)生的推理意識，應(yīng)該貫穿小學(xué)數(shù)學(xué)教學(xué)的全過程.教學(xué)過程中，教師要引導(dǎo)學(xué)生“大膽猜想，小心求證”，做到言之有理、言之有據(jù)，這是數(shù)學(xué)推理活動的要求，也體現(xiàn)了數(shù)學(xué)學(xué)科的學(xué)習(xí)特點(diǎn).

參考文獻(xiàn)

［1］中華人民共和國教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)（2022年版）［M］.北京：北京師范大學(xué)出版社，2022.