以不變應(yīng)萬變的二次函數(shù)

摘要：二次函數(shù)是初中數(shù)學(xué)“數(shù)與代數(shù)”部分的重要內(nèi)容.二次函數(shù)的性質(zhì)是解決數(shù)學(xué)問題的基本工具，在不同領(lǐng)域問題解決中具有廣泛應(yīng)用.從存在性問題、動(dòng)點(diǎn)變化到與不同圖形的碰撞融合，二次函數(shù)在解題中展現(xiàn)著自己千變?nèi)f化的魅力.聚焦二次函數(shù)與不同圖形交叉融合的綜合題模型，剖析二次函數(shù)綜合題的求解思路，提高學(xué)生分析問題和解決問題的能力.

關(guān)鍵詞：初中數(shù)學(xué)；二次函數(shù)；圓；平行四邊形；矩形

中圖分類號：G632文獻(xiàn)標(biāo)識碼：A文章編號：1008-0333（2024）26-0033-03

二次函數(shù)是初中數(shù)學(xué)的重要內(nèi)容，是中考數(shù)學(xué)的熱點(diǎn)問題，倍受命題者的青睞.在歷年中考數(shù)學(xué)試題中，它總是以意想不到的方式考查學(xué)生對二次函數(shù)有關(guān)知識的掌握情況.筆者以二次函數(shù)與不同幾何圖形融合的綜合問題為研究對象，探究不同類型問題的解題思路，啟發(fā)學(xué)生靈活運(yùn)用二次函數(shù)知識分析問題和解決問題，以不變應(yīng)萬變.

1二次函數(shù)與圓的綜合性問題

在圓與二次函數(shù)圖象融合的綜合性問題中，教師可啟發(fā)學(xué)生根據(jù)圖形結(jié)構(gòu)特征，充分利用圓的有關(guān)幾何性質(zhì)解決問題［1］.

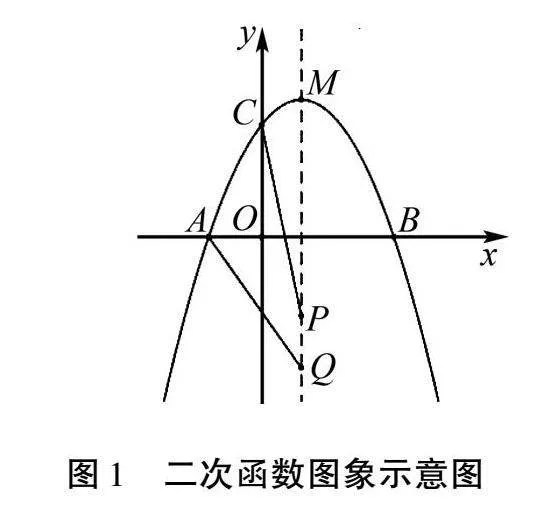
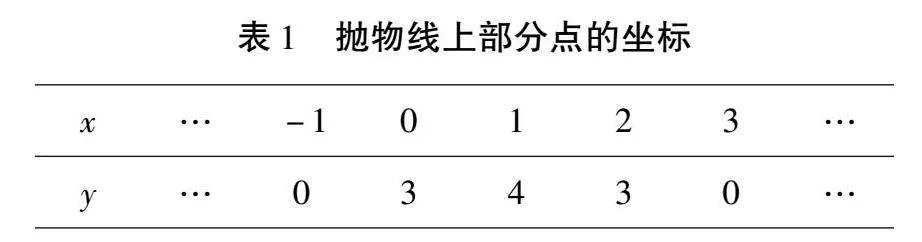
例1如圖1，在平面直角坐標(biāo)系xOy中，拋物線y=ax2+bx+c與x軸分別相交于A、B兩點(diǎn)，與y軸相交于點(diǎn)C，下表給出了這條拋物線上部分點(diǎn)（x，y）的坐標(biāo)值.

（1）求拋物線的解析式及頂點(diǎn)M的坐標(biāo)；

（2）PQ是拋物線對稱軸上長為1的一條動(dòng)線段（點(diǎn)P在點(diǎn)Q上方），求AQ+QP+PC的最小值；

（3）如圖2，點(diǎn)D是第四象限內(nèi)拋物線上一動(dòng)點(diǎn)，過點(diǎn)D作DF⊥x軸，垂足為F，△ABD的外接圓與DF相交于點(diǎn)E，線段EF的長是否為定值？如果是，請求出這個(gè)定值；如果不是，請說明理由.

解析（1）根據(jù)表1給出的拋物線上部分點(diǎn)的坐標(biāo)，利用待定系數(shù)法即可求出解拋物線解析式，這也是求解函數(shù)表達(dá)式常用方法之一.對于拋物線的頂點(diǎn)坐標(biāo)，一方面可利用配方法求解，另一方面可直接利用頂點(diǎn)坐標(biāo)公式求解.由表1可知，A（-1，0），B（3，0），C（0，3）.設(shè)拋物線解析式為y=a（x+1）（x-3），將C（0，3）代入，得3=a（0+1）（0-3），解得a=-1，所以y=-（x+1）（x-3）=-x2+2x+3=-（x-1）2+4.由此可知，拋物線的解析式為y=-x2+2x+3，其頂點(diǎn)坐標(biāo)為M（1，4）.

（2）點(diǎn)P和點(diǎn)Q的位置不確定，點(diǎn)A和C點(diǎn)的位置是確定的，所以需要改變某些點(diǎn)的位置，嘗試尋找三點(diǎn)共線的位置，然后利用“兩點(diǎn)之間，線段最短”解決問題.顯然，需將三條線段之和轉(zhuǎn)化為兩條線段之和，減少不必要的線段.由于線段QP的長度確定，所以可嘗試使得A，Q，C存在三點(diǎn)共線的情形.結(jié)合圖形易發(fā)現(xiàn)，將C點(diǎn)進(jìn)行平移可出現(xiàn)A，Q，C三點(diǎn)共線的情形，故需添加輔助線.

如圖3，將C點(diǎn)沿y軸向下平移1個(gè)單位得到C′0，2，連接BC′交拋物線的對稱軸x=1于點(diǎn)Q′，過點(diǎn)C作CP′∥BC′，交對稱軸于點(diǎn)P′，連接AQ′.因?yàn)殛P(guān)于直線x=1對稱，所以AQ′=BQ′.因?yàn)镃P′//BC′，P′Q′∥CC′，所以四邊形CC′Q′P′是平行四邊形，所以CP′=CQ′，Q′P′=CC′=1.在Rt△BOC′中，BC′=OC′2+OB2=22+32=13.由于A、B點(diǎn)在二次函數(shù)圖象上且處于對稱軸的兩邊，由二次函數(shù)性質(zhì)可知AQ′+Q′P′+P′C=BQ′+C′Q′+Q′P′=BC′+Q′P′=13+1.

（3）如圖4，連接BE，因?yàn)辄c(diǎn)D在二次函數(shù)上，所以可設(shè)D（t，-t2+2t+3），且t＞3.

因?yàn)镋F⊥x軸，所以DF=--t2+2t+3=t2-2t-3.根據(jù)所設(shè)點(diǎn)D的坐標(biāo)可確定點(diǎn)Ft，0，所以BF=OF-OB=t-3，AF=AO+OF=t--1=t+1.因?yàn)樗倪呅蜛BED是圓內(nèi)接四邊形，所以∠DAF+∠BED=180°，又因?yàn)椤螧ED+∠BEF=180°，所以∠DAF=∠BEF.因?yàn)椤螦FD=∠EFB=90°，所以△AFD∽△EFB，所以EFBF=AFDF，即 EFt-3=t+1t2-2t-3，所以EF=t+1t-3t2-2t-3=t2-2t+3t2-2t+3=1，所以線段EF的長為定值1.

點(diǎn)評本題是一道二次函數(shù)與圓的綜合性問題，對于問題（2），其本質(zhì)就是“將軍飲馬”幾何模型，但并不能直接套用模型，需要學(xué)生結(jié)合軸對稱和平移等圖形變換才能解決問題.在解題過程中，找到AQ+QP+PC最小時(shí)點(diǎn)P和點(diǎn)Q的位置也是解題關(guān)鍵.對于問題（3），利用圓內(nèi)接四邊形的性質(zhì)尋找相似三角形，可為問題解決提供簡潔清晰的思路.在解題教學(xué)中，教師一定要注意引導(dǎo)學(xué)生對所學(xué)知識融會貫通，使學(xué)生明白“形”中有“數(shù)”，“數(shù)”中有“形”，為數(shù)形結(jié)合思想運(yùn)用奠定基礎(chǔ).

2二次函數(shù)與平行四邊形的綜合性問題

例2如圖5，已知拋物線y=ax2+bx+4（a≠0）與x軸分別相交于A（1，0）和B兩點(diǎn)，于y軸相交于點(diǎn)C，對稱軸為x=2.5.

（1）求拋物線的解析式；

（2）如圖5，若點(diǎn)P是線段BC上的一個(gè)動(dòng)點(diǎn)（不與點(diǎn)B，C重合），過點(diǎn)P作y軸的平行線交拋物線于點(diǎn)Q，連接OQ，當(dāng)線段PQ長度最大時(shí)，判斷四邊形OCPQ的形狀并說明理由.

（3）如圖6，在（2）的條件下，D是OC的中點(diǎn)，過點(diǎn)Q的直線與拋物線交于點(diǎn)E，且∠DQE=2∠ODQ.在y軸上是否存在點(diǎn)F，使△BEF為等腰三角形？若存在，求F的坐標(biāo)；若不存在，說明理由.

解析（1）因?yàn)閽佄锞€y=ax2+bx+4（a≠0）與x軸交于A（1，0），且對稱軸為x=2.5，從而可得a+b+4=0，-b2a=52，解得a=1，b=-5.故y=x2-5x+4.

（2）由（1）可求得點(diǎn)B，C坐標(biāo).令y=x2-5x+4=0，解得x1=1，x2=4.令x=0，則y=4，所以點(diǎn)B坐標(biāo)為4，0，點(diǎn)C坐標(biāo)為0，4.點(diǎn)P是線段BC上的一個(gè)動(dòng)點(diǎn)（不與點(diǎn)B，C重合），設(shè)直線BC的表達(dá)式為y=kx+t，則t=4，4k+t=0，解得k=-1，t=4.故直線BC的表達(dá)式為y=-x+4.設(shè)點(diǎn)P坐標(biāo)為x，-x+4，則點(diǎn)Q坐標(biāo)為x，x2-5x+4，從而可得PQ=-x+4-x2-5x+4=-x2+4x，故PQ的長度與二次函數(shù)有關(guān).由二次函數(shù)性質(zhì)可知，當(dāng)x=-42×-1=2時(shí)，線段PQ的長度最大，最大值為PQmax=-22+4×2=4，所以點(diǎn)P坐標(biāo)為2，2，點(diǎn)Q坐標(biāo)為2，-2，此時(shí)OC=PQ，由題意可知OC//PQ，故四邊形OCPQ為平行四邊形.

（3）根據(jù)已知條件可直接寫出點(diǎn)D坐標(biāo)為0，2，點(diǎn)Q坐標(biāo)為2，-2，所以直線DQ的表達(dá)式為y=-2x+2.如圖7，過點(diǎn)Q作QH⊥x軸于點(diǎn)H，則QH//CO，故∠AQH=∠ODA.

因?yàn)椤螪QE=2∠ODQ，所以∠HQE=∠HQA，故直線DQ和直線QE關(guān)于直線QH對稱，可設(shè)直線QE的表達(dá)式為y=2x+r，將點(diǎn)D（0，2）代入y=2x+r中，得r=-6，所以直線QE的表達(dá)式為y=2x-6.與二次函數(shù)表達(dá)式聯(lián)立y=x2-5x+4，y=2x-6，解得x=5，y=4.故點(diǎn)E的坐標(biāo)為（5，4），由題意設(shè)點(diǎn)F坐標(biāo)為（0，m），由點(diǎn)B，E的坐標(biāo)可寫出BE2=（5-4）2+（4-0）2=17，要使△BEF為等腰三角形，則存在三種情況：①BE=BF，即16+m2=17，解得m=±1；②BE=EF，即25+（m-4）2=17，方程無解；③BF=EF，即16+m2=25+（m-4）2，解得m=3.125；所以點(diǎn)F的坐標(biāo)為（0，1）或（0，-1）或（0，3.125）.

點(diǎn)評問題（1）是常規(guī)題目，重在考查學(xué)生的基礎(chǔ)知識與基本技能.問題（2）中出現(xiàn)四邊形，目前學(xué)生學(xué)習(xí)過的規(guī)則四邊形數(shù)量有限，可從已知圖形開始嘗試證明，題目中的平行線為解題者提供了思路.因?yàn)樵撍倪呅蔚囊唤M對邊平行，所以可以嘗試證明該四邊形是正方形、矩形、菱形、平行四邊形或梯形.因正方形、矩形、菱形是特殊的平行四邊形且圖象的大致形狀不滿足梯形，所以首先考慮該四邊形是平行四邊形.平行四邊形的證明方法多樣，含有“一組對邊平行”的證明方法有兩種，即“兩組對邊分別平行”或“一組對邊平行且相等”.然后利用二次函數(shù)性質(zhì)可以發(fā)現(xiàn)這一組平行的對邊是相等的，故可證明該四邊形為平行四邊形.問題（3）中學(xué)生需要尋找等腰三角形中三個(gè)點(diǎn)的位置，可以先在題目條件中首先求出確定點(diǎn)的位置，然后假設(shè)不確定點(diǎn)，通過點(diǎn)坐標(biāo)表示線段長度，對不同情形進(jìn)行分類討論，使用這種解題思路，學(xué)生不需要畫圖辨別，只需要通過不同點(diǎn)的數(shù)量關(guān)系就可以求解出結(jié)果.

3結(jié)束語

數(shù)形結(jié)合思想是解決函數(shù)問題的有效工具.它可以幫助學(xué)生利用圖形結(jié)構(gòu)特征直觀解決問題.在解題過程中，使用圖形并不意味著它就可以脫離原本的條件關(guān)系，函數(shù)關(guān)系式就是其中的限制條件.在初中數(shù)學(xué)教學(xué)中，教師需幫助學(xué)生以不變應(yīng)萬變，抓住問題關(guān)鍵，為問題解決創(chuàng)造便利條件.

參考文獻(xiàn)：［1］ 張繼華.數(shù)形結(jié)合解決二次函數(shù)問題［J］.中學(xué)生數(shù)理化（初中版），2023（10）：6-7.

［責(zé)任編輯：李璟］