汽車制動器系統穩定性響應的不確定性和相關性分析

摘要： 在制動噪聲現象中，汽車制動器系統參數不可避免地存在著不確定性和相關性，使得系統響應亦可能同時存在一定的不確定性和相關性，針對該問題開展了制動器系統穩定性響應的不確定性和相關性分析研究。采用多橢球凸模型描述系統參數的不確定性和相關性，以不穩定模態阻尼比表征系統穩定性響應。將多橢球凸模型分別與蒙特卡羅仿真、一階攝動法和二階攝動法相結合，提出了三種系統穩定性響應的不確定性分析方法；結合蒙特卡羅仿真和一階攝動法，分別提出了兩種系統不確定響應的相關性分析方法；基于不確定性和相關性分析方法，提出了建立系統響應橢球域的組合方法。通過算例分析驗證了方法的有效性。分析結果表明，所提出的方法可有效地求得系統穩定性響應的邊界區間、相關系數和橢球域，并且該方法具有較高的計算精度和效率。

關鍵詞： 汽車制動器系統； 多橢球凸模型； 不確定性分析； 相關性分析； 制動噪聲

中圖分類號： U463.51 文獻標志碼： A 文章編號： 1004-4523（2024）09-1546-10

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.011

引 言

汽車制動噪聲與制動器的振動穩定性密切相關，眾多學者主要通過研究系統穩定性來改善制動噪聲問題。受工作條件變化、制造誤差、材料老化等因素的影響，制動器系統的諸多參數往往存在不確定性［1］。因此，研究考慮不確定性的制動器系統穩定性具有重要的工程意義。

近年來，基于不確定性模型的制動器系統穩定性研究受到了越來越多的關注。張立軍等［2］通過考慮制動盤參數的隨機不確定性，采用穩健性設計方法研究了制動尖叫問題。SARROUY等［3?4］基于混沌多項式展開提出了一種不確定性分析方法，用于研究線性制動器系統穩定性問題。NOBARI等［5］引入代理模型研究制動噪聲問題，大大減少了計算時間和成本。黃曉婷等［6］基于模糊模型對制動器的參數不確定性進行建模，提出了一種面向制動噪聲控制的模糊不確定性分析方法。呂輝等［7?8］基于證據理論提出了非精確的概率不確定性分析方法，用于分析制動尖叫問題。

可以看出，基于不確定性模型的制動器系統穩定性研究已經取得較多研究成果。但現有研究還存在如下兩點不足：第一，上述對于制動器穩定性的研究均將系統參數視為相互獨立的不確定變量，沒有考慮不確定參數之間的相關性。然而，在工程實際中，系統不確定參數之間往往存在一定的相關性［9?10］。例如系統制動壓力和摩擦系數之間往往存在相關性。第二，對于實際的工程結構，不僅輸入參數間存在相關性，輸出響應之間也可能存在相關性。當一個響應發生變化，可能會影響其他響應的變化，通過響應相關性分析可以獲得此類影響規律，進而更好地指導后續的優化設計。然而，現有研究很少涉及系統響應的相關性分析。

針對上述可能存在的問題，本文基于多橢球凸模型開展了制動器穩定性響應的不確定性和相關性分析，有針對性地研究了系統不確定參數存在相關性的情形。首先，采用多橢球凸模型描述系統參數的不確定性和相關性；然后，結合蒙特卡羅法、一階攝動法和二階攝動法開展了系統穩定性響應的不確定性分析；接著，結合一階攝動法求解了系統響應的相關性；最后，通過算例驗證了方法的有效性。

1 分析模型

1.1 盤式制動器模型

圖1為一汽車浮動鉗盤式制動器模型［8］，其主要由制動卡鉗、定位銷、支架、制動塊、法蘭盤、制動盤等部件組成。其中，制動盤剛性地連接在輪轂上隨著車輪轉動。制動塊則由襯片底板和摩擦材料組成。系統主要通過制動盤和制動塊間產生的摩擦阻力矩使得汽車減速或停止運動。制動過程中，如果系統處于不穩定狀態，則有可能引發制動噪聲［8］。

制動器系統的振動方程可表示為［1］：

（1）

式中 ，和分別為無摩擦制動器系統的質量、阻尼和剛度矩陣；為摩擦接觸矩陣；為系統振動的廣義位移量，由歐拉公式可得：

（2）

式中 為系統特征值；為振型矩陣。

結合式（1）和（2）可得：

（3）

系統第階的特征值可表示為，其中，和分別表示特征值的實部和虛部。

系統第i階特征值對應的模態阻尼比定義為：

（4）

當為負時，對應的復特征值實部為正，此時系統不穩定，有可能引發制動噪聲。因此，模態阻尼比可以作為評判制動器系統穩定性的指標。

1.2 多橢球凸模型

制動器的諸多不確定參數之間可能存在著一定的相關性。針對該復雜情形，本文引入多橢球凸模型描述系統參數的不確定性和相關性，即將系統參數分為若干組，每組參數用一個單橢球模型描述，組與組之間相互獨立。

假定系統存在n個不確定參數x=（x1 … xi … xn）T，對于任一，記其上界為，下界為，則其中心和半徑定義為：

（5）

的不確定度表示為，方差表示為。

將n個不確定參數分成N組，即 ，。

則不確定參數的中心值也會被分成N組：。

對于，其單橢球凸模型描述為：

（6）

式中 為橢球凸模型的協方差矩陣。

任意兩個不確定變量和的協方差定義為：，其中，為橢圓的旋轉角度。

為剔除參數級大小不同的影響，引入相關系數描述和的相關性：

（7）

不確定參數的協方差矩陣可表示為：

（8）

不確定參數的相關系數矩陣可表示為：

（9）

令，單橢球凸模型也可描述為：

（10）

此時，N組單橢球模型構成的多橢球凸模型為：

（11）

式中 即為描述制動器系統參數的N組單橢球凸模型構成的不確定模型。

2 響應不確定性分析

開展制動器系統模態阻尼比響應的不確定性分析，能獲得響應的上、下邊界。將響應邊界控制在給定的設計范圍內，能有效降低制動噪聲的產生傾向［7］。以表示系統第j個待研究的模態阻尼比，表示系統參數并且采用多橢球凸模型描述。下面給出三種方法用于求解。

2.1 MCUA方法

首先，基于蒙特卡羅仿真［11］提出一種求解的蒙特卡羅不確定性分析（Monte Carlo Uncertainty Analysis，MCUA）方法。MCUA法的主要步驟如下：

（1）根據參數x的相關性，將不確定參數分為N組，，然后構建多橢球凸模型。

（2）假設不確定參數x相互獨立，在范圍內隨機抽取樣本。

（3）將上述樣本代入多橢球凸模型，如滿足模型方程，則將樣本保存；若不滿足，則舍去。

（4）重復步驟（2）和（3），直至獲得組滿足要求的樣本。

（5）計算每一組滿足要求的樣本對應的值，得到個響應值。

（6）選取個響應值中的最大和最小值作為的上、下界，分別記為和，并得到的響應區間。

MCUA的計算精度隨著樣本數量的增大而提高，當抽取樣本數量足夠大時，能獲得相當精確的結果。因此，MCUA可作為參考方法驗證其他分析方法的有效性。

2.2 FPUA方法

MCUA的計算精度嚴重依賴于樣本數量，計算效率往往較低。基于一階攝動法、拉格朗日乘子法和中心差分法提出一種求解的方法。

在處的一階泰勒展開為：

（12）

式中 為的一階偏導數，可表示為：。

采用中心差分法求解偏導數，有：

（13）

式中 為差分步長，且。

，也可被分成N組，，，i=1，2，…，N。

定義的拉格朗日方程為：

（14）

式中 為拉格朗日乘子；結合拉格朗日函數取得極值的必要條件=0以及約束條件，可求得的上、下界分別為：

（15）

（16）

為表述方便，上述方法稱為一階攝動不確定性分析（First?order Perturbation Uncertainty Analysis，FPUA）方法。

2.3 SPUA方法

FPUA適用于不確定度較小或者非線性較弱的情況。為進一步提高計算精度，基于二階攝動法提出一種求解的方法。

基于二階泰勒展開，可表示為：

（17）

式中 為海森矩陣，可表示為：

（18）

忽略的非對角元素，可簡化為：

。

采用中心差分法求二階偏導有：

（19）

根據參數的相關性，也可以分為N組，，其中，，r表示第i組的第r個參數。

的表達式可改寫為：

（20）

以多橢球凸模型為約束，定義第i個拉格朗日函數為：

（21）

存在多個方程累加，考慮第i個橢球凸模型，為非線性方程，此時根據Kuhn?Tucker條件，需要討論以下兩種情況。

（1） 極值點出現在橢球內部時有：

（22）

求解式（22）可得。

（2） 極值點出現在橢球邊界時有：

（23）

求解式（23）可得第二種情形的解。綜合以上兩種情形的解和，記為解集，則存在N組解集。對它們進行排列組合，得最終的解集為。

將這些解代入式（17）得到一系列的值，則的上、下界分別為：

（24）

為表述方便，上述方法稱為二階攝動不確定性分析（Second?order Perturbation Uncertainty Analysis，SPUA）方法。

3 響應相關性及橢球域分析

引入相關系數描述系統任意兩個待研究的模態阻尼比響應和間的相關性。下面將給出兩種方法用于開展系統響應相關性分析，即求解。

3.1 MCCA方法

首先提出一種求解的蒙特卡羅相關性分析（Monte Carlo Correlation Analysis，MCCA）方法。MCCA法的主要步驟如下：

（1）執行MCUA方法的前4個步驟。

（2）計算每一組滿足要求的樣本對應的和值，得到各響應的P個值。

（3）基于各響應的個值，根據定義可以求得各響應的方差和，以及兩個響應間的協方差。進而，可求得兩個響應間的相關系數。

MCCA法計算過程主要基于蒙特卡羅抽樣，計算效率較低。

3.2 FPCA方法

為進一步提高相關性分析效率，基于一階攝動法提出一種求解的方法。

由式（6）可知第i個橢球方程為：

（25）

對橢球方程進行處理，得到：

（26）

僅考慮橢球表面時：

（27）

式中 為單位矩陣。因此，有。即協方差矩陣可表示為：

（28）

得到任意兩個響應的相關系數表達式為：

（29）

等式兩邊同時在不確定域內積分，且N個橢球域都是關于中心對稱的，可得：

因此，兩個響應間的協方差為：

（30）

最后可求得相關系數為：

（31）

為表述方便，上述方法稱為一階攝動相關性分析（First?order Perturbation Correlation Analysis，FPCA）方法。

3.3 橢球域分析

得到任意兩個響應的上、下邊界以及相關系數后，可建立一個橢球域用于量化和的不確定域，其數學表示為：

（32）

式中 為協方差矩陣：

，其中，，，。

根據MCUA和MCCA，可求得和邊界和相關系數，進而建立響應的橢球域。將結合MCUA和MCCA求響應橢球域的方法簡稱為MCUA?MCCA法。類似地，可得到FPUA?FPCA法和SPUA?FPCA法。

4 算例分析

4.1 研究模型

以圖1所示的制動器系統為研究對象，由文獻［8］可知該系統在制動過程中存在的制動噪聲問題。結合文獻［8，12］，選取系統研究參數為：制動盤與制動塊之間的摩擦系數、制動壓力、摩擦材料密度和摩擦材料的楊氏模量。這些參數與摩擦接觸特性緊密相關，在工程實際中表現出較強的不確定性。故將這些參數均視為不確定參數，其取值如表1所示。同時，根據文獻［13?14］可知摩擦系數和制動壓力存在相關性，摩擦材料密度和楊氏模量亦存在一定相關性。

結合文獻［1］可知，在1～16 kHz的范圍內，該模型在7.28和12.9 kHz左右的不穩定模態的阻尼比絕對值較大。因此，選取這兩個模態阻尼比作為主要響應來反映系統的不穩定性。基于有限元分析和響應面法，可建立兩個不穩定模態的阻尼比響應函數，分別記為和：

（33）

（34）

式中 ，并采用多橢球凸模型描述其不確定性和相關性。

兩個響應面模型的決定系數分別為0.9837和0.8932，模型值分別為64.83和17.73，兩模型與有限元模型逼近程度較高，能較好地滿足預測精度要求。

4.2 不確定性分析

考慮系統不確定參數間的相關性，設定相關系數。為分析系統參數不確定性對響應不確定性的影響，以及分析FPUA和SPUA適用的不確定度范圍，給定一系列參數的不確定度，使用不同方法計算響應的邊界，表2和3給出了不同情形下MCUA，FPUA和SPUA的計算結果。其中，MCUA的樣本數為105。

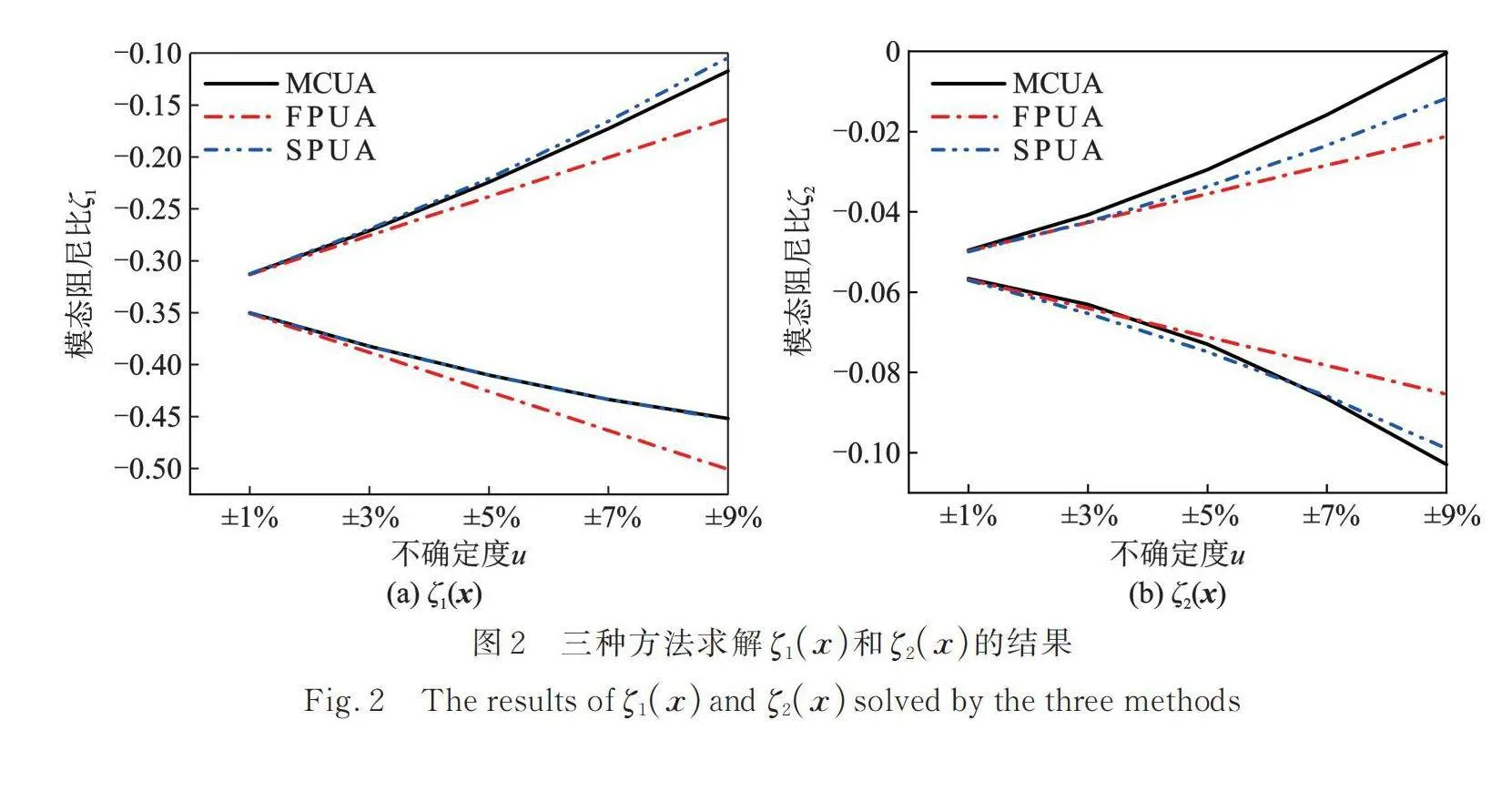
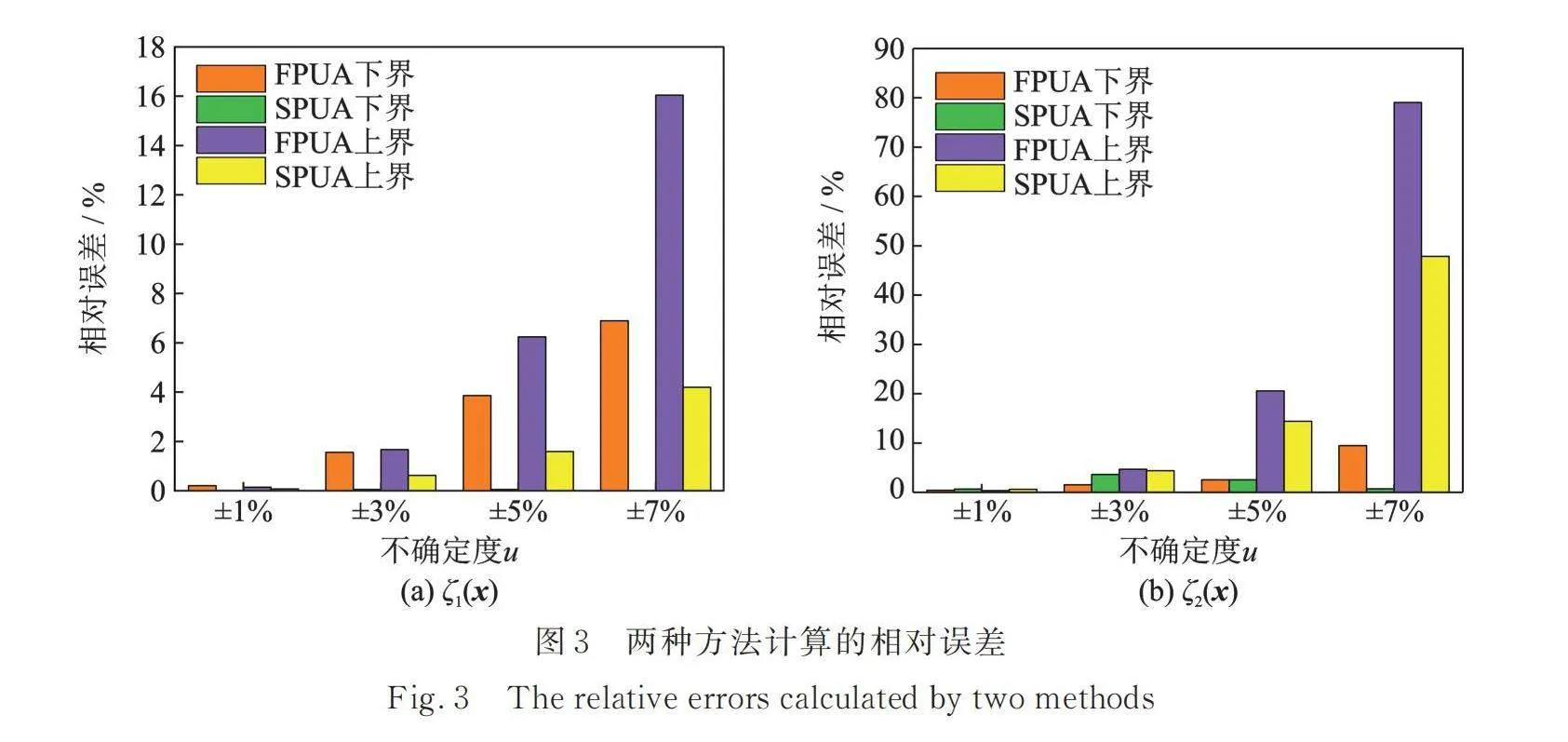
以表2和3為基礎，繪制出MCUA，FPUA和SPUA的計算結果如圖2所示。計算FPUA和SPUA相較于MCUA的相對誤差，如圖3所示。

由圖2可知，和也存在不確定性，且隨參數不確定度增大，和的不確定區間逐漸增大。此外，當時，三種方法的曲線幾乎是重合的，說明此時FPUA和SPUA方法的計算精度均很高；而隨著參數不確定度增大，FPUA和SPUA方法求得的曲線逐漸偏離MCUA求得的參考值曲線，其中FPUA的曲線差異更明顯。在求解的響應時，SPUA方法求得的曲線與參考曲線基本重合。這說明SPUA的計算精度整體上優于FPUA。

由圖3可知，對于下界，當時，FPUA方法計算的相對誤差大于5%，但SPUA方法計算的相對誤差均在5%以內；對于上界，當時，FPUA方法計算的相對誤差超過5%，而SPUA方法計算的相對誤差均在5%以內；對于下界，當時，FPUA的相對誤差超過5%，但SPUA的相對誤差均在5%以內；對于上界，由于其值接近0，兩種方法計算的相對誤差均較大，FPUA方法和SPUA方法均在后相對誤差超過5%。總的來說，SPUA方法的計算精度高于FPUA方法，且適用的不確定度范圍更大。

在計算效率方面，在求解上述響應結果時，MCUA用時48 s，FPUA用時0.25 s，SPUA用時0.4 s。可見FPUA和SPUA在求解系統響應時均具有較高的計算效率。與FPUA相比，SPUA方法的計算效率略低，但大大提高了計算精度。

4.3 相關性分析

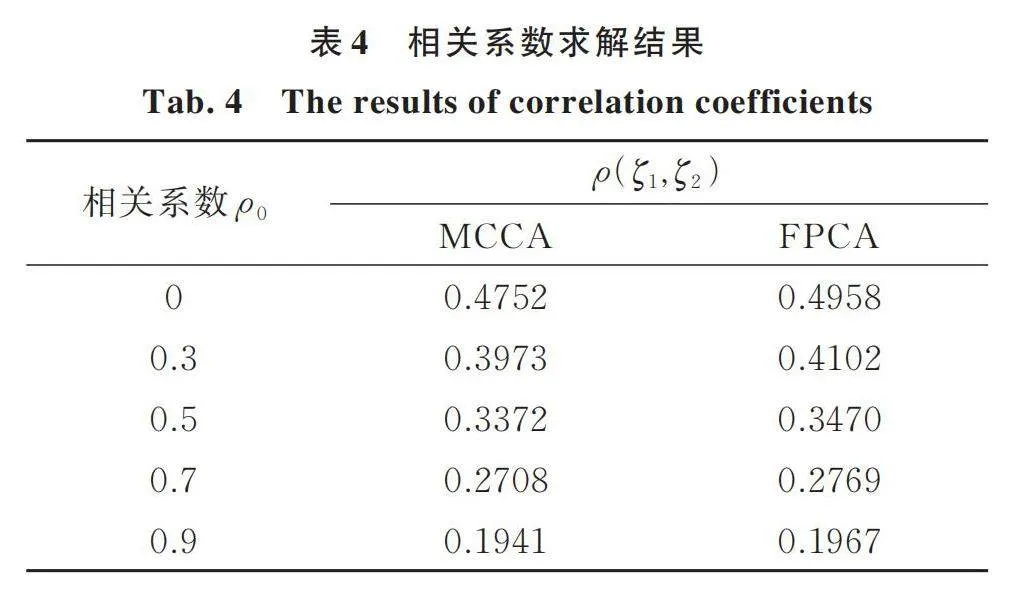
令參數不確定度，分5種情況考慮兩組參數的相關性，即0，0.3，0.5，0.7和0.9。然后分別采用MCCA方法和FPCA方法求解和之間的相關系數，其中，MCCA的樣本數為105，結果如表4所示。以MCCA方法為參考，給出FPCA方法計算的相對誤差，結果如圖4所示。

由表4和圖4可知，以MCCA為參考，FPCA求解響應相關系數的相對誤差均在4.5%以下，兩種方法的計算結果較為接近。此外，還可看出，參數相關性越大時，響應相關性的計算誤差越小。

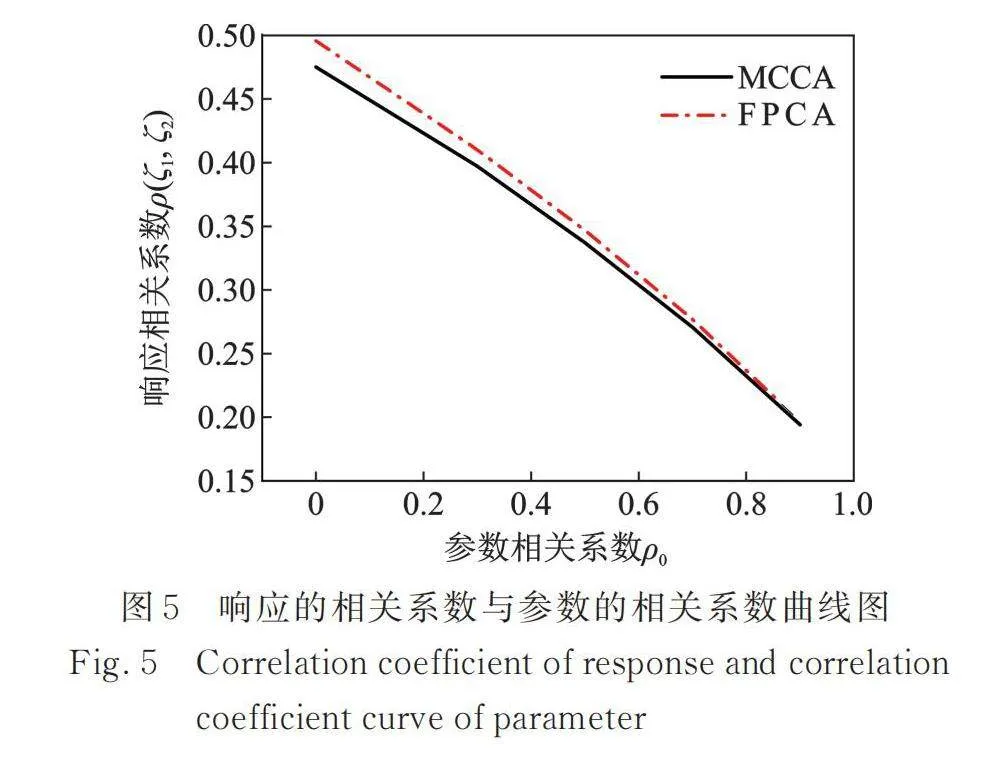
繪制響應的相關系數與參數的相關系數曲線圖，如圖5所示，由圖可見，兩種方法曲線的重合度較高，也體現了FPCA具有較高的計算精度。此外，隨著參數的相關系數逐漸增大，和的相關系數逐漸減小，即兩響應的關聯程度逐漸減弱。

特別地，當系統參數的相關系數為0，即不考慮參數的相關性時，系統響應之間的相關系數并不為0。這表明響應間的相關性不是完全來自系統參數，當參數獨立時，響應間也可能存在相關性。

在計算效率方面，MCCA用時5 s，FPCA用時0.3 s。可見FPCA在求解系統響應相關性時具有很高的計算效率。

綜上，FPCA方法在求解系統響應相關性時具有較高的計算精度和計算效率。

4.4 橢球域分析

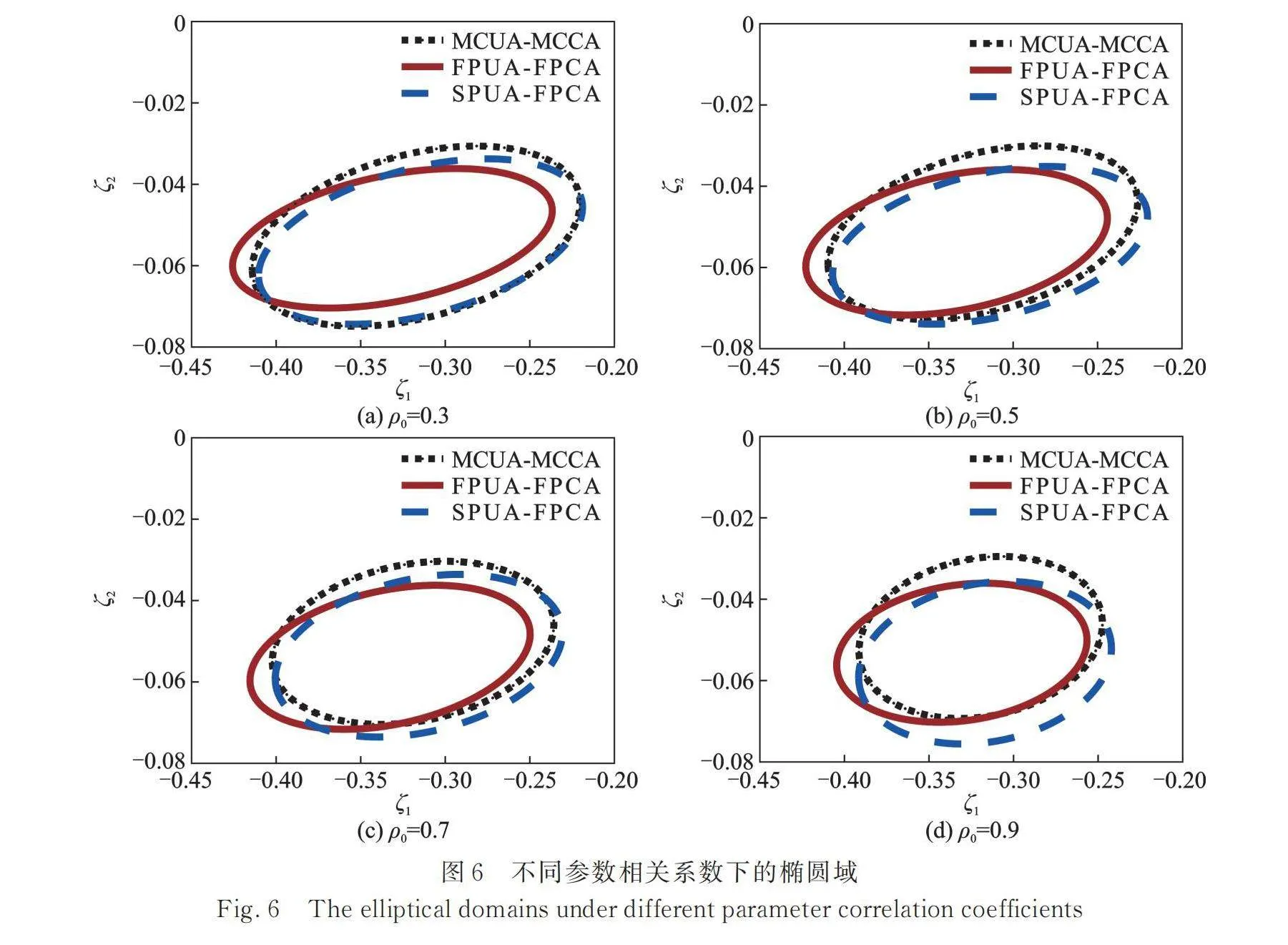
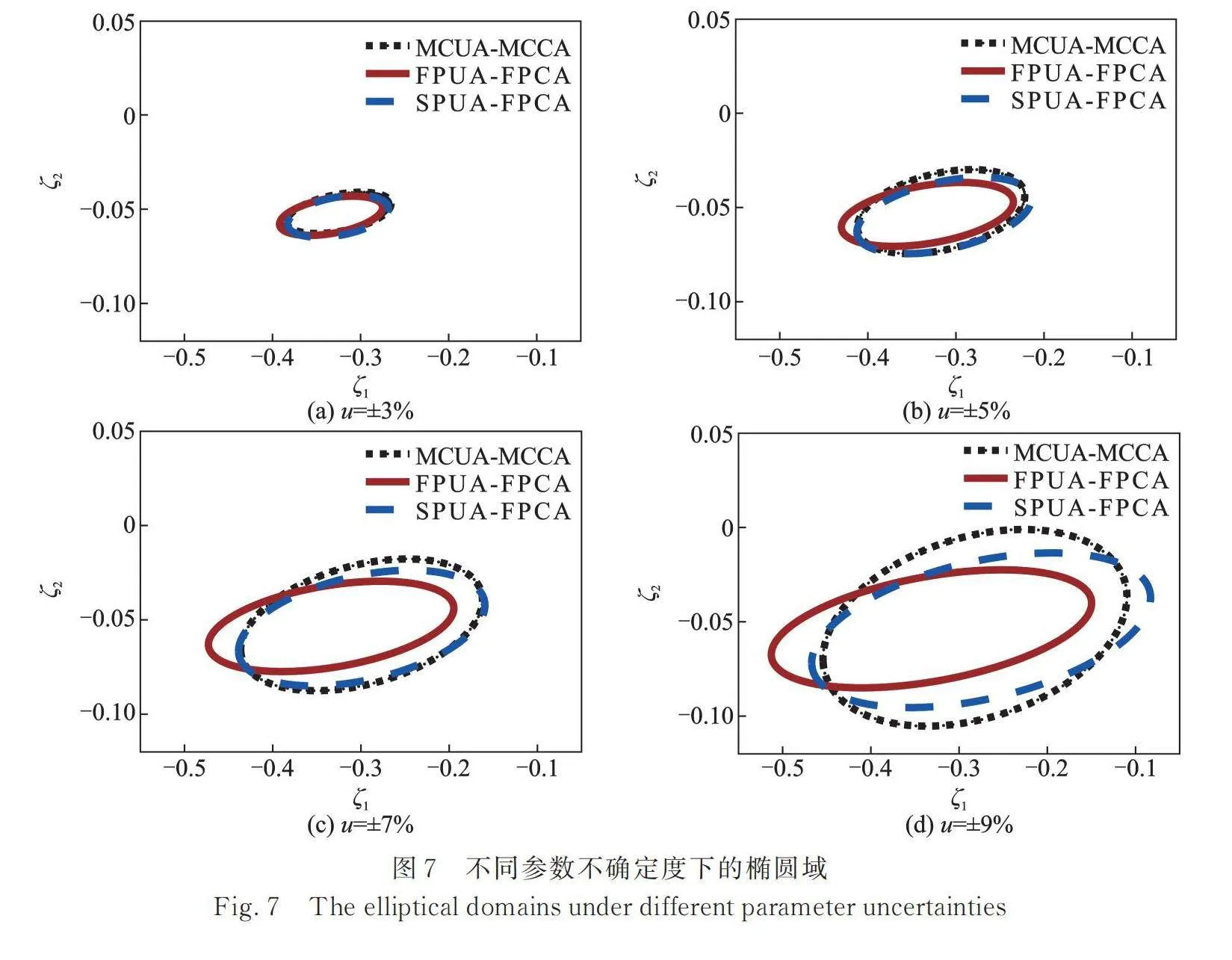
獲得響應的不確定邊界和相關性后，可建立響應的橢球域來直觀反映響應的不確定性和相關性。分別采用MCUA?MCCA，FPUA?FPCA和SPUA? FPCA三種組合方法研究以下兩種情形的響應橢球域：（1）保持參數不確定度不變，改變參數的相關系數取值為0.3，0.5，0.7和0.9，分析結果如圖6所示；（2）保持參數的相關系數不變，改變參數的不確定度為，，和，分析結果如圖7所示。

由圖6可知，以MCUA?MCCA求得的結果為參考，SPUA?FPCA求得的橢圓域比FPUA?FPCA求得的橢圓域更接近參考值，表明SPUA?FPCA的計算結果更為精確。同時，隨著參數相關系數增大，橢圓旋轉角度變小且保持正值，橢圓域逐漸變圓。即響應和的相關系數在減小，正相關程度在降低，這與前文分析一致。

由圖7可知，隨著參數不確定度增大，三種方法求得的橢圓域均增大，橢圓旋轉角度基本不變。說明響應和的不確定范圍在擴大，但正相關性變化不大。此外，FPUA?FPCA和SPUA?FPCA求得的橢圓域隨著參數不確定度增大逐漸偏離參考值，但SPUA?FPCA求得的結果始終接近參考值。這也說明SPUA?FPCA的求解精度更高。

5 結 論

隨著參數不確定度增大，制動器系統穩定性響應的不確定域變大；以MCUA方法作為參考，SPUA方法計算的響應不確定邊界具有更高的精度，且適用于更大的參數不確定度范圍，FPUA方法僅適用于參數不確定度小的情形；FPUA和SPUA方法均具有較高的計算效率。

在求解制動器系統穩定性響應的相關性方面，以MCCA方法為參考，所提出的FPCA方法求得的響應相關系數是有效的，且計算效率更高。

隨著不確定參數相關性增大，所研究的制動器系統兩個穩定性指標響應之間的相關系數減小，正相關性減弱。本文方法亦適用于盤式制動器外的其他類型制動器系統。

參考文獻：

［1］Lü H， YU D J. Brake squeal reduction of vehicle disc brake system with interval parameters by uncertain optimization［J］. Journal of Sound and Vibration， 2014， 333（26）： 7313-7325.

［2］張立軍，龐明，孟德建，等.面向制動尖叫抑制的制動塊穩健性設計［J］.汽車工程，2016，38（1）：65-71.

ZHANG Lijun， PANG Ming， MENG Dejian， et al. Robust design of brake pad for brake squeal suppression［J］. Automobile Engineering， 2016， 38（1）： 65-71.

［3］SARROUY E， DESSOMBZ O， SINOU J J. Piecewise polynomial chaos expansion with an application to brake squeal of a linear brake system［J］. Journal of Sound and Vibration， 2013，332（3）： 577-594.

［4］SARROUY E， DESSOMBZ O， SINOU J J. Stochastic study of a non-linear self-excited system with friction［J］. European Journal of Mechanics-A/Solids， 2013， 40： 1-10.

［5］NOBARI A， OUYANG H， BANNISTER P. Uncertainty quantification of squeal instability via surrogate modelling［J］. Mechanical Systems and Signal Processing， 2015， 60： 887-908.

［6］黃曉婷， 李沛航， 呂輝. 含模糊不確定性的汽車盤式制動器穩定性研究［J］. 重慶理工大學學報（自然科學）， 2021， 35（8）： 48-55.

HUANG Xiaoting， LI Peihang， Lü Hui. Research on the stability of automotive disc brakes with fuzzy uncertainty［J］. Journal of Chongqing University of Technology（Natural Science）， 2021， 35（8）： 48-55.

［7］呂輝， 上官文斌， 于德介. 基于證據理論的汽車制動器系統穩定性分析［J］. 華南理工大學學報（自然科學版）， 2019， 47（3）： 53-60.

Lü Hui， SHANGGUAN Wenbin， YU Dejie. Stability analysis of automotive brake systems based on evidence theory［J］. Journal of South China University of Technology（Natural Science Edition）， 2019， 47（3）： 53-60.

［8］Lü H， SHANGGUAN W B， YU D J. An imprecise probability approach for squeal instability analysis based on evidence theory［J］. Journal of Sound and Vibration， 2017， 387（20）： 96-113.

［9］賈愛芹，陳建軍，徐亞蘭.基于攝動法的不確定性汽車懸架振動控制特征值的凸模型分析［J］.中南大學學報（自然科學版），2012，43（4）： 121-125.

JIA Aiqin， CHEN Jianjun， XU Yalan. Convex model analysis of vibration control eigenvalues of vehicle suspension system based on perturbation method［J］. Journal of Central South University（Science and Technology）， 2012，43（4）： 121-125.

［10］王攀，臧朝平. 改進的平行六面體凸模型識別動力學不確定參數區間的方法［J］. 振動工程學報，2019，32（1）： 97-106.

WANG Pan， ZANG Chaoping. Method of identifying dynamic uncertain parameter intervals with improved parallelepiped convex model［J］. Journal of Vibration Engineering， 2019， 32（1）： 97-106.

［11］CAI B H， SHANGGUAN W B， Lü H， et al. Hybrid uncertainties-based analysis and optimization design of powertrain mounting systems［J］. Science China Technological Sciences， 2020， 63（5）： 838-850.

［12］RENAULT A， MASSA F， LALLEMAND B， et al. Experimental investigations for uncertainty quantification in brake squeal analysis［J］. Journal of Sound and Vibration， 2016， 367： 37-55.

［13］BIJWE J， KUMAR M. Optimization of steel wool contents in non-asbestos organic （NAO） friction composites for best combination of thermal conductivity and tribo-performance［J］. Wear， 2007， 263（7-12）： 1243-1248.

［14］ASHBY M F， CEBON D. Materials selection in mechanical design［J］. Le Journal de Physique Ⅳ， 1993， 3（C7）： C7-1-C7-9.

Uncertainty and correlation analysis for the stability responses of automotive brake systems

Lü Hui1，2， YANG Chao1， SHANGGUAN Wen-bin1， YU De-jie2， ZHAO Ke-gang1

（1.School of Mechanical and Automotive Engineering， South China University of Technology， Guangzhou 510641，China； 2.State Key Laboratory of Advanced Design and Manufacturing for Vehicle， Hunan University， Changsha 410082， China）

Abstract： In the phenomenon of brake noise， the parametric uncertainty and correlation inevitably exist in the automotive brake systems， leading to some uncertainty and correlation of the system response. To address this problem， the uncertainty and correlation analysis for the stability responses of brake systems was carried out. A multi-ellipsoidal convex model was used to depict the uncertainty and correlation of system parameters， and the stability responses of system were characterized by the unstable modal damping ratios. The Monte Carlo simulation， the first-order perturbation method and the second-order perturbation method were respectively combined with the multi-ellipsoidal convex model respectively， and three uncertainty analysis methods of system stability responses were proposed. Based on the Monte Carlo simulation and the first-order perturbation method， two correlation analysis methods of system uncertain responses were developed respectively. The combinatorial methods for establishing the ellipsoid domains of system responses were presented by combining the uncertainty analysis and correlation analysis methods. A numerical example was given to verify the effectiveness of the proposed methods. The analysis results demenstrate that the proposed methods can effectively obtain the boundary intervals， correlation coefficients and ellipsoid domains of system responses， and the methods have high computational accuracy and efficiency.

Key words： automotive brake system；multi-ellipsoid convex model；uncertainty analysis；correlation analysis；brake noise

作者簡介： 呂 輝（1986—），男，博士，副教授。E-mail： melvhui@scut.edu.cn。

通訊作者： 趙克剛（1977—），男，博士，副教授。E-mail： kgzhao@scut.edu.cn。