鉆柱縱-扭耦合非線性振動的頂驅控制研究

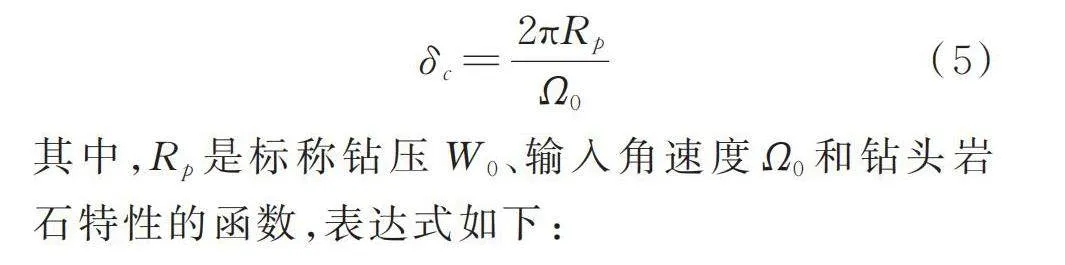
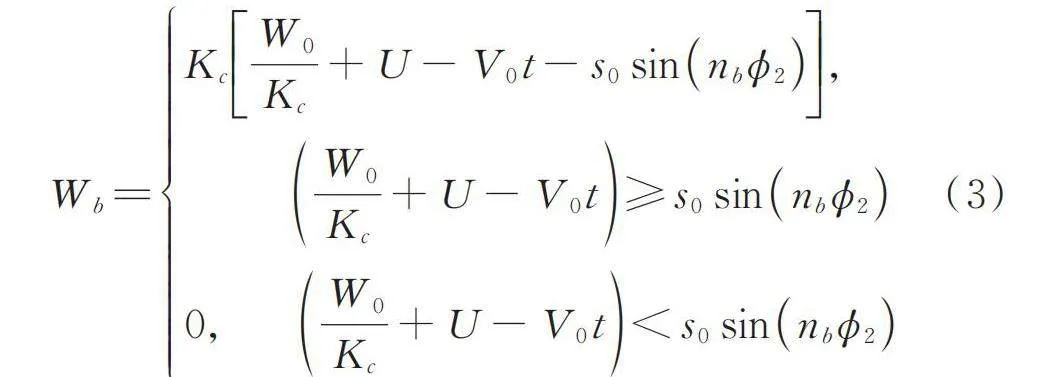
摘要： 本文基于鉆柱縱?扭耦合振動的三自由度集總參數模型，利用數值仿真研究了頂驅控制對鉆柱粘滑振動和跳鉆現象的抑制效果。結果表明，調諧k?c控制對鉆柱振動系統的粘滑振動和跳鉆現象有一定程度的抑制作用，但是在輸入角速度較大而標稱鉆壓較小或者輸入角速度較小而標稱鉆壓較大時的抑制效果并不理想。調諧I?k?c控制可以成功地消除輸入角速度和標稱鉆壓變化對鉆柱粘滑振動和跳鉆現象帶來的影響，使得輸入角速度和標稱鉆壓不論取何值，鉆頭的轉速均穩定在給定的輸入角速度附近，減少了鉆壓、扭矩和軸向位移的波動。

關鍵詞： 非線性振動； 鉆桿縱?扭耦合； 頂驅控制； 粘滑； 跳鉆； 集總參數模型

中圖分類號： O322； TH113.1 文獻標志碼： A 文章編號： 1004?4523（2024）09?1535?11

DOI： 10.16385/j.cnki.issn.1004?4523.2024.09.010

引 言

石油和天然氣等化石燃料是中國重要的基礎性能源，其勘探在很大程度上依賴于鉆井工程［1］。旋轉鉆井是最常用和最具成本效益的油井鉆井技術，鉆柱在其中起著重要作用，它由一系列鉆桿組成，這些鉆桿將動力從頂部的轉盤傳輸到承載鉆鋌和鉆頭的底部鉆具組合［2］。鉆柱的故障會導致整個鉆井作業的關閉，給工程帶來巨大的經濟損失。因此研究鉆柱的動力學行為以避免或減少故障的發生是非常必要的。

鉆柱的振動可分為三類：軸向振動、扭轉振動和橫向振動，劇烈的振動會分別導致跳鉆、粘滑和渦動現象［3］。這些振動模式之間存在著復雜的耦合，為了更好地理解其原理，國內外學者對鉆柱的耦合振動行為進行了廣泛研究［4］。JANSEN等［5］提出一種主動阻尼控制系統，基于扭轉二自由度集總參數模型，以調諧頂驅的方式抑制自激振動。在此基礎上，YIGIT等［6］考慮了軸向振動和扭轉振動的耦合，形成了縱?扭耦合的三自由度模型，模型假設轉臺是由電樞控制的直流電機通過齒輪箱進行驅動，并設計了相應的狀態反饋控制器。ZAMANIAN等［7］首次考慮了轉盤、鉆井泥漿阻尼和主動阻尼控制系統的影響，建立了具有兩個扭轉自由度和一個軸向自由度的縱?扭耦合模型，利用歐拉正向有限差分法求解運動方程，研究了阻尼、主動阻尼比和鉆頭?巖石相互作用次數對粘滑運動的影響。KYLLINGSTAD等［8］介紹了一種粘滑振動控制系統，通過智能控制驅動器來抑制粘滑振蕩。與其他主動振動控制系統相比，該系統不使用任何扭矩反饋，甚至不使用電機，從根本上講該系統是一個PI型速度控制器，可以有效地降低粘滑頻率下的扭轉振動。SARKER等［9］采用集中分段方法將軸向和扭轉各分為21段，建立了鉆柱鍵合圖模型，將頂部驅動電機設定為直流電機，發現采用鉆井行業常用的緩解開環措施可以成功地消除粘滑現象，達到控制鉆柱振動的目的。鞏全成［10］對鉆柱系統粘滑振動建模，通過對鉆柱系統運動方程的分析，揭示了鉆柱粘滑振動的形成機理，建立了基于給定驅動扭矩的粘滑振動控制系統。AL SAIRAFI等［11］建立了包括扭轉和軸向運動的完整驅動系統以及提升系統的四自由度模型，研究表明使用軸向和扭轉控制器可以最大限度地減少粘滑和跳鉆，并保持理想的鉆井條件。韓善凱［12］對鉆桿的非線性振動進行了理論分析及數值仿真，并對鉆柱的粘滑振動進行滑模、PI以及滑模?PI控制研究。張奇志等［13］為了抑制鉆柱粘滑振動和跳鉆現象，基于線性二次型控制策略設計了鉆柱扭轉和軸向狀態的反饋控制器，有效抑制了鉆柱粘滑振動和跳鉆現象。付蒙等［14］基于建立的鉆進系統雙自由度集中參數模型，設計了一種狀態觀測器，可以估計鉆進系統難以測量的井下狀態；并設計了一種參考值優化算法，可以根據鉆頭與巖石間的摩擦扭矩實時計算所有狀態參考值和前饋扭矩輸入量；結合狀態觀測器和參考值優化算法，實現了全維狀態控制器的設計。付蒙等［15］為了抑制鉆柱粘滑振動，提高系統抗干擾能力，建立了鉆柱雙自由度集中參數模型及非線性摩擦擾動模型，設計了一種狀態觀測器，提出了速度補償反饋控制方案。ZHENG等［16］研究了縱?扭耦合動力學的降階模型，該模型考慮了由切削力引起的與干摩擦、脫離接觸和狀態依賴型時滯相關的非線性效應，提出了一種數值延拓方法，構造了分岔圖以捕獲從標稱穩定運行狀態或穩定的無粘滑極限環運動到有粘滑極限環運動的可能途徑，給出了一種基于觀測器的時滯系統控制方案，仿真結果表明該控制器可以有效抑制鉆柱的粘滑行為。張奇志等［17］針對鉆柱的扭轉運動，建立了四自由度鉆柱扭轉模型。為了抑制鉆柱粘滑振動，設計了一種分數階PID控制器。LIU等［18］對文獻［8］的模型做了進一步改進，將用于抑制粘滑振動的機電邊界條件建模為一個可調單自由度系統，將鉆頭處遭受的干摩擦建模為另一個單自由度系統，最后對調諧邊界在典型鉆井系統中的應用進行了數值驗證。

當鉆柱系統工作時，頂驅系統通過自身的旋轉驅動轉盤旋轉，轉盤通過鉆桿來帶動井底鉆具組合，從而實現鉆頭旋轉鉆進。鉆井實踐表明，增大轉盤轉速可一定程度減小粘滑振動現象，但同時產生了軸向振動和橫向振動。鉆井現場調研發現，如果鉆柱長時間處在粘滑振動和跳鉆的狀態下，鉆井設備可能被嚴重損壞，最終導致鉆井失敗［13］。針對鉆柱振動系統存在的粘滑振動和跳鉆問題，已有的研究表明，選擇合適的操作參數可以改善系統的粘滑振動和跳鉆，對于不同的工作情況需要不斷調整，才能找到一組合適的工作參數［13］。因此設計有效的控制方法來抑制鉆柱的粘滑振動和跳鉆問題是必要的。頂驅控制器是鉆柱振動控制研究中最常用的控制器，但在以往的研究中主要用于鉆柱的扭轉振動控制。本文將利用頂驅控制器對鉆柱的縱?扭耦合振動開展控制研究，建立鉆柱振動系統的模型，利用數值仿真研究含頂驅控制器的旋轉鉆井系統在不同的操作條件下的粘滑振動和跳鉆，基于頂驅控制器對鉆柱粘滑振動和跳鉆進行控制。

1 三自由度動力學模型

本節所采用的模型是基于文獻［6］提出的考慮軸向自由度和扭轉自由度耦合的三自由度模型，在此基礎上考慮了文獻［7］提出的頂驅速度控制器，該控制器帶有用于速度、加速度和扭矩控制器的信號延遲濾波器，其線性模型示意圖如圖1所示。圖1中的和分別為輸入角速度和鉆頭的實際轉動角速度，T為來自外部施加的扭矩，R表示反饋增益塊，H_a和H_o分別代表加速度控制器和速度控制器的反饋，H_t代表扭矩控制器的信號延遲濾波器。速度控制器變量P， I和D為輸出軸計算的有效值。對此模型進行了修正，得到如圖1所示的集總參數模型，該模型旨在描述頂部驅動系統產生的機電邊界條件對鉆柱振動響應的影響。

將鉆柱系統的縱向振動和扭轉振動進行分解，其軸向系統結構和扭轉系統結構的簡化模型分別如圖2（a）和（b）所示。在軸向上，將鉆柱建模為彈簧?質量?阻尼系統，縱向剛度和阻尼分別用和表示；鉆桿質量的三分之一和底部鉆具組合（Bottom Hole Assembly， BHA）的組合質量M集中在末端，如圖2（a）所示。在扭轉方向上，頂部驅動被建模為慣性?阻尼?彈簧系統，在實際鉆井工程中，可通過頂部驅動控制器來調整該頂部邊界的參數，這一調整過程通常由可編程控制器（PLC）控制的變頻驅動系統來實現，控制器采用了比例（P）、積分（I）和微分（D）控制策略；來源于PID速度控制器的I因子，來源于控制器的P因子，而來源于控制器的D因子，在頂驅控制系統中，和可以通過變頻調速進行控制，為了保持系統的穩定，和應該始終不小于0；為了抵消頂驅巨大的轉動慣量，應為負值［19］。除了頂部驅動外，鉆柱被建模為集總慣性?阻尼?彈簧系統，如圖2（b）所示。

根據牛頓第二定律，鉆柱系統的運動方程可寫作［6］：

（1）

式中 U表示鉆頭的軸向位移；表示軸向進給速度；M表示鉆桿質量的三分之一和BHA的組合質量［10］；和分別表示鉆桿系統的縱向剛度和阻尼；為標稱鉆壓（其值為鉆柱系統的重力減去頂部鉤載與鉆柱所受浮力的和）；（Weight?On?Bit，WOB）和（Torque?On?Bit，TOB）分別為鉆柱工作時鉆頭與巖石相互作用的合力和合力矩；為頂驅的角位置變量；為鉆頭在井底的角位置變量；需要注意的是，不是頂部驅動的轉速，而是輸入到速度控制器的標稱轉速；和分別為鉆桿系統的扭轉剛度和阻尼，和分別為來自速度控制器的積分因子和比例因子。轉動慣量和的表達式如下：

（2）

式中 為速度控制器的微分因子；，，和分別表示鉆桿、鉆鋌、鉆頭和頂驅的轉動慣量［18］。

在式（1）中，的數學表達式如下［5］：

（3）

式中 為地層接觸剛度；為初始切削深度。本文選（對應PDC鉆頭）。鉆頭上的扭矩可由鉆壓、鉆頭半徑、摩擦函數和切削深度獲得，可表示為：

（4）

其中，由鉆頭的類型決定；切削深度可由機械鉆速（Rate?Of?Penetration，ROP）表示：

（5）

其中，是標稱鉆壓、輸入角速度和鉆頭巖石特性的函數，表達式如下：

（6）

其中，和表征了鉆頭的摩擦過程和切削作用，取決于鉆頭類型。

式（4）中的摩擦函數描述鉆頭與地層之間的摩擦行為，是鉆頭轉速的非線性函數，表達式如下［20］：

（7）

式中 代表最大靜摩擦力（矩）調節系數；為動摩擦力（矩）調節系數。

2 數值仿真

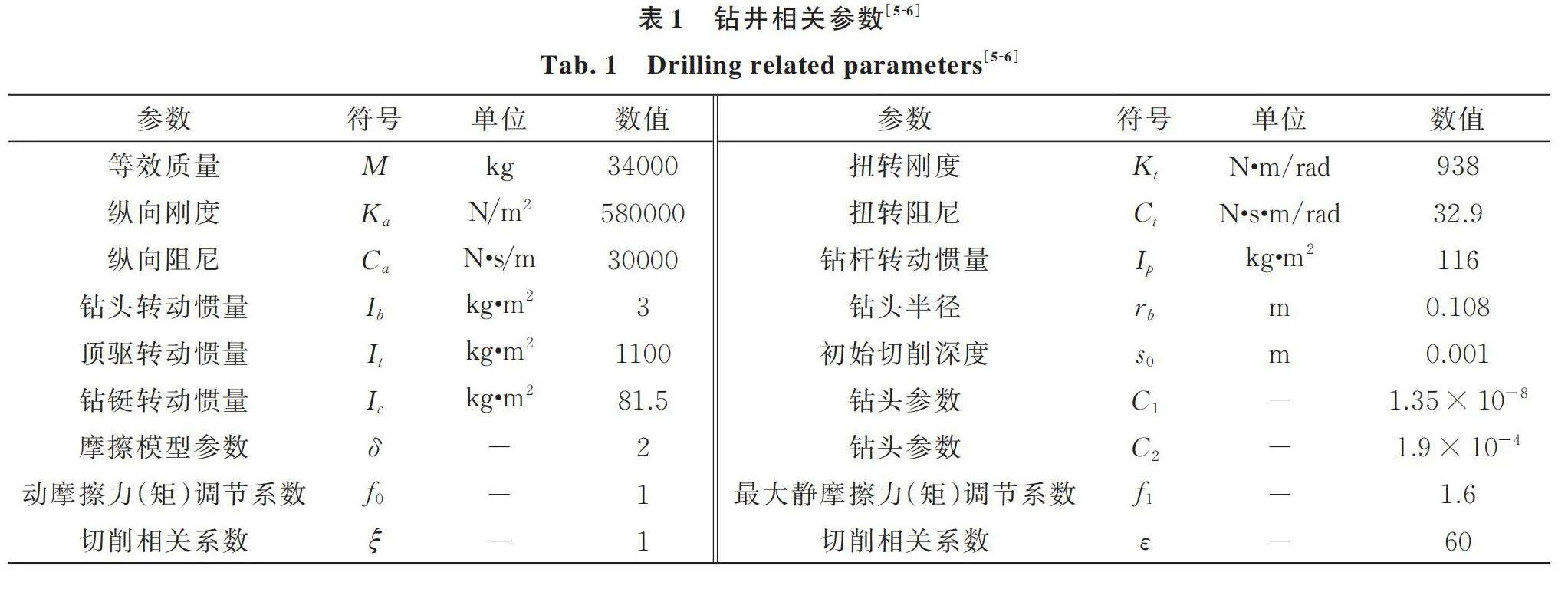
在構建鉆柱運動系統仿真模型前，必須選擇適當的鉆柱系統參數。根據文獻［5?6］，鉆柱軸向和扭轉振動系統及鉆頭?巖石相互作用的相關仿真參數如表1所示。頂驅控制器的控制參數取自文獻［18］的數據，因為該頂驅控制器施加在扭轉方向上，通過鉆頭?巖石相互作用模型與軸向進行耦合，從而達到控制軸向振動的目的，因此文獻［18］中的控制參數在本文中依舊適用，表2列出了相關的參數。

2.1 頂驅控制器對鉆柱系統響應的影響

為了方便討論鉆井的工作參數和頂驅控制器對鉆柱振動系統響應的影響，本小節首先在原始剛性邊界條件下，在給定鉆壓，改變輸入角速度和給定輸入角速度，改變鉆壓兩種情況下分析研究鉆柱振動系統的響應情況，并初步針對頂驅控制器對鉆柱振動系統控制前后的仿真結果進行對比分析。

2.1.1 剛性邊界條件下鉆柱系統參數變化對系統響應的影響

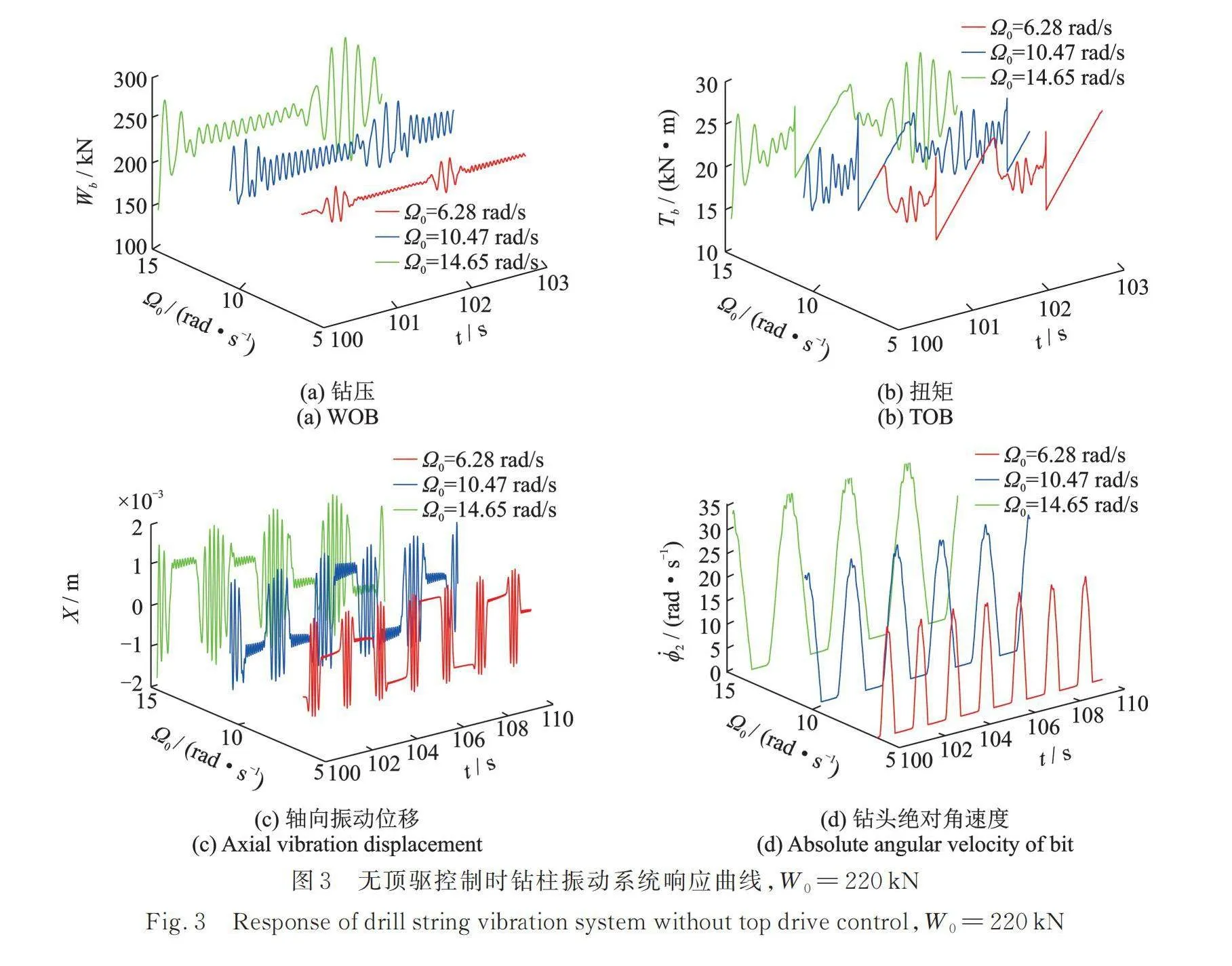
（a）保持不變，增大

在給定標稱鉆壓=220 kN，輸入角速度變化時，鉆柱振動系統在控制前的剛性邊界條件下的響應曲線如圖3所示。從圖3可以看出，隨著輸入角速度的增大，鉆壓、扭矩、鉆頭角速度和軸向振動位移X的響應波動幅值均有所增加，但鉆頭的黏滯時間隨著轉速的增大逐漸減小。表3給出了不同輸入角速度下鉆頭發生黏滯現象的持續時間。在輸入角速度分別為6.28，10.47和14.65 rad/s時，鉆柱振動系統發生粘滑現象，黏滯時間分別為0.93，0.78和0.65 s，這表明提高驅動角速度可以減小粘滑振動；但是隨著輸入角速度的增加，在軸向進給速度恒定（ ）的情況下，鉆頭的軸向振動位移由1.2 mm增加至1.6 mm，鉆壓由242 kN增加到了290.5 kN，這說明提升輸入角速度會導致軸向振動的加劇。

（b） 保持不變，增大

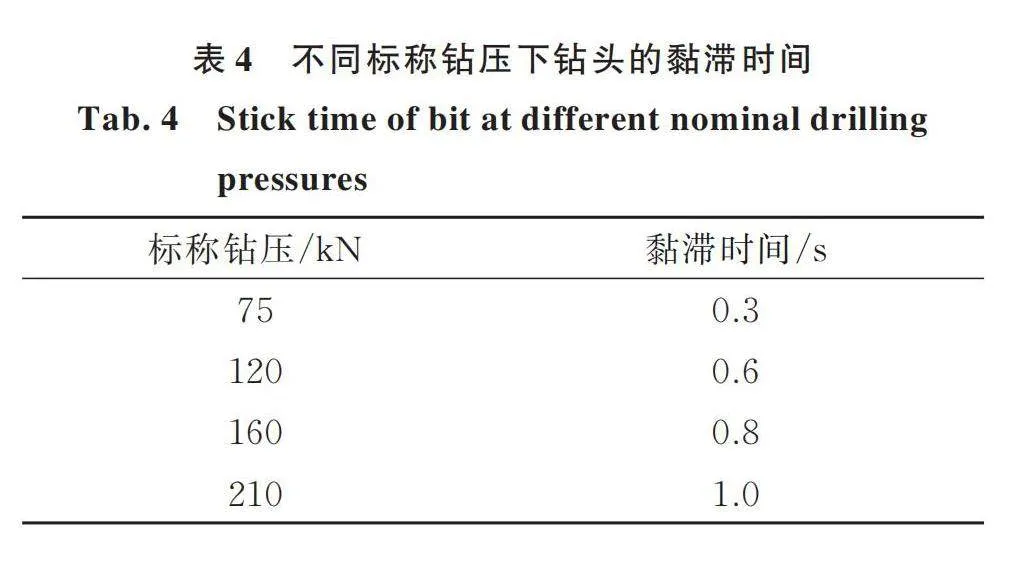
在給定輸入角速度=10.47 rad/s，標稱鉆壓變化時，鉆柱振動系統在控制前的剛性邊界條件下的響應曲線如圖4所示。從圖4可以觀察到，隨著標稱鉆壓的增大，鉆壓的響應波動范圍增大了55%，扭矩的波動范圍增大了71.04%。從表4給出的不同標稱鉆壓下鉆頭發生黏滯現象的持續時間可以看出，鉆頭的黏滯時間由0.3 s增大到1 s，這些現象表明增大標稱鉆壓會導致鉆柱粘滑振動現象的加劇。

仿真結果表明，增大輸入角速度或者減小鉆壓可一定程度減小粘滑振動現象，但同時會導致軸向振動的加劇，并且對粘滑振動的抑制效果并不理想。因此，必須設計有效的控制器來控制鉆柱的粘滑振動和跳鉆現象。接下來討論當輸入角速度和鉆壓給定時，頂驅控制器對鉆柱振動系統控制前后的差異。

2.1.2 頂驅控制對鉆柱系統響應的影響

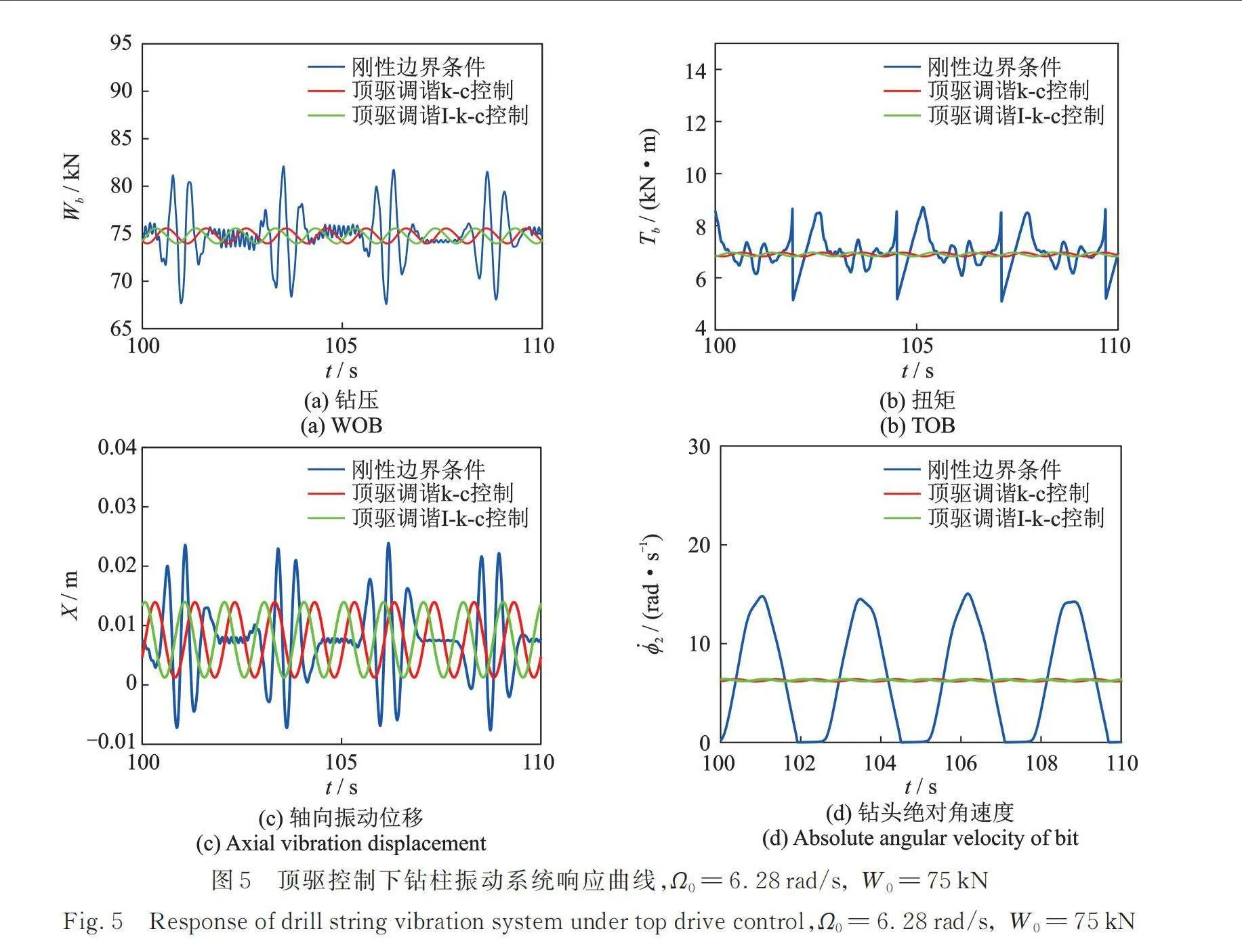
在給定輸入角速度和標稱鉆壓為6.28 rad/s和75 kN時，鉆柱振動系統的響應曲線如圖5所示。從圖5可以看出鉆壓和扭矩在頂驅控制器調諧控制前后均不為零，表明鉆柱系統在控制前和控制后鉆頭與底層接觸穩定，沒有跳鉆現象。但相較于控制前的剛性邊界條件，可以發現經過頂驅控制器調諧控制后，鉆頭上施加的鉆壓在75 kN附近波動，響應波動范圍明顯縮小；扭矩的響應波動范圍也有所減小，在7 kN·m附近略有波動。在圖3（d）中，鉆柱振動系統在控制前的剛性邊界條件下，鉆頭角速度的波動范圍為0～14.8 rad/s，波動較大，并且鉆頭絕對角速度出現了的現象。選取仿真時間為的系統響應曲線分析發現，鉆頭角速度完整波形先是減小至0（黏滯階段），然后繼續下放鉆頭，直到在旋轉方向達到非常高的速度14.8 rad/s（滑脫階段），如此反復循環。經過頂驅控制器調諧控制之后可以觀察到，不管是頂驅控制器調諧k?c控制還是調諧I?k?c控制，在系統響應穩定之后，鉆頭角速度均在輸入角速度附近略有波動。與控制前相比較可以發現，鉆柱粘滑振動現象被消除，軸向振動降低到非常低的水平。

從圖5可以看出，在給定工作參數和分別為6.28 rad/s和75 kN時，頂驅調諧k?c和I?k?c控制后的效果基本一致。為了比較兩種控制策略的差異，接下來針對工作參數變化時，不同控制策略對粘滑振動和跳鉆現象的控制效果進行對比分析。

2.2 頂部調諧控制對粘滑振動的影響

2.2.1 調諧k?c對鉆柱系統粘滑振動的影響

在給定標稱鉆壓=220 kN，輸入角速度變化時，經過頂驅控制器調諧k?c控制后的鉆柱振動系統響應曲線如圖6所示。與圖3相比較可以發現，對于低轉速6.28和10.47 rad/s，頂驅控制器調諧k?c的控制效果比較差，但是當輸入角速度為14.65 rad/s時，調諧k?c控制對其控制效果良好，控制后的鉆頭角速度在輸入角速度附近略有波動，鉆柱振動系統的鉆壓在標稱鉆壓附近略有波動。

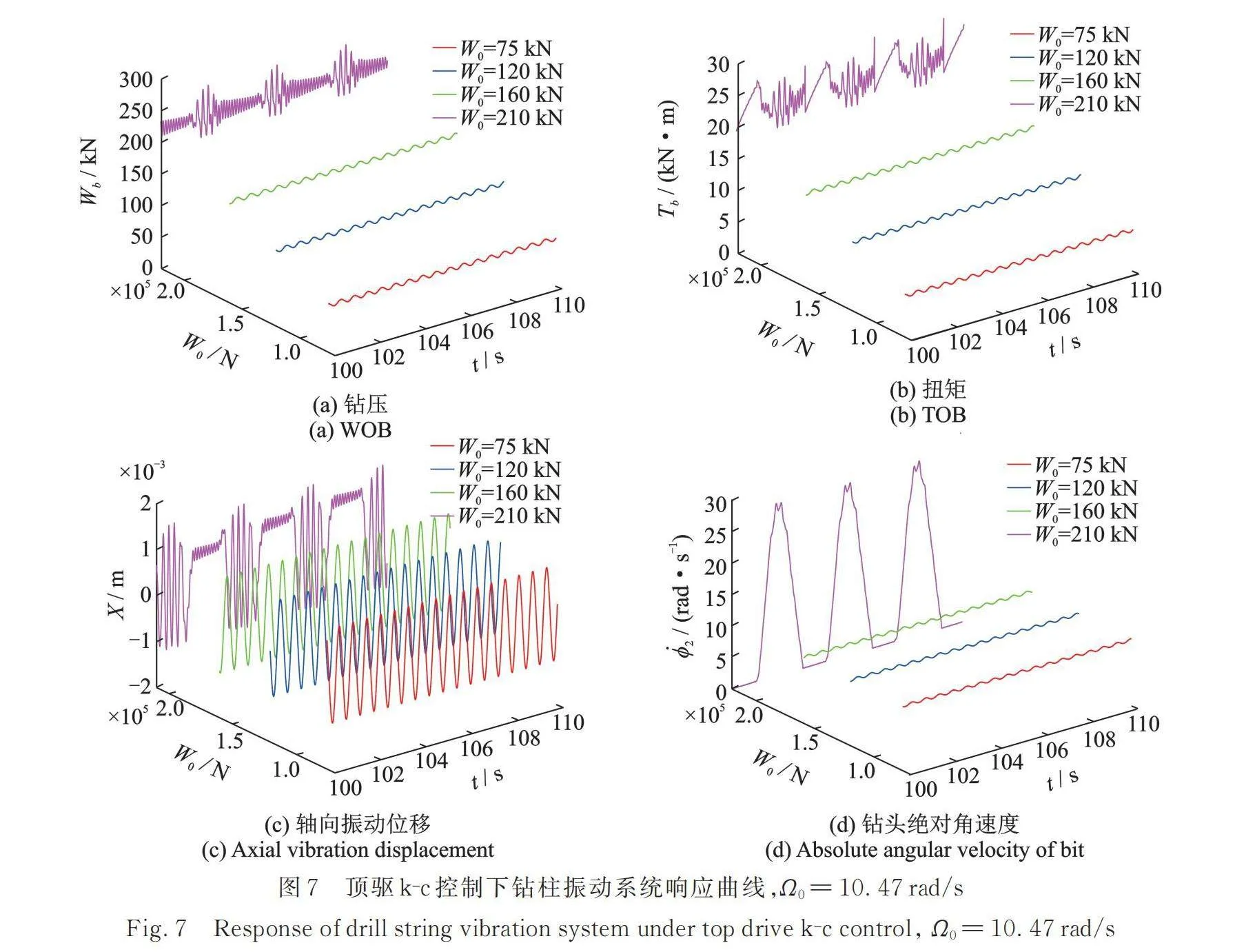
在給定輸入角速度=10.47 rad/s，標稱鉆壓變化時，經過頂驅控制器調諧k?c控制后的鉆柱振動系統響應曲線如圖7所示。與圖4相比較可以觀察到，頂驅控制器調諧k?c控制對低鉆壓的控制效果比較好；但當標稱鉆壓時，鉆柱振動系統仍處于粘滑振動中。

不難看出，頂驅控制器調諧k?c對于標稱鉆壓較高而輸入角速度較低，或者標稱鉆壓較低而輸入角速度較高時系統出現的粘滑振動控制情況并不理想。

2.2.2 調諧I?k?c對鉆柱系統粘滑振動的影響

在給定標稱鉆壓=220 kN，輸入角速度變化時，經過頂驅控制器調諧I?k?c控制后的鉆柱振動系統響應曲線如圖8所示。與圖6比較可以發現，當輸入角速度為6.28和10.47 rad/s時，鉆壓、扭矩、鉆頭角速度和鉆頭的軸向振動位移X的響應波動幅值明顯減小。當輸入角速度為10.47 rad/s時，控制后鉆壓、扭矩和軸向振動位移的最大幅值分別降低為Wbmax=230 kN（降低了21%），Tbmax=22 kN·m（降低了20.3%）和Xmax=1.01 mm（降低了35.3%），而控制前的值分別為290.5 kN，27.9 kN·m和1.56 mm（見圖3）。

表5給出了不同控制情況和不同輸入角速度下的最大鉆壓。由表5發現在剛性邊界條件下，鉆壓的最大值在逐漸增大，表明鉆頭與地層接觸不穩定；但經過調諧I?k?c控制之后，鉆壓的最大值穩定在標稱鉆壓附近，說明在剛性邊界條件下鉆柱劇烈的縱向振動經過頂驅控制器調節之后得到了良好的控制。

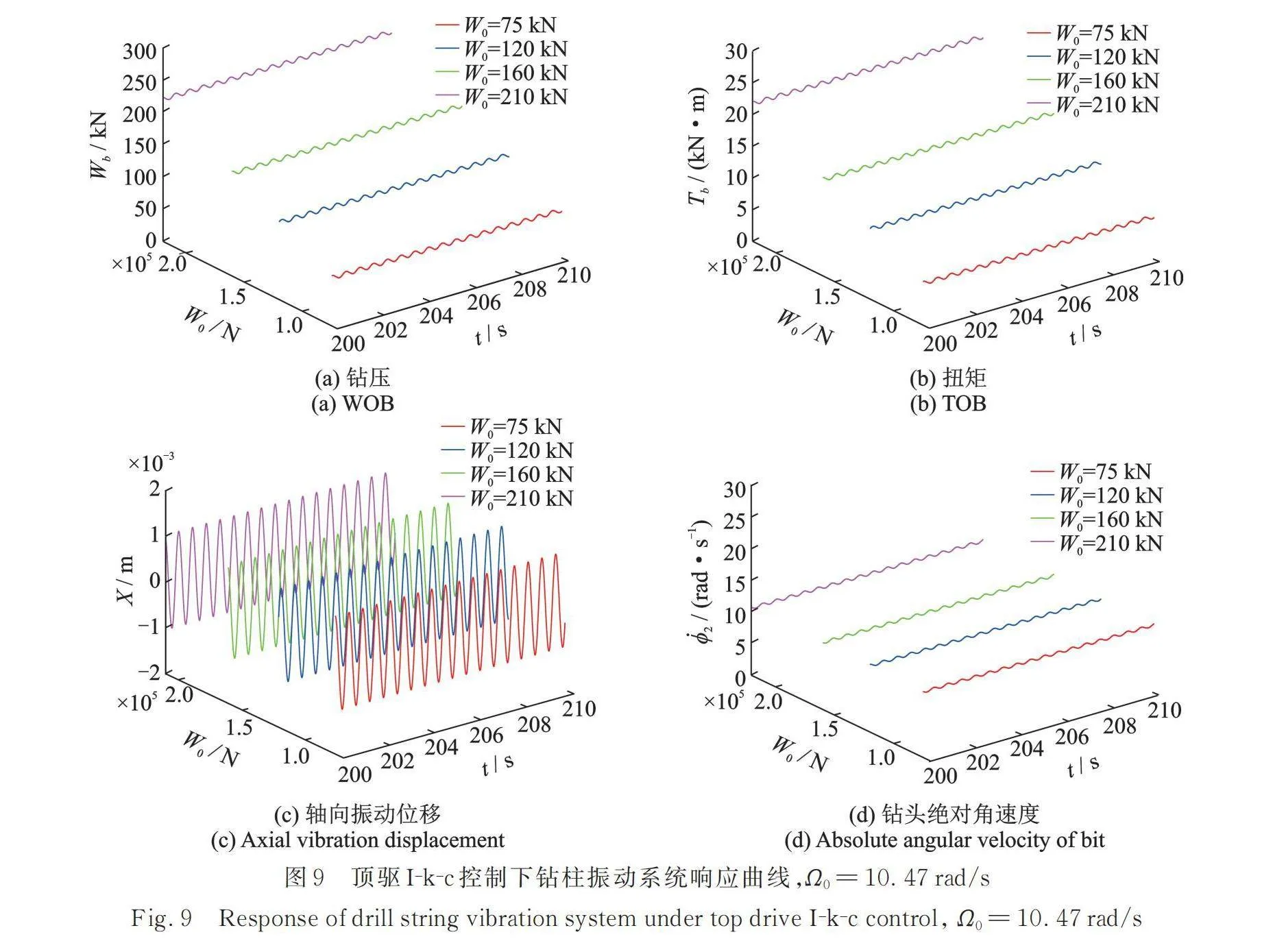
在給定輸入角速度=10.47 rad/s，標稱鉆壓變化時，經過頂驅控制器調諧I?k?c控制后的鉆柱振動系統響應曲線如圖9所示。與圖7相比較可以發現，當標稱鉆壓為210 kN時，鉆壓、扭矩、鉆頭角速度和鉆頭的軸向振動位移X的波動幅值均得到了明顯的控制，相比較于圖7，，和分別降低了62.7%，23%和26.5%，鉆柱振動系統的粘滑運動完全消失。

表6給出了不同控制情況和不同標稱鉆壓下的最大鉆壓。可以發現相比與頂驅調諧k?c控制，頂驅調諧I?k?c控制對于輸入角速度較低，而標稱鉆壓較高時系統的振動響應控制效果更好，其更能消除工作參數變化對于系統穩定性的影響，而頂驅調諧k?c控制只是增加了系統穩定運行的參數范圍。

2.3 頂部調諧控制對跳鉆的影響

2.3.1 調諧k?c對鉆柱系統跳鉆的影響

在給定標稱鉆壓=75 kN，輸入角速度變化時，經過頂驅控制器調諧k?c控制后的鉆柱振動系統響應曲線如圖10所示。可以觀察到，高轉速30.3和33.49 rad/s時，調諧k?c控制對其控制效果比較差，鉆柱振動系統仍有跳鉆現象存在；但是當輸入角速度為25.12 rad/s時，頂驅控制器調諧k?c的控制效果比較好，鉆柱振動系統的跳鉆現象被消除。

2.3.2 調諧I?k?c對鉆柱系統跳鉆的影響

在給定標稱鉆壓=75 kN，輸入角速度變化時，經過頂驅控制器調諧I?k?c控制后的鉆柱振動系統響應曲線如圖11所示。與圖10比較可以發現，當輸入角速度為30.35和33.49 rad/s時，鉆壓、扭矩、鉆頭角速度和鉆頭的軸向振動位移X的波動幅值明顯減小。當角速度為33.49 rad/s時，控制前的鉆壓、扭矩和軸向振動位移的最大幅值分別為403.9 kN， 46.5 kN·m和7.3 mm，而控制后則分別降到了132.9 kN（降低了67%），25 kN·m（降低了46%）和1.3 mm（降低了82.3%）。

表7給出了不同控制情況和不同輸入角速度下的最大鉆壓。由表7發現經過調諧I?k?c控制之后系統鉆壓的最大值盡管隨著輸入角速度的增大也有所增加，但依舊遠遠小于剛性邊界條件下的系統最大鉆壓，且當輸入角速度分別為30.35和33.49 rad/s時，相比于調諧k?c控制，調諧I?k?c控制對鉆壓的控制效果更好。

綜上所述，鉆柱粘滑振動問題和跳鉆現象可以通過頂驅調諧I?k?c控制得到有效抑制。

3 結 論

本文在傳統的二自由度集總參數模型上，增加了頂驅控制器，基于準靜態的鉆頭?巖石相互作用模型，建立了一個縱?扭耦合三自由度集總參數模型；該頂驅控制器實際上是一個PID型驅動速度控制器，可通過調節增益因子對鉆柱振動進行控制。

仿真結果表明，系統在控制前的剛性邊界條件下隨著標稱鉆壓的增加，鉆頭的黏滯時間逐漸延長，隨著輸入角速度的增加，鉆頭的黏滯時間慢慢減短；但是當輸入角速度過大時，鉆柱振動系統出現了跳鉆現象，且隨著輸入角速度的增大，鉆頭的跳鉆時間逐漸延長；這些現象表明增大輸入角速度或減小標稱鉆壓可一定程度抑制鉆柱的黏滑運動現象，但會導致軸向振動加劇，過大的輸入角速度甚至會導致鉆柱振動系統出現跳鉆現象。

將兩種不同控制策略的仿真結果進行比較可以發現，在施加頂驅控制器調諧k?c控制后，當標稱鉆壓較高、輸入角速度也相對較大時，調諧k?c對粘滑振動的控制效果比較好；在標稱鉆壓較小、輸入角速度也相對較小時，調諧k?c對跳鉆現象的控制效果較為明顯；即標稱鉆壓和輸入角速度均相對較大或者相對較小時，頂驅控制器調諧k?c控制對鉆柱的粘滑振動和跳鉆現象才會有明顯的控制效果。而施加頂驅控制器調諧I?k?c控制后，不同的系統工作參數下出現的粘滑振動和跳鉆現象均得到了有效的控制。因此，頂驅調諧I?k?c控制可以成功地消除輸入角速度和標稱鉆壓波動對鉆柱振動系統帶來的不利影響，比調諧k?c控制更能有效抑制鉆柱的粘滑振動和跳鉆現象。

參考文獻：

［1］FRANCA L F P. A bit-rock interaction model for rotary-percussive drilling［J］. International Journal of Rock Mechanics and Mining Sciences， 2011， 48（5）： 827-835.

［2］BERLIOZ A， DER HAGOPIAN J， DUFOUR R， et al. Dynamic behavior of a drill-string： experimental investigation of lateral instabilities［J］. Journal of Vibration and Acoustics， 1996， 118（3）： 292-298.

［3］GUPTA S K， WAHI P. Tuned dynamics stabilizes an idealized regenerative axial-torsional model of rotary drilling［J］. Journal of Sound and Vibration， 2018， 412： 457-473.

［4］GHASEMLOONIA A， RIDEOUT D G， BUTT S D. A review of drill string vibration modeling and suppression methods［J］. Journal of Petroleum Science and Engineering， 2015， 131： 150-164.

［5］JANSEN J D， VAN DEN STEEN L. Active damping of self-excited torsional vibrations in oil well drill strings［J］. Journal of Sound and Vibration， 1995， 179（4）： 647-668.

［6］YIGIT A S， CHRISTOFOROU A P. Stick-slip and bit-bounce interaction in oil-well drill strings［J］. Journal of Energy Resources Technology， 2006， 128（4）： 268-274.

［7］ZAMANIAN M， KHADEM S E， GHAZAVI M R. Stick-slip oscillations of drag bits by considering damping of drilling mud and active damping system［J］. Journal of Petroleum Science and Engineering， 2007， 59（3-4）： 289-299.

［8］KYLLINGSTAD A， NESSJ?EN P J. A new stick-slip prevention system［C］// Proceedings of SPE/IADC Drilling Conference and Exhibition. Amsterdam， The Netherlands， 2009： SPE-119660-MS.

［9］SARKER M M. Modeling， simulation and control of stick-slip and bit-bounce vibration in an oilwell drill string［D］. St. John’s： Memorial University of Newfoundland， 2012.

［10］鞏全成. 鉆柱粘滑振動非線性特征分析與魯棒控制研究［D］. 西安：西北工業大學，2015.

GONG Quancheng. Nonlinear characteristic analysis and robust control for drillstring stick-slip vibrations［D］. Xi’an： Northwestern Polytechnical University， 2015.

［11］AL SAIRAFI F A， AL AJMI K E， YIGIT A S， et al. Modeling and control of stick slip and bit bounce in oil well drill strings［C］// Proceedings of SPE/IADC Middle East Drilling Technology Conference and Exhibition. Abu Dhabi， UAE， 2016： SPE-178160-MS.

［12］韓善凱.鉆桿多向耦合振動及其控制研究［D］.天津：河北工業大學，2017.

HAN Shankai. Research on multi-direction coupling vibration of drill-strings and control［D］. Tianjin： Hebei University of Technology， 2017.

［13］張奇志，吳永強.抑制鉆柱黏滑振動和鉆頭反彈的建模與控制［J］.石油鉆采工藝， 2018， 40（5）： 553-558.

ZHANG Qizhi，WU Yongqiang. Modeling and control of restraining stick slip vibration of drill strings and bounce of drill bits［J］. Oil Drillinge & Production Technology， 2018， 40（5）： 553-558.

［14］付蒙，李江紅，吳亞鋒，等.基于狀態反饋和扭矩前饋鉆柱黏滑振動控制系統［J］.西北工業大學學報，2019，37（2）： 291-298.

FU Meng，LI Jianghong，WU Yafeng，et al. State feedback and torque feed forward combined control system for suppressing drill-strings stick-slip vibration［J］. Journal of Northwestern Polytechnical University， 2019， 37（2）： 291-298.

［15］付蒙，吳亞鋒，宋叔飆，等.抑制油氣井鉆柱黏滑振動控制器設計與應用［J］.振動與沖擊，2019，38（10）： 256-261.

FU Meng，WU Yafeng，SONG Shubiao，et al. Design and application of a control system to suppress the stick-slip vibration for oil-well drill strings［J］. Journal of Vibration and Shock， 2019， 38（10）： 256-261.

［16］ZHENG X， AGARWAL V， LIU X， et al. Nonlinear instabilities and control of drill-string stick-slip vibrations with consideration of state-dependent delay［J］. Journal of Sound and Vibration， 2020， 473： 115235.

［17］張奇志，許帥.分數階PID控制對鉆柱黏滑振動的抑制［J］.石油機械，2020， 48（3）： 44-50.

ZHANG Qizhi，XU Shuai. Suppression of stick-slip vibration of drill string by fractional-order PID control［J］. China Petroleum Machinery， 2020， 48（3）： 44-50.

［18］LIU X， ZHANG Z， ZHENG X， et al. Mitigation of stick-slip vibrations in drilling systems with tuned top boundary parameters［J］. Journal of Vibration and Acoustics， 2021， 143（5）： 051005.

［19］KYLLINGSTAD A. A comparison of stick-slip mitigation tools［C］//SPE/IADC Drilling Conference and Exhibition. The Hague， The Netherlands， 2017： SPE-184658-MS.

［20］HOSSEINZADEH A， BAKHTIARI-NEJAD F. A new dynamic model of coupled axial?torsional vibration of a drill string for investigation on the length increment effect on stick?slip instability［J］. Journal of Vibration and Acoustics， 2017， 139（6）： 061016.

Top drive control of axial-torsional coupled nonlinear vibration of drill string

DUAN Cong-cong1， LI Xin-ye1， ZHANG Li-juan2， ZHANG Hua-biao3， MA Chi-cheng1

（1.School of Mechanical Engineering， Hebei University of Technology， Tianjin 300401， China；2.School of Automobile and Transportation， Tianjin University of Technology and Education， Tianjin 300222， China；3.School of Mechanical Engineering， Tianjin University of Commerce， Tianjin 300134， China）

Abstract： In this paper， the effect of top drive control on stick-slip and bit-bounce was studied numerically based on a three-degree-of-freedom lumped parameter model considering coupling between axial and torsional vibrations of drill strings. The simulation results indicate that although the tuned k-c control can inhibit the stick-slip and bit-bounce the drill string vibration system to a certain extent， the suppression effect of stick-slip and bit-bounce in the drill string vibration system is not ideal when the input angular velocity is high and the nominal drilling pressure is low， or the input angular velocity is small and the nominal drilling pressure is large. The tuned I-k-c control can successfully eliminate the influence of input angular velocity and nominal drilling pressure changes on stick-slip and bit-bounce， so that no matter what the input angular velocity and nominal drilling pressure values are， the bit speed will remain stable around the given input angular velocity， reducing the fluctuation of WOB， TOB and axial displacement. Therefore， compared to top-drive tuned k-c control， tuned I-k-c control is more efficient in suppressing the stick-slip and bit-bounce of drill string vibration system.

Key words： nonlinear vibration； axial-torsional coupling of drill strings；top drive control；stick-slip；bit-bounce；lumped parameter model

作者簡介： 段聰聰（1996―），女，碩士研究生。E-mail： 1637402131@qq.com。

通訊作者： 李欣業（1966―），男，博士，教授。E-mail： xylihebut@163.com。