采用過濾白噪聲模型的地震動時域降維表達

摘要： 隨機地震動模擬一般有頻域和時域兩大類方法。本文基于單重過濾白噪聲時域模型，建議了平穩地震動過程和全非平穩地震動過程模擬的時域表達。本質上，時域表達可視為一系列標準正交隨機變量所調制的確定性函數的線性疊加，而正交隨機變量集則可定義為隨機正交函數形式來實現高效降維。為此，通過引入三類隨機正交函數，即非高斯型的Legendre正交多項式、Hartley正交基和高斯型的Hartley正交基，均可實現僅用一個基本隨機變量在時域模型上精細表達地震動加速度過程。平穩地震動過程的數值算例表明了本文方法的有效性，且優于Monte Carlo方法；全非平穩地震動的算例分析則表明了本文方法的工程適用性。

關鍵詞： 地震動過程； 時域表達； 過濾白噪聲； 降維模擬

中圖分類號： P315.9； TU311.3 文獻標志碼： A 文章編號： 1004-4523（2024）09-1493-08

DOI：10.16385/j.cnki.issn.1004-4523.2024.09.006

引 言

中國位于環太平洋地震帶與歐亞地震帶之間，是一個地震頻發的國家。強烈地震會造成工程結構的破壞，危害人類生命安全，造成重大經濟損失，因此，對工程結構進行合理的抗震分析具有重要意義［1］。目前，工程中常挑選若干實測強震記錄對結構進行抗震分析，這雖然便于工程應用，但由于實測記錄數量有限以及具體場地條件的限制，無法滿足工程抗震精細化分析的需求。因此，地震動過程的人工合成方法逐漸受到工程界和學術界的廣泛關注。一般而言，隨機地震動的模擬方法可分為時域方法和頻域方法兩大類。頻域方法主要適用于平穩過程的模擬，對于全非平穩地震動過程，往往需要引入時頻調制函數，由于時頻調制函數和平穩功率譜一般為慢變函數，因而難以很好地刻畫地震動局部的時頻全非平穩性，而且模擬時需要進行時頻域轉換，不可避免地引入誤差［2］。時域方法的模擬直接在時域上進行，且通過強度調制函數和時變濾波器，可實現時頻全非平穩，無需進行時頻域的轉換。為此，本文主要研究地震動模擬的時域方法。

地震動模擬的時域方法大致可分為調幅過濾白噪聲模型，時變ARMA模型等。時變ARMA模型本質上是一類機器學習模型，李英民等［3］對這類模型進行了較為系統的研究。由于時變ARMA模型的參數較多，且模型需要進行判階，因此本文僅研究調幅過濾白噪聲模型，該模型的發展有著悠久的歷史。Housner［4］率先提出采用隨機過程理論來模擬地震動加速度過程的思想。Bycroft［5］正式提出了平穩白噪聲地震動模型。然而，平穩白噪聲模型無法體現真實地震動的非平穩性，因此Shinozuka等［6］、Amin等［7］、Iyengar等［8］分別建議了強度調制函數來構造非平穩地震動模型。Yeh等［9］基于平穩濾波器構造高斯過濾白噪聲的地震動模型，并通過識別目標地震動的累積能量和向上穿零次數來確定其模型參數。隨后，Beck等［10］、Rezaeian等［11］、Vetter等［12］提出和發展了基于調幅過濾白噪聲的時域模型。該模型是一種半物理、半數據驅動模型，它以白噪聲過程作為原始隨機信號，經時變的濾波器過濾，最后通過調制函數來獲得全非平穩地震動。基于調幅過濾白噪聲的時域模型標志著地震動模擬的時域方法已趨于成熟，具有廣泛的應用前景。

在隨機地震動模擬的頻域方法中，無論是地震動過程的源譜表達［13］，還是地震動隨機場的離散表達［14?15］（譜表示與POD）以及連續表達［16］（波數譜），均可看作是一系列正交隨機變量與確定性函數之積的線性組合形式，這為引入隨機正交函數的約束來實現正交隨機變量集的高效降維提供了便利［17］。在本質上，隨機地震動模擬的時域方法也可看作類似形式，即一系列標準正交隨機變量所調制的確定性函數的線性疊加。因此，時域方法同樣也可以引入隨機正交函數來實現高效降維。而且，由于降維方法所生成的代表性樣本具有賦得概率，且構成一個完備的概率集，可與第三代結構設計理論相結合［18?20］，實現復雜工程結構的精細化動力響應分析與整體可靠度計算。

1 平穩地震動過程的單重過濾白噪聲模型

在地震工程中，平穩單重過濾白噪聲模型是指將地表土層視為單自由度的線性濾波器，而地震引起基巖運動的加速度過程假定為一個零均值的白噪聲過程，其雙邊功率譜密度為。于是，地表土層的運動方程［21］為：

（1）

式中 分別為地震地面相對于基巖的加速度、速度和位移響應；分別為地表土層的卓越圓頻率和阻尼比。

考慮到初始條件為零，根據Duhamel積分［21］，地震地面的相對位移響應為：

（2）

式中 “*”表示卷積符號；為相對位移的單位脈沖響應函數，即：

（3）

式中 。

根據卷積運算的微分性質，地震地面的相對速度響應為：

（4）

式中 為相對速度的脈沖響應函數，其表達式為：

（5）

于是，地震地面的絕對加速度可以表示為：

（6）

最后，將式（2）及式（4）代入到式（6）中，并利用式（3）和式（5），即可得到地震地面絕對加速度的單重過濾白噪聲表達式：

（7）

式中 表示絕對加速度的脈沖響應函數，即：

（8）

在式（2），（4）及式（7）中，平穩白噪聲過程應當滿足如下條件：

（9）

式中 E［］表示數學期望；為Dirac函數。

式（7）即為單重過濾白噪聲的時域模型，而對應的頻域模型就是地震工程中著名的Kanai?Tajimi譜［22］：

（10）

2 基于時域模型的平穩地震動過程模擬

為了便于模擬，對于平穩地震動加速度過程，需要將式（7）寫成分段積分的形式：

（11）

式中 經過k個時間步長后的時刻，為時間離散步長；表示地震動模擬持時T的時間離散項數；表示模擬時間t的時間離散項數。

在微小時間段內，假定為一常數，且略去式（11）中的最后一項。于是，式（11）可以近似寫成：

（12）

若令：

（13）

可以證明，（）是一組零均值的正交隨機變量。事實上有：

（14）

（15）

式中 為Kronecker符號。

進一步，將隨機變量進行標準化處理，即。于是，式（12）還可以簡寫成：

（16）

式中 為一組標準正交隨機變量集，即滿足如下的基本條件：

， （17）

3 基于時域模型的全非平穩地震動過程模擬

對于全非平穩地震動加速度過程，本文采用強度調制函數和時變的場地參數來描述時?頻全非平穩性。為此，根據式（7），全非平穩地震動加速度過程的時域模型為：

（18）

其中

（19）

在式（18）中，由于大括號內的部分是一個具有時變頻率成分的標準化過程（單位方差過程）。因此，強度調制函數就完全控制了過程的時間非平穩性，而脈沖響應函數（濾波器）及其時變參數則控制了過程的頻譜非平穩性。

一般地，強度調制函數可選用三段式模型［7］：

（20）

式中 參數，為地震動過程的標準差函數的最大值，變量c控制強度調制函數下降段的衰減速度。

對于脈沖響應函數的表達式（8），其參數采用如下的線性時變形式［23］：

（21）

式中 與分別為場地土卓越圓頻率和阻尼比的均值；a，b為場地土參數隨時間變化的速率。

同樣地，為了便于模擬，首先將式（18）中大括號內的部分寫成如式（11）所示的分段積分形式；然后，在微小時間段內，假定為一常數，且略去大括號內的最后一項，得到：

（22）

PIEMfolXGCQsqZhPkk5pd07v6ct3Zrn64KEN1kjh6bM=其中

（23）

最后，定義隨機變量，并進行標準化處理，即可得到式（22）的簡寫形式：

（24）

其中

（25）

值得指出的是，幾乎在以往所有的文獻里，都直接將隨機變量集當作是一組相互獨立的標準高斯隨機變量。這從Monte Carlo模擬的角度是十分方便的。但是，在本質上，隨機變量集應當是一組標準正交隨機變量，而且它們的概率分布也沒有給定，這恰為正交隨機變量集的降維提供了必要條件。此外，從式（16）及式（24）還可知，隨機過程的時域表達與Karhunen?Loève分解具有相同形式，他們都是將隨機過程表達為一系列確定性函數與正交隨機變量之積的線性組合形式。從這一意義來看，Karhunen?Loève分解可以視為是隨機過程時域表達的一種形式。

4 正交隨機變量集的降維表達

為了實現地震動過程時域表達的降維模擬，根據隨機正交函數的降維思想［13?17］，可以方便地構造以下三類正交隨機變量集的隨機正交函數形式［17］。

對于Legendre正交多項式，構造標準正交隨機變量集的隨機正交函數表達式為：

（26）

式中 基本隨機變量服從區間上的均勻分布；為Legendre正交多項式函數，其遞推公式為：

（27）

對于三角函數形式（Hartley正交基），可構造標準正交隨機變量集的隨機正交函數為：

（28）

式中 基本隨機變量服從區間上的均勻分布；常數通常取為。

上述兩類隨機正交函數形式所構造的（）一般都是非高斯型的標準正交隨機變量。為了構造高斯型的標準正交隨機變量集，根據式（28），并利用反變換法［17］，可得：

（29）

式中 為標準高斯分布函數的反函數；基本隨機變量服從區間上的均勻分布；常數通常取為。式（29）是基于Hartley正交基的高斯標準正交隨機變量集，簡稱為高斯型的Hartley正交基。

在式（26），（28）及式（29）中，i是j （）的重新排序，即i與存在著某種確定性的一一映射關系。這種一一映射關系通常可采用MATLAB工具箱中的rand（‘state’，0）和temp=randperm（N）函數來實現，即它們之間的一一映射關系為。這一映射關系恰為降維模擬方法的一個充分條件。

5 數值算例

5.1 平穩地震動過程的降維模擬分析

在應用式（16）和式（26），（28），（29）來模擬平穩地震動加速度過程時，需要首先確定時域模型的參數取值和基本隨機變量的代表性點集。

對于地震動單重過濾白噪聲模型，譜強度可按如下的公式計算［13，24］：

（30）

式中 為譜強度因子為1時的功率譜面積；為地震動峰值加速度的均值；為峰值因子。

在本算例中，以場地類別Ⅱ為例，地震動峰值加速度均值，峰值因子，場地土參數，；地震動模擬持時，時間步長。基本隨機變量的離散代表點公式如表1所示，其中代表點的數量，422，626三種情況。

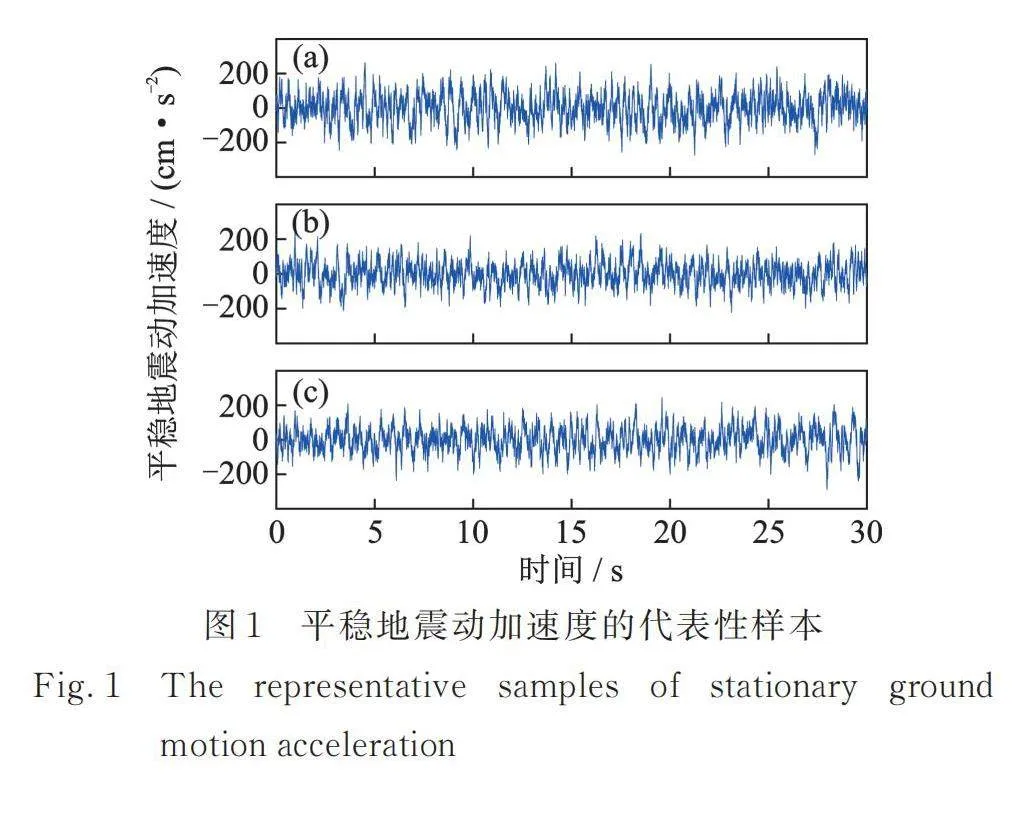
圖1為三類隨機正交函數降維方法生成的平穩地震動加速度代表性樣本，圖1中（a），（b），（c）分別采用了Legendre正交多項式、Hartley正交基以及高斯型的Hartley正交基。可見，代表性樣本均具有良好的平穩特性。

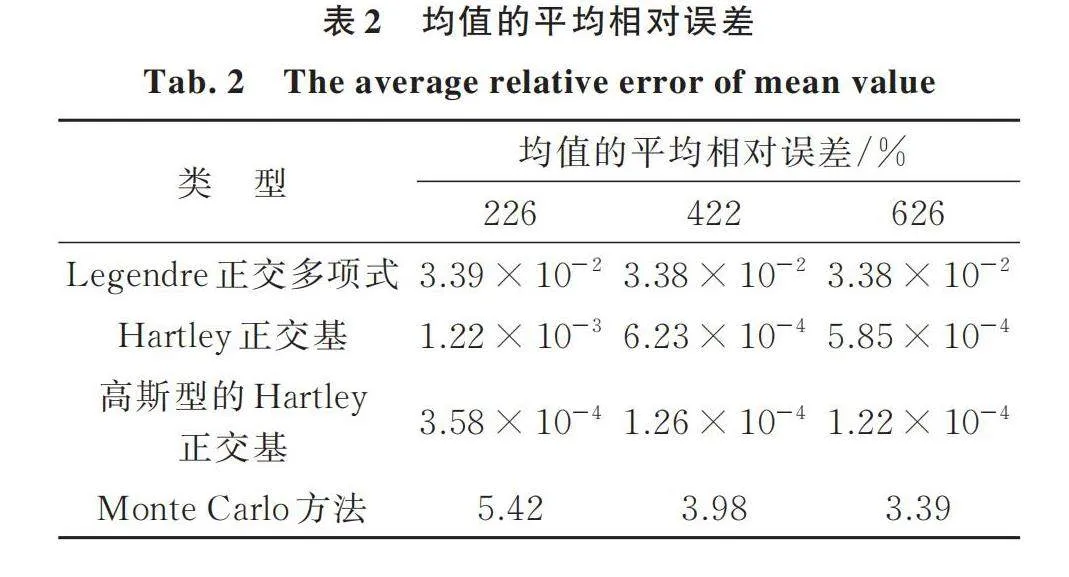
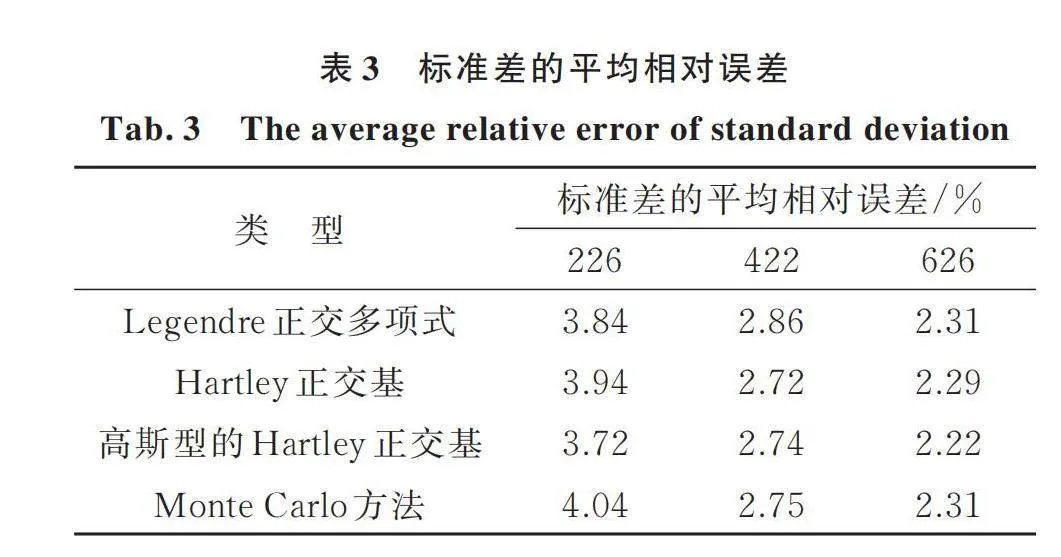
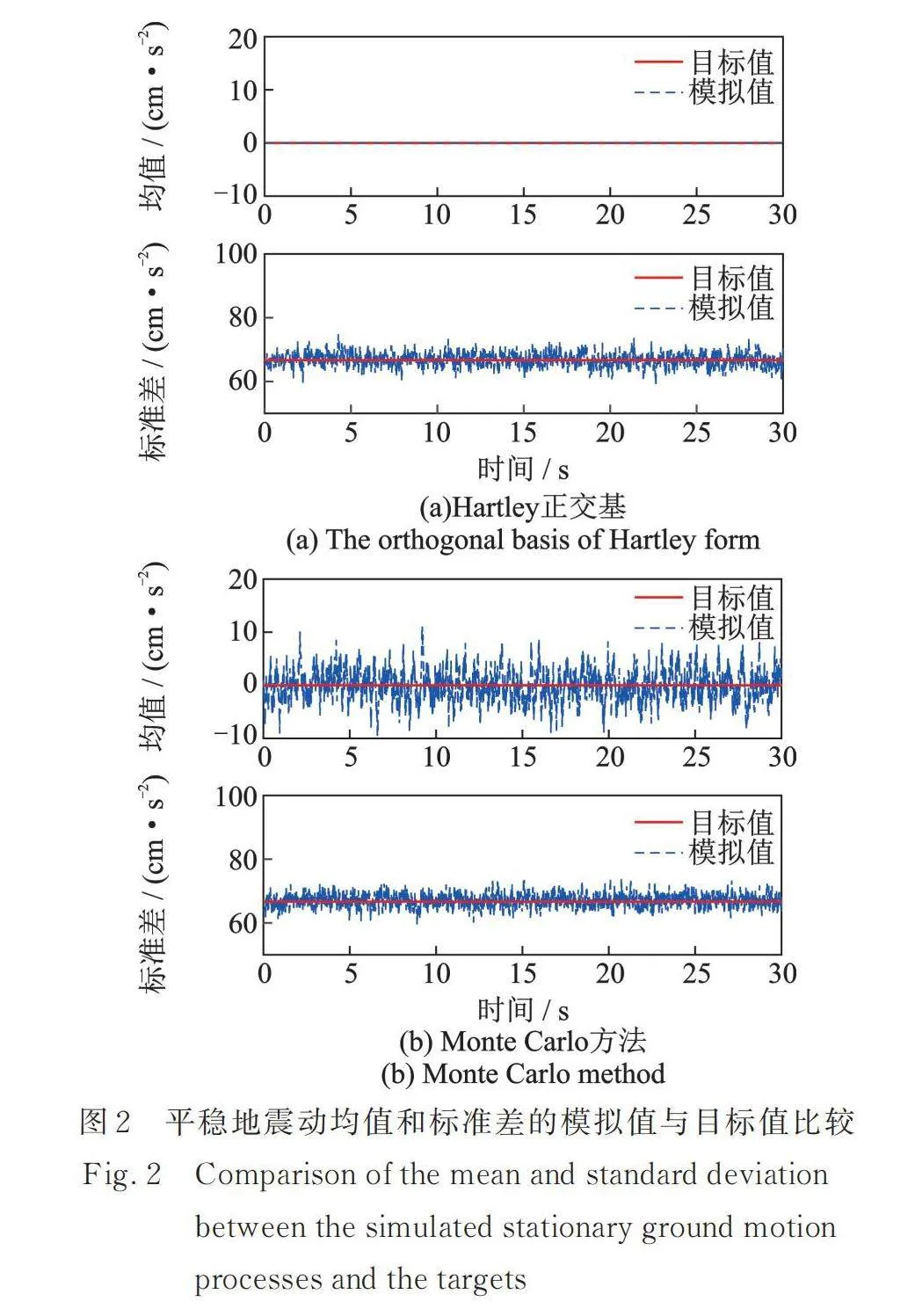
為了進一步說明降維方法的有效性，現將本文方法與Monte Carlo方法進行對比分析。圖2為平穩地震動加速度過程的均值和標準差的模擬值與目標值比較，其中圖2（a）采用了Hartley正交基（非高斯型）的降維方法，圖2（b）采用了相互獨立的標準高斯隨機變量的Monte Carlo方法。直觀地看，本文降維方法模擬平穩地震動加速度過程的均值明顯優于Monte Carlo方法；對標準差而言，兩種方法的差異性不大。表2和表3分別給出了均值和標準差的平均相對誤差，由表可見，對于三類隨機正交函數的降維方法，所生成平穩地震動加速度過程的代表性樣本集合的誤差均比較接近，說明降維方法具有普適性。同時，高斯型的Hartley正交基模擬精度最高，Hartley正交基次之，Legendre正交多項式相對較差。因此，若對模擬精度要求較高時，可選用高斯型的Hartley正交基。此外，對于每一類隨機正交函數，隨著代表性樣本數量的增加，均值和標準差的平均相對誤差都是逐漸減小的，這表明降維方法具有良好的魯棒性。

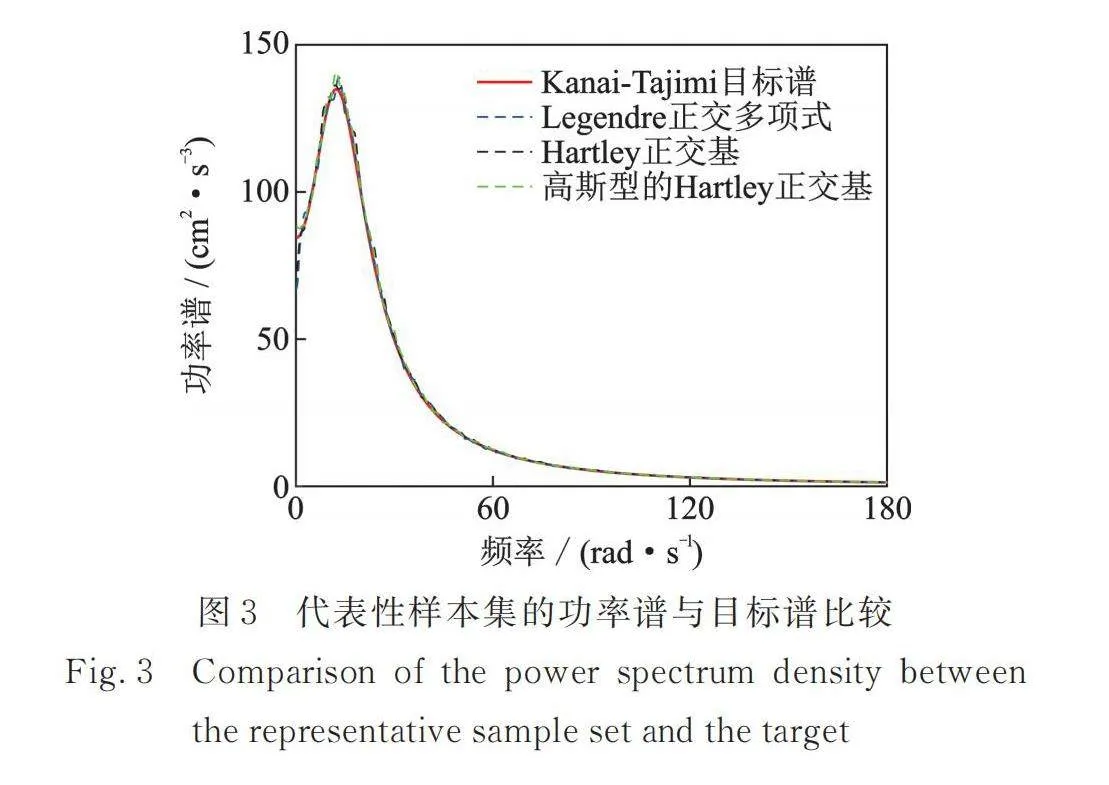
利用三類隨機正交函數的降維方法，生成平穩地震動加速度過程的代表性樣本集，圖3為422條代表性樣本集的單邊功率譜與單邊目標譜的比較。可見，代表性樣本集的功率譜與目標譜擬合良好。

表4給出了代表性樣本集的功率譜平均相對誤差。在總體上，三類隨機正交函數的降維方法要比Monte Carlo方法的平均相對誤差略小。而且隨著代表性樣本數量的增加，功率譜平均相對誤差逐漸減小。這進一步說明了隨機正交函數降維方法的有效性和優越性。

5.2 全非平穩地震動過程的降維模擬分析

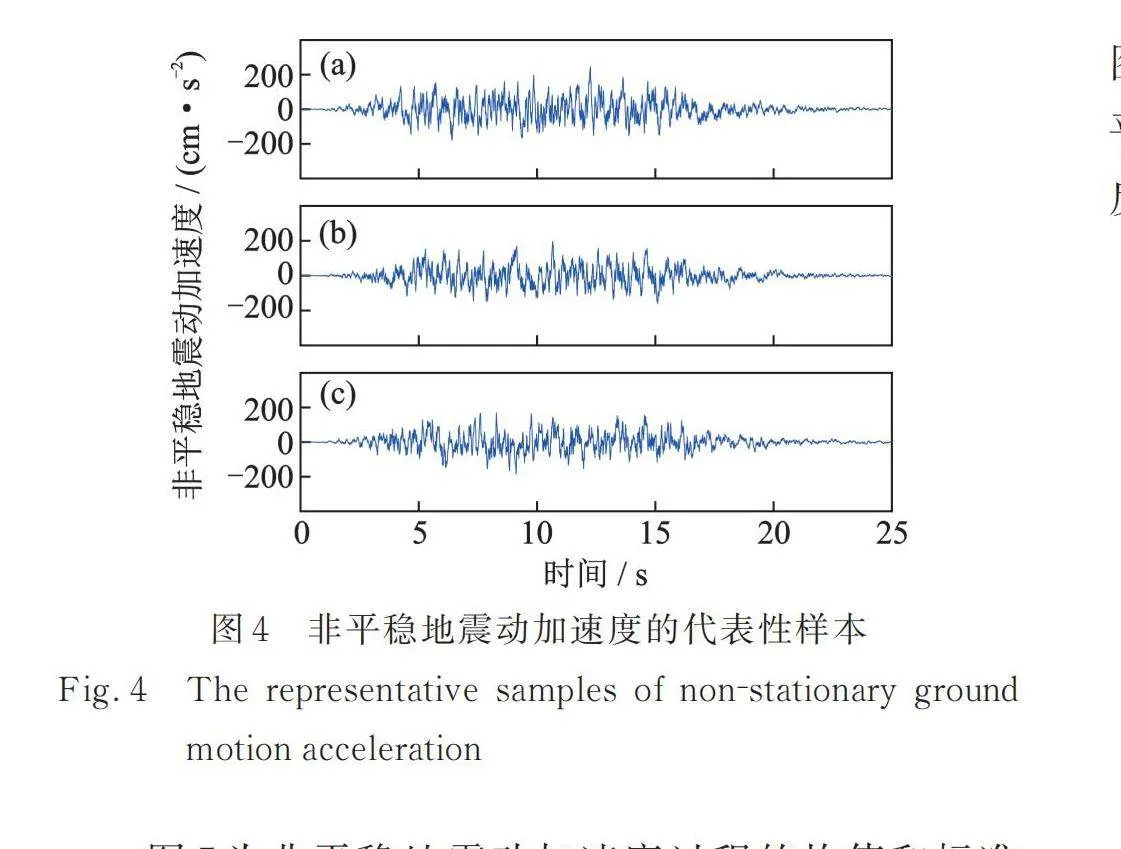
在全非平穩地震動過程的降維模擬中，以場地類別Ⅱ和設計地震分組第二組為例。其中，地震動峰值加速度均值，峰值因子；場地土參數，，，；地震動模擬持時，時間步長；強度調制函數參數，，，。基本隨機變量的離散代表點公式如表1所示，其中代表點的數量。圖4為三類隨機正交函數降維方法所生成的全非平穩地震動加速度代表性樣本，圖4中（a），（b），（c）分別采用了Legendre正交多項式、Hartley正交基以及高斯型的Hartley正交基。顯然，代表性樣本均具有良好的強度和頻率非平穩特性。

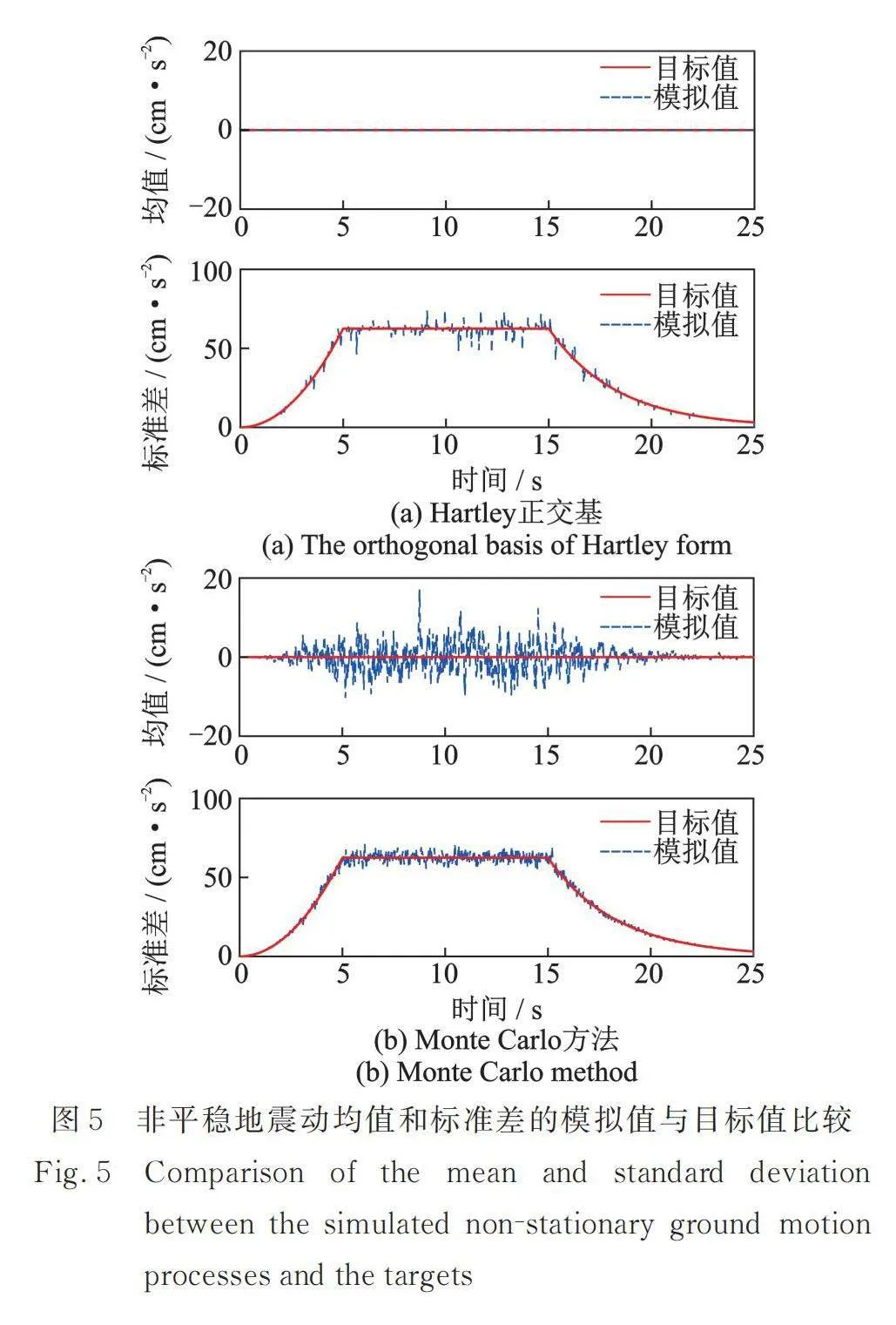
圖5為非平穩地震動加速度過程的均值和標準差的模擬值與目標值比較，其中圖5（a）采用了Hartley正交基（非高斯型）的降維方法，圖5（b）采用了相互獨立的標準高斯隨機變量的Monte Carlo方法。可見，本文建議的降維方法模擬非平穩地震動加速度過程的均值和標準差都優于Monte Carlo方法。

為進一步從地震反應譜來闡明本文降維方法的工程適用性，圖6給出了三類隨機正交函數降維方法所生成的非平穩地震動加速度反應譜與規范反應譜的比較，其中規范反應譜對應于《建筑抗震設計規范》［25］中場地類別Ⅱ和設計地震分組第二組。從圖6可知，三類隨機正交函數降維方法所生成的非平穩地震動加速度反應譜幾乎重合，且它們與規范反應譜擬合良好。

6 結論與展望

基于時域的單重過濾白噪聲模型，給出了平穩地震動加速度過程模擬的時域表達，進一步通過引入強度調制函數以及場地土的時變參數模型，建立了全非平穩地震動加速度過程模擬的時域表達。在此基礎上，通過引入標準正交隨機變量集的三類隨機正交函數形式，實現了地震動加速度過程的降維模擬。其結論與展望如下：

（1） 在平穩地震動過程和非平穩地震動過程模擬的時域表達中，都是通過一系列標準正交隨機變量來實現的。而傳統的Monte Carlo方法則是利用一系列相互獨立的標準高斯隨機變量。然而，標準正交隨機變量集可以通過基本隨機變量的正交函數（即隨機正交函數）來實現降維。事實上，隨機過程模擬的時域表達與頻域表達均可通過隨機正交函數來實現其降維模擬。

（2） 對于平穩地震動加速度過程，其時域表達中包含了時間步長，因此需要足夠小的時間步長才能獲得理想的模擬效果。為此，可以像全非平穩地震動加速度過程模擬的時域表達，采用標準化過程來消除時間步長的影響，從而提高模擬效率。

（3） 隨機正交函數降維方法的最大優點在于實現了僅用一個基本隨機變量即可精細地表達地震動加速度過程，從而僅需數百條代表性樣本就能在全概率上反映地震動過程的概率信息。這為結合概率密度演化理論進行復雜工程結構的精細化抗震分析提供了重要基礎。

（4） 本文僅給出了單重過濾白噪聲模型，事實上，還可以推導出二重過濾白噪聲等模型。而且，對于非平穩地震動加速度過程的時域表達，也可以給出不同的強度調制函數和場地土的時變參數模型。這將在后續研究中進一步完善。

參考文獻：

［1］楊慶山， 田玉基. 地震地面運動及其人工合成［M］. 北京： 科學出版社， 2014.

Yang Qingshan， Tian Yuji. Earthquake Ground Motions & Artificial Generation［M］. Beijing： Science Press， 2014.

［2］歐進萍， 王光遠. 結構隨機振動［M］. 北京： 高等教育出版社， 1998.

Ou Jinping， Wang Guangyuan. Random Vibration of Structure［M］. Beijing： Higher Education Press， 1998.

［3］李英民， 劉立平. 工程結構的設計地震動［M］. 北京： 科學出版社， 2011.

［4］Housner G W. Characteristics of strong-motion of earthquakes［J］. Bulletin of the Seismological Society of America， 1947， 37（1）： 19-31.

［5］Bycroft G N. White noise representation of earthquakes ［J］. Journal of the Engineering Mechanics Division， 1960， 86（2）： 1-16.

［6］Shinozuka M， Deodatis G. Stochastic process models for earthquake ground motion［J］. Probabilistic Engineering Mechanics， 1988， 3（3）： 114-123.

［7］Amin M， Ang A. Non-stationary stochastic model of earthquake motion［J］. Journal of the Engineering Mechanics Division， 1968， 94（2）： 559-584.

［8］Iyengar R N， Iyengar K T S R. A nonstationary random process model for earthquake accelerograms［J］. Bulletin of the Seismological Society of America， 1969， 59（3）： 1163-1188.

［9］Yeh C H， Wen Y K. Modeling of nonstationary ground motion and analysis of inelastic structural response［J］. Structural Safety， 1990， 8（1-4）： 281-298.

［10］Beck J L， Papadimitriou C. Moving resonance in nonlinear response to fully nonstationary stochastic ground motion［J］. Probabilistic Engineering Mechanics， 1993， 8（3-4）： 157-167.

［11］Rezaeian S， Der Kiureghian A. A stochastic ground motion model with separable temporal and spectral nonstationarities［J］. Earthquake Engineering and Structural Dynamics， 2008， 37（13）： 1565-1584.

［12］Vetter C R， Taflanidis A A， Mavroeidis G P. Tuning of stochastic ground motion models for compatibility with ground motion prediction equations［J］. Earthquake Engineering and Structural Dynamics， 2016， 45（6）： 893-912.

［13］Liu Z J， Liu W， Peng Y B. Random function based spectral representation of stationary and non-stationary stochastic processes［J］. Probabilistic Engineering Mechanics， 2016， 45： 115-126.

［14］Liu Z X， Liu Z J， Ruan X X， et al. Spectral representation-based dimension reduction for simulating multivariate non-stationary ground motions［J］. Soil Dynamics and Earthquake Engineering， 2018， 114： 313-325.

［15］劉章軍， 劉子心， 阮鑫鑫， 等. 地震動隨機場的POD降維表達［J］. 中國科學： 技術科學， 2019， 49（5）： 589-601.

Liu Zhangjun， Liu Zixin， Ruan Xinxin， et al. POD-based dimension reduction representation of stochastic ground motion fields［J］. Scientia Sinica （Technologica）， 2019， 49（5）： 589-601.

［16］Ruan X X， Liu Z J， Liu Z X， et al. Dimension-reduction representation of stochastic ground motion fields based on wavenumber-frequency spectrum for engineering purposes［J］. Soil Dynamics and Earthquake Engineering， 2021， 143： 106604.

［17］Liu Z J， Liu Z X， Peng Y B. Dimension reduction of Karhunen-Loeve expansion for simulation of stochastic processes［J］. Journal of Sound and Vibration， 2017， 408： 168-189.

［18］Li J， Chen J B. Stochastic Dynamics of Structures ［M］. Singapore： John Wiley & Sons， 2009.

［19］Li J， Chen J B. The principle of preservation of probability and the generalized density evolution equation［J］. Structural Safety， 2008， 30（1）： 65-77.

［20］李杰. 工程結構可靠性分析原理［M］. 北京： 科學出版社， 2021.

Li Jie. Fundamental of Structural Reliability Analysis ［M］. Beijing： Science Press， 2021.

［21］劉章軍，陳建兵，彭勇波. 結構動力學［M］. 北京：中國建筑工業出版社， 2022.

［22］Kanai K. An empirical formula for the spectrum of strong earthquake motions［J］. Bulletin of Earthquake Research Institute， 1961， 39（1）： 85-95.

［23］劉章軍， 劉子心. 基于規范反應譜的全非平穩地震動過程模擬［J］. 振動工程學報， 2017， 30（3）： 457-465.

Liu Zhangjun， Liu Zixin. Simulation of fully non-stationary ground motion based on seismic design response spectrum［J］. Journal of Vibration Engineering， 2017， 30（3）： 457-465.

［24］Seya H， Talbott M E， Hwang H H M. Probabilistic seismic analysis of a steel frame structure［J］. Probabilistic Engineering Mechanics， 1993， 8（2）： 127-136.

［25］中華人民共和國住房和城鄉建設部，中華人民共和國國家質量監督檢驗檢疫總局. 建筑抗震設計規范：GB 50011—2010 ［S］. 北京： 中國建筑工業出版社， 2010.

Ministry of Housing and Urban-Rural Development of the People’s Republic of China， General Administration of Quality Supervision， Inspection and Quarantine of the People’s Republic of China. Code for seismic design of buildings： GB 50011—2010［S］. Beijing： China Architecture & Building Press， 2010.

Dimension-reduction representation of seismic ground motion using filtered white noise model in time domain

LIU Zhang-jun1， FAN Ying-fei1， Jiang Yun-mu1， Ruan Xin-xin1， Liu Zi-xin2

（1.School of Civil Engineering and Architecture， Wuhan Institute of Technology， Wuhan 430074， China；2.Key Laboratory of Building Collapse Mechanism and Disaster Prevention，Institute of Disaster Prevention，China Earthquake Administration， Sanhe 065201， China）

Abstract： There are two kinds of stochastic seismic ground motion simulation methods： frequency-domain methods and time-domain methods. Based on the time-domain model of single filtered white noise， this paper proposes the time-domain representation for simulating stationary and non-stationary seismic ground motion processes. In essence， the time-domain representation can be regarded as linear superposition of deterministic functions modulated by a series of standard orthogonal random variables， and the set of orthogonal random variables is defined as the form of random orthogonal functions to achieve efficient dimension-reduction. Therefore， by introducing three kinds of random orthogonal functions， i.e.， Legendre orthogonal polynomial of non-Gaussian type， Hartley orthogonal basis and Hartley orthogonal elementary of Gaussian type， the acceleration process of seismic ground motion can be accurately represented in the time-domain model with only one elementary random variable. Numerical examples of seismic stationary ground motion process show the effectiveness of the proposed method， which is superior to the Monte Carlo method. The analysis of fully nonstationary seismic ground motion shows the engineering applicability of the proposed method.

Key words： ground motion process；time domain representation；filtered white noise model；dimension-reduction simulation

作者簡介： 劉章軍（1973―），男，博士，教授，博士生導師。E-mail： liuzhangjun73@aliyun.com。

通訊作者： 劉子心（1988—），女，博士，副教授，碩士生導師。E-mail： liuzixin@cidp.edu.cn。