遵循認知規律，注重過程體驗，提升數學素養

摘要：文章記述了“矩形的性質”一課的教學預設及教學過程.教師在設計教學時，通過讓學生類比平行四邊形性質的探究路徑展開探索，在過程體驗中感受數學思想，積累活動經驗，提升數學素養.通過教學實踐，提出理解學生、理解教材、理解教學可以讓教學更具適應性、針對性和有效性.

關鍵詞：認知規律；數學素養；矩形的性質

教學規律是通過大量教學實踐探索得出的，是隨著教學實踐的發展變化而發展的.新課改風向標下，數學課堂發生了翻天覆地的變化，不管是情境的創設還是活動的設計，都指向了對教學規律的研究.教師唯有從理解學生、理解教材、理解教學的角度設計教學，才能提高教學的針對性、有效性和適應性[1].據此，筆者結合“矩形的性質”一課的教學，談談如何遵循認知規律優化教學設計，提高學生的數學素養.

1 課前思考

基于生長數學的視角，可以發現“矩形”一課有著明顯的生成路徑，原因在于學習該內容時學生已然具備了研究平行四邊形的探究經驗，類比平行四邊形的探究路徑來探究矩形不僅利于新知的建構，而且對后續菱形、正方形性質的學習可以起到促進作用.進一步分析教材可知，本節課是矩形第一課時，且探究的是矩形概念及相關性質，因此不能僅僅停留在知識的傳輸層面，還需注重過程體驗，引領學生經歷圖形基本性質的探究過程，以發展基本推理能力.

2 教學過程

教學目標：（1）知識與技能.掌握矩形的基本性質，包括對角線相等、對角線互相平分、內角為直角等；（2）過程與方法.通過類比探究，掌握矩形性質的推導過程，培養有效推理能力；（3）情感態度與價值觀.激發對幾何的學習興趣，增強邏輯思維能力.

環節1情境導入，引發興趣

師：同學們，請你們仔細觀察老師手中的書本，它有什么特別的地方嗎？

生1：它有四條邊，而且它的角都是直角.

師：很好，觀察得很仔細.我們可以更精確地描述它的特征，它的幾個角是直角呢？

生2：它的四個角都是直角.

師：非常好！那么，今天我們就來研究一下矩形這種常見的幾何圖形，看看它到底有哪些性質.

環節2類比探究，有所感悟

師：（展示不同的四邊形：平行四邊形、菱形、矩形、正方形）請同學們觀察這些圖形，你們發現它們有哪些共同點和不同點？

生1：它們都有四條邊.

生2：它們的對邊都平行.

生3：正方形和矩形的四個角都是直角，其他圖形不是.

…………

師：很好，觀察得很仔細.讓我們用數學的語言來總結一下矩形和正方形的區別.①邊長：矩形對邊相等，即相對的兩條邊長度相等，但四條邊的長度不一定相等，正方形四條邊長度都相等；②對角線：矩形的對角線相等且互相平分，正方形的對角線相等且互相平分，并且對角線互相垂直；③內角：矩形的四個內角都是直角（90°），正方形的四個內角也是直角（90°）；④特殊性質：矩形沒有所有邊相等的限制，只要求對邊相等和四個直角.正方形既具備矩形的所有性質（對邊相等且平行、四個直角），又具備所有邊相等和對角線互相垂直的特性.正方形是特殊的矩形，也是特殊的菱形.

環節3有效推理，獲取認識

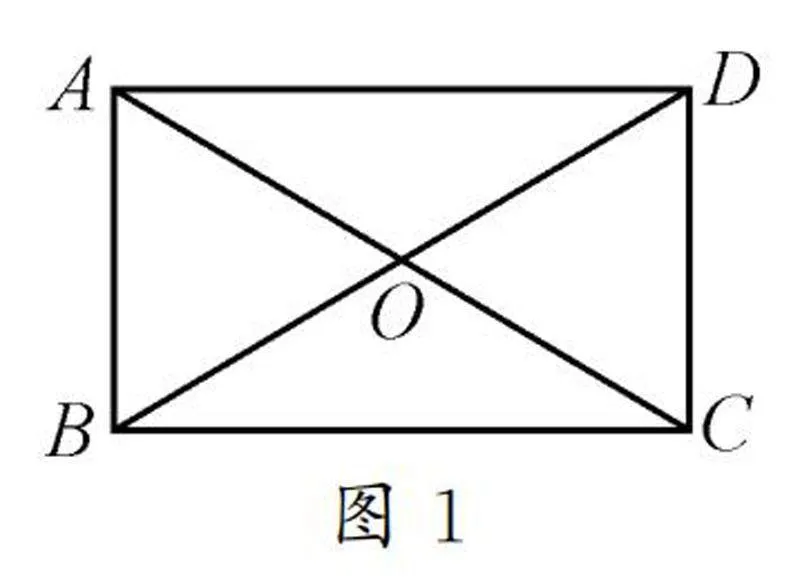
師：請同學們觀察圖1，除了前面總結的矩形性質，我們還可以得到哪些信息呢？

生1：可以發現OA=OB=OC=OD.

生2：對角線將該矩形分為四個面積相等的等腰三角形.

師：非常好！還有其他發現嗎？

生3：發現這個矩形中有四個特殊三角形是四個全等的直角三角形.

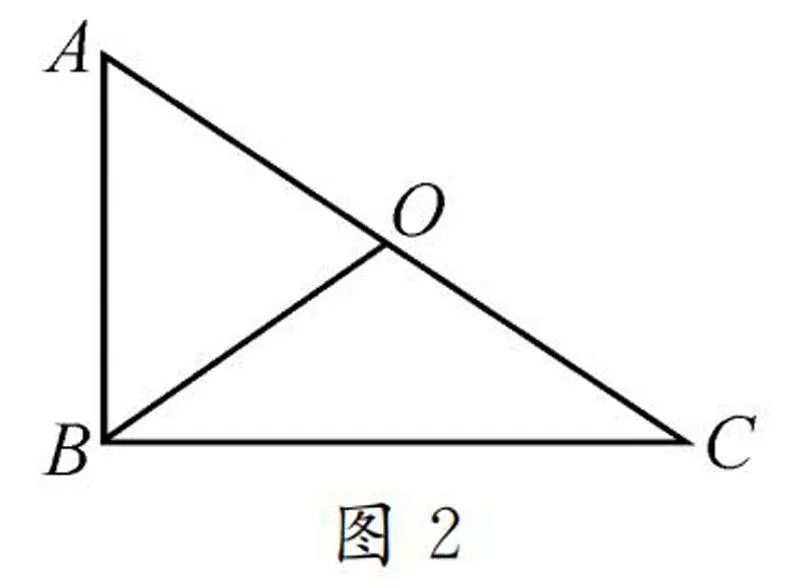
師：很好.觀察圖2所示的直角三角形，你們有沒有什么新發現？

生4：OA=OB=OC，即直角三角形中，斜邊中線等于斜邊的一半.

師：非常好！你們通過觀察和推理，不僅發現了矩形的一些基本性質，還推導出了直角三角形的一個重要性質.這說明你們已經很好地掌握了這些幾何知識，并且能夠靈活運用.

環節4課堂小結，深化認識

師：請同學們總結一下，矩形有哪些主要的性質？

生（齊）：矩形有四個直角.

師：很好，這是矩形的一個重要性質.還有其他的性質嗎？

生1：矩形的對角線相等且互相平分.

師：非常好，總結得很全面.那么，同學們知道矩形在我們生活中有哪些應用嗎？

生2：書本的封面和每一頁都是矩形.

師（繼續引導）：非常正確！書本是一個很好的例子.為什么書本會設計成矩形的形狀呢？

生3（嘗試回答）：可能是因為矩形有四個直角，便于印刷和裝訂，而且每一頁內容都可以對齊.

師：說得很好.除了這些，矩形的設計還有什么好處呢？

生4（思考后回答）：矩形的書本還容易疊放和攜帶，這樣可以節省空間.

師：完全正確.矩形的設計確實具有實用性和美學價值.它在我們的生活中無處不在，不僅方便了我們的生活，還為我們帶來了美的享受.希望同學們能夠在學習和生活中多加留意，發現更多關于矩形的應用.

環節5深化認識，拓展應用

師：通過本節課的學習，我們已經了解了矩形的許多性質.那么，老師想給大家一個拓展任務，你們在生活中能發現哪些矩形的應用實例呢？

生1：家里裝修時，我發現師傅們都會用矩形瓷磚來鋪地，這樣可以確保地面平整，容易對齊.

師：這個例子也很好.矩形瓷磚確實利用了矩形的性質，確保地面鋪設得美觀和穩固.那么，矩形的哪個性質在這里特別重要呢？

生2：我覺得可能是矩形對角線相等和互相平分的性質，這樣可以確保每塊瓷磚都能對齊.

師：非常棒！這個性質在實際應用中確實非常重要.比如，在制作和檢測桌子、書柜等家具時，這個性質就尤為關鍵.誰能詳細解釋一下呢？

生3：通過測量對角線長度來確保每個角度都是90°，從而保證家具的平整和穩定.

師：很好.如果對角線長度相等且中點重合，就能確認家具的形狀是標準的矩形，這樣制作出來的家具不僅美觀，還能保證其穩固性和功能性.通過這節課的學習，希望大家不僅掌握了矩形的性質，還能在生活中應用這些知識.

3 教學反思

3.1 理解學生，讓教學更具適應性

培養學生的數學核心素養，提升學生分析和解決問題的能力，單純地依靠解題是難以實現的，而需讓學生參與數學探究，經歷知識生成過程，才能積累一定的活動經驗[2].為此，本節課中教師能遵循學生認知規律，通過問題引領探究，幫助學生初步感受矩形性質的特殊之處在于“對平行四邊形的一個內角條件的強化”，體驗研究路徑的類似，從而輕車熟路地展開對矩形性質的探究.就這樣，經歷知識生成的過程，在類比和對比的過程中深化認識，實現對數學知識和方法的深刻理解，有效發展數學素養.

3.2 理解教材，讓教學更具針對性

四邊形概念、要素、性質等的教學是類比三角形展開的，通過回顧三角形的探究過程，逐步形成了幾何圖形研究的一般性思路，實現了知識和方法的共同生長，同時明確了幾何圖形的研究路徑，即“定義—性質—判定—應用”，如需深入，則是探討圖形的特例.因此，在設計本節課的教學活動時，筆者充分尊重教材，并挖掘教材內涵進行提問，讓所有問題圍繞類比和對比展開，讓學生體會幾何圖形的一般研究范式，從而有效滲透類比思想，促進知識體系的建構.

3.3 理解教學，讓教學更具有效性

提高基于具體學情和教學內容的探究活動的有效性，教學的著力點不僅在于知識的獲取，更在于學習過程中的體驗和感悟、數學思想的體驗及活動經驗的積累[3].本課中，教師注重引導學生觀察平行四邊形動態變化的過程，讓學生切實體驗變化的性質、不變的性質及變化的規律，從而在變與不變中豐富學生的世界觀.教是為了不教，在課堂中注重引導學生經歷和體驗，讓學生自主發現和建構，不僅有助于知識網絡的構建，還有利于后續菱形等的學習，更重要的是幫助學生掌握研究的方法和思路.

總之，培養學生的數學素養并非一蹴而就的，需要滲透在每一節課中，并一以貫之地把握課堂教學中各個環節的設計，做到遵循學生認知規律，關注學生已有知識水平、數學思維和已有經驗，真正意義上注重過程體驗，才能提高學生探究的參與度，讓學生真正進入深度學習，有效提高數學核心素養.

參考文獻：

[1]徐淮源.基于教材理解下的高中數學概念教學設計——以“三角函數的周期性”為例[J].教育研究與評論（中學教育教學），2010（2）：73-78.

[2]陳明鐘.實施過程性教學模式 構建初中數學高效課堂[J].中學數學，2016（8）：68-70.

[3]夏炳文.強化“三個理解” 打造活力課堂——以一節試卷講評課為例[J].中國數學教育，2016（10）：42-44，56.