感悟數學之

摘要：眾所周知，培養學生數學學習興趣是學好數學的關鍵.在初中數學教學中，教師要摒棄單一的知識講授，有意識地展示、傳播數學之美，并帶領學生一起探索、發現數學之美，從而讓學生充分體驗數學學習的樂趣，激發學生潛能，獲得成功的喜悅和美的享受，進而讓學生愛上數學.

關鍵詞：興趣；數學之美；樂趣

通過數學學習，不僅要讓學生掌握數學知識，提高數學成績，還要培養學生數學學習的興趣，提高學生學習數學的積極性和主動性.在日常教學中，教師應有意識地傳播數學之美，并創造機會讓學生體驗數學之美，從而激發學生對數學的學習興趣.而數學之美散落于教材的各個角落，教師要去挖掘，并創造機會讓學生去欣賞、體驗和感悟，以此充分展示數學的魅力.

勾股定理將數與形完美地融合在一起，其中蘊含著豐富的美學資源.教學中，教師應引導學生多視角思考與觀察，主動探尋蘊含其中的美妙的數量關系，充分感受美、發現美、驗證美，構建高效生本課堂.

1 深入挖掘，凸顯本質

在初中數學教學中，若想讓學生真正地理解知識，僅將知識講授給學生并不夠，還要關注學生對數學本質的認識，重視引導學生運用所學知識分析問題和解決問題，讓學生在學習數學的過程中找到樂趣，提高學生的數學素養和創新能力.在解題過程中，教師要引導學生多思考幾個“為什么”，在刨根問底中弄清實質，提高學生的數學能力，讓學生感受數學之美.

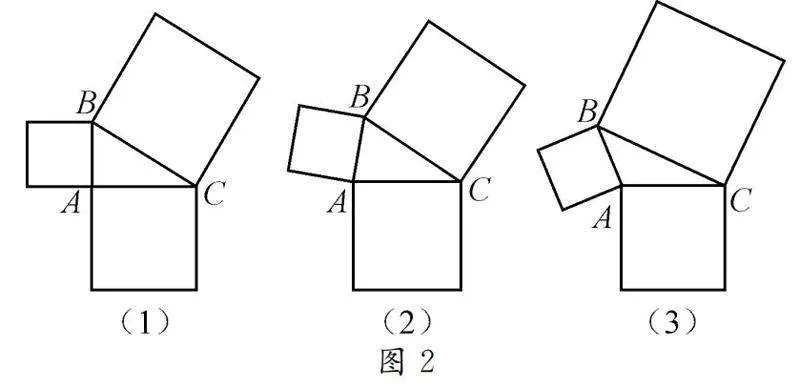
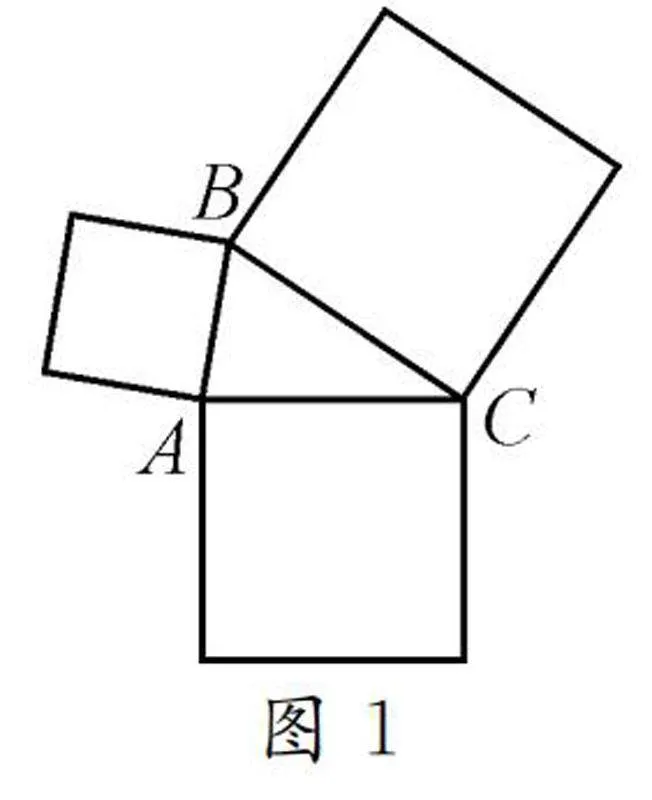
例如圖1，已知△ABC是銳角三角形，分別以AB，BC，AC為一邊作圖1所示的正方形，假設BC邊最長，則以BC邊為邊長的大正方形與另外兩個正方形存在怎樣的數量關系？如果△ABC是鈍角三角形，其中BC邊最長，你又能得到怎樣的數量關系？

師生活動：問題給出后，教師讓學生獨立思考，探尋蘊含其中的一般規律.從學生反饋來看，很多學生結合已有知識和經驗，利用割補法計算正方形的面積，發現蘊含其中的美妙的數量關系.在此基礎上，教師繼續追問“是什么原因導致這種現象呢？”在問題的驅動下，學生繼續思考，逐漸逼近問題的本質.

探究過程如下：

如圖2（1），結合已有知識經驗可知，當∠BAC=90°時，AB²+AC²=BC²；如圖2（2），保持AC與AB的長度不變，并保證BC邊依然為最長邊的前提下，調整∠BAC的大小，使得∠BAC<90°，顯然此時BC變短了，顯然大正方形的面積變小了，而兩個小正面形的面積和保持不變，所以AB²+AC²>BC²；同理，如圖2（3），在確保BC邊為最長邊，AC與AB的長度不變的前提下，繼續調整∠BAC的大小，使得∠BAC>90°，顯然BC變長了，所以大正方形的面積變大了，而兩個小正面形的面積和保持不變，所以AB²+AC²<BC².這樣以直角三角形為基礎，通過調整兩個小正方形的夾角大小，引領學生體會面積之間的數量關系，揭示“角變化引起邊變化”的實質.

設計意圖：在研究勾股定理時，運用“勾股樹”證明勾股定理，即以直角三角形的各邊為邊長向外作正方形，通過割補得到兩個小正方形的面積之和等于大正方形面積，從而得到勾股定理.該題將直角三角形轉化為銳角三角形和鈍角三角形，通過由特殊到一般的轉化，點燃學生的探究欲.同時通過由一般到特殊的探究，有利于加深學生對相關知識、方法的理解，摒棄單一的模仿和套用，讓學生通過探究感悟數學知識之間的區別與聯系，培養思維的深刻性.另外，為了探究產生這一現象的本質原因，教師進行適度引導，讓學生在變與不變中認清問題的本質，以此提高學生發現、分析和解決問題的能力，彰顯數學探究之美，提高學生數學思維品質.

2 借助問題，引領發現

在傳統數學教學中，師生所關注的往往是解題方法和解題技巧，學生眼中的數學往往是枯燥的、乏味的，不利于學生學習興趣的培養.基于此，在實際教學中，教師要預留時間讓學生去探索、去交流，引導學生發現數學之美.

例如，通過對例1的多層次探究，學生得到并驗證了一般結論.在此基礎上，教師啟發學生繼續思考這樣幾個問題：

（1）若其中直角變大和變小的度數一樣，那么是不是減少的面積恰好為變大的面積呢？

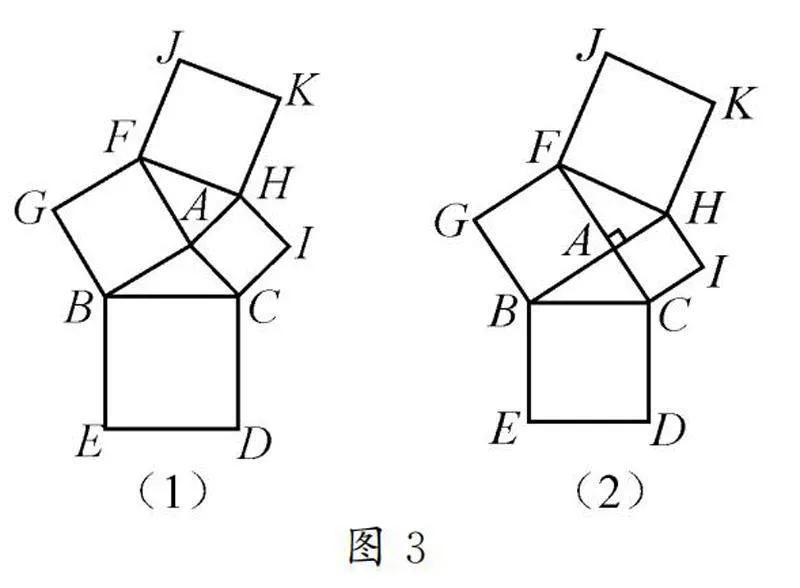
（2）假如圖2（2）和圖2（3）中減少和增加的度數一樣，先將其合并為圖3（1），與圖3（2）相比較，是不是圖3（1）中正方形FHKJ與正方形BCDE的面積之和等于圖3（2）中正方形FHKJ與正面形BCDE的面積之和呢？

師生活動：教師讓學生以小組為單位，通過合作學習的方式共同探尋問題的答案.圖3（2）中，根據勾股定理易得S+S=2（S+S），于是學生可以將該問題轉化為：圖3（1）中，S+S=2（S+S）是否成立？為了讓學生直觀體驗其中的一般規律，教師利用幾何畫板進行動態演示，學生通過直觀觀察發現以上結論成立.

設計意圖：教學中，教師通過創設問題繼續引導學生挖掘蘊含其中的一般規律，引導學生用數學的眼光看世界，充分體會數學的和諧美、對稱美、簡約美，激發學生學習數學的積極性.以上結論是通過猜想、對比、觀察得到的，并未進一步驗證，所以并不能作為結論，教師還應提供時間讓學生利用已學數學知識進一步驗證，以此讓學生體會數學的嚴謹美.

3 突破疑難，提升能力

嚴謹性是數學的獨特之美，任何數學結論必須借助嚴密的邏輯方法進行推理驗證，真正做到有理有據.當然，數學公式、定理、結論等是較為抽象的，學生在證明的過程中可能會遇到一定的障礙，面對學生的障礙，教師不要急于灌輸，而是要適度地進行啟發和點撥，讓學生通過獨立思考和合作探究等方式自主探尋解決問題的方法，突破疑難，以此增強學生學習的信心，提升學生的數學能力.

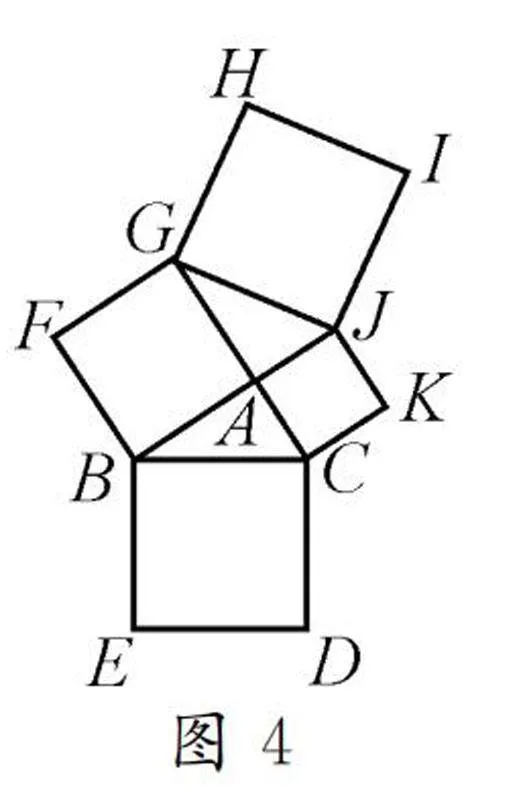
例如，以上環節中，學生通過猜想得到結論后，僅用幾何畫板進行驗證顯然是不具說服力的，為此教師要鼓勵學生用數學語言來表達它，并用數學思維來思考，用數學知識來探究.在以上探究的基礎上，教師繼續追問：如圖4，若△ABC是鈍角三角形，如何證明S+S=2（S+S）？

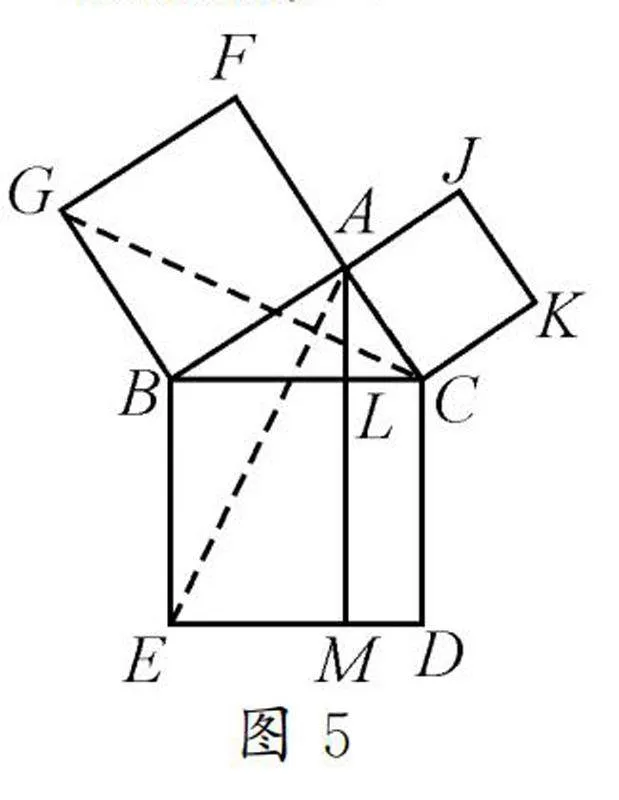
師生活動：問題給出后，教師讓學生獨立證明.該問題較為抽象、復雜，很多學生感覺無從下手.為了幫助學生突破疑難，教師引導學生觀察圖5，并展示歐幾里得證明勾股定理的過程.在這一方法的啟發下，通過師生、生生互動交流，得到證明過程：

設計意圖：教師引導學生利用已有知識、方法進行驗證，充分感悟你增我減、我增你減的平衡美，體驗數學的嚴謹美，點燃學生的探究熱情，提升學生的數學學習興趣.

4 結束語

數學知識具有高度的抽象性，若想學好數學，需要學生具有一定的想象力和數學抽象思維能力.教學中，若教師僅關注知識的講授和題目的訓練，很容易增加數學的枯燥感，從而導致學生產生畏難情緒，影響學習效果.因此在數學教學中，教師要善于從引導學生發現、體會數學之美的角度入手，提供時間和空間讓學生去發現、體驗數學的各種美，如對稱之美、簡潔之美、嚴謹之美等，感悟數學的無限魅力，提升學生的探究興趣，從而讓學生在發現美、探究美的過程中消除枯燥情緒和畏難心理，增強學生的學習信心，提高學生分析、發現和解決問題的能力，促進學生核心素養的落實[1].

在本課的教學中，教師將勾股定理相關知識進行拓展延伸，將直角三角形拓展為銳角三角形和鈍角三角形，以直角三角形為基礎開展一系列的探究活動，讓學生用數學眼光看世界，用數學語言表達世界，用數學思維思考世界，充分體會數學的和諧美、對稱美、簡潔美，充分體驗探究的魅力，感悟特殊到一般的思想方法，提升學生的數學能力與素養.

參考文獻：

[1]田學寧.感受數學之美 提高學習興趣[J].科技創新導報，2015，12（9）：116，118.