高考命題中正態分布的考查熱點

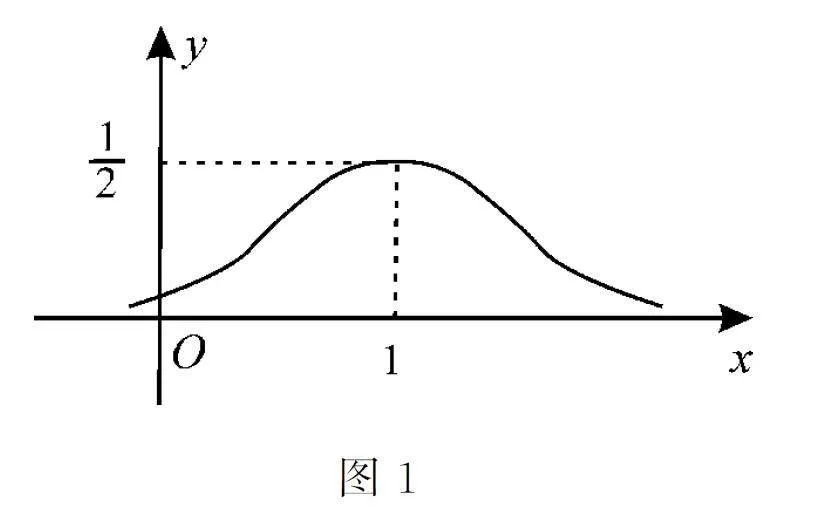
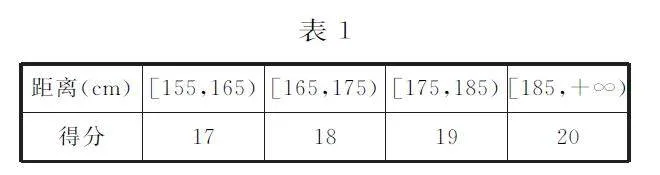
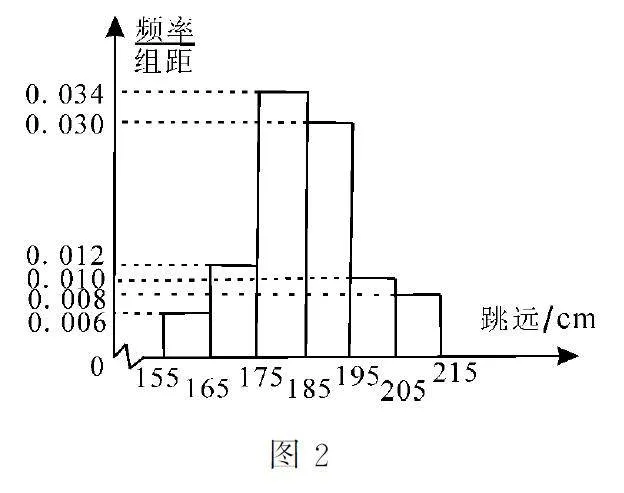
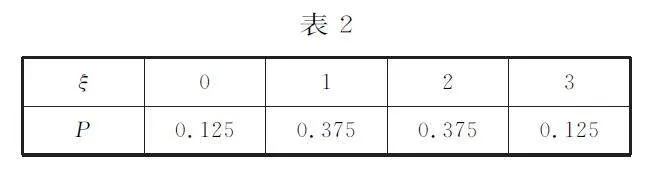
正態分布在自然界中是最常見的一種分布，也是生產、科研和日常生活中經常遇到的一類隨機現象。正態分布在理論研究和實際應用中有著非常重要的價值，也成為高考數學命題的一個重要方向，備受各方關注。

1.參數的確定

例1 （2023年江西省重點中學協作體高考數學第二次聯考數學試卷）某地市在2023年全市一模測試中，全市高三學生數學成績X 服從正態分布N （90，σ2 ），已知P（88

A.0<m <0.34 B.m =0.34

C.0.34<m <0.68 D.m =0.68

分析：根據正態分布所對應的正態函數密度曲線的對稱性，利用正態分布中對應的數據信息，并利用數形結合思想及數學運算來分析與求解。

解：依題意知，X 服從正態分布N （90，σ2），則μ=90。

而P（88<X <92）=0.32，且x=88與x=92關于x=90對稱，所以P （X <85）=m <P（X <88）=1／2[1-P （88<X <92）]=0.34，即0<m <0.34。故選A。

點評：抓住隨機變量的取值所對應的概率，并結合正態函數密度曲線的對稱性，合理構建對應的不等式，是解決問題的關鍵所在。涉及此類參數問題，往往就是回歸正態分布的性質與正態函數密度曲線的幾何特征，從而加以合理邏輯推理與數學運算，使問題得到解決。

2.概率的求解

例2 我們將服從二項分布的隨機變量稱為二項隨機變量，將服從正態分布的隨機變量稱為正態隨機變量。概率論中有一個重要的結論是棣莫弗—拉普拉斯極限定理，它表明，若隨機變量Y ～B （n，p），當n 足夠大時，二項隨機變量Y 可以由正態隨機變量X 來替代，且正態隨機變量X 的期望和方差與二項隨機變量Y 的期望和方差相同。棣莫弗在1733年證明了p=1／2的特殊情形，1812年，拉普拉斯對一般的p 進行了證明。現拋擲一枚質地均勻的硬幣100次，則利用正態分布近似估算硬幣正面向上次數超過60次的概率為（ ）。……