高考物理疑難問題專題突破(３)

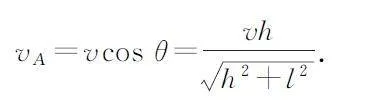
高中階段，功、功率、動能定理、機械能守恒定律及能量守恒定律等知識是高考考查的重點，常結合其他動力學的重點知識進行綜合考查．此類問題通常對學生的運動分析、受力分析及能量轉化分析的能力要求較高，在復習過程中要做到夯實基礎、強化能力、提升素養．本文對功與能專題中學生難以入手且易出錯的幾點疑難問題進行舉例分析，希望能夠幫助學生提高問題解決的能力，提升物理素養．

１ 人做功問題

功是能量轉化的量度，功的計算式W ＝FLcosα中的位移L 是力的作用點的位移．但很多問題中，運動的物體不能看作質點，比如人在原地起跳、爬樓梯、乘扶梯等，涉及人體做功問題時，如果對功的理解不深刻，對功的求解往往會出現錯誤．

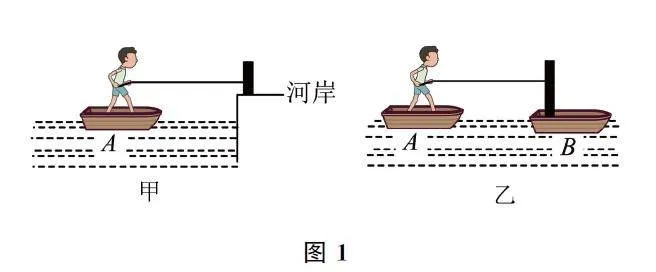
例１ 如圖１所示，在甲、乙兩種情況下，人用同樣大小的恒力拉輕質繩子，使人和船均向右運動，經過相同的時間t，甲中的船A 沒有到岸，乙中的船A沒有與船B 碰撞，則在此過程中（ ）．

A．甲中船A （包括人）的速度比乙中的船A （包括人）的速度大

B．甲中人對繩子的拉力的沖量比乙中人對繩子拉力的沖量小

C．甲中人對繩子的拉力的沖量和乙中人對繩子拉力的沖量一樣大

D．兩種情況下，人做的功一樣多

解析 根據題意，兩幅圖中，拉力等大，作用時間相同，故拉力對繩子的沖量都為I＝Ft，所以沖量一樣大．由動量定理可知，合外力的沖量等于動量的變化，可知船末速度一樣大．兩種情況用同樣大小的力拉繩，船A 向右移動的位移相同，船A 動能增加相同，但乙圖中船B 也要向左移動，船B 動能也增加，故乙圖中拉力做功多，選項C正確．

例２ 自動扶梯以恒定的速度v 運轉，運送人員上樓，一個人第一次站到扶梯上后相對扶梯靜止不動，扶梯載他上樓過程中對他做功為W１，做功功率為P１;第二次該人在運動的扶梯上以相對扶梯的速度v同時勻速向上走，這次扶梯對人做功為W２，做功功率為P２．下列說法正確的是（ ）．

A．W１＞W２，P１＞P２

B．W１＞W２，P１＝P２

C．W１＝W２，P２＞P１

D．W１＝W２，P１＝P２

解析 兩次所用時間不同，第二次用的時間少，力作用的距離短，兩種情況人都處于平衡狀態，電梯所給作用力相等，根據W ＝Fs，可知第一次做功多，即W１＞W２．電梯勻速上行，速度不變，電梯對人的作用力都等于人的重力，根據公式P ＝Fv，可知兩次電梯做功功率相等，即P１＝P２．

小結 以上例題都涉及人做功，利用做功公式W ＝Fs 求解需要深刻理解s 的物理意義，s 指力直接作用在物體上時物體對地的位移．理解這點則以上類似問題可迎刃而解．比如，人原地起跳時，地面對人的作用力是人起跳的動力，由于力直接作用在人的腳上，而腳離地前沒有位移，所以這個力對人并不做功．

拓展 如圖２所示為無窮大水面，水面上有多塊質量為M 、長度為２l 的首尾相連的漂浮的木板．一質量為m 的小孩（可視為質點）在某木板的中央，與該木板一起處于靜止狀態，小孩接下來開始在木板上表演“水上漂”．如果小孩能一次跳離木板（沿板長方向），求小孩第一次跳離木板時做功的最小值．不考慮水與木板接觸面的阻力，設木板質量足夠大且始終處于水面上．

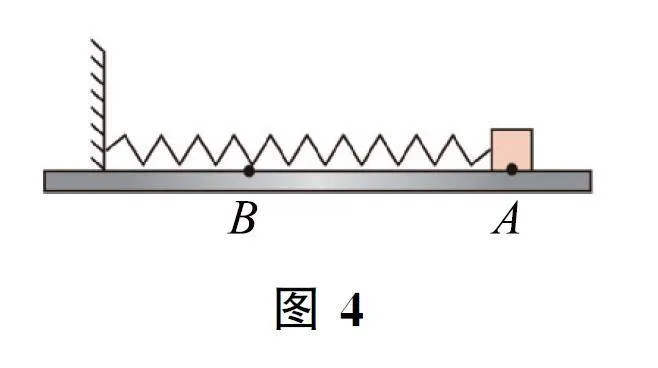
例４ 如圖４所示，水平桌面上的輕質彈簧一端固定，另一端與小物塊相連，彈簧處于自然長度時物塊位于O 點（圖中未標出）．物塊質量m ＝１kg，彈簧勁度系數k＝１００N·m－１，物塊與桌面間的動摩擦因數μ＝０.１．現用水平向右的力將物塊從O 點拉至A點，彈簧伸長量Δx＝１１cm，撤去拉力后物塊由靜止向左運動經O 點最遠到達B 點．重力加速度g 取１０m·s－２．下列說法正確的是（ ）．

A．物塊在B 點所受彈簧彈力與在A 點大小相等

B．物塊運動的總路程為６０.５cm

C．物塊最終停在O 點左側１cm 內某處

D．物塊最終停在O 點左側１cm 處

解析 如果沒有摩擦力，物塊以O 點為平衡位置做簡諧運動，則O 點應該在AB 中間，物塊在B 點所受彈簧彈力與在A 點所受彈簧彈力大小相等，由于有摩擦力，物體從A 到B 過程中有機械能損失，故無法到達沒有摩擦力情況下的“B”點，也即O 點靠近B 點，故物塊在B 點所受彈簧彈力小于在A 點的彈力．物塊最終停止的位置應滿足kx ≤μmg，解得x≤０.０１m＝１cm，即物塊若在O 點左右兩側１cm的范圍內的速度為０，停止運動．

物體從A 到B 過程由能量守恒定律得

１／２k·Δx２＝μmg（x１＋Δx）＋１／２k·x２１，解得x１＝０.０９m＝９cm．

物體從B 點往右運動到O 點右側x２ 過程由能量守恒定律可得１／２k·x２１＝μmg（x１＋x２）＋１／２k·x２２，解得x２＝０.０７m＝７cm．

以此類推，物體再次往左運動到O 點左側x３＝５cm處停止，再往右運動到O 點右側x４＝３cm 處停止，接著再往左運動到O 點左側x５＝１cm 處停止．物塊運動的總路程為。

x總＝Δx＋２x１＋２x２＋２x３＋２x４＋x５＝６０cm，選項D正確．

小結 解決無限往返類的問題，找到規律至關重要．如例３應用動能定理求解路程，找到規律，最后進行數列求和．例４要應用能量守恒定律，通過計算前兩次往復運動的位移規律，確定總路程和停下的位置．這些問題多涉及滑動摩擦力或其他阻力做功，其做功的特點是與路程有關，運用牛頓運動定律及運動學公式將非常煩瑣，甚至無法解出，而動能定理只與物體的初、末狀態有關，所以應用動能定理分析這類問題可使解題過程簡化．

３ 系統機械能守恒問題

對于功和能問題，學生基本能解決單個物體的機械能守恒問題，但對于多物體的系統機械能守恒問題以及非質點類的機械能守恒問題往往會比較難入手．

３．１ 多物體的機械能守恒

在多個物體組成的系統內，若只有動能和勢能的轉化，則系統機械能守恒，解決此類問題關鍵是從三個角度建立關系式．１）能量關系式：系統的機械能守恒，通常選用轉化式（ΔEk＝－ΔEp）或轉移式（ΔEA ＝－ΔEB ）;對系統內的單個物體，一般機械能不守恒，可以應用動能定理．２）位移關系式：根據幾何關系，建立兩個連接物的位移關系式．３）速度關系式：對于同軸轉動的兩物體，根據v＝ωr 建立速度關系式;對于繩（桿）牽連的兩個物體，根據沿繩（桿）方向的分速度相等，建立速度關系式．

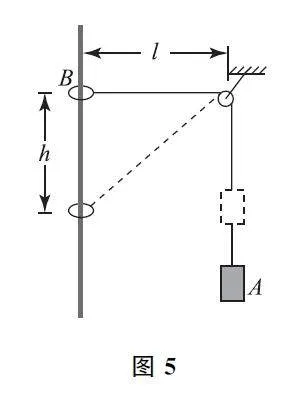
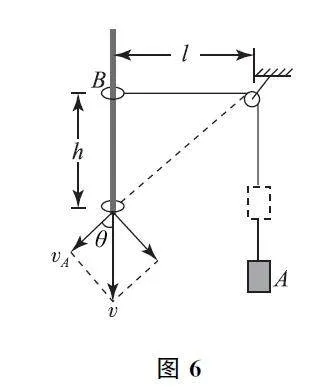
例５ 如圖５所示，物體A 的質量為M ，圓環B的質量為m ，通過繩子連接在一起，圓環套在光滑的豎直桿上，開始時連接圓環的繩子處于水平，長度l＝４m，現從靜止釋放圓環．不計定滑輪和空氣的阻力，g取１０ m·s－２，若圓環下降h ＝３ m 時的速度v ＝５m·s－１，求A 和B 的質量關系．

解析 圓環下降３m 后的速度可以按如圖６所示分解，故可得