基于靜態博弈和遺傳算法的多智能體博弈策略生成方法

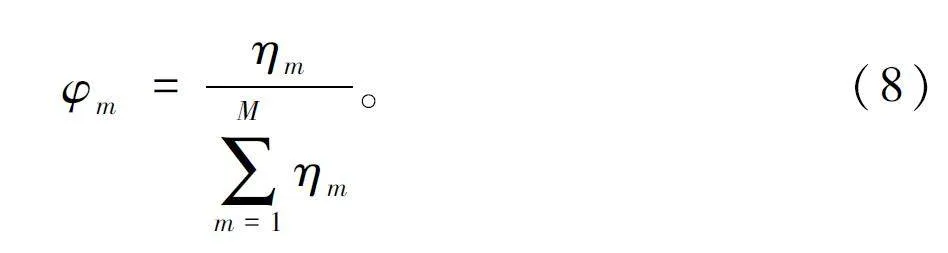
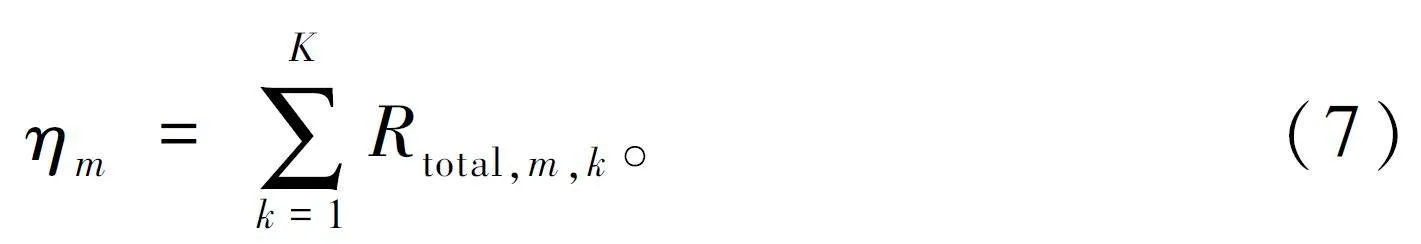
摘 要：在多智能體協同對抗策略生成的過程中，獎勵稀疏和神經網絡參數多易導致策略生成速度慢。針對特定場景如何快速產生對抗策略這一問題，提出了一種基于靜態博弈和遺傳算法的多智能體博弈策略生成方法。基于靜態博弈理念，對馬爾科夫決策過程演化，將策略映射為一串動作組成，簡化策略映射原理；對策略優化問題數學建模。以對抗結果作為目標函數，基于動作集合優化目標函數，通過優化的方法能夠獲得對抗結果最優的策略；給出策略優化框架，并改進遺傳算法實現對于多智能體博弈策略的快速并行尋優。實驗結果表明，相比于經典多智能體強化學習方法，所提方法能夠高效產生多智能體博弈策略。

關鍵詞：靜態博弈；遺傳算法；策略生成

中圖分類號：ＴＮ９２９． ５ 文獻標志碼：Ａ 開放科學（資源服務）標識碼（ＯＳＩＤ）：

文章編號：１００３－３１０６（２０２４）０６－１３５５－０６

０ 引言

隨著人工智能技術的發展，近年來在各控制領域不斷取得亮眼表現，如人機博弈［１］、無人駕駛［２］和智慧醫療［３－４］等。特別是對于多智能體協同管控的現實客觀需求，使得智能策略生成和優化技術快速發展，多智能體博弈策略生成方法成為當前的研究熱點。

在實踐過程中，面臨的典型問題為：對手策略或者環境較為固定的情況下，如何快速生成對抗策略。傳統方法采用強化學習方法通過估計當前狀態的狀態轉移過程和動作分布從而估計出得到最大值獎賞值的策略［５－１０］，如深度Ｑ 網絡（Ｄｅｅｐ Ｑｎｅｔｗｏｒｋ，ＤＱＮ）、Ｓｏｆｔ ＡｃｔｏｒＣｒｉｔｉｃ （ＳＡＣ）。但是，隨著實體個數的增加導致部分可觀測信息和狀態信息的維度增加，神經網絡維度增加，進一步引起神經元參數收斂困難，從而導致神經網絡難訓練引起策略生成和優化失敗。多智能深度強化學習方法被提出用以解決該問題，具有代表性的方法是ＱＭＩＸ［１１］和Ｑｔｒａｎ［１２］等。除此之外，強化學習需要動作具有良好的反饋，但是在工程落地過程中，存在中間態指標多維度高難以最終結果作為目標進行擬合，從而引起在強化學習領域中較難處理的“回報稀疏”問題［１３－１４］，但是從對抗結果衡量策略效果較易實現。如在文獻［１５］中，任務是否成功可以直接通過判斷無人機是否達到指定位置，但是僅依靠終局結果很難對深度神經網絡進行訓練，所以基于課程學習思路引入了遷移性評估指標對獎賞空間在數學表征上進行稠密化［１６］。但是該方法并不通用，原因在于需要對領域知識的深刻理解形成專家知識牽引智能模型進行訓練。故針對特定策略產生對抗策略的關鍵問題在于如何在稀疏獎賞的引導下生成對抗策略。文獻［１７］在雷達探測策略假定的情況下，梳理出智能干擾設備可調整的干擾參數。基于任務目標構建目標函數和約束函數，采用元啟發算法對參數進行優化，從而產生最優對抗策略。該方法對博弈過程采用靜態建模，在整個過程中，雷達在特定模式下初始參數和行為模型固定，所以干擾參數數值求解，并形成靜態對抗策略。但是，在動態博弈過程中，需要通過動作組成策略。策略內的動作間會變化，需要針對動態場景進行改進［１８］。

針對該不足，基于靜態博弈理論［１９］，提出面向動態場景的多智能體博弈策略生成方法。對馬爾科夫決策過程演化，將策略映射為一串動作組成，簡化策略映射原理。將策略優化問題轉化為數學尋優問題。以對抗結果作為目標函數，基于動作集合優化目標函數，獲得對抗結果最優的策略。除此之外，構建并行優化框架，改進遺傳算法實現對于多智能體博弈策略的快速并行尋優［２０］。實驗結果表明，相比于經典多智能體強化學習方法，本方法能夠高效產生多智能體博弈策略。

本文余下內容結構組織如下：第１ 節詳細推導并闡述基于靜態博弈理論的策略優化模型，為后續第２ 節提出的方法奠定了基礎，并在第３ 節通過實驗驗證本方法的有效性，最后總結全文。

１ 基于靜態博弈理論的策略優化模型

基于博弈論，策略π 是由一系列動作ａ 構成的。

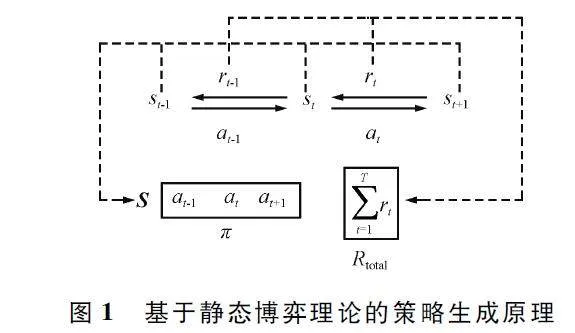
馬爾科夫決策過程的本質也是在數學上尋找到由狀態ｓｔ 到ａｔ 的映射過程，其中ｓｔ ∈Ｓ，Ｓ 為狀態空間；ａｔ∈Ａ，Ａ 為動作空間。在針對特定策略這一假設前提下，對手策略的狀態動作映射較為固定。對手策略的狀態動作映射可以弱化為策略標簽，用于區分不同對手策略。進一步，可以弱化對于對手狀態ｓｔ 的特征提取過程，使策略π 直接施加于對手策略上，通過對抗結果進行反饋。上述演進過程如圖１ 所示。

從最優化角度分析可知，對手策略和博弈環境可以固定為博弈函數ｆ，策略博弈產生結果的過程可以表述為：

Ｒｔｏｔａｌ ＝ ｆ（π）， （１）

式中：Ｒｔｏｔａｌ 為總獎賞。

Ｒｔｏｔａｌ ＝ ΣＴｔ ＝ １ｒｔ。（２）

在典型對抗環境中，中間獎賞較難獲得，需要通過獎賞塑形等大量的專業領域才能構成，所以最直觀為采用最終結果作為獎賞：

Ｒｔｏｔａｌ ＝ ｒＴ 。（３）

最優策略即為使得博弈函數最大的策略，即優化目標為：

π* ＝ ａｒｇｍａｘ π ｆ（π）， （４）

式中：π 為由一系列動作構成的策略，π 為所有可能的動作組合成的策略集合，π 為最優策略。

該模型的優勢在于能夠有效地解決獎賞稀疏的問題。在智能決策應用場景中，通過結果設計獎賞函數較為容易，如將目標擊毀個數轉化為獎賞分值［１５］。但是，在博弈過程中，通過結果設計獎賞會使得大部分時間沒有獎賞值，無法預測獎賞值出現時間，無法準確評估動作的有效性，指引策略的收斂方向。而采用領域知識可以使得獎賞稠密，如將智能體與目標之間的距離或者將抗干擾跳頻時選擇的信道間隔轉化為獎賞值［１５，１８］，有助于策略加速收斂。但是，需要領域專家根據場景需求設計，容易引入主觀因素導致收斂在局部最優策略。所以，針對上述矛盾，依據靜態博弈理論，在獎賞稀疏的假設前提條件下，將馬爾科夫決策過程演化為靜態優化問題，明確目標函數，將策略優化問題完全數學化表征，使得策略可以通過數學優化方法進行求解，規避了馬爾科夫決策過程在獎賞稀疏條件下策略生成困難的弊端。

２ 基于遺傳算法的策略生成方法

得益于在理論層面將動態博弈問題簡化為了優化問題，使得采用遺傳算法能夠快速找出博弈過程中的最優動作排序，并將其映射為策略，從而實現針對特定策略的快速生成。但是，對于遺傳算法而言，其計算量大且耗時的部分在于需要計算種群中每個個體的適應度，故提出并行優化框架對方法進行加速。后續本節分為兩部分，詳細闡述基于遺傳算法的策略生成方法，分別為并行求解框架和優化方法。

２． １ 并行優化框架

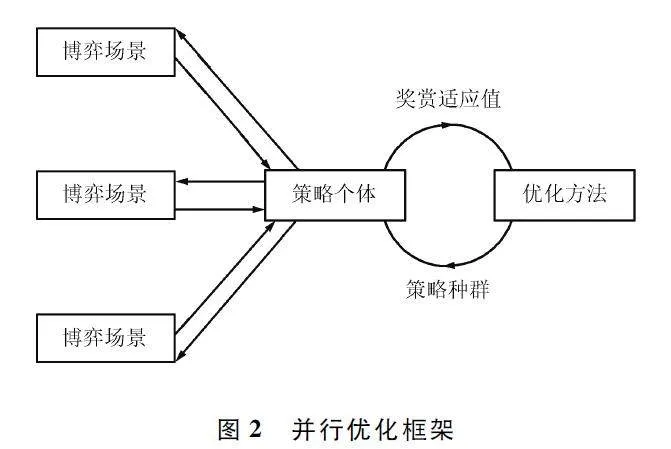
并行優化框架如圖２ 所示。整個并行優化過程闡述如下：首先，構建由一系列動作作為基因組成策略個體，再將多個策略個體組成策略種群。在該階段，需要根據對抗時長和受控體的個數相乘得到策略個體中包含的動作基因個數。然后，每一個策略個體在博弈場景中與對手策略對抗，將獎賞作為每個策略個體的適應值返回。在此過程中，利用并行進行多個策略個體的對抗，能夠快速獲得。最后，將策略種群和個體依次對應的獎賞適應值傳入優化方法。優化方法過濾并生成新的策略種群，并進入下一次策略優化環路。由基于靜態博弈理論的策略生成數學優化模型一節的數學分析過程可以看出，作為核心理論，其在實施層面具有良好的并行化能力，從而使得并行化框架的構建成為可能，并將結合硬件算力大幅度提升策略優化的性能。

２． ２ 優化方法

在優化過程中，需要完成策略的數學化表達。假設在多智能體對抗環境中，智能體個數為Ｎ，在博弈期間需要執行動作次數為Ｔ，每次執行離散動作。故策略個體π 由Ｎ×Ｔ 個動作基因組成，即：

π ＝ ［ａ１ ，ａ２ ，…，ａＴ ］ＮＴ 。（５）

當策略種群由Ｍ 個策略個體組成時，策略種群π 可以表示為：

π ＝ ［π１ ，π２ ，…，πＭ ］Ｍ ×ＮＴ 。（６）

構建多個線程Ｌ，線程之間相互獨立。針對不同策略個體的開展Ｋ 次博弈對抗，得到與個體相對應的獎賞適應值：

當所有策略個體對應的獎賞適應值計算運行完成后，按照獎賞適應度由高到低，對策略種群π 中的策略個體π 排序。

根據策略種群π 獎賞適應值進行個體獎賞適應值的歸一化，對于第ｍ 個策略個體π，其種群選擇概率為：

根據個體策略的獎賞適應值對種群進行過濾，保留指定數量Ｍ′個獎賞適應值排名靠前的策略個體。除此之外，在剩余策略個體中，隨機抽取２ 個策略個體進行拼接形成新策略個體并放回種群中，該過程可以通過數學表達為：

π′１ ＝ ［π１ ［１：ｔ′］，π２ ［ｔ′ ＋ １：Ｔ］］， （９）

π′２ ＝ ［π２ ［１：ｔ′］，π１ ［ｔ′ ＋ １：Ｔ］］， （１０）

式中：π１ 和 π２ 為隨機抽取出的策略個體，π１′和 π２′為拼接后的策略個體，ｔ′為隨機生成的拼接位置，ｔ′∈ＮＴ，隨機概率門限為ε１ 。

為了進一步提高策略種群的搜索能力，對種群中的個體進行動作基因突變操作。遍歷新生成策略種群中每個動作基因，以概率門限為ε２ 為基礎進行隨機變異。當超過變異門限時，從可選動作范圍內隨機選擇一個離散動作進行替換。

經過上述過程的迭代，最終即可獲得最優策略個體和其對應的最優獎賞適應值。

３ 實驗驗證

實驗驗證由實驗場景、實驗設計、參數設置和結果分析四部分組成。

３． １ 實驗場景

為了能夠有效驗證本方法的有效性，采用ＤｅｅｐＭｉｎｄ 和暴雪公司開發的基于“星際爭霸２”的多智能體對抗環境（ＳｔａｒＣｒａｆｔ ＭｕｌｔｉＡｇｅｎｔ Ｃｈａｌｌｅｎｇｅ，ＳＭＡＣ）進行實驗［２１］。ＳＭＡＣ 內置基線對抗策略，用于驗證策略效果。除此之外，由于典型用于多智能體策略對抗的深度強化學習需要對應場景進行超參數調整，該典型場景公認性較高，故均基于此環境進行開發和調試，其對照算法的超參數可以直接獲得。采用ＳＭＡＣ 環境中名稱為“３ｍ”的多智能體同構場景進行驗證。

３． ２ 實驗設計

實驗過程共設置步長為１０６ ，分為訓練階段和評估階段，以５ ０００ 步為周期循環。在訓練階段，設置種群訓練門限為５ ０００ 步。在該階段內，對種群內個體進行適應度并行計算和交叉變異。當每種群運行步數超過５ ０００ 步進行一次性能評估。在性能評估階段，與基線策略對抗２４ 回合。衡量對抗策略的有效性，最根本在于評估勝率，故在實驗中用勝率作為評估指標。對于勝率而言，計算２４ 回合內與“３ｍ”場景的基線策略對抗獲勝的次數，再除以總回合數得到勝率。除此之外，在實驗過程中，將ＱＭＩＸ和ＶａｌｕｅＤｅｃｏｍｐｏｓｉｔｉｏｎ Ｎｅｔｗｏｒｋｓ （ＶＤＮ ）方法在“３ｍ”場景中的勝率和平均獎賞作為對照組，驗證本方法的性能。除此之外，ＶＤＮ 和ＱＭＩＸ 方法分別使用以結果作為獎賞的非獎賞塑形和ＳＭＡＣ 環境提供的獎賞塑形。在判斷勝負的基礎上，ＳＭＡＣ 環境提供的塑形獎賞通過受控體之間的位置關系和生命值等特征構建了獎賞函數。通過設置對照實驗，用于展示獎賞稀疏對于典型算法的影響，突出該問題解決的必要性，并驗證了本方法在解決該問題上的有效性。

３． ３ 參數設置

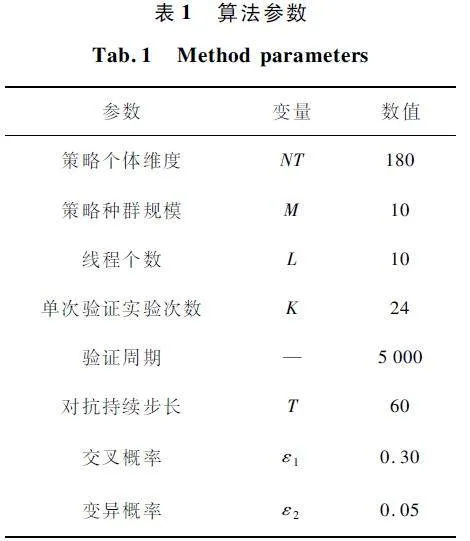
本文實驗所用到的算法參數如下表１ 所示。

３． ４ 結果分析

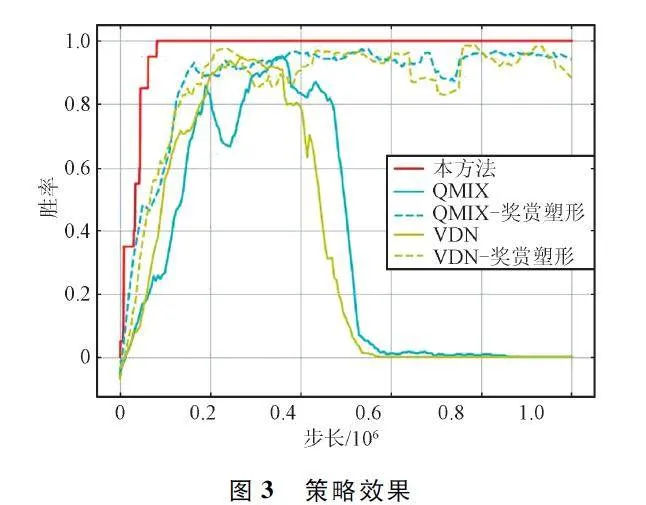
策略效果如圖３ 所示，展示了本方法、ＶＤＮ 和ＱＭＩＸ 隨訓練步長增加的勝率變化趨勢。在圖３中，“ＶＤＮ－獎賞塑形”和“ＱＭＩＸ－獎賞塑形”表示采用ＳＭＡＣ 提供的獎賞塑形進行訓練得到的博弈策略，而ＶＤＮ 和ＱＭＩＸ 表示僅通過勝負關系構建獎賞得到的博弈策略。從對比采用獎賞塑形和非獎賞塑形的２ 種方法可以看出，采用獎賞塑形的方法勝率提升趨勢較為穩定，而采用非獎賞塑形的由于獎賞反饋稀疏，在實驗初期勝率提升較慢，且在實驗中后期出現明顯的勝率衰退現象。雖然通過保存最大勝率對應的神經網絡參數的方法使其不至于出現嚴重衰退，但是勝率無法與塑形獎賞相比。相比之下，雖然本文方法、“ＶＤＮ －獎賞塑形”和“ＱＭＩＸ －獎賞塑形”都能夠達到最大勝率，但是本文方法速度快且穩定，且能夠有效避免由于獎賞稀疏導致的性能衰退。

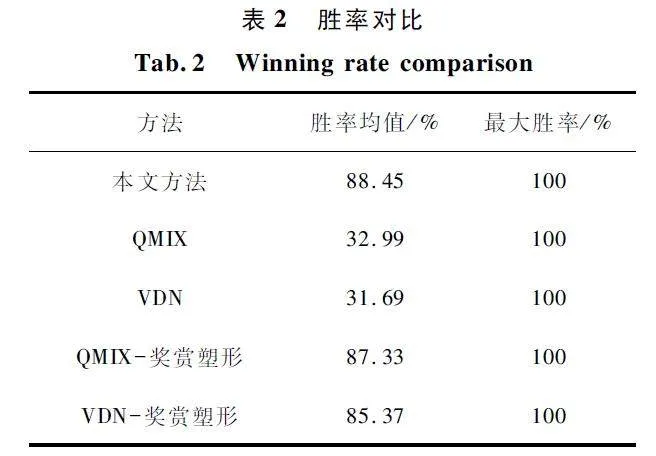
為了進一步量化對比方法性能，對５ 種方法的勝率求取均值和最大值，如表２ 所示。５ 種方法均能夠達到最大勝率，但是通過勝率均值可以發現，本文方法相比于其他方法的勝率均值最大，表明本文方法相對穩定。

綜合圖３ 和表２ 的勝率趨勢和量化勝率，可見本文方法在針對特定對手策略時，在獎賞稀疏的情況下，能夠快速且穩定地生成對抗策略。

４ 結束語

針對特定策略如何快速產生對抗策略這一問題，結合博弈論中的靜態博弈理論和遺傳算法，提出了一種改進的多智能體博弈策略生成方法。在理論層面，基于靜態博弈理念，對馬爾科夫決策過程演化，將策略映射為一串動作組成，簡化策略映射原理。在理論基礎上，對策略優化問題數學建模。以對抗結果作為目標函數，基于動作集合優化目標函數，通過優化的方法能夠獲得對抗結果最優的策略。在實現層面，設計策略優化框架，并改進遺傳算法實現對于多智能體博弈策略的快速并行尋優。在實驗中，將典型多智能體強化學習方法作為基線，通過與基線方法對比，表明了本方法產生策略的高效性，并且展現了本文方法基于并行方法能夠有效提高策略生成與優化速度。

參考文獻

［１］ ＭＮＩＨ Ｖ，ＫＡＶＵＫＣＵＯＧＬＵ Ｋ，ＳＩＬＶＥＲ Ｄ，ｅｔ ａｌ． ＨｕｍａｎＬｅｖｅｌ Ｃｏｎｔｒｏｌ ｔｈｒｏｕｇｈ Ｄｅｅｐ Ｒｅｉｎｆｏｒｃｅｍｅｎｔ Ｌｅａｒｎｉｎｇ［Ｊ］．Ｎａｔｕｒｅ，２０１５，５１８：５２９－５３３．

［２］ ＦＥＮＧ Ｓ，ＳＵＮ Ｈ Ｗ，ＹＡＮ Ｘ Ｔ，ｅｔ ａｌ． Ｄｅｎｓｅ ＲｅｉｎｆｏｒｃｅｍｅｎｔＬｅａｒｎｉｎｇ ｆｏｒ Ｓａｆｅｔｙ Ｖａｌｉｄａｔｉｏｎ ｏｆ Ａｕｔｏｎｏｍｏｕｓ Ｖｅｈｉｃｌｅｓ［Ｊ］． Ｎａｔｕｒｅ，２０２３，６１５：６２０－６２７．

［３］ ＺＨＵ Ｙ，ＬＩＡＮＧ Ｘ Ｆ，ＷＡＮＧ Ｔ Ｔ，ｅｔ ａｌ． ＭｕｌｔｉｉｎｆｏｒｍａｔｉｏｎＦｕｓｉｏｎ Ｆａｕｌｔ Ｄｉａｇｎｏｓｉｓ ｏｆ Ｂｏｇｉｅ Ｂｅａｒｉｎｇ ｕｎｄｅｒ Ｓｍａｌｌ Ｓａｍｐｌｅｓ ｖｉａ Ｕｎｓｕｐｅｒｖｉｓｅｄ Ｒｅｐｒｅｓｅｎｔａｔｉｏｎ Ａｌｉｇｎｍｅｎｔ Ｄｅｅｐ Ｑｌｅａｒｎｉｎｇ ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｉｎｓｔｒｕｍｅｎｔａｔｉｏｎ ａｎｄＭｅａｓｕｒｅｍｅｎｔ，２０２２，７２：３５０３３１５．

［４］ ＺＨＵ Ｍ Ｘ，ＺＨＵ Ｈ Ｇ． Ｌｅａｒｎｉｎｇ ａ Ｄｉａｇｎｏｓｔｉｃ Ｓｔｒａｔｅｇｙ ｏｎＭｅｄｉｃａｌ Ｄａｔａ ｗｉｔｈ Ｄｅｅｐ Ｒｅｉｎｆｏｒｃｅｍｅｎｔ Ｌｅａｒｎｉｎｇ ［Ｊ ］．ＩＥＥＥ Ａｃｃｅｓｓ，２０２１，９：８４１２２－８４１３３．

［５］ ＭＮＩＨ Ｖ，ＫＡＶＵＫＣＵＯＧＬＵ Ｋ，ＳＩＬＶＥＲ Ｄ，ｅｔ ａｌ． ＰｌａｙｉｎｇＡｔａｒｉ ｗｉｔｈ Ｄｅｅｐ ＲｅｉｎｆｏｒｃｅｍｅｎｔＬｅａｒｎｉｎｇ ［ＥＢ ／ ＯＬ ］．（２０１３－１２－１９）［２０２４－０３－０６］． ｈｔｔｐｓ：∥ａｒｘｉｖ． ｏｒｇ ／ ａｂｓ ／１３１２． ５６０２．

［６］ ＨＡＳＳＥＬＴ Ｈ Ｖ，ＧＵＥＺ Ａ，ＳＩＬＶＥＲ Ｄ． Ｄｅｅｐ ＲｅｉｎｆｏｒｃｅｍｅｎｔＬｅａｒｎｉｎｇ ｗｉｔｈ Ｄｏｕｂｌｅ Ｑｌｅａｒｎｉｎｇ ［Ｃ］∥ Ｐｒｏｃｅｄｉｎｇ ｏｆ ｔｈｅＴｈｉｒｔｉｅｔｈ ＡＡＡＩ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ａｒｔｉｆｉｃａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ． Ｐｈｏｅｎｉｘ：ＡＡＡＩ Ｐｒｅｓｓ，２０１６：２０９４－２１００．

［７］ ＳＣＨＡＵＬ Ｔ，ＱＵＡＮ Ｊ，ＡＮＴＯＮＯＧＬＯＵ Ｉ，ｅｔ ａｌ． ＰｒｉｏｒｉｔｉｚｅｄＥｘｐｅｒｉｅｎｃｅ Ｒｅｐｌａｙ［ＥＢ ／ ＯＬ］． （２０１５ － １１ － １８ ）［２０２４ －０３－０６］． ｈｔｔｐｓ：∥ａｒｘｉｖ． ｏｒｇ ／ ａｂｓ ／ １５１１． ０５９５２．

［８］ ＨＡＡＲＮＯＪＡ Ｔ，ＺＨＯＵ Ａ，ＡＢＢＥＥｌ Ｐ，ｅｔ ａｌ． Ｓｏｆｔ Ａｃｔｏｒｃｒｉｔｉｃ：Ｏｆｆｐｏｌｉｃｙ Ｍａｘｉｍｕｍ Ｅｎｔｒｏｐｙ Ｄｅｅｐ ＲｅｉｎｆｏｒｃｅｍｅｎｔＬｅａｒｎｉｎｇ ｗｉｔｈ ａ Ｓｔｏｃｈａｓｔｉｃ Ａｃｔｏｒ［ＥＢ ／ ＯＬ］． （２０１８ － ０１ －０４）［２０２４－０３－０６］． ｈｔｔｐｓ：∥ａｒＸｉｖ：１８０１． ０１２９０ｖ２．

［９］ ＨＡＡＲＮＯＪＡ Ｔ，ＺＨＯＵ Ａ，ＨＡＲＴＩＫＡＩＮＥＮ Ｋ，ｅｔ ａｌ． ＳｏｆｔＡｃｔｏｒｃｒｉｔｉｃ Ａｌｇｏｒｉｔｈｍｓ ａｎｄ Ａｐｐｌｉｃａｔｉｏｎｓ［ＥＢ／ ＯＬ］． （２０１８－１２－１３）［２０２３－０９－０６］． ｈｔｔｐｓ：∥ ａｒＸｉｖ：１７０７． ０６３４７ｖ２．

［１０］ ＷＡＮＧ Ｚ Ｙ，ＳＣＨＡＵＬ Ｔ，ＨＥＳＳＥＬ Ｍ，ｅｔ ａｌ． Ｄｕｅｌｉｎｇ ＮｅｔｗｏｒｋＡｒｃｈｉｔｅｃｔｕｒｅｓ ｆｏｒ Ｄｅｅｐ Ｒｅｉｎｆｏｒｃｅｍｅｎｔ Ｌｅａｒｎｉｎｇ ［Ｃ］∥Ｐｒｏｃｅｅｄｉｎｇ ｏｆ ｔｈｅ ３３ｒｄ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ ＭａｃｈｉｎｅＬｅａｒｎｉｎｇ． Ｎｅｗ Ｙｏｒｋ：ＪＭＬＲ． ｏｒｇ，２０１６：１９９５－２００３．

［１１］ＲＡＳＨＩＤ Ｔ，ＳＡＭＶＥＬＹＡＮ Ｍ，ＷＩＴＴ Ｃ Ｓ Ｄ，ｅｔ ａｌ． ＭｏｎｏｔｏｎｉｃＶａｌｕｅ Ｆｕｎｃｔｉｏｎ Ｆａｃｔｏｒｉｓａｔｉｏｎ ｆｏｒ Ｄｅｅｐ Ｍｕｌｔｉａｇｅｎｔ Ｒｅｉｎｆｏｒｃｅｍｅｎｔ Ｌｅａｒｎｉｎｇ ［Ｊ］． Ｊｏｕｒｎａｌ ｏｆ Ｍａｃｈｉｎｅ Ｌｅａｒｎｉｎｇ Ｒｅｓｅａｒｃｈ，２０２０，２１（１）：７２３４－７２８４．

［１２］ＳＯＮ Ｋ，ＫＩＭ Ｄ，ＫＡＮＧ Ｗ Ｊ，ｅｔ ａｌ． ＱＴＲＡＮ：Ｌｅａｒｎｉｎｇ ｔｏ Ｆａｃｔｏｒｉｚｅ ｗｉｔｈ Ｔｒａｎｓｆｏｒｍａｔｉｏｎ ｆｏｒ Ｃｏｏｐｅｒａｔｉｖｅ Ｍｕｌｔｉａｇｅｎｔ Ｒｅｉｎｆｏｒｃｅｍｅｎｔ Ｌｅａｒｎｉｎｇ ［ＥＢ／ ＯＬ］． （２０１９ －０５ －１４）［２０２４ －０３ －０６］． ｈｔｔｐ：∥ａｒＸｉｖ． ｏｒｇ／ ａｂｓ／ １９０５． ０５４０８．

［１３］ＷＡＮＧ Ｘ，ＣＨＥＮ Ｙ Ｄ，ＺＨＵ Ｗ Ｗ． Ａ Ｓｕｒｖｅｙ ｏｎ ＣｕｒｒｉｃｕｌｕｍＬｅａｒｎｉｎｇ ［Ｊ］． ＩＥＥＥ Ｔｒａｎｓａｃｔｉｏｎｓ ｏｎ Ｐａｔｔｅｒｎ Ａｎａｌｙｓｉｓ ａｎｄＭａｃｈｉｎｅ Ｉｎｔｅｌｌｉｇｅｎｃｅ，２０２２，４４（９）：４５５５－４５７６．

［１４］ ＯＫＵＤＯ Ｔ，ＹＡＭＡＤＡ Ｓ． Ｌｅａｒｎｉｎｇ Ｐｏｔｅｎｔｉａｌ ｉｎ Ｓｕｂｇｏａｌｂａｓｅｄ Ｒｅｗａｒｄ Ｓｈａｐｉｎｇ ［Ｊ ］． ＩＥＥＥ Ａｃｃｅｓｓ，２０２３，１１：１７１１６－１７１３７．

［１５］ 暢鑫，李艷斌，趙研，等． 基于ＭＡ２ＩＤＤＰＧ 算法的異構多無人機協同突防方法［Ｊ］． 河北工業科技，２０２２，３９（４）：３２８－３３４．

［１６］ ＹＩＮ Ｈ，ＧＵＯ Ｓ Ｘ，ＬＩ Ａ，ｅｔ ａｌ． Ａ Ｄｅｅｐ ＲｅｉｎｆｏｒｃｅｍｅｎｔＬｅａｒｎｉｎｇｂａｓｅｄ Ｄｅｃｅｎｔｒａｌｉｚｅｄ Ｈｉｅｒａｒｃｈｉｃａｌ Ｍｏｔｉｏｎ ＣｏｎｔｒｏｌＳｔｒａｔｅｇｙ ｆｏｒ Ｍｕｌｔｉｐｌｅ Ａｍｐｈｉｂｉｏｕｓ Ｓｐｈｅｒｉｃａｌ Ｒｏｂｏｔ Ｓｙｓｔｅｍｓｗｉｔｈ Ｔｉｌｔｉｎｇ Ｔｈｒｕｓｔｅｒｓ ［Ｊ］． ＩＥＥＥ Ｓｅｎｓｏｒｓ Ｊｏｕｒｎａｌ，２０２４，２４（１）：７６９－７７９．

［１７］ ＣＨＡＮＧ Ｘ，ＬＩ Ｙ Ｂ，ＺＨＡＯ Ｙ，ｅｔ ａｌ． Ａ ＭｕｌｔｉｐｌｅｊａｍｍｅｒＤｅｃｅｐｔｉｖｅ Ｊａｍｍｉｎｇ Ｍｅｔｈｏｄ Ｂａｓｅｄ ｏｎ Ｐａｒｔｉｃｌｅ Ｓｗａｒｍ Ｏｐｔｉｍｉｚａｔｉｏｎ ａｇａｉｎｓｔ Ｔｈｒｅｅｃｈａｎｎｅｌ ＳＡＲ ＧＭＴＩ ［Ｊ］． ＩＥＥＥＡｃｃｅｓｓ，２０２１，９：１３８３８５－１３８３９３．

［１８］ ＬＩＵ Ｓ Ｙ，ＸＵ Ｙ Ｆ，ＣＨＥＮ Ｘ Ｑ，ｅｔ ａｌ． Ｐａｔｔｅｒｎａｗａｒｅ Ｉｎｔｅｌｌｉｇｅｎｔ Ａｎｔｉｊａｍｍｉｎｇ Ｃｏｍｍｕｎｉｃａｔｉｏｎ：Ａ Ｓｅｑｕｅｎｔｉａｌ ＤｅｅｐＲｅｉｎｆｏｒｃｅｍｅｎｔ Ｌｅａｒｎｉｎｇ Ａｐｐｒｏａｃｈ ［Ｊ ］． ＩＥＥＥ Ａｃｃｅｓｓ，２０１９，７：１６９２０４－１６９２１６．

［１９］ 阿維亞德·海菲茲． 博弈論［Ｍ］． 劉勇，譯． 上海：上海人民出版社，２０１５．

［２０］ ＥＮＧＥＬＢＲＥＣＨＴＡ Ｐ． Ｃｏｍｐｕｔａｔｉｏｎａｌ Ｉｎｔｅｌｌｉｇｅｎｃｅ：Ａｎ Ｉｎｔｒｏｄｕｃｔｉｏｎ［Ｍ］． Ｎｅｗ Ｊｅｒｓｅｙ：Ｗｉｌｅｙ，２００７．

［２１］ ＳＡＭＶＥＬＹＡＮ Ｍ，ＲＡＳＨＩＤ Ｔ，ＷＩＴＴ Ｃ Ｓ Ｄ，ｅｔ ａｌ． ＴｈｅＳｔａｒＣｒａｆｔ Ｍｕｌｔｉａｇｅｎｔ Ｃｈａｌｌｅｎｇｅ［Ｃ］∥ Ｐｒｏｃｅｅｄｉｎｇｓ ｏｆ ｔｈｅ１８ｔｈ Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｃｏｎｆｅｒｅｎｃｅ ｏｎ Ａｕｔｏｎｏｍｏｕｓ Ａｇｅｎｔｓ ａｎｄＭｕｌｔｉ Ａｇｅｎｔ Ｓｙｓｔｅｍｓ． Ｍｏｎｔｒｅａｌ：Ｉｎｔｅｒｎａｔｉｏｎａｌ Ｆｏｕｎｄｕｔｉｏｎｆｏｒ Ａｕｔｏｎｏｍｏｕｓ Ａｇｅｎｔｓ ａｎｄ Ｍｕｌｔｉａｇｅｎｔ Ｓｙｓｔｅｍｓ，２０１９：２１８６－２１８８．

作者簡介

劉東輝 女，（１９９０—），博士，講師。主要研究方向：復雜系統管理、策略優化等。

鄭贏營 女，（１９９８—），碩士研究生。主要研究方向：復雜系統管理。

暢 鑫 男，（１９９０—），博士，高級工程師。

基金項目：國家自然科學基金（７１９９１４８５，７１９９１４８１，７１９９１４８０）；中國博士后科學基金（２０２１Ｍ６９３００２）