微分幾何的直觀性、研究性教學

2024-09-15 00:00:00景麗

科技風 2024年26期

摘要：微分幾何研究空間曲線與曲面，研究對象復雜，目前課程沒能提供幾何直觀分析，這導致實際課程教學比較抽象，學生難以把握一些基本概念、結論等；另外課程缺少研究性、探究性教與學。本文首先研究《微分幾何》課程教學的直觀性問題，針對課程中密切面、撓率和曲率線基本概念、空間曲線和曲面一點的鄰近結構基本結論，給出具體實例，使用軟件MATLAB編寫程序，提供幾何直觀圖像。其次，給出探究性教學案例。文中提供的程序、圖像能增強教學的直觀性，探究性案例有利于開展研究性教學。

關鍵詞：微分幾何; 直觀教學;研究性教學；MATLAB

文獻標識碼： A 中圖分類號： G642; O186.1

1 概述

微分幾何不僅是現代數學重要的研究方向，它也有許多科學與實際應用，如極小曲面被應用在現代建筑外形設計上[1]，飛機等機器部件的設計研究離不開微分幾何[2-3]，測地線理論被應用到大地測量等[4]；微分幾何在自動控制、人工智能領域也應用廣泛[5-10]；高斯-博內公式更可以幫助人們認識羅氏幾何等，促進人們對非歐幾何、現代幾何學的理解[11]。

本科《微分幾何》課程是一門重要的基礎課，它承擔傳授微分幾何基本概念、思想和方法的任務，不僅如此，它還是解析幾何、高等代數、數學分析和常微分方程在其中廣泛應用的學科，提高《微分幾何》課程教學質量，可以促進學生綜合知識與能力的提升。然而實際

教學使筆者感受到《微分幾何》課程急需增強直觀性、研究性教學，《微分幾何》研究空間曲線與曲面，研究對象復雜，如果缺乏曲線、曲面等的直觀圖形，一些基本概念難以被真正理解；例如學生很難理解撓率概念，教師也不易描述它；另外學生也許能求出某曲面的曲率線，但是它在曲面的什么位置問題不易被回答，實際教學處于過于抽象的狀態。如果能加強直觀性、研究性教學，能使當前教學得到明顯改觀。目前關于《微分幾何》直觀教學、研究性教學成果很少見。文獻[12]運用 Matlab 軟件繪制了圓柱螺線、環面等空間圖形，計算了橢圓和擺線的相對曲率，證明了雙曲螺線的曲率和撓率相等，另外計算拋物面的第一基本量、第二基本量及法曲率和主曲率；文獻[13]運用 Matlab繪制了球面、正螺面和麥比烏斯帶等曲面，編程計算了向量函數的導數和極限，曲線弧長，曲線的曲率與撓率等。上述文獻研究成果一定程度上加強了微分幾何教學的直觀性。本文首先深入探討微分幾何的直觀教學問題，通過合理設計圖形并用Matlab加以繪制，以揭示密切面、撓率、曲率線等概念本質，講清空間曲線一點結構以及曲面一點的結構等重要內容，本文將給出相應的程序，為微分幾何的直觀教學提供幫助；另外給出研究性教學案例。

2 基本概念的直觀教學

2.1密切面

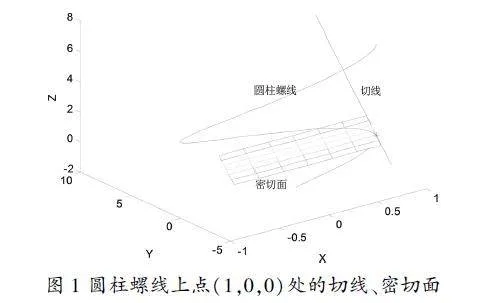
設類的空間曲線，其一點處的密切面是與其最貼近的切平面。密切面由曲線的一階及二級導數張成；也可以由曲線在該點的切向量和主法向量張成[ 14]。例1可以幫助我們理解密切面這一概念。

例1 設圓柱螺線，（1）繪制該曲線；（2）繪制點處的切線及密切面。

t=-1.5：0.2：2*pi;plot3（cos（t），sin（t），t，'r'）%畫圓柱螺線

hold on;x=ones（1，size（t，2））;

plot3（x，t，t）%繪制圓柱螺線在點（1，0，0）處的切線

plot3（1，0，0，'b*'）

[X，Y]=meshgrid（-0.5：0.25：1）;%繪制圓柱螺線在點（1，0，0）處的密切面

Z=Y;mesh（X，Y，Z）

程序的運行結果如圖1，從圖1可以清楚地看到密切面與圓柱螺線的緊密貼合。

2.2 撓率

直觀地講，撓率就是曲線離開密切面的程度[14].圖1清楚地顯示了圓柱螺線在點離開密切面的程度，圖1可以幫助我們理解撓率概念。

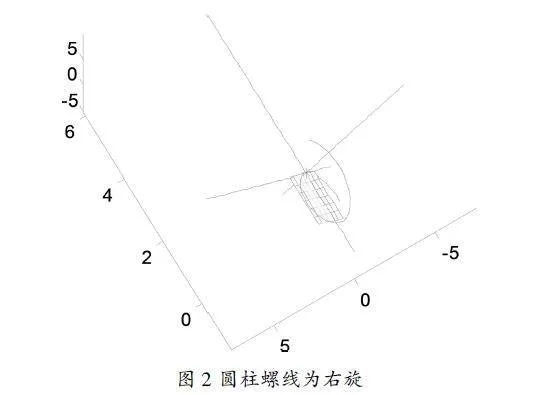
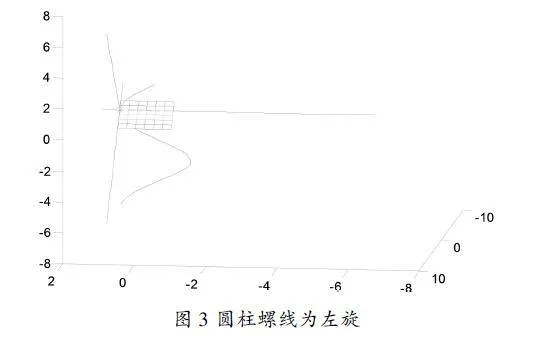
對于撓率的認識不能僅限于此，撓率還決定曲線一點鄰近的結構。對于圓柱螺線來說，當撓率時是右旋的，螺距向上延伸；當撓率時是左旋的，螺距向下延伸，分別如圖2_1、圖2_2.

撓率也可以準確地計算。設類的空間曲線，撓率計算公式為[ 15]：

圓柱螺線的撓率是常數，例2程序用以說明這一結果。

例2 計算圓柱螺線在點處的撓率。

syms t;s=0;r=[cos（t），sin（t），t];r1=diff（r）;r1_1=subs（r1，'t'，s）;

r2=diff（r1）;r2_1=subs（r2，'t'，s）;r3=diff（r2）;r3_1=subs（r3，'t'，s）;

naolv=det（[r1_1;r2_1;r3_1]）/（norm（cross（r1_1，r2_1）））^2

運行結果：0.5.

2.3 曲率線

曲率線是曲面上的一條曲線，如果該曲線每點的切方向都是主方向，則該曲線是曲率線。曲率線應滿足[1 5]：

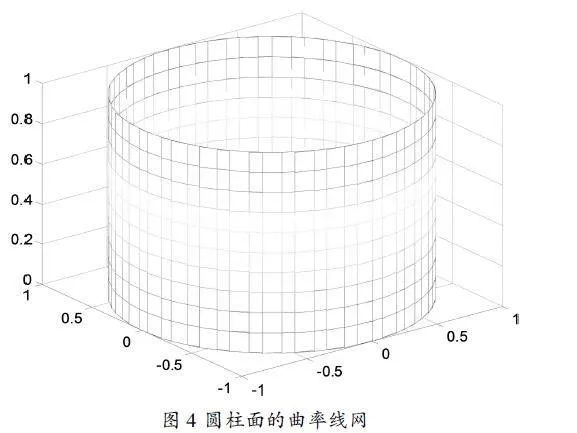
曲面是否都存在曲率線？如果存在的話，如何畫出曲率線？回答這些問題有助于理解曲率線概念。球面上每條曲線都是曲率線；對于圓柱面而言，經計算知道其曲紋坐標網是曲率線網，由水平圓和直母線組成，如圖3.曲率線網常被選為坐標網，因為它具有較好的性質。

3 基本結論直觀教學

3.1 空間曲線一點的鄰近結構

本科的《微分幾何》是局部微分幾何，研究一點處曲線的基本性質。空間曲線在一點鄰近的近似形狀由該點的曲率和撓率完全決定，文獻[14]還給出近似形狀示意圖。例3給出具體實例，說明這一結論。

例3 繪制圓柱螺線及其上點處的Frenet標架，并觀察點處的曲線形狀。

t=-1.5：0.2：2*pi;hold on

plot3（cos（t），sin（t），-t，'r'） ;plot3（1，0，0，'b*'）

[X，Y]=meshgrid（-0.5：0.25：1）; Z=-Y;mesh（X，Y，Z）

x=ones（1，size（t，2））;y=zeros（1，size（t，2））;

plot3（x，t，-t）%繪制圓柱螺線在點（1，0，0）處的切線

plot3（x，t，t）%繪制圓柱螺線在點（1，0，0）處的副法線

plot3（-t，y，y）%繪制圓柱螺線在點（1，0，0）處的主法線

3.2 空間曲面一點的鄰近結構

在曲面論中，研究曲面一點鄰近的結構是重要問題。文獻[14]指出曲面橢圓點的高斯曲率，曲面沿所有方向都朝同一側彎曲；曲面拋物點，除漸近方向外，一切法截線都朝的反向彎曲；當時，曲面點為雙曲點，此點鄰近曲面近似于馬鞍面，此種情形復雜，下面給出例4予以說明。

例4設馬鞍面，繪制該曲面及點處法截線的方向。

程序略，運行結果為如圖4，在區域1曲面向下彎曲，在區域2曲面向上彎曲。

4 研究性教學案例

梅向明，黃敬之著《微分幾何》第五版3.5節“曲面的主方向和曲率線”研究性教學案例如下。

（1）依據教材講解主方向定義、推導主方向滿足的方程；

（2）研究曲面任一點主方向的個數：非臍點處總有兩個主方向，臍點處每一方向都是主方向；

（3）講解主方向判定定理（羅德里格斯定理）及其證明；

（4）研究問題：給定一個主方向，如何尋找與之共軛的另一主方向？提示學生回想（3）中定理證明過程的第二部分；

（5）羅德里格斯定理應用部分：課堂探究兩個問題，題1是對教材第75頁14題條件做修改，如下：

題1：給出曲面上一條曲率線，設上每一點處的主法向量和曲面在該點處的法向量成定角，但不等于，則為平面曲線。

題2：探究教材第75頁14題的逆命題是否成立。特例情形；對球面、圓柱面而言，題2結論是否正確？

課堂學生研究上述問題，原題留為作業。通過這個活動啟發學生多思考問題，學會探究，進一步地深入理解所學的知識。

（6）學生課后思考：通過參數變換后選取曲率線網為曲紋坐標網的意義。提示學生預習3.6節，從中可以找到答案。

5 結論

目前《微分幾何》課程的教學缺乏直觀性、研究性，這妨礙了學生對基本概念、基本思想方法的理解與運用。本文解決《微分幾何》課程教學的直觀性、研究性問題，針對密切面、撓率及曲率線等基本概念、空間曲線和空間曲面在一點的鄰近結構基本結論，利用MATLAB軟件編寫程序，提供幾何圖形；提供了研究性教學案例，較好地有重點地解決了實際教學中的迫切問題。

參考文獻：

[1]王慧. 建筑幾何中的網格與光滑曲面構造[D].大連：大連理工大學，2020.

[2]沈思昀. 基于微分幾何的立體工件表面缺陷檢測方法研究[D].廣州：華南理工大學，2020.

[3]張建洲. 復雜曲面慢刀伺服磨削加工刀具軌跡規劃方法[D].大連：大連理工大學，2022.

[4]M.克萊因.古今數學思想[M].上海：上海科學技術出版社，1988.

[5]楊凡，黃穎，陳云松，等.基于微分幾何反饋線性化的高超聲速飛行器控制系統實現[J].計算機測量與控制，2022，30（12）：125-130.

[6]潘翔宇，胡小敏，劉琨.基于預測命中點的微分幾何制導律[J].電光與控制，2021，28（07）：41-47.

[7]李鋼，唐陶，郭秀月，等.基于微分幾何方法的高維混沌系統間的復合同步控制[J].遼寧師范大學學報（自然科學版），2020，43（02）：174-178.

[8]夏衛政，徐進廷，黃坤，等.基于微分幾何的固定翼無人機過頂跟蹤地面目標制導方法[J].兵工自動化，2018，37（12）：30-33+38.

[9]杜娟，沈思昀，姚靈芝，等.基于微分幾何的柔性電路板圖像區域識別方法[J].計算機集成制造系統，2022，28（01）：132-139.

[10]貢曉靜，鐘誠，華蓓.基于等距變換的聚類挖掘敏感信息保護方法[J].計算機工程，2011，37（19）：122-125.

[11] 彭家貴，陳卿.微分幾何[M].北京：高等教育出版社，2004.