構建“以學為中心”的數學章節復習課新模式

[摘 要] 研究者發現，同學們在章節復習時可以更好地踐行“以學為中心”，進而在師生互動和生生交流中促進每個學生的發展. 文章以“一元二次方程”的章節復習課為例，通過精心備課、問題驅動和充分讓學驅動教學，實現學生學習能力的發展與提高，構建“以學為中心”的數學章節復習課新模式.

[關鍵詞] 章節復習課;以學為中心;一元二次方程

當前，數學課堂教學改革著重強調“以學為中心”，也就是倡導課堂教學需落實學生的主體地位，充分發揮學生的學習能動性，以教與學的和諧統一來促進學生的發展. 數學章節復習課對學生的綜合運用能力要求較高，而學生的認知基礎又參差不齊，對知識的應用也不夠自然. 因此，如何上好一節章節復習課是一線教師需要深度思考的問題. 近年來，筆者在推進“以學為中心”的改革道路上進行了深入研究，對章節復習課的教學模式進行了反復試驗與矯正，取得了一些進展，下面結合“一元二次方程”的章節復習，談談自己的一些經驗和做法.

構建“以學為中心”的一元二次

方程章節復習課的實踐路徑

1. 問題導入，激活思維

問題1：以“用一根長是20厘米的鐵絲去圍一個矩形”為背景編制一個數學問題. （這是一道開放性問題，思維之門一經打開，很快就有學生提出了教師課前的預設問題“求圍成的矩形面積”）

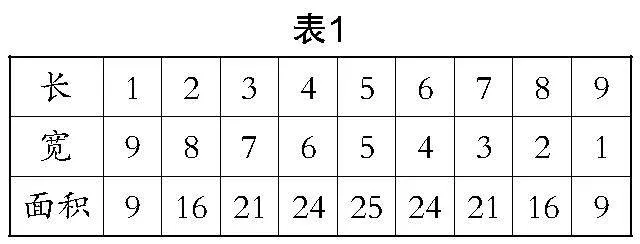
師：我們不妨來探索這個問題！（學生思考后很快有了“答案有多個”的結論，教師立即追問“有多少種可能”. 有學生進一步提出“列表展示”的方法，生成了表1）

生1：不止這些答案，因為長與寬并非只能是整數啊！

師：的確還有其他情況，那還能提出其他關于圍成面積大小的問題嗎？

生2：若圍成的矩形面積是21平方厘米，求矩形的邊長.

生3：那還不簡單，表1中就展示了邊長是7厘米和3厘米的情況.

生4：那可以圍出面積是30平方厘米的矩形嗎？

生5：可以設矩形的一條邊長是x厘米，則另一條邊長是（10-x）厘米，據題意可得x（10-x）=30，就這樣通過設未知數列方程求解.

師：x（10-x）=30屬于哪一類方程，你是根據什么判斷的？（學生又一次展開思考，并通過回憶一元二次方程的定義判斷該方程為一元二次方程）

師（追問）：x（10-x）=30的形式并沒有如定義所述啊？

生6：可以將其轉化為一般式，即x2-10x+30=0.

師：由此可見，整理后轉化為一般式才能判斷該方程是否為一元二次方程. 你能求解此方程嗎？有幾種解法？（這一問題拋出后，學生爭先恐后作答，提出了配方法、直接公式法這兩種解法）

師：一元二次方程有幾種解法？說說每種解法的適用情況. （學生自主展開討論）

生7：事實上，本題并不需要求解，只需要直接計算b2-4ac，由于這里b2-4ac<0，因此本題無解，即無法圍成面積為30平方厘米的矩形. （直到生7解說完，其余學生才恍然大悟）

師：真是思維開闊的孩子，那可以圍出面積是20平方厘米的矩形嗎？（不少學生埋頭計算）

師：剛才大家的探討非常棒！在解決實際問題時，求解后檢驗是否符合題意是必不可少的步驟. 那可以圍出面積是a平方厘米的矩形嗎？（學生又一次陷入沉思，并在思考后得出“此時需要就a值究竟是多少進行討論”的結論）

師（追問）：那什么a值可圍出矩形，什么a值不可以呢？（在思考一段時間后，學生先后給出兩種解決方法：方法一，列出方程并整理，之后根據根的判別式進行判別;方法二，根據配方法求a的取值范圍. 教師對兩種方法均予以高度肯定）

設計意圖 問題的選擇和設計是教學得以成功的關鍵一環. 課始，教師就拋出一個讓學生編題的開放性問題，牢牢抓住了學生的思維與興趣點，為之后課堂的高效推進打下了堅實的基礎. 同時，這一問題在核心概念、原理、知識關聯及思想方法上都體現出典型性，學生在層層推進的探索中可以很好地提煉和內化知識.

2. 拾級而上，深度建構

問題2：現將這根20厘米長的鐵絲一剪為二，分別用這兩段去圍矩形，你能提出一個什么問題？

生9：求這兩個矩形的面積和是多少. 可以是17平方厘米嗎？（問題拋出后，其余學生立刻進入深入思考狀態，并很快解決了問題）

生10：試求圍成兩個矩形的面積和的最大值. （此時，學生已經能踴躍發言，提出“一樣可以用前面的配方法解決問題”）

生11：我改造了題目，把20厘米的鐵絲轉化成了20米的籬笆，然后把這個問題變成了一個雞圈問題. 例如，如圖1，有一段20米長的籬笆，現在靠著一面長是5米的墻圍一個面積是42平方米的雞圈，該如何圍？

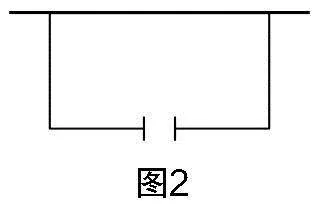
生12：還可以這樣改，如圖2，有一段20米長的籬笆，現在靠著一面長是5米的墻圍一個面積是11平方米的雞圈，并且在前面留出一扇1米長的小門，該如何圍？

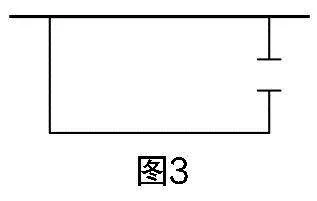
生13：還可以將這扇小門換到圖3所示的位置.

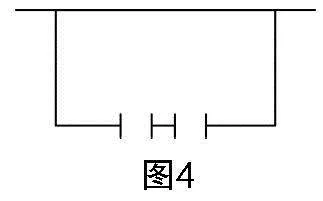
生14：還可以像如圖4這樣圍. （此時，課堂氣氛已經達到了高潮）

師：你們真是一群思維活躍的孩子！下面就讓我們一一解決以上問題……

設計意圖 教師再一次層層遞進地編制問題，并用開放性問題引導學生深入一元二次方程的內核進行探索，使學生在思考、探索、辨析、梳理和總結中建立知識體系，學會靈活運用知識解決問題. 在探索的過程中教師因勢利導，如在編制問題時引導，在學生對問題有困惑時點撥，更多的是充分讓學生在生生互動中建構知識體系，獲得發展.

教學感想

相對于新授課，復習課在實踐“以學為中心”上有著獨特的優勢，這是因為學生對相關知識有了一定認識，盡管學習上存在缺陷，但可以通過復習暴露思維過程，進而在自我剖析和反省中提高認識[1]. 同時，學生學習水平的差異性雖然客觀存在，但合作學習的模式可以精準轉化學困生和優化學優生，進而全面提升數學素養. 為了在章節復習中更好地踐行“以學為中心”，在師生交流和生生互動中促進每個學生的發展，我們可以從以下幾個方面來著手.

1. 通過精心備課改善教師的教

想要上好一節課，精心備課自然是不可或缺的，尤其是想要在章節復習課上出效果，勢必需要教師用心揣摩. 備課時，教師早早定下了在復習課中讓學生自主編題并解答的設想. 讓學生編題并不難，但要引導學生在編題的過程中自然而然地應用所學，達到歸納提煉的效果則是有一定難度的. 當然，教師通過課前的深鉆教材與具體學情，以及課中的因勢利導，使得課堂朝著自己預期的方向發展，且教學也達到了預期效果，尤其是最后幾個學生爭先恐后地提出了具有探究價值的問題讓教師十分欣慰[2]. 顯然，整節課中學生的神采奕奕充分體現了他們取得收獲的喜悅感，這樣的課堂勢必是成功的.

2. 利用創意問題引導學生的學

問題是學生思維的導火索，好的問題可以引領學生思維逐步進階，從而促進深度學習. 本節課的設計巧妙而新穎，拋棄了傳統章節復習課的一貫模式，沒有梳理知識點，也沒有歸納總結，僅僅是用兩個開放性問題貫穿這節課，自主探究、對話交流、思維碰撞，水到渠成地梳理總結章節知識要點、建立知識體系，發展數學核心素養[3].

3. 借助充分讓學促進學生發展

讓學的思想就是將學生置于課堂的主體之中，教師以引導者、啟發者的角色，助力學生的深度思考和探究，讓學生有了更多自主學習、思考和探索的機會與平臺，實現了深度學習. 本課的教學中，教師拋出問題之后千方百計地“讓學”，想方設法地推動“思考”，堅持“以學為中心”，實現章節復習課的質效提升，助力學生核心素養的發展.

參考文獻：

[1]沈良. 試論“知識·探究·思維”路徑下學生核心素養的培養[J]. 數學通報，2017，56（10）：18-22.

[2]沈良. “大概念，大任務”視角下的數學單元教學設計[J]. 中學教研（數學），2021（07）：9-13.

[3]呂世虎，楊婷，吳振英. 數學單元教學設計的內涵、特征以及基本操作步驟[J]. 當代教育與文化，2016，8（04）：41-46.