探索核心素養(yǎng)背景下滲透模型思想的方法

[摘 要] 核心素養(yǎng)背景下的數(shù)學(xué)教學(xué)需關(guān)注模型思想的滲透. 文章以模型思想的概述為起點(diǎn)，分別從定理教學(xué)、試題探索、案例示范三個方面對模型思想的滲透方法展開例析，并從方向明確、方法得當(dāng)、適當(dāng)實(shí)施三個角度談一些思考與感悟.

[關(guān)鍵詞] 模型思想;核心素養(yǎng);定理

有數(shù)學(xué)家認(rèn)為，學(xué)生在學(xué)校所學(xué)的知識到工作中用到的并不多，但學(xué)習(xí)過程中深入內(nèi)心的思維方式、思想方法、數(shù)學(xué)精神、推理能力或研究問題的視角等，卻會長久地發(fā)揮作用，令學(xué)習(xí)者受益終身[1]. 隨著新課改的推進(jìn)，模型思想被列入核心素養(yǎng)的范疇，如何在初中數(shù)學(xué)教學(xué)中滲透模型思想呢？實(shí)踐證明，依靠幾種幾何模型或應(yīng)用題遠(yuǎn)遠(yuǎn)達(dá)不到預(yù)期效果，反而會局限學(xué)生的思維，讓學(xué)生覺得只有提到“模型”或“應(yīng)用”等詞匯才屬于模型思想. 殊不知，模型思想有著更廣泛的定義.

模型思想的概述

模型思想是指有意識地應(yīng)用數(shù)學(xué)原理或方法來理解或解決實(shí)際問題的思想，緊扣客觀對象的本質(zhì)特征，用恰當(dāng)?shù)臄?shù)學(xué)語言進(jìn)行表征的過程. 從狹義的角度來看，模型思想就是解決客觀問題的思想方法，如方程、函數(shù)、不等式等模型就是聯(lián)系數(shù)學(xué)學(xué)科與生活實(shí)際的紐帶. 由廣義的視角來分析，引導(dǎo)學(xué)生用數(shù)學(xué)思維思考并解決實(shí)際問題是模型思想的本質(zhì). 不論是概念教學(xué)，還是用復(fù)雜的知識解決綜合性問題，都是培養(yǎng)模型思想的契機(jī).

值得注意的是模型思想與數(shù)學(xué)建模并不是一回事，模型思想屬于從廣義的角度研究數(shù)學(xué)問題，而數(shù)學(xué)建模則屬于狹義的范疇. 事實(shí)上，核心素養(yǎng)背景下的數(shù)學(xué)教學(xué)，更需從廣義的角度來探索蘊(yùn)含豐富內(nèi)涵的模型思想，這是促使學(xué)生形成關(guān)鍵性人格品質(zhì)的主要途徑.

滲透模型思想的措施

1. 模型思想滲透在定理教學(xué)中

案例 “圓周角定理”的教學(xué)

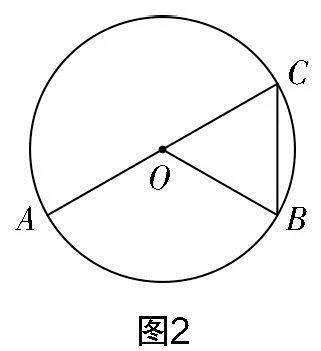
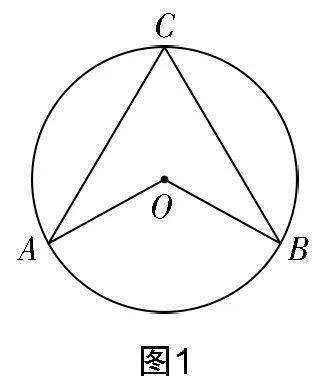
師：如圖1，∠AOB與∠ACB所對的弧為同一條，請分別測量出弧AB所對的兩個角的度數(shù)，分析它們之間存在怎樣的關(guān)系.

生1：測得∠AOB與∠ACB的度數(shù)分別為110°與55°，110°恰好為55°的2倍.

師：這個結(jié)論是否適用于所有情況呢？現(xiàn)在請大家自主畫一個任意圓，并從中取任意一段弧，分析這段弧所對的圓心角與圓周角的度數(shù)關(guān)系.

學(xué)生自主畫圖并測量，很快就獲得結(jié)論：在任意圓中，同一段圓弧所對的圓心角的度數(shù)為圓周角的2倍.

師：為了進(jìn)一步驗(yàn)證該結(jié)論是否正確，現(xiàn)在請大家來看計(jì)算機(jī)的演示：借助幾何畫板以動畫演示的方法分別測量∠AOB與∠ACB的度數(shù)，要求學(xué)生通過觀察分析圓心角與圓周角的度數(shù)關(guān)系.

生2：我發(fā)現(xiàn)不論所取的弧在什么位置，∠AOB始終為∠ACB的2倍.

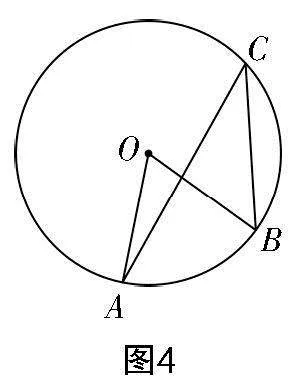
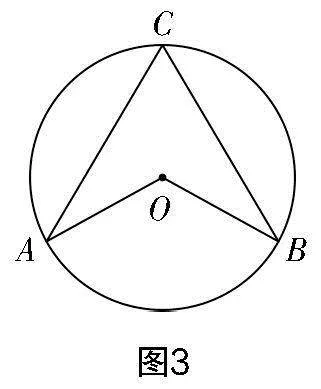
師：通過這個證明，可確定圓心處于圓周角的邊上位置時，猜想是成立的. 那么關(guān)于圖3與圖4的情況，猜想是否依然成立呢. 請以小組合作的方式來探索.

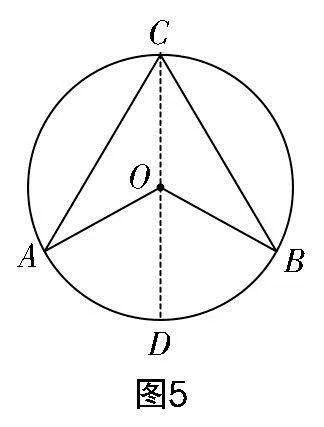
生4：既然我們已經(jīng)探索了圓心處于圓周角邊上的情況，那么借助輔助線CD，可將問題轉(zhuǎn)化成類似于圖2的情況（見圖5），由此可直接獲得∠AOD=2∠ACD與∠BOD=2∠BCD，所以∠AOB=2∠ACB.

師：上述證明方法應(yīng)用了遷移與轉(zhuǎn)化的過程. 還有其他方法嗎？

生5：若在圖4中作CD這條輔助線可得圖6，也就是將圖形轉(zhuǎn)化成了大家所熟悉的圖2，結(jié)論也就浮出水面.

分析 此教學(xué)片段，學(xué)生所提煉到的模型思想為：把圓心處于圓周角的內(nèi)部、外部，轉(zhuǎn)化成圓心處于圓周角的一邊上進(jìn)行探索與研究. 觀察此教學(xué)片段的明線，學(xué)生主要親歷了用數(shù)學(xué)符號語言來描述數(shù)學(xué)問題數(shù)量關(guān)系的過程;基于教學(xué)暗線分析，此環(huán)節(jié)將模型思想貫穿始終，主要體現(xiàn)在“提出問題—建立模型—分析與應(yīng)用”方面.

2. 模型思想滲透在案例示范過程中

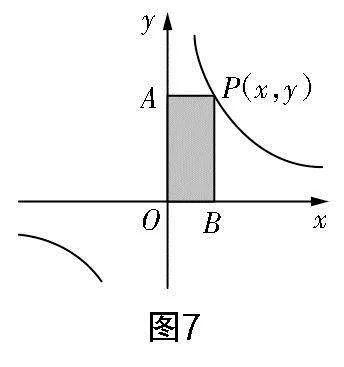
案例2 “反比例函數(shù)”的探索

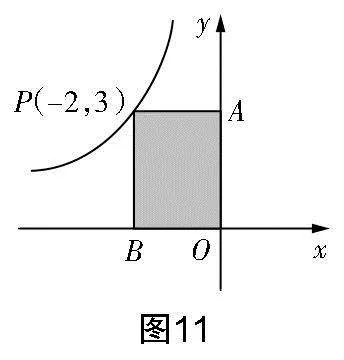
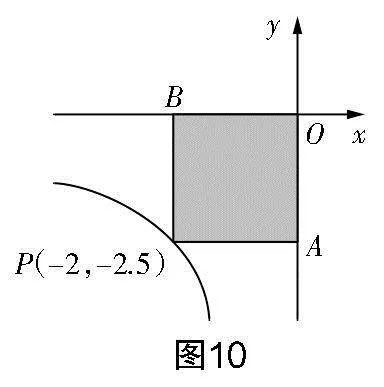
點(diǎn)P（2，2.5），S的值是多少？③如圖10，若點(diǎn)P（-2，-2.5），S的值是多少？

通過對以上問題的探索，根據(jù)相關(guān)因素假設(shè)與分析初步形成模型Ⅰ，即S與k的數(shù)量關(guān)系為______.

通過對以上問題的探索，根據(jù)相關(guān)因素假設(shè)與分析初步形成模型Ⅱ，即S與k的數(shù)量關(guān)系為______.

基于以上結(jié)論，進(jìn)行驗(yàn)證（略）.

模型的應(yīng)用：

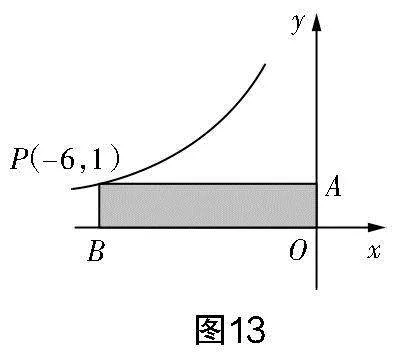
△ABO的面積.

分析 以開門見山的方式展開探索，學(xué)生在問題情境的研究與思考中抽象出基本模型. 其中，問題串的應(yīng)用成功將靜態(tài)的知識動態(tài)化，讓學(xué)生由圖象出發(fā)，對這部分內(nèi)容由感性認(rèn)識逐漸轉(zhuǎn)化為理性認(rèn)識. 循序漸進(jìn)的問題是為提煉模型所設(shè)定的小目標(biāo)，解決問題的過程不僅讓學(xué)生感知了坐標(biāo)與線段長的關(guān)系、S與k的關(guān)系，還促使學(xué)生自主類比、猜想、思考，從而抽象出相應(yīng)的模型，驗(yàn)證與應(yīng)用模型是感性認(rèn)識上升到理性理解的過程，學(xué)生在此過程中提升了模型意識.

關(guān)于滲透模型思想的幾點(diǎn)思考

1. 方向明確

當(dāng)前的數(shù)學(xué)課堂教學(xué)更注重學(xué)生的主體性地位. 教師作為課堂的組織者，需引導(dǎo)學(xué)生親歷實(shí)際問題轉(zhuǎn)化為模型的過程，并鼓勵學(xué)生自主計(jì)算并檢驗(yàn)結(jié)論，為改善教學(xué)方法提供參考依據(jù). 因此，作為具體執(zhí)教的數(shù)學(xué)教師需明確教學(xué)方向，引導(dǎo)學(xué)生在充分理解數(shù)學(xué)的基礎(chǔ)上，為后續(xù)學(xué)習(xí)更多復(fù)雜的內(nèi)容夯實(shí)思維與方法基礎(chǔ).

當(dāng)遇到一個問題時，學(xué)生必須有明確的思考方向，明白哪里是思維的起點(diǎn)，該朝什么方向去分析，通過問題的解決逐步建立學(xué)習(xí)信心. 一旦師生都有明確的“教與學(xué)”的方向，并以積極互動的模式加強(qiáng)探索與分析，必然能有效增強(qiáng)學(xué)生學(xué)習(xí)的主動性，拔高學(xué)生的思維，幫助學(xué)生成功建立模型思想，最終實(shí)現(xiàn)教學(xué)相長.

2. 方法得當(dāng)

數(shù)學(xué)學(xué)習(xí)并不僅僅局限于將實(shí)際生活問題轉(zhuǎn)化為專業(yè)的數(shù)學(xué)問題那么簡單，更重要的是引導(dǎo)學(xué)生學(xué)會用數(shù)學(xué)的眼光觀察現(xiàn)實(shí)世界，用數(shù)學(xué)的思維來思考現(xiàn)實(shí)世界，鼓勵學(xué)生學(xué)會提煉學(xué)習(xí)方法與數(shù)學(xué)思想，讓學(xué)生感知不同模型可以用來解決同一個現(xiàn)實(shí)問題，同時，同一個模型又能用來解決各類不同的現(xiàn)實(shí)問題. 學(xué)生一旦明確了這一點(diǎn)，自然而然地會對數(shù)學(xué)模型產(chǎn)生濃厚的興趣.

為了培養(yǎng)學(xué)生的數(shù)學(xué)模型思想，還可以創(chuàng)設(shè)一些數(shù)學(xué)建模比賽，激發(fā)學(xué)生的潛能，鼓勵學(xué)生在自主探索中提升學(xué)力，以真正發(fā)展學(xué)生的“四基與四能”，提升學(xué)生的“三會”能力，讓核心素養(yǎng)落地生根.

3. 適度實(shí)施

沒有一門學(xué)科是獨(dú)立存在的個體，學(xué)科與學(xué)科之間多多少少有一些聯(lián)系，正是這種關(guān)聯(lián)催生了豐富多彩的世界. 模型思想的滲透同樣需從跨學(xué)科的角度來整合學(xué)生的思維，引發(fā)學(xué)生的合作意識[2]，并通過文獻(xiàn)資料的查閱與信息的收集等，不斷提升學(xué)生的能力.

值得注意的是課堂中滲透數(shù)學(xué)模型思想，需關(guān)注對學(xué)生思維廣泛性、靈活性、容錯性的培養(yǎng)，但初中階段的學(xué)生受認(rèn)知水平的限制，在這一方面還有所欠缺，而學(xué)生的時間又是有限的，因此教師要杜絕將模型思想的滲透等同于建模活動要求，因?yàn)閷W(xué)生提出過高要求反而會消減學(xué)生學(xué)習(xí)的積極性，得不償失. 事實(shí)證明，根據(jù)學(xué)生的實(shí)際認(rèn)知發(fā)展水平適度滲透模型思想是拔高學(xué)生數(shù)學(xué)思維，激發(fā)學(xué)生創(chuàng)新意識的重要舉措.

參考文獻(xiàn)：

[1]邵光華. 作為教育任務(wù)的數(shù)學(xué)思想與方法[M]. 上海：上海教育出版社，2009.

[2]曹培英. 數(shù)學(xué)基本思想與學(xué)科核心素養(yǎng)[J]. 教育研究與評論（中學(xué)教育教學(xué)版），2016 （10）：91-92.