蛇形管道機器人設計與軌跡跟蹤算法實現

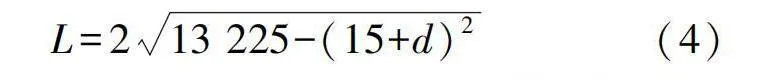
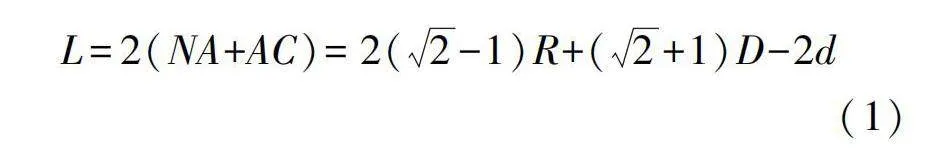
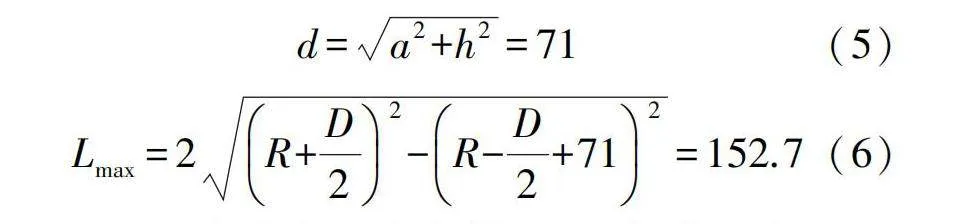
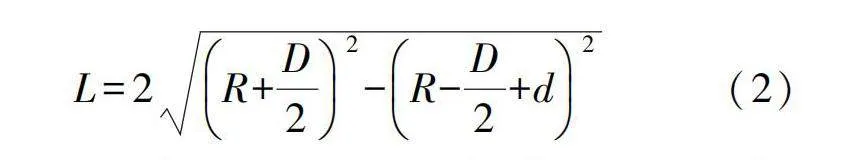
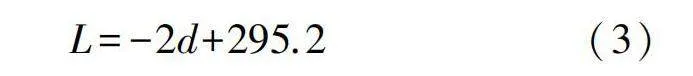
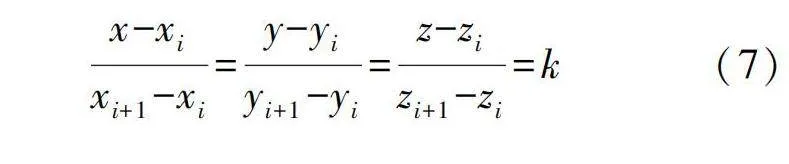
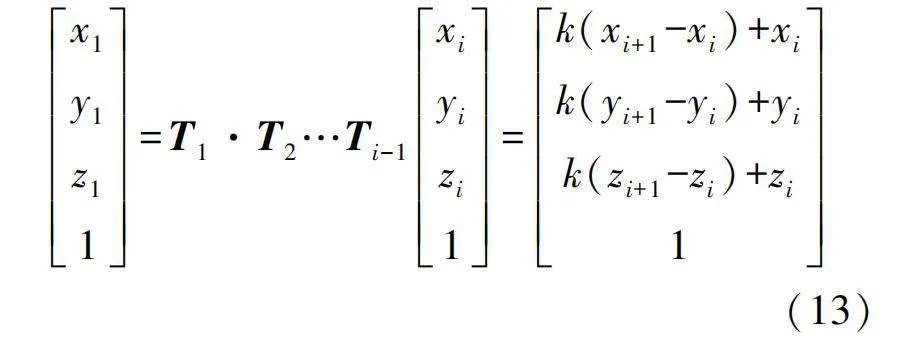
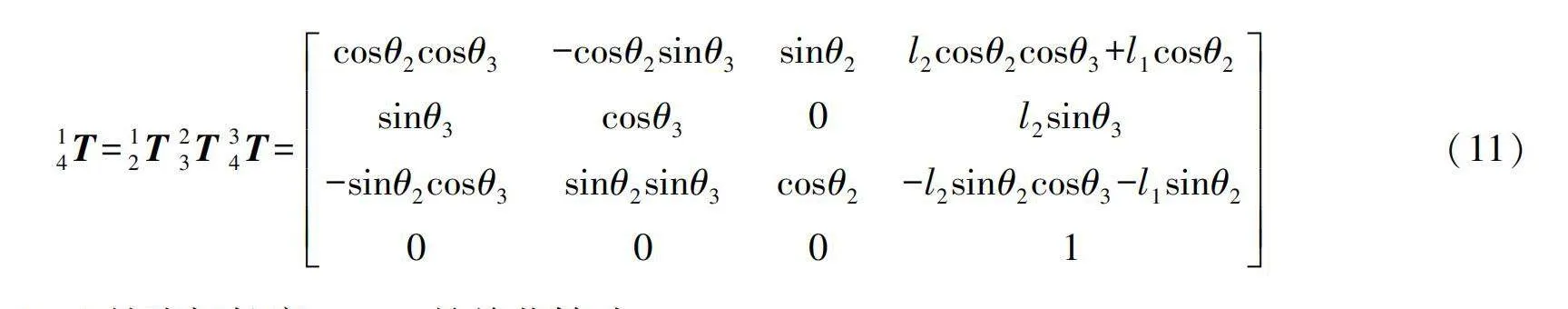
摘 要：蛇形機器人模仿蛇的身體結構與運動機理，具有體積小、自由度多等特點，在復雜環境中表現出優秀的運動性能。設計一種適用于狹小管道環境的蛇形機器人，采用模塊化的構型，機器人共擁有5個自由度。利用Denavit-Hartenberg方法對機器人進行運動學分析，基于從機器人尾部到頭部的前向軌跡跟蹤控制算法，建立機器人的軌跡跟蹤運動控制方法；設計實驗樣機并開展運動控制實驗和實際管道轉彎實驗，驗證了機器人結構設計的合理性、逆運動學的正確性和運動控制方法的有效性。

關鍵詞：蛇形機器人；軌跡跟蹤；運動學；管道環境應用

中圖分類號：TP242 文獻標志碼：B 文章編號：1671-5276（2024）04-0201-07

Design of Snake Robot in Pipeline and Implementation of Trajectory Tracking Algorithm

YU Yangguang， JI Aihong， QIU Jiahui， LIU Yahong， QIN Guodong

（College of Mechanical and Electrical Engineering， Nanjing University of Aeronautics and Astronautics， Nanjing 210016， China）

Abstract：Snake robot， imitating the body structure and motion mechanism of snake， small in size and multiple with degrees of freedom， displays excellent motion performance in complex environment. A snake robot suitable for narrow pipe environment was proposed. With modular configuration， the proposed robot had 5 degrees of freedom， and kinematics analysis was conducted by Denavit-Hartenberg method. Based on the forward trajectory tracking control algorithm from the tail to the head of the robot， the trajectory tracking motion control method of the robot was established. The experimental prototype was designed and the experiments on motion control and actual pipe turning were carried out， which verified the rationality of the robot structure design， the correctness of the inverse kinematics and the effectiveness of the motion control method.

Keywords：snake robot; trajectory tracking; kinematics; pipeline application

0 引言

自然界中，蛇具有優異的運動能力，這取決于其獨特的身體結構與運動方式。蛇有130～500個脊椎骨，每兩節脊椎骨通過一個球窩結構連接在一起，雖然兩個脊椎骨之間繞垂直軸的相對旋轉運動為10°～20°，繞水平軸的相對旋轉運動僅有幾度，但蛇的靈活性正是由這些脊椎骨的微小運動總和而產生^[1]。這種機械式的互聯為仿生蛇形機器人帶來了設計靈感。

蛇形機器人^[2]以蛇類脊柱為模仿對象，相鄰關節間可以彎曲一定角度，通常由若干相同的模塊通過多自由度的關節串聯而成^[3]。因其具有體積小、運動靈活、環境適應性強等特點，被廣泛應用于設備維護、災害救援等領域。蛇形機器人在結構上可分為三類：帶有從動輪的蛇形機器人、不帶從動輪的蛇形機器人和配備有主動推進裝置的蛇形機器人。前兩類無主動推進裝置的蛇形機器人，需要像真正的蛇一樣在橫向波動中移動，依靠自身扭動產生的驅動力進行運動，限制多，速度慢。相比之下，具有主動推進裝置的蛇形機器人可以在每個節段中產生推進力，即使在沒有橫向波動的情況下也能移動。

由于自由度較多，蛇形機器人的控制方法比較復雜。常用的運動控制方法主要有基于蛇形曲線的控制方法、基于數學模型的控制方法和基于CPG（central pattern generators）的控制方法等^[4-5]。基于蛇形曲線的控制方法運算簡便，但不利于傳感信息的引入；基于數學模型的控制方法可以實現對蛇形機器人的精確控制，但建模過程比較復雜；基于CPG的控制方法，可以在缺乏高層調節和外部反饋的情況下自動產生穩定的振蕩行為，但僅適用于機器人的節律性運動控制。

針對蛇形機器人的運動控制，OWEN^[6]基于大量的生物蛇實驗推導出了蜿蜒運動軌跡曲線（Serpenoid曲線）用于蛇形機器人的運動控制。ARIIZUMI等^[7]基于蛇形機器人運動有側滑約束條件建立了蛇形機器人的運動學模型，基于該運動學模型在機器人頭部額外添加一個剛性連桿，用于控制蛇形機器人的運動方向。LILJEB?CK等^[8]提出應用虛設的機構VSOP（virtual structure for orientation and position）將蛇形機器人等效為機械臂進行建模研究。CHO等^[9]提出頂尖隨動算法，直接控制機器人的頭部單元，后續的主體單元跟蹤頭部單元的運動。這種后級單元的運動跟隨前級變化的移位控制方法在其他機器人上也有應用^[10]，但此方法根據機器人頭部的運動來確定后級各單元的運動，很難直接改變機器人頭部以外部分的運動。唐超權等^[11]利用Cohen神經元模型，為蛇形機器人的運動控制設計了多模態中樞模式發生器模型，用來產生機器人運動的多種步態信號。

蛇形機器人優秀的運動靈活性與環境適應性，賦予了其應用于狹小管道環境的可能。在電力、化工等行業存在大量管徑狹小、環境復雜的管道，此類管道在極端環境下易于損壞，需要機器人在管道內部執行檢測、維修等操作^[12]。為了滿足狹小管道環境對蛇形機器人尺寸和運動能力的實際需求，本文提出了一種適用于管道內部的蛇形機器人，采用機器人關節與行進機構配合的構型，保證了復雜環境下機器人的運動能力；采用從機器人尾部到頭部的前向軌跡跟蹤算法，實現了機器人的軌跡跟蹤運動控制，并搭建機器人樣機完成實驗，驗證了機器人結構設計的合理性和運動控制方法的有效性。

1 蛇形機器人

1.1 結構設計

狹小管道環境需要特種機器人具備小型化、輕量化、多自由度的特點以及靈活的運動能力。針對直徑在80mm～100mm的厘米級管道，本文提出了一種蛇形機器人構型以適用于狹小管道環境下的運動和相關任務執行。設計需求歸納如下：

1）具備主動運動能力，運動靈活性高，便于控制；

2）結構尺寸小，管徑適應性強，對管徑尺寸要求小；

3）對彎管、T型管等復雜管道環境適應性強；

4）可搭載圖像采集傳輸模塊等執行器，滿足管道內檢測需求。

機器人整體方案設計對機器人的運動性能起決定作用，主要包括運動方式、驅動方式和關節連接方式等。綜合分析設計需求與不同運動方式的機器人，本文選取的機器人形式為配備有主動驅動裝置的蛇形機器人，機器人為多關節結構，相鄰關節間可以彎曲一定角度，擁有更多的自由度，更有利于機器人在狹小管道內的靈活運動。電機直接驅動執行機構的方式占用空間小，有利于降低機器人整體尺寸，故機器人主動推進裝置選擇為直流電機直接驅動的主動輪結構，輪式結構運動速度快，結構簡單，同時保證了較大的驅動力。機器人關節連接方式選擇為正交連接，該連接方式具有可靠性高、結構工藝性好、控制簡單等優點，機器人各關節采用舵機直接驅動的形式，實現俯仰或偏轉自由度。

根據上述整體設計方案，蛇形機器人采用三模塊的結構（圖1（a）），單個模塊如圖1（b）所示，包含機器人關節和行進機構兩部分。機器人關節與行進機構配合的構型可以使機器人兼具較多的自由度和較高的運動速度。機器人關節由兩個呈正交布置的伺服電機組成，類似于“十字結構”，具備偏轉、俯仰兩個自由度，能在水平或垂直平面內轉動，轉動角度范圍為（-90°，90°）。行進機構包括直流電機、支架與主動輪。支架兩端伸出懸臂用于連接關節部分。

1.2 彎管通過性設計

機器人的尺寸是決定其在管道內通過性的最關鍵因素，在設計中應根據管道形狀及尺寸判斷機器人的尺寸設計區間以保證機器人的通過性。

直管對機器人的尺寸要求較低，機器人寬和高不超過管道內徑即可。

彎管對機器人的尺寸要求較高，機器人能否順利通過彎管主要由管道曲率及機器人尺寸決定。彎管主要參數如下：曲率半徑R、管道內徑D、直角彎管彎曲角度γ=90°。機器人不具備彎管通過性一般是由于機器人過于細長或過于短粗兩種情況造成的，極端位置處于彎管中機器人傾斜45°處。

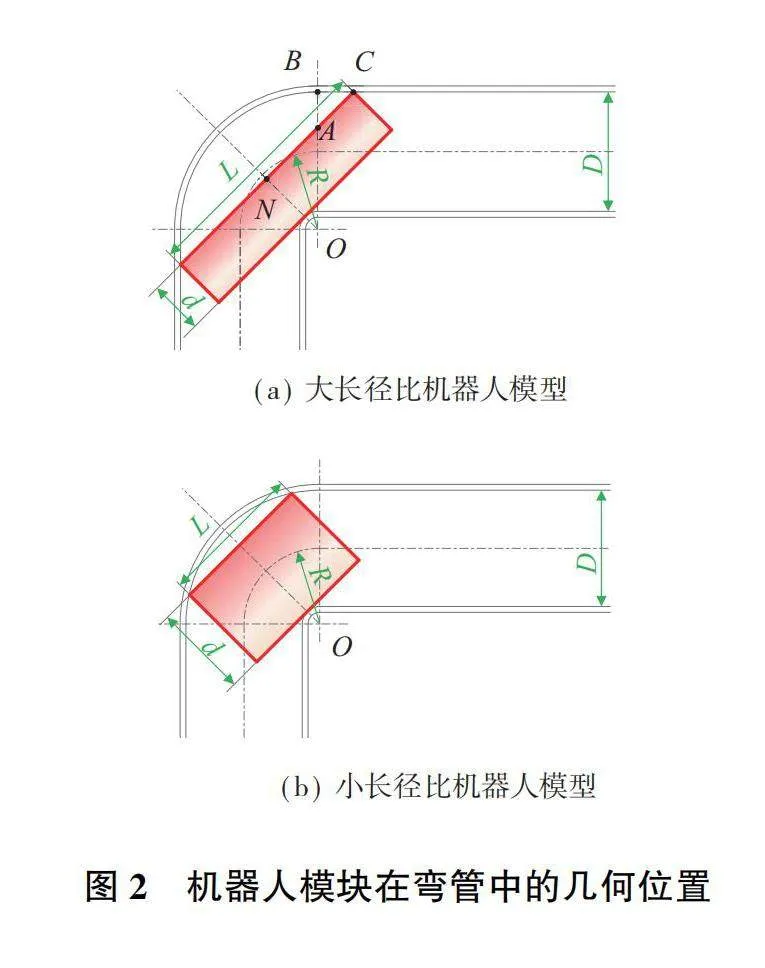
將彎管建模為如圖2所示的圓柱形管段，機器人單個模塊簡化為圓柱形結構，長度為L，直徑為d。根據圖2可以求出管道內徑、曲率半徑和機器人尺寸之間的關系。

當機器人過于細長，即機器人簡化模型的長徑比L/d較大時，機器人前后端面位于管道的直邊部分。機器人與彎管的尺寸滿足0lt;d≤（R+D/2）sin45°－（R－D/2），此時通過幾何關系計算機器人長度和直徑的關系如下：

當機器人過于短粗，即機器人簡化模型的長徑比L/d較小時，機器人前后端面位于管道彎曲部分。機器人與彎管的尺寸滿足（R+D/2）sin45°－（R－D/2）lt;d≤D，此時機器人長度和直徑的關系如下：

本文所設計機器人針對的管道尺寸參數為：R=65mm，D=100mm。在此彎管環境下，機器人為保證通過性應滿足以下條件。

當機器人簡化模型的直徑滿足0lt;d≤66.3mm時，長度計算公式如下：

當滿足66.3mmlt;d≤100mm時，長度計算公式如下：

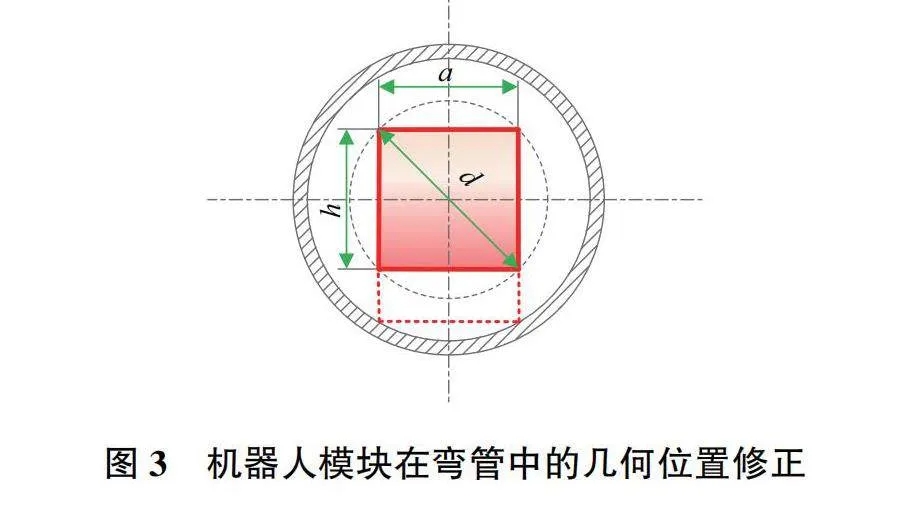
前文將機器人模型簡化為圓柱形結構，實際中機器人結構多樣，不局限于圓柱形結構。如果機器人為矩形體結構，那么機器人中心所處平面不位于管道軸心平面，即機器人未必與管道同軸。另外機器人運動卡死時還可能發生跳動，造成機器人所處平面的改變以擴大運動空間通過管道。本文在機器人設計中對其尺寸進行了更強的約束，若機器人為矩形體結構，其寬高構成的斜邊尺寸應小于圓柱形結構的直徑d，如圖3所示。

本文設計機器人單個模塊的長寬高分別為L=115mm，a=50mm，h=50mm，代入公式計算如下：

機器人在寬高已定的情況下，模塊的長度可取范圍為（0，152.7）。設計中L=115mm，故機器人的尺寸設計在彎管通過性方面是合理的。

2 運動控制方法

2.1 軌跡跟蹤算法

軌跡跟蹤是蛇形機器人進入狹窄工作空間的常用方法之一，其目的是控制機器人各個關節的轉動角度、角速度等變量使機器人能對一條給定的軌跡進行跟蹤。機器人軌跡跟蹤算法的關鍵是以一定的方式不斷更新多關節機器人的空間位置，不能將移動機器人整體視作一個點，也不能只關注機器人頭部位置的擬合，而是要對機器人整體進行每個關節的軌跡跟蹤。具有主動推進裝置的蛇形機器人通常采用移位控制，根據機器人頭部的移動或運動學來確定后級各單元的運動，很難直接改變機器人頭部以外部分的運動。而傳統的蛇形臂等超冗余度機器人采用的軌跡跟蹤過程主要有兩種：一種為已知機器人末端關節的位置或姿態，然后根據給定軌跡反向求解其余關節的關節變量，完成逆運動學求解；另一種為驅動箱進給運動，正向依次擬合各個關節到給定軌跡上求解關節變量，完成逆運動學求解。受此啟發，本文針對所設計的蛇形機器人，將機器人各關節以一定速度沿連桿切向方向進給，從機器人尾部開始，依次將每個關節擬合到跟蹤曲線，使機器人的軌跡跟蹤簡化為各機器人連桿末端對任務曲線離散點的連續跟蹤擬合的過程，最終求解關節變量以完成逆運動學求解。

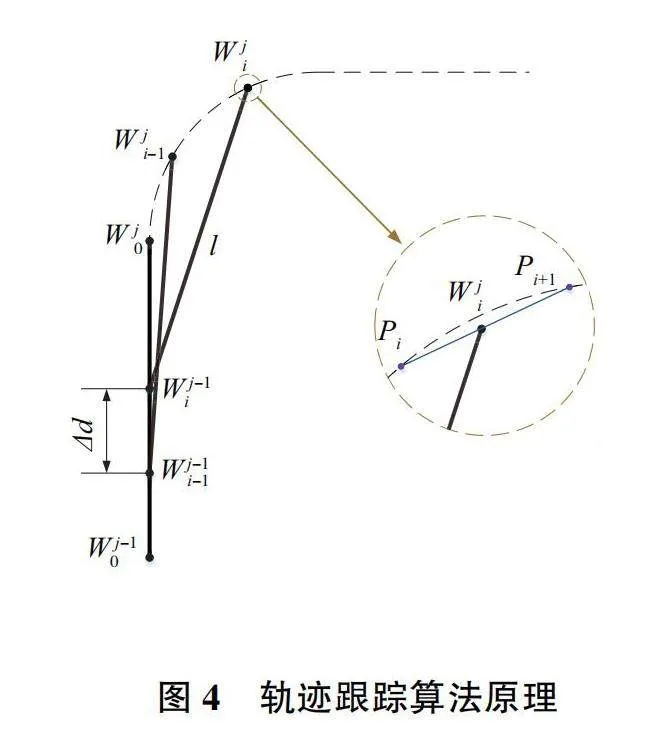
本文采用跟蹤算法的原理如圖4所示。圖中粗線部分表示機器人的一個簡化連桿，初始時刻連桿首尾兩端位置為W^j－1₀，W^j₀，機器人以一定速度運動。假設連桿的首尾兩端在t時刻移動到W^j－1_i－1，W^j_i－1處，在下一時刻t+Δt時，連桿尾端更新至W^j－1_i位置。通過桿長l可以確定連桿首端W^j_i的位置區間，連桿的位置更新為W^j－1_i，W^j_i。

如圖4中的局部放大圖所示，連桿首端W ^j_i移動至離散曲線上P_i和P_i+1的工作區域中，在極限小距離內曲線可以近似由直線代替，通過兩點確定一條直線，可以獲得在P_i（x_i，y_i，z_i）和P_i+1（x_i+1，y_i+1，z_i+1）處的線性方程：

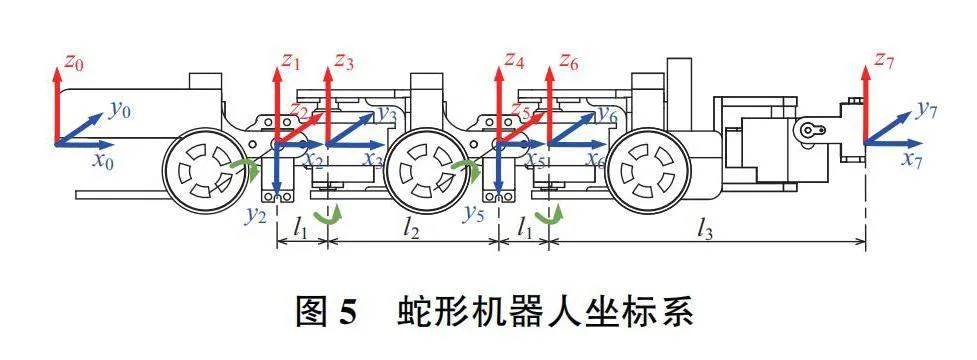
W^j_i在基坐標系中的位置坐標可以通過機器人的正運動學方程獲得。本文設計的蛇形機器人每個相鄰關節的運動方向均保持正交，且機器人為多模塊結構，相鄰模塊間的坐標變換規律相同。本文利用D-H分析法（denavit-hartenberg method）^[13]，完成機器人的運動學建模，建立如圖5所示的坐標系，D-H參數如表1所示。

蛇形機器人相鄰模塊之間的齊次變換矩陣相同，以其中一個模塊為例，從坐標系{4}到坐標系{1}的齊次變換矩陣為：

式中：l_i（i=1，2，3）是連桿長度；θ₂、θ₃是關節轉動角度。

可以得到相鄰模塊之間的齊次變換矩陣，基于此機器人各模塊的位姿通過逐次變換也可以準確地描述出來。

通過線性方程和機器人的運動學方程，聯立式（7）、式（12）可以得到：

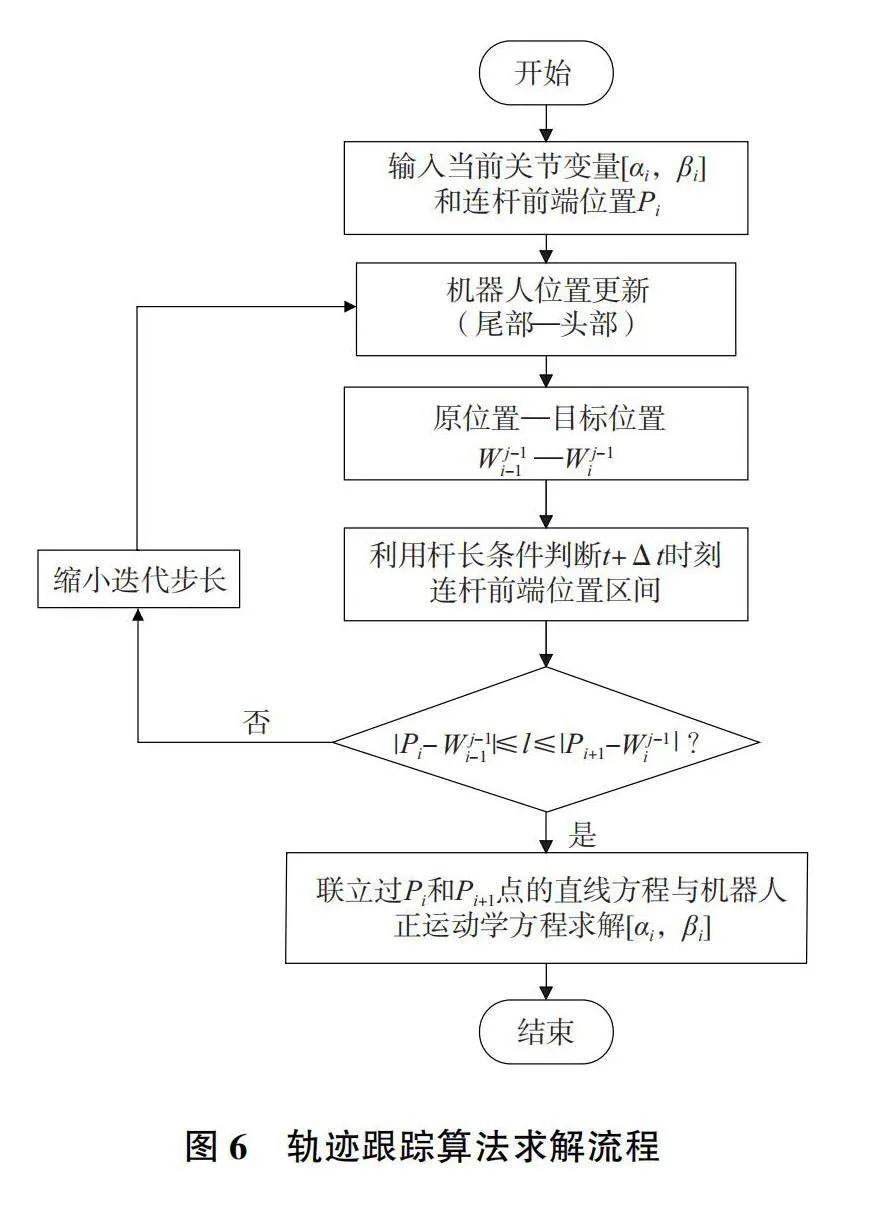
該方程包含3個未知量α_i，β_i，k，存在唯一的解，即蛇形機器人的逆運動學解。蛇形機器人的軌跡跟蹤就是通過聯立過P_i，P_i+1的直線方程和機器人的正運動學方程，得到逆運動學解α_i，β_i和相應的坐標位置x_i，y_i，z_i來完成。軌跡跟蹤算法求解流程如圖6所示。

2.2 仿真實驗

本文首先通過仿真驗證了軌跡跟蹤算法的有效性，針對機器人實際應用的管道環境存在彎管，在x-y平面設計了轉彎曲線作為目標軌跡，曲線參數的設定取決于實際彎管的尺寸參數。

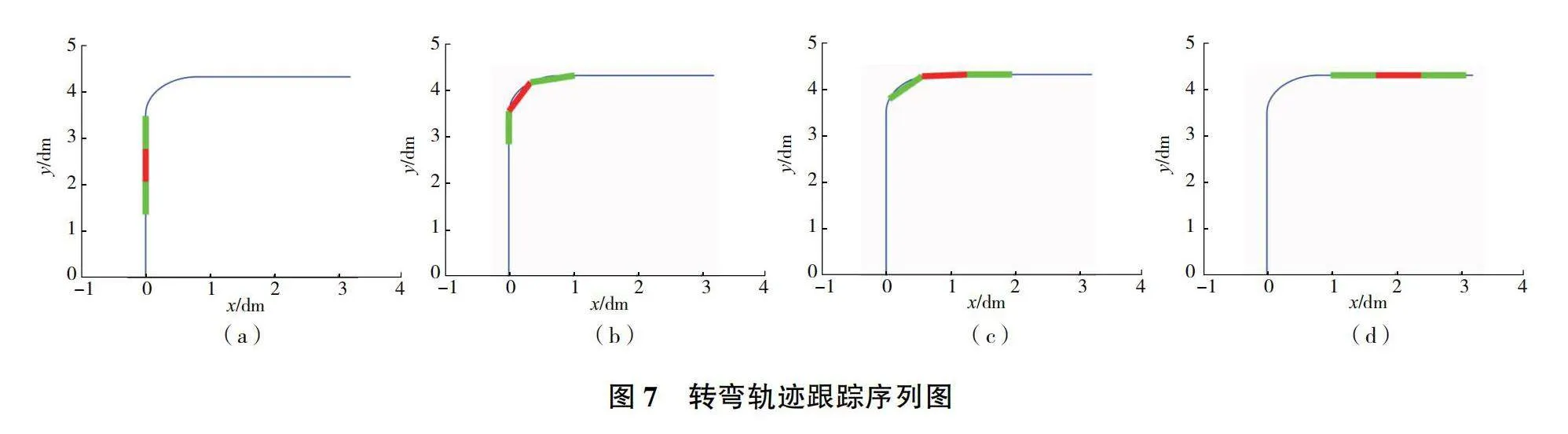
仿真中的蛇形機器人結構如圖1所示，擁有3個模塊，5個自由度。機器人設置為以恒定速度50mm/s移動。采用軌跡跟蹤算法對機器人的每個關節求解運動學逆解，得到仿真結果。機器人轉彎軌跡跟蹤仿真的序列圖如圖7所示。從圖中可以看出機器人各關節在跟蹤目標曲線時具有很好的擬合度，逆運動學求解正確，在整個跟蹤過程中，機器人運動平穩、位置偏移較小。

轉彎曲線僅需機器人在二維平面進行軌跡跟蹤，不涉及三維空間運動，所以機器人俯仰關節的旋轉角度α_i總是0，只有偏轉關節的旋轉角度β_i需要進行計算，結果如圖8所示。從圖中可以看出，關節轉角在整個跟蹤過程中，由初始時刻的0 rad轉變為-5π/18 rad，再以相反的趨勢轉變為0 rad。整個過程中轉角變化十分平穩，關節逆運動學解無奇異，并且每個時刻的關節旋轉角度均處于關節轉角的變化范圍（-π/2，π/2）之內，跟蹤任務可以在設計的極限旋轉角度內完成。

3 樣機實驗

3.1 實驗設計

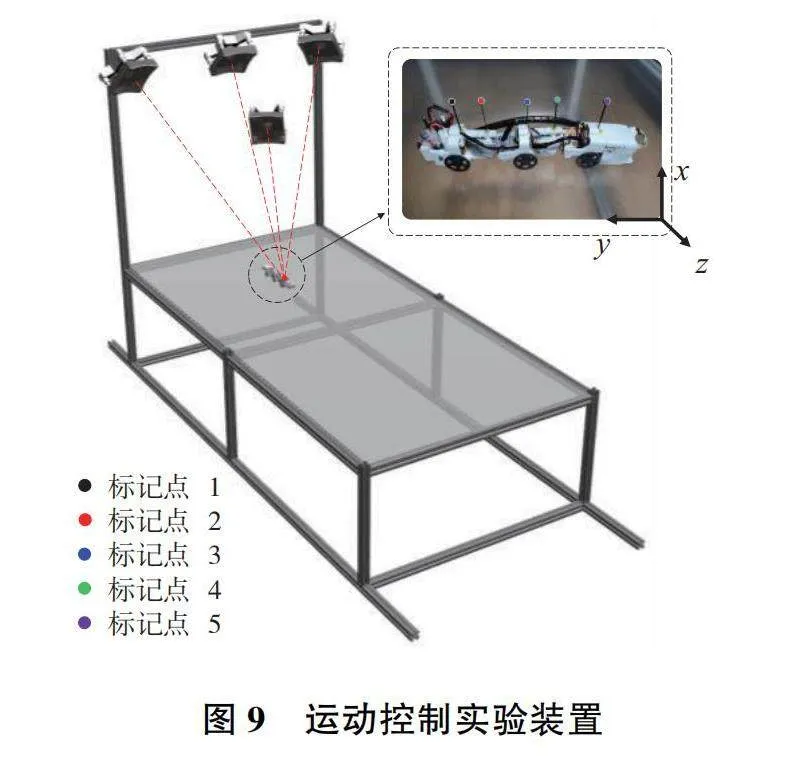
蛇形機器人樣機的長寬高尺寸為310mm×50mm×50mm，機器人連接件、支架和主動輪由高性能樹脂材料通過3D打印技術制作而成。該機器人配備4個伺服電機（KST DS215MG），3個直流電機（CHW-GW12T-N20VA），主動輪外緣覆蓋有橡膠圈用于增加摩擦力。實際測得機器人的直線運動速度為50mm/s，機器人總質量為300g，各零部件之間通過螺栓螺母連接。機器人上安裝有5個熒光標記點，以便于后期機器人關鍵點的捕捉與運動分析，標記點分別位于機器人每一模塊的關節部分和行進機構部分，具體位置如圖9中放大圖所示（本刊黑白印刷，相關疑問咨詢作者）。蛇形機器人置于如圖9所示長1 800mm，寬860mm的水平實驗平臺上。實驗平臺周圍安裝有4臺高速攝像機，從4個不同的視角拍攝機器人的運動實驗，用來確定標記點在整個空間區域的三維坐標信息。實驗中選擇與軌跡跟蹤仿真中相同的目標曲線，利用算法求解出的關節轉角對機器人進行控制。針對目標曲線的軌跡跟蹤運動，共進行了10次實驗。在高速攝像機獲取運動序列后，運行程序跟蹤所設置的5個熒光標記點，然后利用直接線性變換DLT方法（direct linear transformation）獲得任意時刻下這些標記點的坐標數據^[14]。

3.2 實驗結果

完成運動控制實驗后，將10次實驗中各標記點的坐標數據求取平均值并進行線下擬合，得到機器人各標記點的運動軌跡。圖10顯示了蛇形機器人進行轉彎運動的實驗結果。

在整個運動過程中，蛇形機器人按照目標軌跡進行軌跡跟蹤，與目標軌跡保持了較好的擬合度，這與理論模型非常吻合。在運動過程的某些階段，機器人標記點軌跡與目標曲線存在一定誤差。5個標記點最大距離誤差的平均值為12mm，誤差百分比為2.8%。這些實驗結果較好地驗證了機器人運動學分析與軌跡跟蹤算法的正確性。

為了進一步驗證機器人在管道環境下的運動性能，本文開展了實際管道內的轉彎實驗。管道參數如下：入口直徑80mm，90°直角轉彎至直徑100mm的管道。實驗結果如圖11所示，可以觀察出機器人能適應此類狹小管道環境，完成管道內的轉彎運動。

通過對機器人的運動控制實驗和實際管道內的轉彎實驗，得出結論：蛇形機器人的結構設計具備合理性，針對機器人設計的軌跡跟蹤算法具備有效性，并且機器人在管道環境下進行了實際測試，運動性能滿足使用要求。

4 結語

1）基于蛇的身體結構所帶來的仿生設計靈感，結合狹小管道應用場景，設計了三模塊五自由度蛇形機器人。機器人多關節與行進機構配合的構型，保證了蛇形機器人的多自由度，提高了機器人對管道環境的適應性。

2）對蛇形機器人進行了運動學分析，基于從機器人尾部到頭部的前向軌跡跟蹤控制算法，實現了蛇形機器人的軌跡跟蹤運動控制。仿真結果表明：機器人軌跡跟蹤偏移量較小，逆運動學求解的關節角度變化滿足連續性與平穩性，可以實現機器人各關節精確跟蹤目標軌跡的控制需求。

3）搭建了蛇形機器人樣機，設計并開展了運動控制實驗和實際管道環境下的轉彎實驗。實驗結果表明：機器人軌跡跟蹤精度較高，運動平穩，在實際管道環境下可以實現直角轉彎，進一步驗證了機器人設計的合理性、逆運動學的正確性和運動控制方法的有效性。未來將著重于解決機器人運動中存在的滑動問題，通過結構優化和誤差補償等方式彌補由滑動帶來的誤差。今后，準備探索將該機器人應用于豎直管道的可能性。

參考文獻：

[1] （挪）帕爾·李列巴克（Pal Liljeback），等. 蛇形機器人：建模、機電設計及控制[M]. 譚天樂，譯. 北京：國防工業出版社，2015：5-14.

[2] MANZOOR S， CHOI Y. A unified neural oscillator model for various rhythmic locomotions of snake-like robot[J]. Neurocomputing，2016，173：1112-1123.

[3] 張月， 董雷， 宦榮華，等. 風電葉片管道內窺履帶機器人的設計與運動分析[J]. 中國機械工程， 2021， 32（15）：1884-1889.

[4] 龍艷琴. 變剛度二維蛇形機器人機構設計與運動控制研究[D]. 南京：東南大學，2021.

[5] 唐超權， 馬書根， 李斌，等. 具有環境適應能力的蛇形機器人仿生控制方法[J]. 中國科學（信息科學）， 2014， 44（5）：647-663.

[6] OWEN T. Biologically inspired robots：snake-like locomotors and manipulators[J]. Robotica，1994，12（3）：282.

[7] ARIIZUMI R，TANAKA M，MATSUNO F. Analysis and heading control of continuum planar snake robot based on kinematics and a general solution thereof[J]. Advanced Robotics，2016，30（5）：301-314.

[8] LILJEB?CK P，STAVDAHL ?，PETTERSEN K Y. Modular pneumatic snake robot 3d modelling，implementation and control[J]. IFAC Proceedings Volumes，2005，38（1）：19-24.

[9] CHO C N，JUNG H，SON J，et al. An intuitive control algorithm for a snake-like natural orifice transluminal endoscopic surgery platform：a preliminary simulation study[J]. Biomedical Engineering Letters，2016，6（1）：39-46.

[10] TANAKA M，NAKAJIMA M，TANAKA K. Smooth control of an articulated mobile robot with switching constraints[J]. Advanced Robotics，2016，30（1）：29-40.

[11] 唐超權， 馬書根， 李斌，等. 基于神經步進激勵機制的蛇形機器人環境自適應仿生控制策略[J]. 機械工程學報， 2013，49（1）：53-62.

[12] 邢利輝， 王亞慧， 鄧蕊. 管道探測蛇形機器人控制系統設計及仿真[J]. 小型微型計算機系統， 2020， 41（6）：1340-1344.

[13] DENAVIT J，HARTENBERG R S. A kinematic notation for lower-pair mechanisms based on matrices[J]. Journal of Applied Mechanics，1955，22（2）：215-221.

[14] DIANE H， THERIAULT， NATHAN W， et al. A protocol and calibration method for accurate multi-camera field videography[J]. Journal of Experimental Biology， 2014， 217：1843-1848.

收稿日期：2023-01-06